Turing Machines At last Designing Universal Computational Devices

Turing Machines (At last!)

Designing Universal Computational Devices Was Not The Only Contribution from Alan Turing… Enter the year 1940: • The world is at war • Nazi Germany has succeeded in conquering most of west Europe • Britain is under siege • British supply lines are threaten by German • Germany used the Enigma Code, considered unbreakable • Alan Turing led a group of scientist that broke the enigma code Enter the year 2006: The National Security Agency (NSA) needs people! (www. nsa. gov)

Background • Automata accepts regular languages only For example, {anbn : n = 0, 1, …} is not regular • Pushdown Automata accepts context-free languages only For example, {anbncn : w *} is not context-free • We can easily write an algorithm (in C) recognizing if a sequence of characters have the form anbncn or not

The Key Question • Is it possible to design a formal model of a computational device that capture the capabilities of any algorithm? Alan Turing, 1940’s: Yes!

Basic Idea Turing decomposed operations in the device as follows: • A pencil will be “observing” symbols from a paper • The pencil can move left and right • Computational steps erase a symbol observed by the pencil and write a new one in its place • The decision about which symbol should be written and which will be observed next depend on: 1. The current symbol being observed 2. The “state of mind” of the device This device is called a Turing Machine

Turing Machine Looks Similar to Finite Automata Common: • A “state of mind” sounds like the collection of states • A “pencil” sounds like the pointer for the next word Main differences: • Turing machines can write on the “paper” • Turing machines can backup and read symbols again This turns out to be a major difference!

In Turing’s Own Words . . . which can be made to do the work of any special-purpose machine, that is to say to carry out any piece of computing, if a tape bearing suitable "instructions" is inserted into it.

Expressivity of Turing Machines (TMs) • TMs can simulate any data structure • TMs can simulate major components of imperative languages: sequence, branching and loop • TMs can control branching and loops • Several extensions have been attempted: adding multiple heads (pencils), tapes, non-determinism, etc. But we can show that TMs can simulate each of these extensions

Church-Turing Thesis Every computer algorithm can be implemented as a Turing machine Therefore, C, C++, Prolog, Lisp, Small talk, and Java programs can be simulated in Turing machines Definition: a programming language is Turing-complete if it is equivalent to a Turing machine.

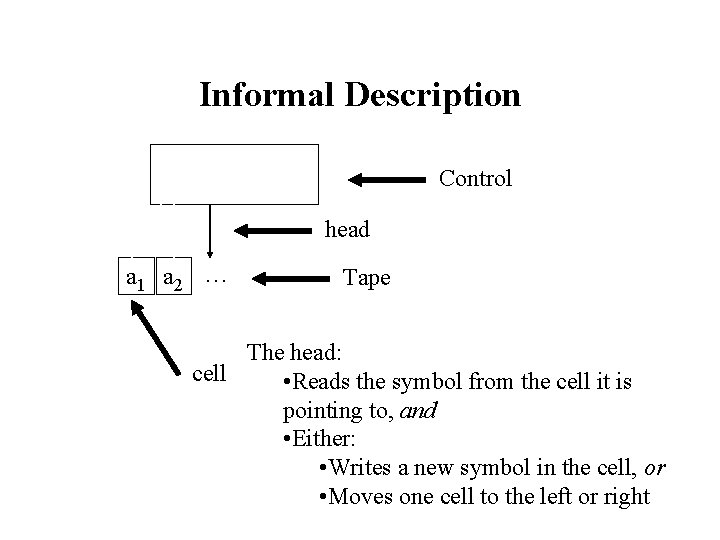
Informal Description Control head a 1 a 2 … Tape The head: cell • Reads the symbol from the cell it is pointing to, and • Either: • Writes a new symbol in the cell, or • Moves one cell to the left or right

Informal Description (II) • New cells can be added to the right of the tape as needed (similar to RAM memory) • These new cells contain the blank symbol, � • The tape is bounded to the left

Preliminaries to Formal Description • denotes the alphabet of characters in language as usual. • denotes the set of symbols that can be written on tape • It contains � and all symbols in • Transitions can be described by (Case I): ((s, a), (q, b, )) If the machine is in state s and the current cell has an a then jump to state q and write b in the current cell and moves head to right

Preliminaries to Formal Description (II) • Transitions can be described by (Case II): ((s, a), (q, b, )) If the machine is in state s and the current cell has an a then jump to state q and write b in the current cell and moves head to left

Formal Definition. A Turing machine is a 7 -tuple (Q, , q 0, qaccept, qreject), where: • Q is a set of states • is a set of symbols (the alphabet) • is a set of symbols that can be written in tape, � and • q 0 Q is the initial state • qaccept is the accepting state • qreject is the rejecting state, qreject qaccept

Formal Definition (II) • is a collection of transitions defined by the function: : (Q {qaccept, qreject }) Q { , }

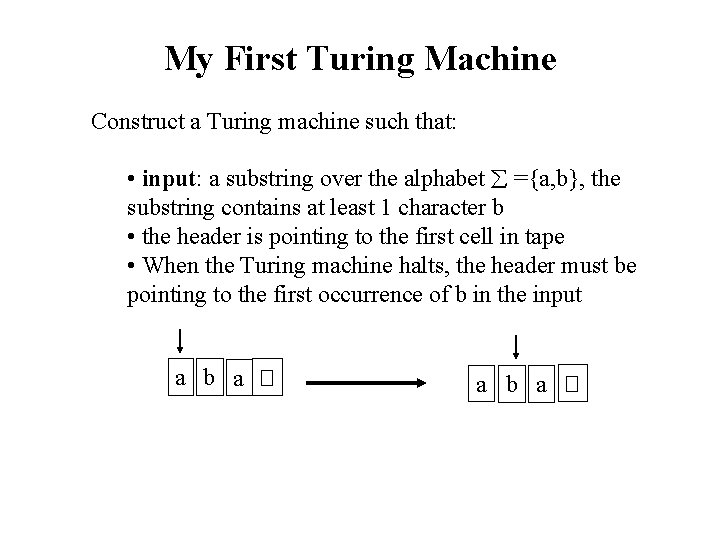
My First Turing Machine Construct a Turing machine such that: • input: a substring over the alphabet ={a, b}, the substring contains at least 1 character b • the header is pointing to the first cell in tape • When the Turing machine halts, the header must be pointing to the first occurrence of b in the input a b a �

Discussion: Are you sure that such a simple model can simulate my C++ program for computing the Minimum Spanning Tree ?

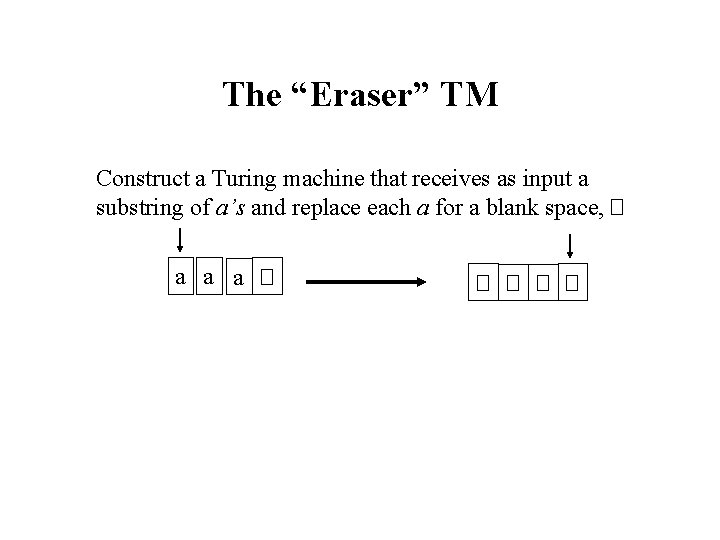
The “Eraser” TM Construct a Turing machine that receives as input a substring of a’s and replace each a for a blank space, � a a a � � �

Configuration for Turing Machines Configuration: (q, h, LS, RS) • The current state, q • The symbol pointed by the head, h • The string left of the head, LS • The string right of the head, RS

Configuration for Turing Machines (2) Instead of writing: (q, h, LS, RS), we write: LSqh. RS If q = qaccept, then LSqh. RS is called an accepting configuration If q = qreject, then LSqh. RS is called a rejecting configuration Examples: - Initial configuration with 3 a’s for the eraser TM: eq 0 aaa� - Accepting configuration starting with eq 0 aaa: ���qaccept�

Computation in Turing Machines • A configuration C 1 = LS 1 q 1 h 1 RS 1 yields a configuration C 2 = LS 2 h 2 q 2 RS 2 in one step, written C 1 C 2, if: There is a transition: (q 1, h 1) = (q 2, h 2, ) • The other case is analogous for (q 1, h 1) = (q 2, h 2, ) * C’: C yields C’, written C There is a sequence of configurations in one step: … • Example: eq 0 aaa yields e���q 0� C 1 C 0 C C’

Two Forms of Computability • Definition. A word w is accepted by a Turing machine M if M yields an accepting configuration starting from the configuration eq 0 w • Definition. The language L(M) recognized by a Turing machine M: L(M) = {w | w accepted by M} • Definition. A language L is Turing-recognizable if there is a Turing machine that recognizes L • Definition. A language L is decidable if there is a Turing machine M such that: ØL(M) = L ØFor any word w L, M yields a rejecting configuration starting from the configuration eq 0 w

Constructing Complex Turing Machines Idea: Use a modular approach similar to the one use to construct complex programs Example (programming): Given two n n matrixes A and B to compute ABT we: 1. Construct a procedure to compute BT, transverse(B, C) 2. Construct a procedure to multiply two matrices, multiply(B, C, D) 3. Call transverse(B, C) and then multiply(A, C, D). D contains the answer

Graphical Conventions We will use a convention similar to a flow chart to indicate how to put together Turing machines (TMs). Convention. Let A and B be 2 TMs, and a be a character in then: A; a A B if a then B Means that: 1. If A halts in a configuration of the form w 1 qacceptaw 2 where w 1 or w 2 are any words 2. Then B starts with the configuration w 1 q 0 aw 2

Graphical Conventions (2) M a A a B M; If a then A else B Means that: • • If M halts in a configuration of the form w 1 qacceptaw 2, then A starts with the configuration w 1 q 0 aw 2 If M halts in a configuration of the form w 1 qaccept w 2 with a, then B starts with the configuration w 1 q 0 w 2

Graphical Conventions (3) a A a while (not a) do A Means that: • If the initial configuration has the form w 1 q 0 w 2, then A starts with this configuration if a, where s is the initial state in A • If A halts in a configuration of the form w 1 qaccept w 2 with a, then A starts with the configuration w 1 q 0 w 2

Basic Turing Machines a Denotes “write a on the current cell” (a is a character in ) Denotes “move to the right of the current cell” (the book uses “R” instead of “ ”) Denotes “move to the left of the current cell” (the book uses “L” instead of “ ”)

Other Simple Turing Machines Machine a � b a What it does “if current cell has an a, then replace it with a b” “if current cell has a character a different than �, then move once to the right and write that a”

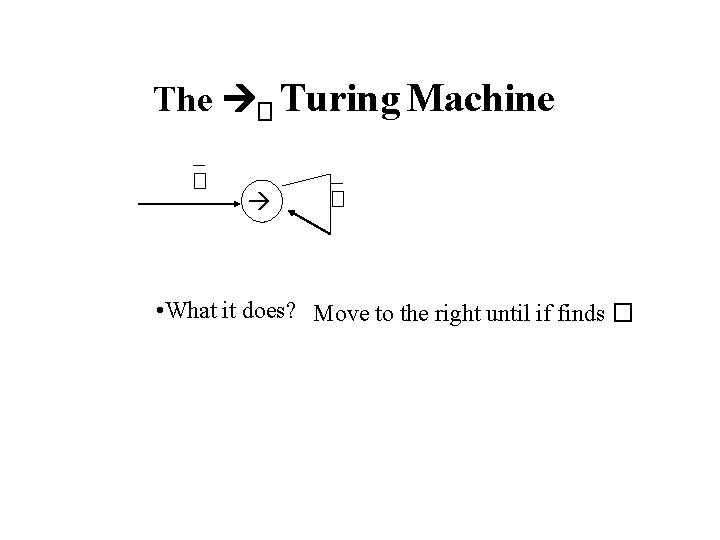
The � Turing Machine – � • What it does? Move to the right until if finds �

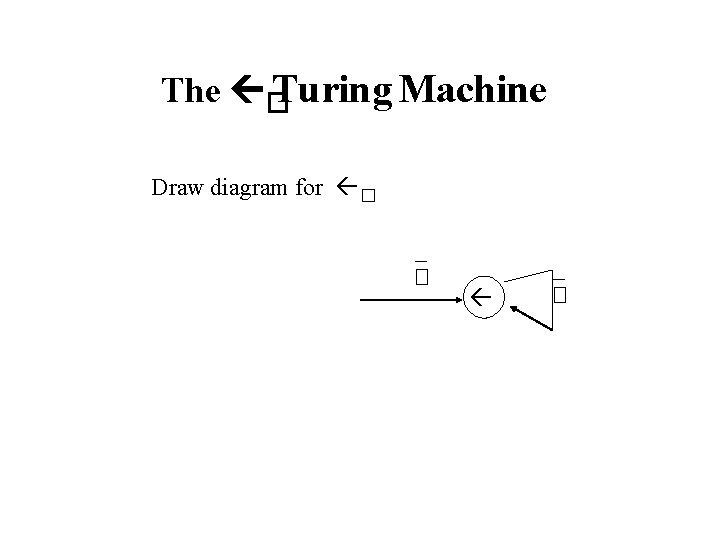
The � Turing Machine Draw diagram for � – �

–� and –� – Move to the left until the first non-blank space cell � is found – � Move to the right until the first non-blank space cell is found

The Conventions • 2 simple rules: • Rule # 1: R “move to the right until you find “ R “move to the right until you find a symbol other than “ Note: first check. Then move (think of a “while”) • Rule # 2: “Never forget Rule # 1” (Mr Miogi, The Karate Kid)

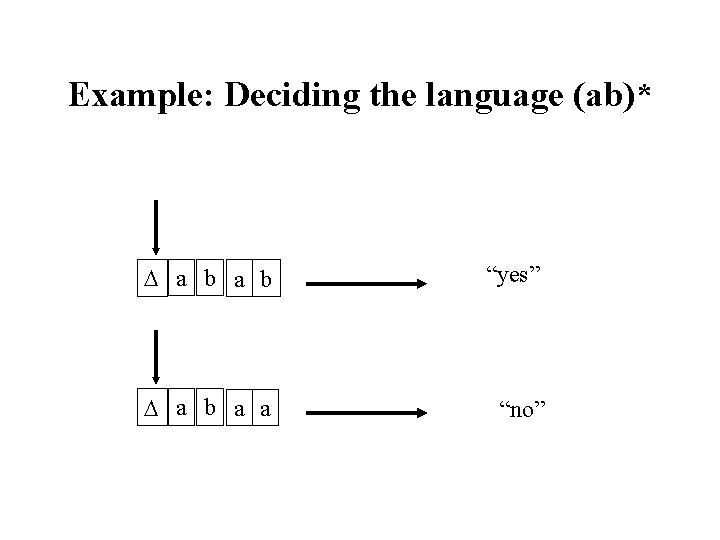
Example: Deciding the language (ab)* a b “yes” a b a a “no”