Turing Machine Turing machine was invented in 1936

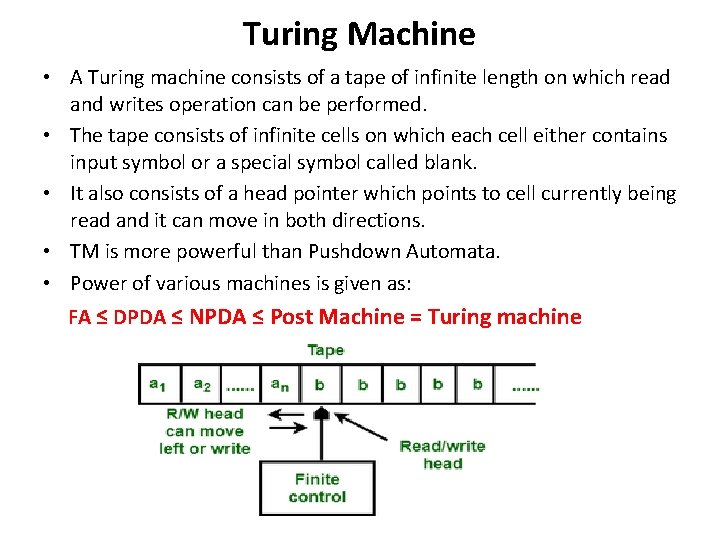
Turing Machine • Turing machine was invented in 1936 by Alan Turing. It is an accepting device which accepts Recursive Enumerable Language generated by type 0 grammar. • There are various features of the Turing machine: • It has an external memory which remembers arbitrary long sequence of input. • It has unlimited memory capability. • The model has a facility by which the input at left or right on the tape can be read easily. • The machine can produce a certain output based on its input. Sometimes it may be required that the same input has to be used to generate the output. So in this machine, the distinction between input and output has been removed. Thus a common set of alphabets can be used for the Turing machine.

Turing Machine • A Turing machine consists of a tape of infinite length on which read and writes operation can be performed. • The tape consists of infinite cells on which each cell either contains input symbol or a special symbol called blank. • It also consists of a head pointer which points to cell currently being read and it can move in both directions. • TM is more powerful than Pushdown Automata. • Power of various machines is given as: FA ≤ DPDA ≤ NPDA ≤ Post Machine = Turing machine

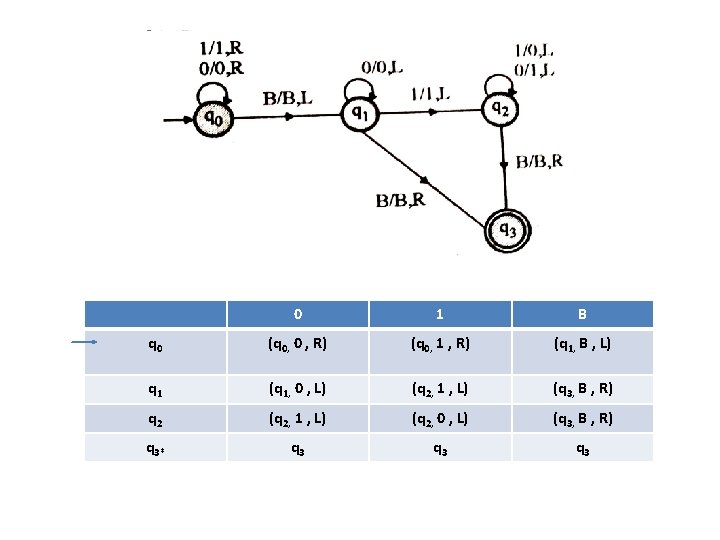
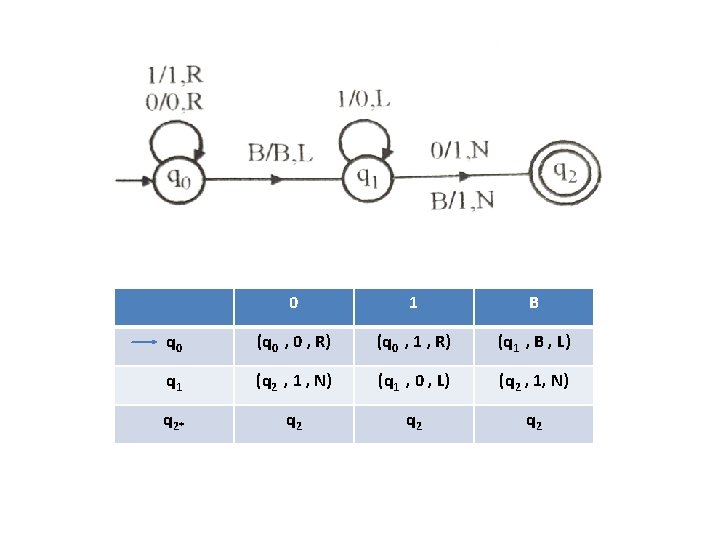
Formal definition of Turing machine • A Turing machine can be defined as a collection of 7 components: Q: the finite set of states ∑: the finite set of input symbols Γ : the tape symbol q 0: the initial state F: a set of final states B: a blank symbol used as a end marker for input δ: a transition or mapping function. • The mapping function shows the mapping from states of finite automata and input symbol on the tape to the next states, external symbols and the direction for moving the tape head. This is known as a triple or a program for Turing machine. • (q 0, a) → (q 1, A, R) • That means in q 0 state, if we read symbol 'a' then it will go to state q 1, replaced a by X and move ahead right(R stands for right).

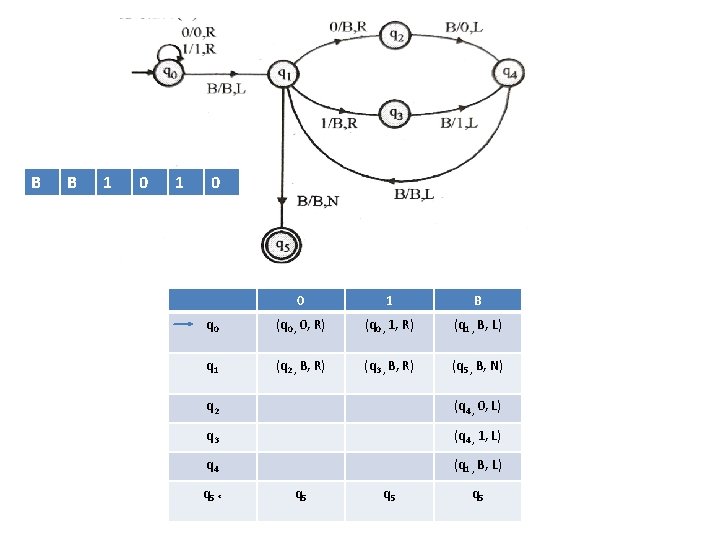
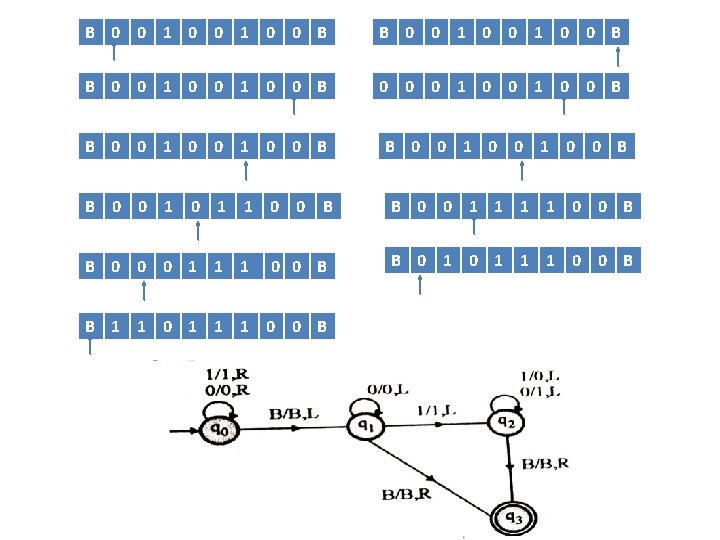
Example Construct TM for the language L ={0 n 1 n} where n>=1. Solution: • We have already solved this problem by PDA. In PDA, we have a stack to remember the previous symbol. The main advantage of the Turing machine is we have a tape head which can be moved forward or backward, and the input tape can be scanned. • The simple logic which we will apply is read out each '0' mark it by A and then move ahead along with the input tape and find out 1 convert it to B. Now, repeat this process for all a's and b's. • Now we will see how this turing machine work for 0011.

• The simulation for 0011 can be shown as below: • Now, we will see how this Turing machine will works for 0011. Initially, state is q 0 and head points to 0 as: • The move will be δ(q 0, 0) = δ(q 1, A, R) which means it will go to state q 1, replaced 0 by A and head will move to the right as: • The move will be δ(q 1, 0) = δ(q 1, 0, R) which means it will not change any symbol, remain in the same state and move to the right as:

• The move will be δ(q 1, 1) = δ(q 2, B, L) which means it will go to state q 2, replaced 1 by B and head will move to left as: • Now move will be δ(q 2, 0) = δ(q 2, 0, L) which means it will not change any symbol, remain in the same state and move to left as: • The move will be δ(q 2, A) = δ(q 0, A, R), it means will go to state q 0, replaced A by A and head will move to the right as: • The move will be δ(q 0, 0) = δ(q 1, A, R) which means it will go to state q 1, replaced 0 by A, and head will move to right as:

• The move will be δ(q 1, B) = δ(q 1, B, R) which means it will not change any symbol, remain in the same state and move to right as: • The move will be δ(q 1, 1) = δ(q 2, B, L) which means it will go to state q 2, replaced 1 by B and head will move to left as: • The move δ(q 2, B) = (q 2, B, L) which means it will not change any symbol, remain in the same state and move to left as: • Now immediately before B is A that means all the 0? s are market by A. So we will move right to ensure that no 1 is present. The move will be δ(q 2, A) = (q 0, A, R) which means it will go to state q 0, will not change any symbol, and move to right as:

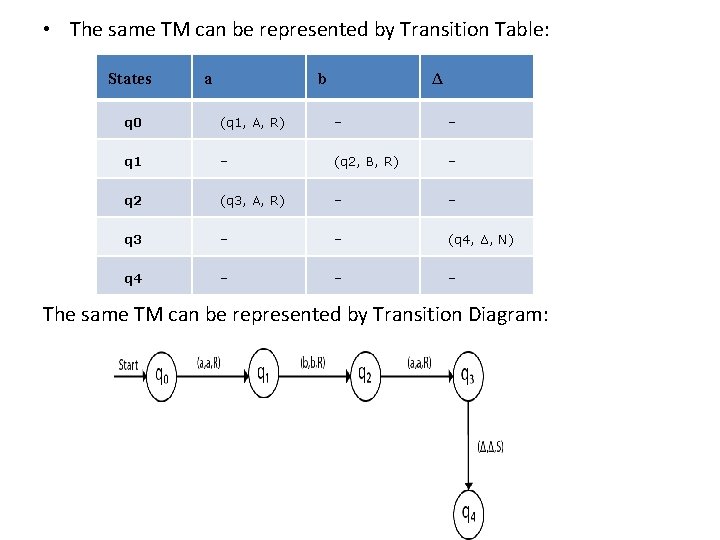
• The move δ(q 0, B) = (q 3, B, R) which means it will go to state q 3, will not change any symbol, and move to right as: • The move δ(q 3, B) = (q 3, B, R) which means it will not change any symbol, remain in the same state and move to right as: • The move δ(q 3, Δ) = (q 4, Δ, R) which means it will go to state q 4 which is the HALT state and HALT state is always an accept state for any TM. • The same TM can be represented by Transition Diagram:

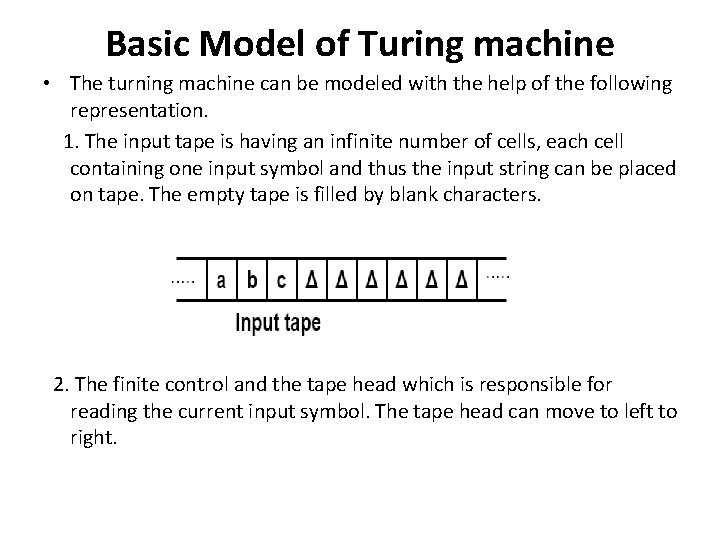
Basic Model of Turing machine • The turning machine can be modeled with the help of the following representation. 1. The input tape is having an infinite number of cells, each cell containing one input symbol and thus the input string can be placed on tape. The empty tape is filled by blank characters. 2. The finite control and the tape head which is responsible for reading the current input symbol. The tape head can move to left to right.

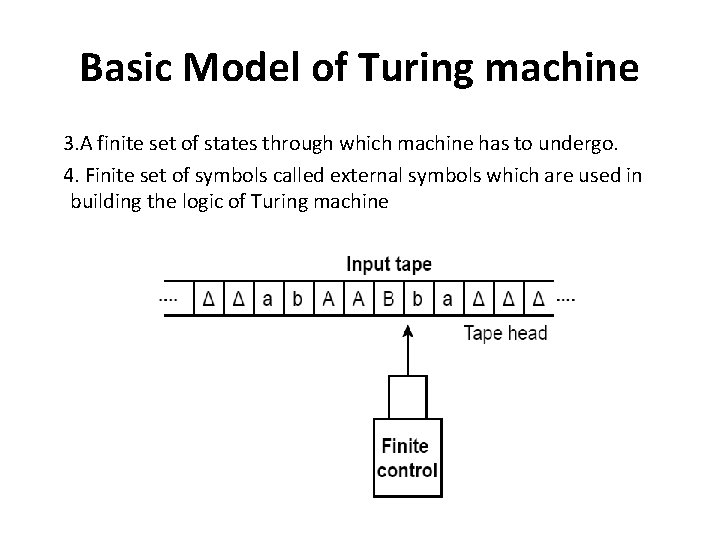
Basic Model of Turing machine 3. A finite set of states through which machine has to undergo. 4. Finite set of symbols called external symbols which are used in building the logic of Turing machine

Language accepted by Turing machine • The Turing machine accepts all the language even though they are recursively enumerable. • Recursive means repeating the same set of rules for any number of times and enumerable means a list of elements. • The TM also accepts the computable functions, such as addition, multiplication, subtraction, division, power function, and many more.

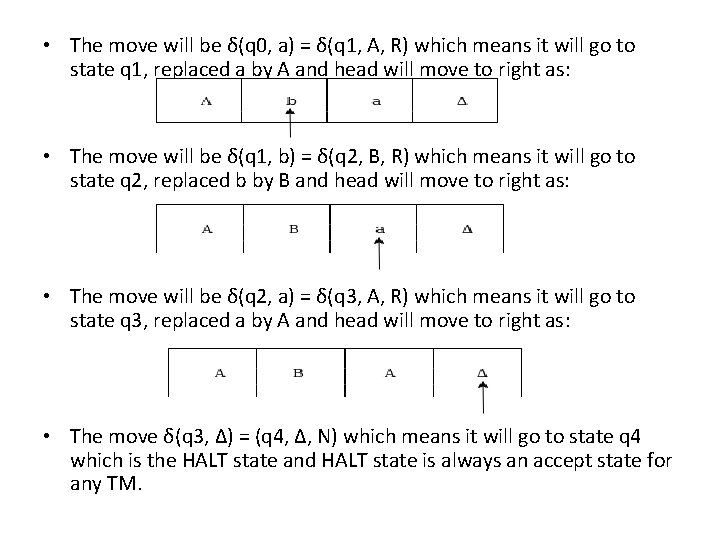
Example Construct a Turing machine which accepts the language of aba over ∑ = {a, b}. Solution: • We will assume that on input tape the string 'aba' is placed like this: • The tape head will read out the sequence up to the Δ characters. If the tape head is readout 'aba' string then TM will halt after reading Δ. • Now, we will see how this Turing machine will work for aba. Initially, state is q 0 and head points to a as:

• The move will be δ(q 0, a) = δ(q 1, A, R) which means it will go to state q 1, replaced a by A and head will move to right as: • The move will be δ(q 1, b) = δ(q 2, B, R) which means it will go to state q 2, replaced b by B and head will move to right as: • The move will be δ(q 2, a) = δ(q 3, A, R) which means it will go to state q 3, replaced a by A and head will move to right as: • The move δ(q 3, Δ) = (q 4, Δ, N) which means it will go to state q 4 which is the HALT state and HALT state is always an accept state for any TM.

• The same TM can be represented by Transition Table: States a b Δ q 0 (q 1, A, R) – – q 1 – (q 2, B, R) – q 2 (q 3, A, R) – – q 3 – – (q 4, Δ, N) q 4 – – – The same TM can be represented by Transition Diagram:

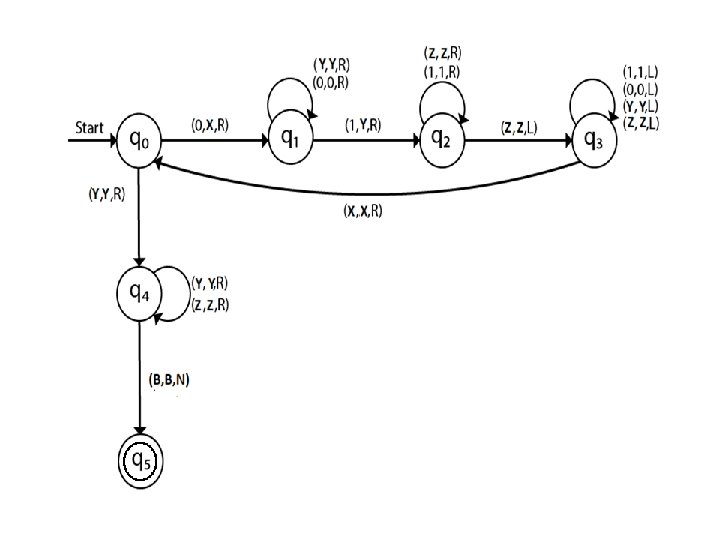
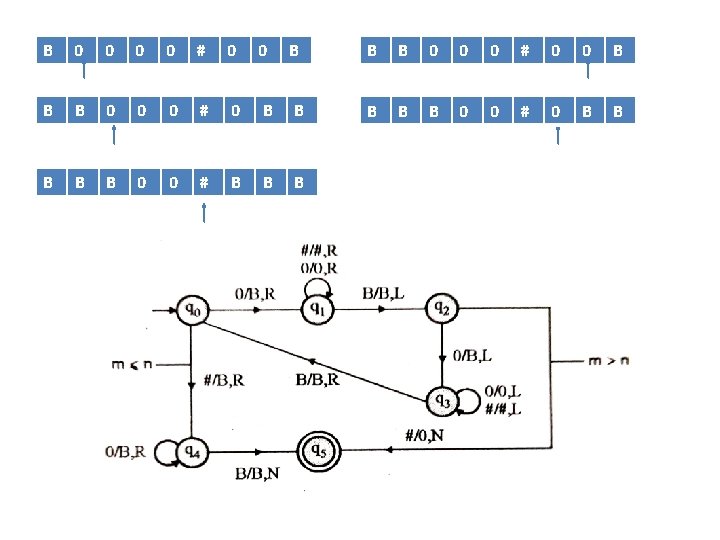
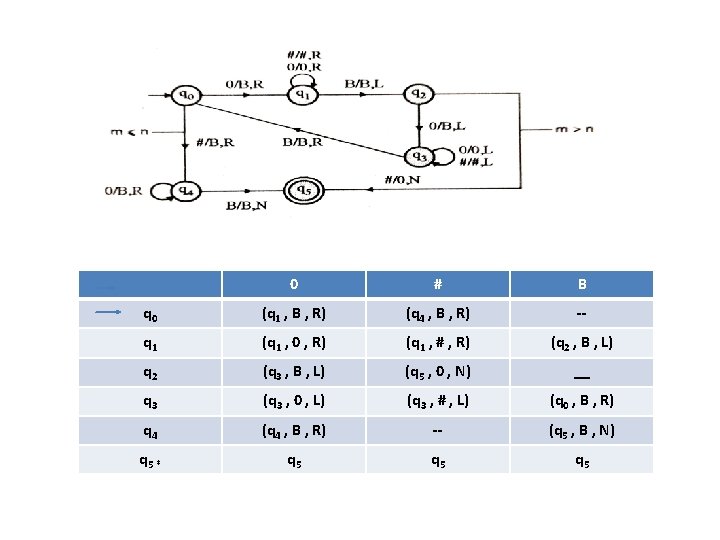
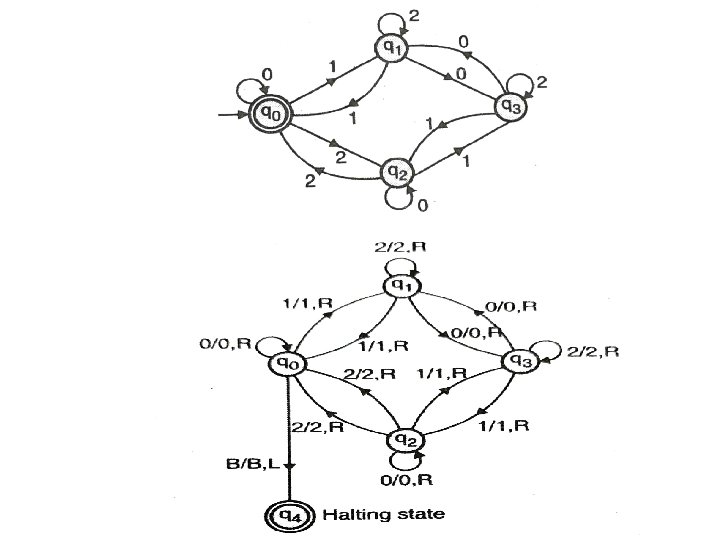
Example 1 Construct a TM for the language L = {0 n 1 n 2 n} where n≥ 1 Solution: • L = {0 n 1 n 2 n | n≥ 1} represents language where we use only 3 character, i. e. , 0, 1 and 2. In this, some number of 0's followed by an equal number of 1's and then followed by an equal number of 2's. Any type of string which falls in this category will be accepted by this language. • The simulation for 001122 can be shown as below: • Now, we will see how this Turing machine will work for 001122. Initially, state is q 0 and head points to 0 as: 0 0 1 1 2 2 B

• The move will be δ(q 0, 0) = δ(q 1, X, R) which means it will go to state q 1, replaced 0 by A and head will move to the right as: X 0 1 1 2 2 B • The move will be δ(q 1, 0) = δ(q 1, 0, R) which means it will not change any symbol, remain in the same state and move to the right as: X 0 1 1 2 2 B • The move will be δ(q 1, 1) = δ(q 2, Y, R) which means it will go to state q 2, replaced 1 by B and head will move to right as: X 0 Y 1 2 2 B

• The move will be δ(q 2, 1) = δ(q 2, 1, R) which means it will not change any symbol, remain in the same state and move to right as: X 0 Y 1 2 2 B • The move will be δ(q 2, 2) = δ(q 3, Z, R) which means it will go to state q 3, replaced 2 by C and head will move to right as: X 0 Y 1 Z 2 B • Now move δ(q 3, 2) = δ(q 3, 2, L) and δ(q 3, Z) = δ(q 3, Z, L) and δ(q 3, 1) = δ(q 3, 1, L) and δ(q 3, Y) = δ(q 3, Y, L) and δ(q 3, 0) = δ(q 3, 0, L), and then move δ(q 3, X) = δ(q 0, X, R), it means will go to state q 0, replaced X by X and head will move to right as: X 0 Y 1 Z 2 B

• The move will be δ(q 0, 0) = δ(q 1, X, R) which means it will go to state q 1, replaced 0 by X, and head will move to right as: X X Y 1 Z 2 B • The move will be δ(q 1, Y) = δ(q 1, Y, R) which means it will not change any symbol, remain in the same state and move to right as: X X Y 1 Z 2 B • The move will be δ(q 1, 1) = δ(q 2, Y, R) which means it will go to state q 2, replaced 1 by B and head will move to right as: X X Y Y Z 2 B

• The move will be δ(q 2, Z) = δ(q 2, Z, R) which means it will not change any symbol, remain in the same state and move to right as: X X Y Y Z 2 B • The move will be δ(q 2, 2) = δ(q 3, Z, L) which means it will go to state q 3, replaced 2 by Z and head will move to left until we reached A as: X X Y Y Z Z B • Immediately before B is A that means all the 0's are market by A. So we will move right to ensure that no 1 or 2 is present. The move will be δ(q 2, y) = (q 4, y, R) which means it will go to state q 4, will not change any symbol, and move to right as: X X Y Y Z Z B

• The move will be (q 4, Y) = δ(q 4, Y, R) and (q 4, Z) = δ(q 4, Z, R) which means it will not change any symbol, remain in the same state and move to right as: X X Y Y Z Z B • The move δ(q 4, X) = (q 5, X, R) which means it will go to state q 5 which is the HALT state and HALT state is always an accept state for any TM. X X Y Y Z Z B

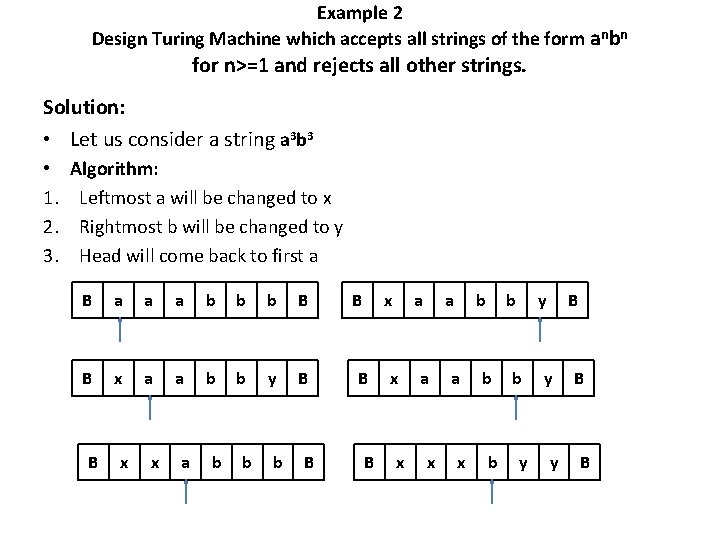
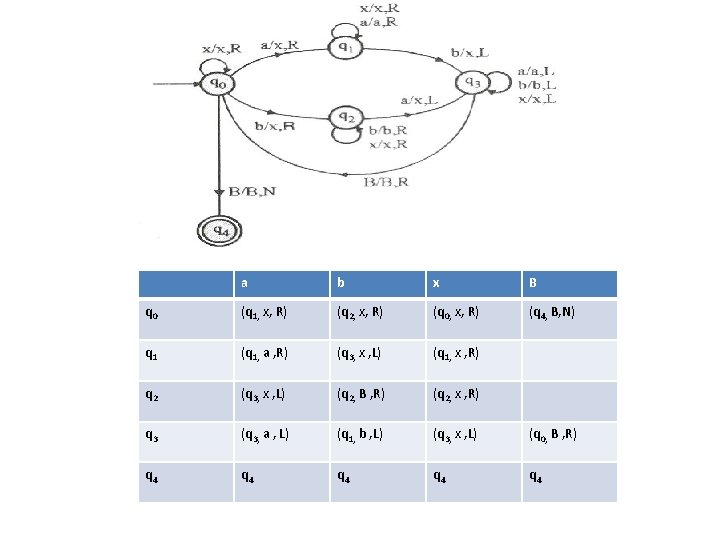
Example 2 Design Turing Machine which accepts all strings of the form anbn for n>=1 and rejects all other strings. Solution: • Let us consider a string a 3 b 3 • 1. 2. 3. Algorithm: Leftmost a will be changed to x Rightmost b will be changed to y Head will come back to first a B a a a b b b B B x a a b b y B B x x a b b b B B x B B a x x a a x b b b y B y y B B

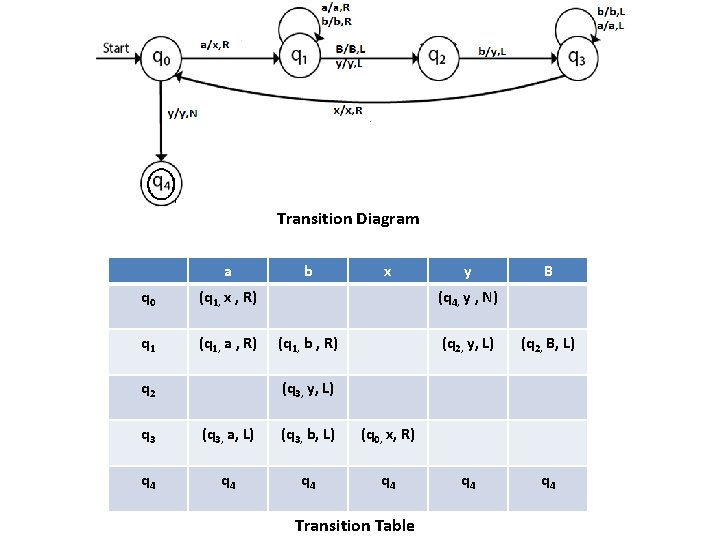
Transition Diagram a q 0 (q 1, x , R) q 1 (q 1, a , R) q 2 b x y B (q 4, y , N) (q 1, b , R) (q 2, y, L) (q 2, B, L) q 4 (q 3, y, L) q 3 (q 3, a, L) (q 3, b, L) (q 0, x, R) q 4 q 4 Transition Table

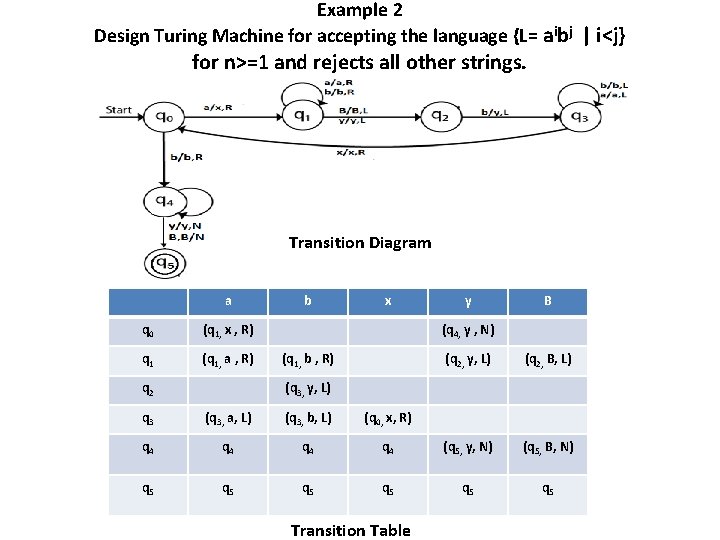
Example 2 Design Turing Machine for accepting the language {L= aibj | i<j} for n>=1 and rejects all other strings. Transition Diagram a q 0 (q 1, x , R) q 1 (q 1, a , R) q 2 b x y B (q 4, y , N) (q 1, b , R) (q 2, y, L) (q 2, B, L) (q 3, y, L) q 3 (q 3, a, L) (q 3, b, L) (q 0, x, R) q 4 q 4 (q 5, y, N) (q 5, B, N) q 5 q 5 q 5 Transition Table

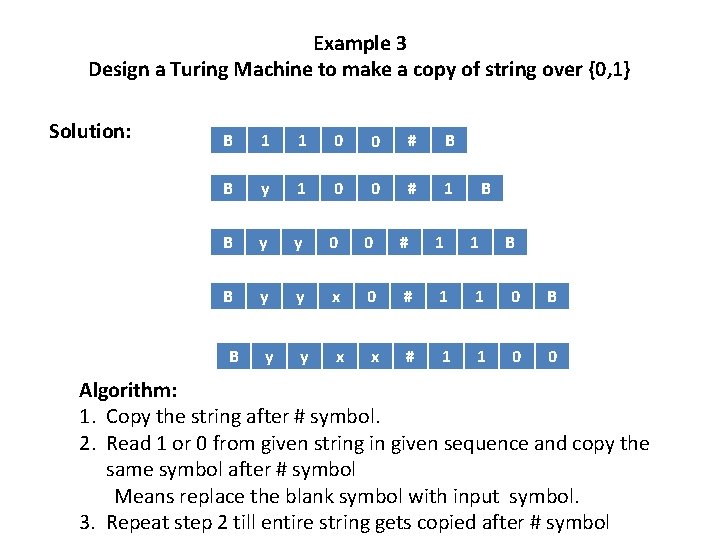
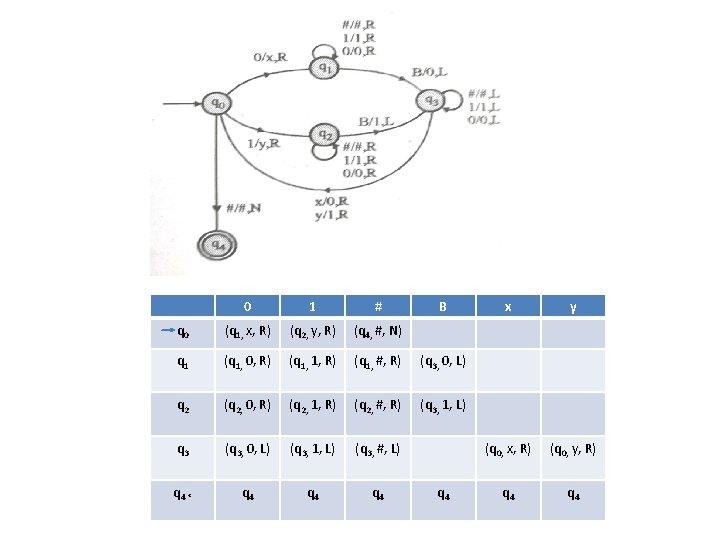
Example 3 Design a Turing Machine to make a copy of string over {0, 1} Solution: B 1 1 0 0 # B B y 1 0 0 # 1 B y y 0 0 # 1 1 B B y y x 0 # 1 1 0 B y y x x # 1 1 0 0 B B Algorithm: 1. Copy the string after # symbol. 2. Read 1 or 0 from given string in given sequence and copy the same symbol after # symbol Means replace the blank symbol with input symbol. 3. Repeat step 2 till entire string gets copied after # symbol

0 1 # B q 0 (q 1, x, R) (q 2, y, R) (q 4, #, N) q 1 (q 1, 0, R) (q 1, 1, R) (q 1, #, R) (q 3, 0, L) q 2 (q 2, 0, R) (q 2, 1, R) (q 2, #, R) (q 3, 1, L) q 3 (q 3, 0, L) (q 3, 1, L) (q 3, #, L) q 4 * q 4 q 4 x y (q 0, x, R) (q 0, y, R) q 4

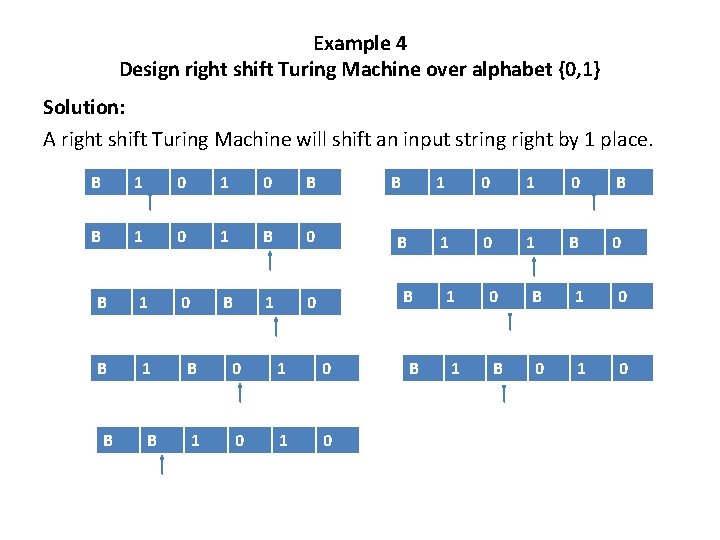
Example 4 Design right shift Turing Machine over alphabet {0, 1} Solution: A right shift Turing Machine will shift an input string right by 1 place. B 1 0 B B 1 0 1 B 0 B 1 B 0 1 0 B B B 1 0 1 B 0 1 0

B B 1 0 0 1 B q 0 (q 0 , 0, R) (q 0 , 1, R) (q 1 , B, L) q 1 (q 2 , B, R) (q 3 , B, R) (q 5 , B, N) q 2 (q 4 , 0, L) q 3 (q 4 , 1, L) q 4 (q 1 , B, L) q 5 * q 5 q 5

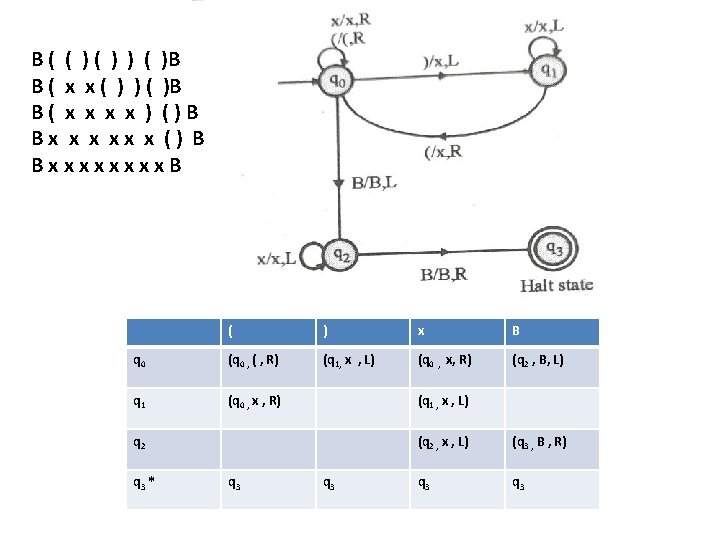
Example 5 Construct a TM for checking well formedness of parenthesis Solution: Consider the input as (()())() B ( ( ) ) ( ) B B ( x x ( ) ) ( ) B B( x x ) ( ) B B x x x x B Algorithm: 1. In each cycle leftmost ‘)’ is written as ‘x’ then head moves left to locate the nearer ‘(‘ and it is changed to ‘x’ 2. Repeat this procedure till all parenthesis get replaced with x.

B ( ( ) ) ( )B B ( x x ( ) ) ( )B B( x x ) ()B Bx x x xx x () B Bxxxx. B ( ) x B q 0 (q 0 , ( , R) (q 1, x , L) (q 0 , x, R) (q 2 , B, L) q 1 (q 0 , x , R) (q 1 , x , L) q 2 q 3 * q 3 (q 2 , x , L) (q 3 , B , R) q 3

Example 6 Design Turing Machine to check whether a string over {a, b} contains equal number of a’s and b’s Algorithm: 1. Locate first a or b. 2. If it is ‘a’ then locate ‘b’ and rewrite them as x. 3. If it is ‘b’ then locate ‘a’ and rewrite them as x. 4. Repeat the steps 1 to 3 till every a or b is rewritten as x.

a b x B q 0 (q 1, x, R) (q 2, x, R) (q 0, x, R) (q 4, B, N) q 1 (q 1, a , R) (q 3, x , L) (q 1, x , R) q 2 (q 3, x , L) (q 2, B , R) (q 2, x , R) q 3 (q 3, a , L) (q 1, b , L) (q 3, x , L) (q 0, B , R) q 4 q 4 q 4

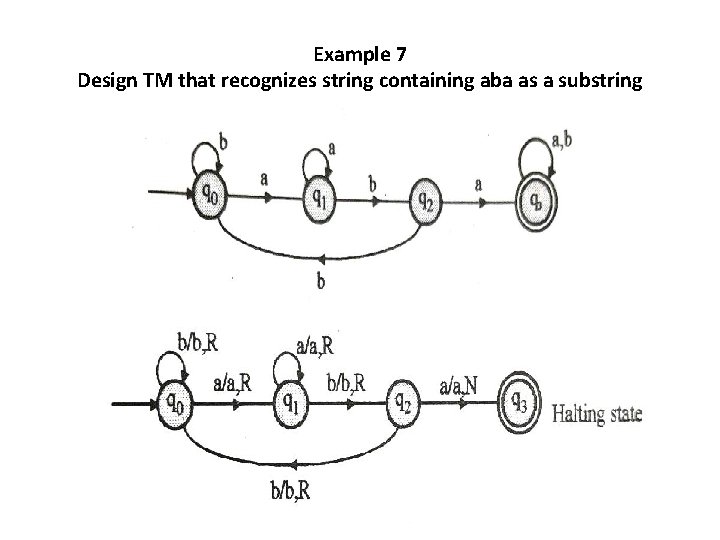
Example 7 Design TM that recognizes string containing aba as a substring

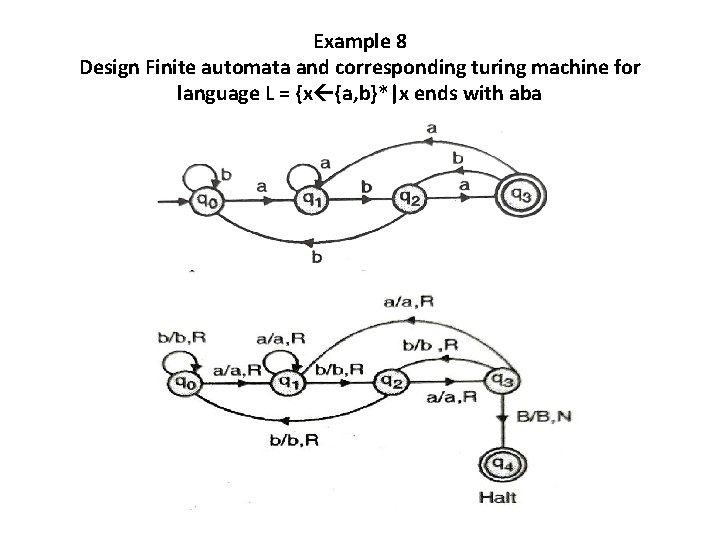
Example 8 Design Finite automata and corresponding turing machine for language L = {x {a, b}*|x ends with aba

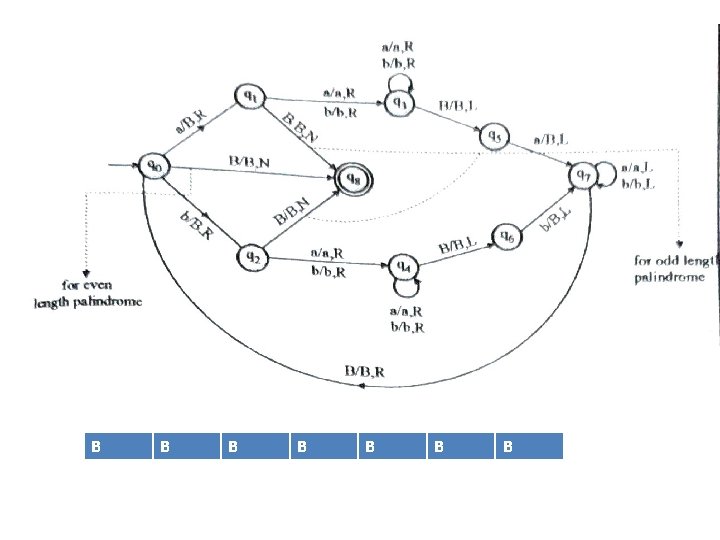
Example 8 Design Turing Machine which recognizes palindromes over alphabet {a, b} Solution: • Palindrome can be of following form ww. R , waw. R or wbw. R • E. g L = {a, b, aa, bb, aba , bab, aaa, bbb, abba, baab, abaaba, …. . } Algorithm: 1. Match first character with last character and erase both characters. 2. Repeat step 1 till all characters get erased.

a b a B B b a a b B B B B a a b B B B a B B B B a a B B B B

B B B B

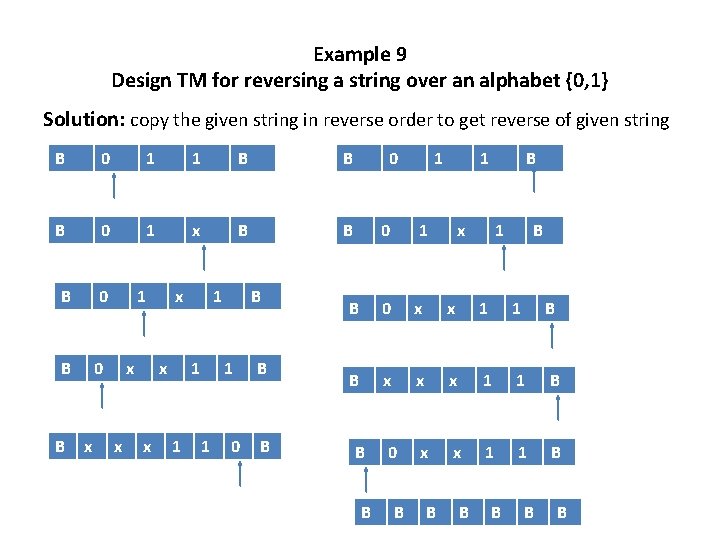
Example 9 Design TM for reversing a string over an alphabet {0, 1} Solution: copy the given string in reverse order to get reverse of given string B 0 1 1 B B B 0 1 x B B B 0 B B 1 0 x x x 1 1 1 B 1 1 0 B B 0 1 1 B 0 x x 1 1 B B x x x 1 1 B 0 x x 1 1 B B B x B 1 B B

B 1

Turing Machine as a Computer Function • Turing machine can be used for computation. • It can perform the several operations like addition, subtraction, multiplication and division. • Number representation: • The unary number system is often used while computing a function using Turing Machine. • The unary system uses only one symbol. Representation of same decimal numbers in unary system is given below: • Decimal Number Unary Number 0 B (blank symbol) 1 0 2 00 3 000 n 0…………. n times 0

Example 1 Design Turing Machine to find 2’s complement of binary machine. Solution: • The 2’s complement of binary number can be found by not changing bits from right end till the 1 st one then complement all remaining bits. • Example: • 0 0 1 0 0 2’s complement is 11011100 Complement the bits • 1. 2. 3. No change Algorithm: Locate the last bit (right most bit) Move left till first 1. Complement the remaining bits while moving left till blank symbol.

B 0 0 1 0 0 B B 0 0 1 0 0 B 0 0 0 1 0 0 B B 0 0 1 1 0 0 B B 0 0 1 1 0 0 B B 0 0 0 1 1 1 B 0 1 1 1 0 0 B B 1 1 0 1 1 1 0 0 B

0 1 B q 0 (q 0, 0 , R) (q 0, 1 , R) (q 1, B , L) q 1 (q 1, 0 , L) (q 2, 1 , L) (q 3, B , R) q 2 (q 2, 1 , L) (q 2, 0 , L) (q 3, B , R) q 3* q 3 q 3

Example 2 Design Turing Machine to compute proper subtraction of two unary numbers. The proper subtraction function f is defined as follows: f(m, n) = m-n if m>n else 0 Solution: • Let us consider two numbers 4 (0000) and 2(00) • We will take bigger number at left hand side and smaller number at right hand side on tape. Algorithm: 1. Erase leftmost 0. 2. Erase rightmost 0. 3. Repeat step 1 and 2 till all 0’s at right hand side get erased.

B 0 0 # 0 0 B B B 0 0 0 # 0 B B B B B 0 0 # B B B

Example 3 Compute multiplication of two unary numbers. Solution: • Lets consider two numbers as 3 and 4. • Here we will copy four(second number) zeros for every cycle and we repeat this step for 3(first number) cycles B 0 0 0 # B B x 0 0 # x 0 0 0 # 0 B Cycle 1: 1 *4 = 4 B x 0 0 # 0 0 B B x 0 0 # 0 0 x 0 # 0 0 0 B B x 0 0 # 0 0 0 x # 0 0 B B B 0 0 x x 0 0 # # x 0 0 0 0 x # # 0 0 0 0 0 B 0 0 B B B 0 0 0 0 x x # # x 0 0 0 x 0 0 x # # 0 0 0 0 0 0 0 0 Cycle 2: 2*4 = 8 0 0 B 0 B Cycle 3: 3*4 = 12 0 0 B 0 0 0 B

B 0 0 0 #0 0 # 0 0 0 B B

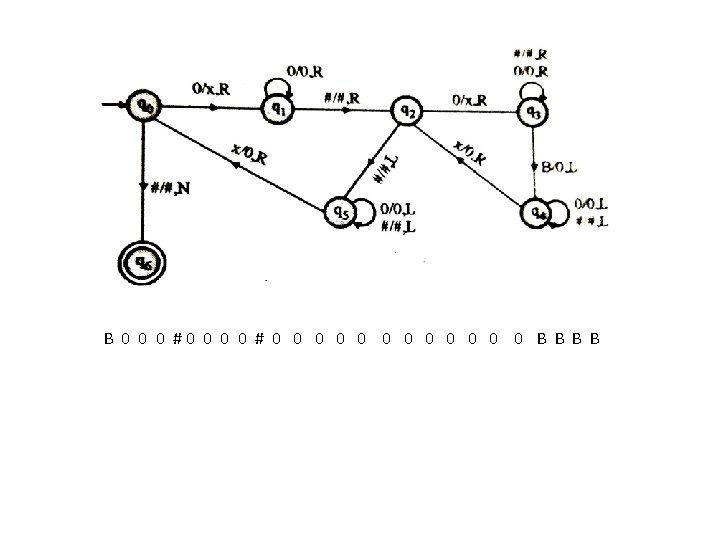
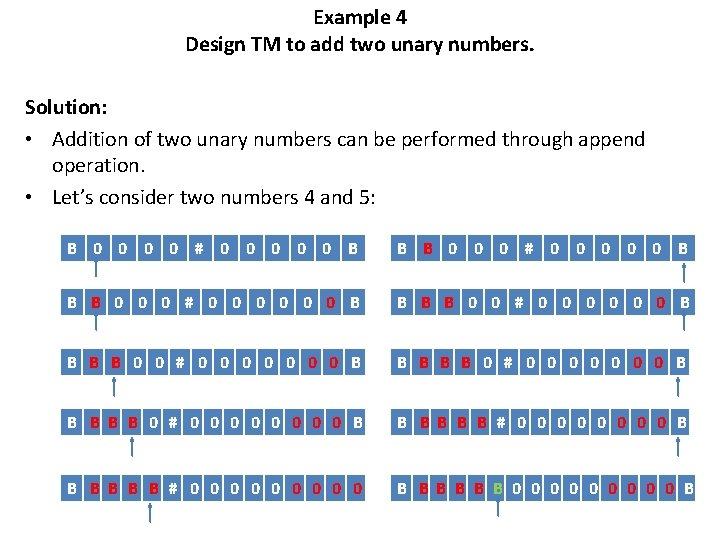
Example 4 Design TM to add two unary numbers. Solution: • Addition of two unary numbers can be performed through append operation. • Let’s consider two numbers 4 and 5: B 0 0 # 0 0 0 0 0 B B B 0 0 0 # 0 0 0 B B B B 0 0 # 0 0 0 0 B B B B B 0 # 0 0 0 0 B B B # 0 0 0 0 0 B BB B 0 0 0 0 0 B

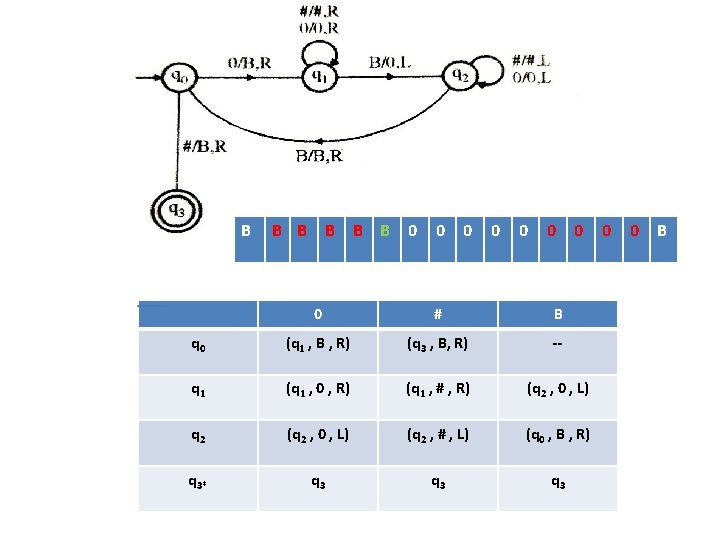
B B B 0 0 0 0 # B q 0 (q 1 , B , R) (q 3 , B, R) -- q 1 (q 1 , 0 , R) (q 1 , # , R) (q 2 , 0 , L) q 2 (q 2 , 0 , L) (q 2 , # , L) (q 0 , B , R) q 3* q 3 q 3 0 0 B

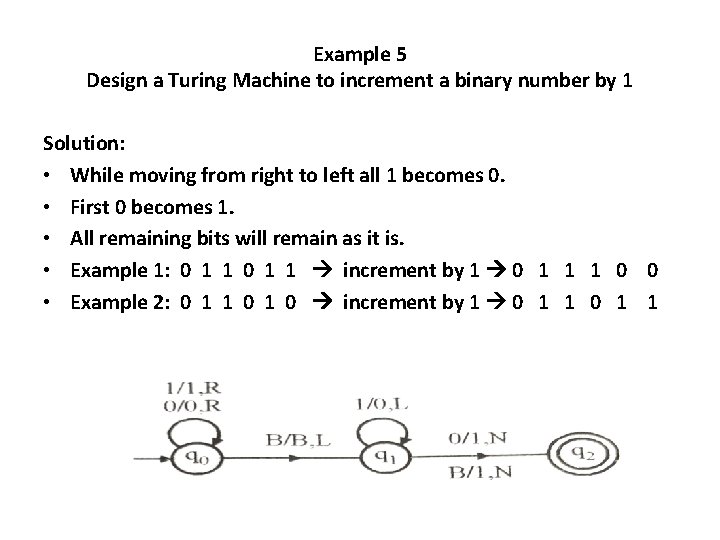
Example 5 Design a Turing Machine to increment a binary number by 1 Solution: • While moving from right to left all 1 becomes 0. • First 0 becomes 1. • All remaining bits will remain as it is. • Example 1: 0 1 1 increment by 1 0 1 1 1 0 0 • Example 2: 0 1 1 0 increment by 1 0 1 1

0 1 B q 0 (q 0 , R) (q 0 , 1 , R) (q 1 , B , L) q 1 (q 2 , 1 , N) (q 1 , 0 , L) (q 2 , 1, N) q 2* q 2 q 2

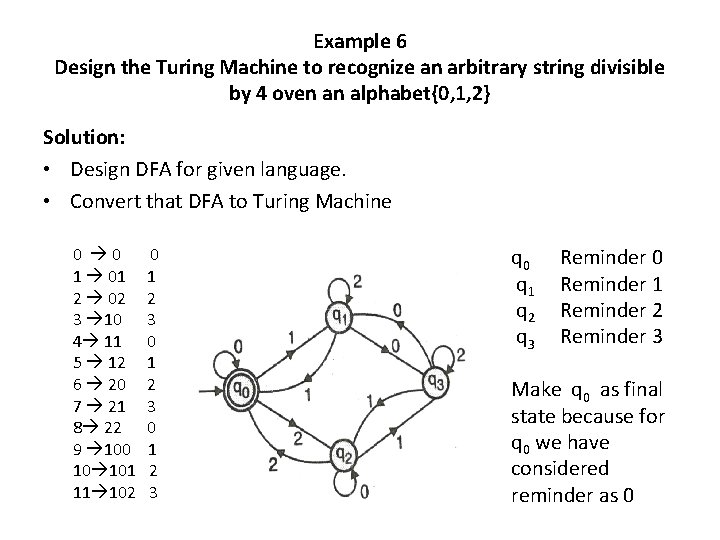
Example 6 Design the Turing Machine to recognize an arbitrary string divisible by 4 oven an alphabet{0, 1, 2} Solution: • Design DFA for given language. • Convert that DFA to Turing Machine 0 0 1 01 2 02 3 10 4 11 5 12 6 20 7 21 8 22 9 100 10 101 11 102 0 1 2 3 q 0 q 1 q 2 q 3 Reminder 0 Reminder 1 Reminder 2 Reminder 3 Make q 0 as final state because for q 0 we have considered reminder as 0

Extension of Turing Machine • In standard Turing Machine the tape is semi-infinite. It is bounded on left and unbounded on right side. • Some extensions of Turing Machine are: 1. Two way infinite Turing Machine 2. Turing Machine with multiple heads 3. Multi-tape Turing Machine. 4. K-dimension Tape 5. Non- Deterministic Turing Machine

Two -way Infinite Turing Machine • In Two way Turing Machine, there is an infinite sequence of blanks on each side of the input string. • Infinite tape of two-way infinite tape Turing machine is unbounded in both directions left and right. • ……B B a b a B B…….

Turing Machine with Multiple Heads • Turing machine with single tape can have Multiple Heads. • Let us consider the Turing Machine with two heads H 1 and H 2. • Each head is capable of performing read/write/move operation independently. • Bababaa. BBBB H 1 H 2 • The transition behavior of 2 -head one tape Turing Machine can be defined as : • δ(state, symbol under H 1, symbol under H 2) = (new state, (S 1, M 1), (S 2, M 2) where, S 1 is the symbol to be written in the cell under H 1. M 1 is the movement (L , R, N) of H 1 S 2 is the symbol to be written in the cell under H 2. M 2 is the movement (L , R, N) of H 2.

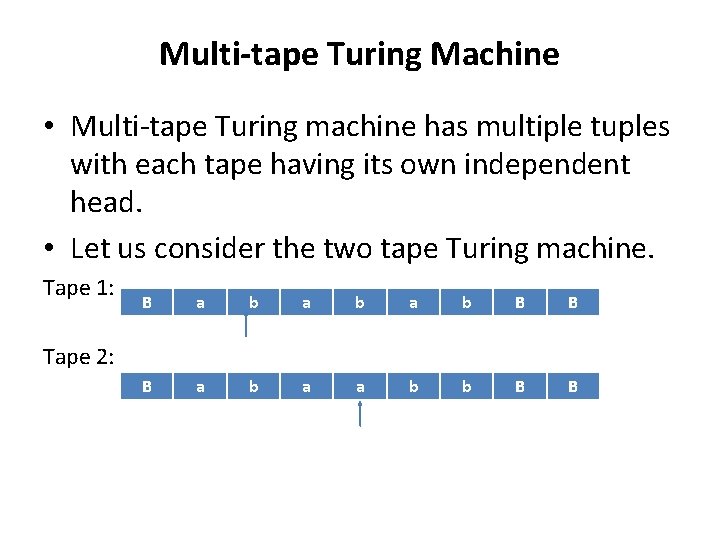
Multi-tape Turing Machine • Multi-tape Turing machine has multiple tuples with each tape having its own independent head. • Let us consider the two tape Turing machine. Tape 1: B a b a b B B B a b a a b b B B Tape 2:

Multi-tape Turing Machine • The transition Behavior of two tape Turing Machine can be defined as : • δ( q 1, a 2) = (q 2, (S 1, M 1), (S 2, M 2)) • Where, • q 1 is current state. • q 2 is next state. • a 1 is the symbol under head on tape 1. • a 2 is the symbol under head on tape 2. • S 1 is the symbol written in the current cell on tape 1. • S 2 is the symbol written in the current cell on tape 2. • M 1 is the movement (L, R, N) of head on tape 1. • M 2 is the movement (L, R, N) of head on tape 2.

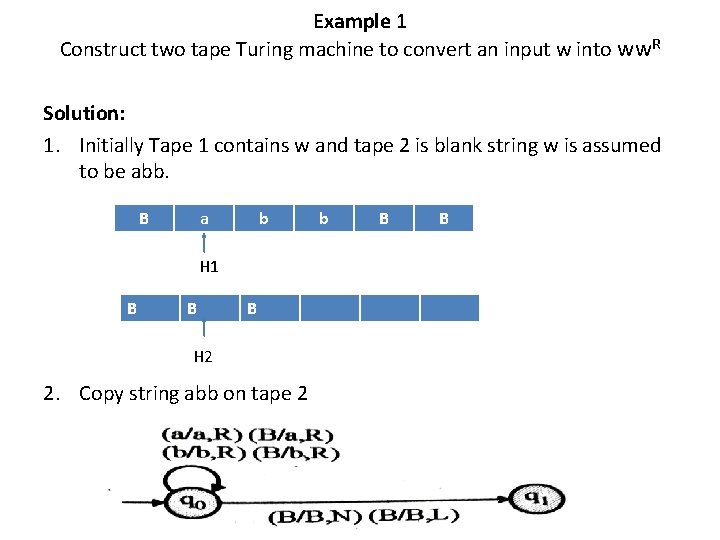
Example 1 Construct two tape Turing machine to convert an input w into ww. R Solution: 1. Initially Tape 1 contains w and tape 2 is blank string w is assumed to be abb. B a b H 1 B B B H 2 2. Copy string abb on tape 2 b B B

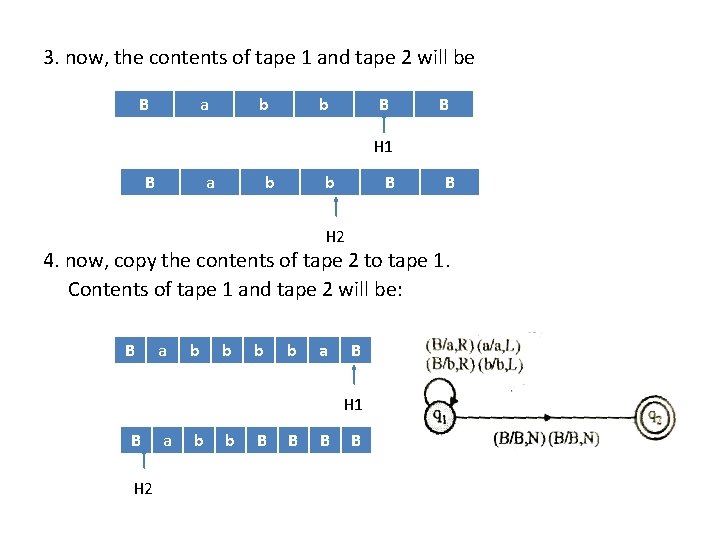
3. now, the contents of tape 1 and tape 2 will be B a b b B B H 1 B a b b B H 2 B 4. now, copy the contents of tape 2 to tape 1. Contents of tape 1 and tape 2 will be: B a b b a B H 1 B H 2 a b b B B

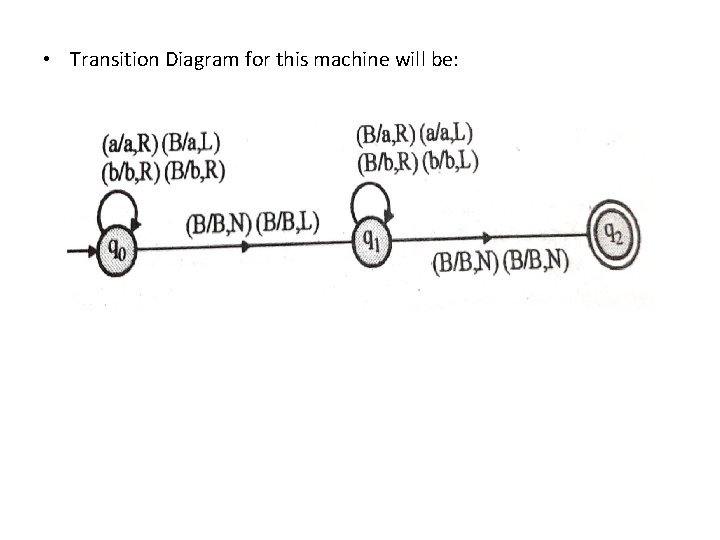
• Transition Diagram for this machine will be:

Non Deterministic Turing Machine • It is a powerful feature. • A non deterministic Turing machine might have , certain combinations of state and symbol under the head, more than one possible choice of behavior. • Non deterministic does not make machine more powerful. • For every non deterministic Turing Machine there is a equivalent deterministic Turing Machine. • It is easy to design Non deterministic TM for certain class of problems. • A string is said to be accepted by NDTM, if there is at least one sequence of moves that takes the machine to final state. • Example: • The transition behavior of state q 0 for above TM • δ(q 0 , a) = {(q 0 , a, R) (q 1 , x , R)

Universal TM • A general purpose computer can be programmed to solve different type of problems. • TM can behave like a general purpose computer. • A general purpose computer solves the problem given as : • A program is written in high level language and a machine code is obtained with the help of compiler. • Machine code is loaded in main memory. • Input to program can also be loaded in memory. • Program stored in memory is executed line by line. • Execution involves reading line of code pointed by IP, decoding the code and executing it. • Similar approach is followed in Turing Machine. • Such a Turing Machine is known as Universal Turing Machine.

• Universal Turing machine can solve all types of solvable problems. • Turing Machine M is designed to solve a particular problem p, can be specified as: 1. the initial state q 0 of TM M. 2. The transition function δ of M can be specified as given: • If the current state of M is qi and the symbol under head is ai then machine moves to state qi while changing ai to aj. • The move of tape head may be : • 1. To left 2. To right 3. No move • Universal Turing Machine can be able to simulate every TM. • Simulation of TM will involve: Ø Encoding behavior of particular TM as a program. Ø Execution of above program by Universal TM.

• The move of the form (qi , ai , qj, aj, mf ) can be represented as 10 i+1 10 i 10 j+1 10 j 10 k • Where k = 1 if move is to left k = 2 if move is to right k =3 if no move • The state q 0 is represented by 0, state q 1 is represented by 00, state qn is represented by 0 n+1. jfjf • The first symbol can be represented by 0, second symbol can be represented by 00 and so on. • Two elements of tuple representing a move are separated by 1. • Two moves are separated by 11.

Execution of UTM • We can assume that UTM has 3 tape Turing Machine. 1. Input in written on first tape. 2. Moves of TM are in encoded form and it is written on second tape. 3. The current state of TM is written third tape. • The control unit of Turing Machine by counting number of 0’s between 1’s can find out current symbol under head. • It can find current state of tape 3. • It can locate the appropriate move based on current input and current state from tape 2. • Now, control unit can extract the following information from tape 2. Ø next sate Ø Next symbol to be written Ø Move of head. Based on this information control unit can take appropriate action.

Linear Bounded Automata • Linear Bounded Automata(LBA) restricts the length of tape. • LBA is important as the set of context sensitive language accepted by it. • Linear Bounded Automata is same as non deterministic Turing Machine. • Turing Machine accept in following: 1. There is a special symbol < making left end of tape. 2. There is a special symbol > making a right end of tape. 3. The head is not allowed to move beyond these end markers. 4. The head is not allowed to change these end markers. • The LBA can be denoted by: M = (Q , ∑ , Γ , δ , q 0 , F , < , >) • Where < and > are symbols in ∑ , the left and right end markers respectively. Q , ∑ , Γ , δ , q 0 and F are same as non deterministic TM