Turing Completeness Relevance to programming languages How can

Turing Completeness Relevance to programming languages: How can we measure the generality of a language? (One answer: by determining whether or not the language is “Turing complete. ”) Historical perspective. Examples of Turing Machines. Formal definition of Turing Completeness. Applying Turing Completeness. CSE 341 -- S. Tanimoto Turing Completeness 1

Historical Perspective In the 1940 s, Alan Turing and Emil Post were investigating the question of which mathematical functions are theoretically computable by mechanical devices. One question they faced: “What is a computable function? ” Are all mathematical functions computable? (Answer: no) Formal models of computers and computation. . . CSE 341 -- S. Tanimoto Turing Completeness 2

The Turing Machine Turing proposed an abstract model of a mechanical computing device, a sort of “tape automaton” with ability to read and write symbols on the tape and move the tape left and right. We now call it a Turing Machine in Turing’s honor. CSE 341 -- S. Tanimoto Turing Completeness 3

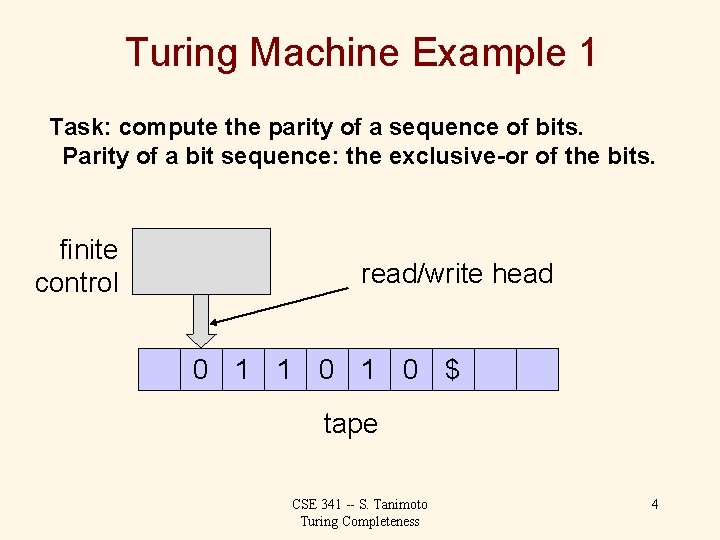
Turing Machine Example 1 Task: compute the parity of a sequence of bits. Parity of a bit sequence: the exclusive-or of the bits. finite control read/write head 0 1 1 0 $ tape CSE 341 -- S. Tanimoto Turing Completeness 4

TM Example 1 (cont) Tape alphabet: { 0, 1, $, Blank } Actions: { Left, Right, Halt } Left = move tape head left, relative to the tape. Right = “ “ “ right, “ “. Halt = stop the Turing machine. 0 1 1 0 $ CSE 341 -- S. Tanimoto Turing Completeness 5

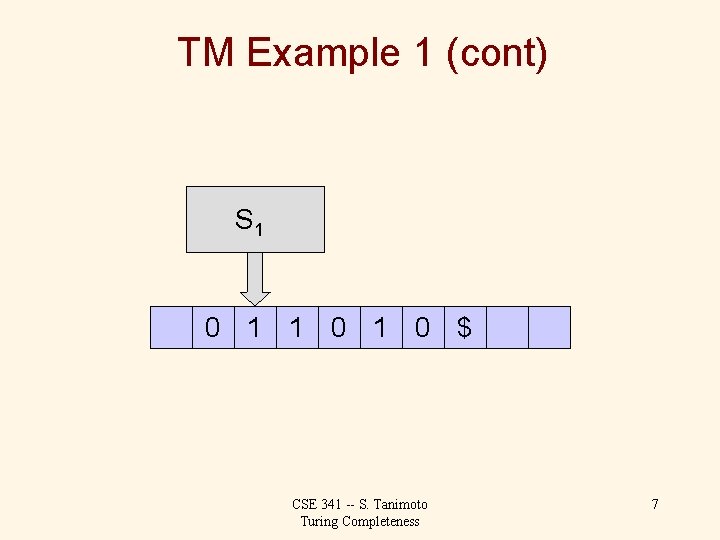
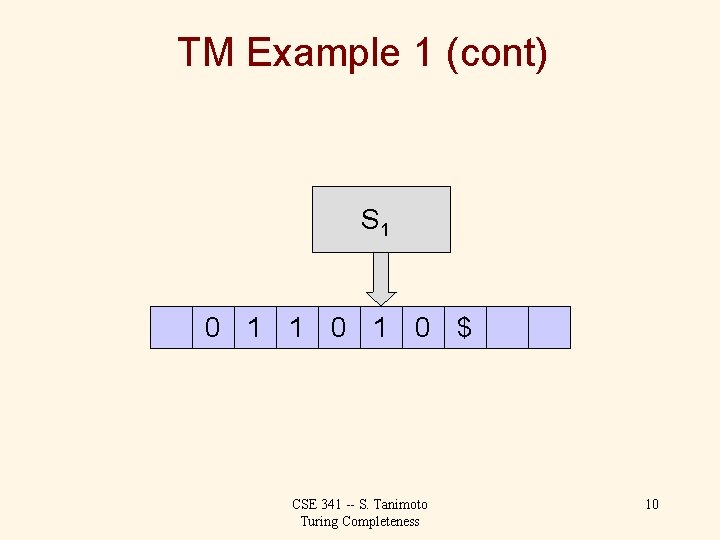
TM Example 1 (cont) Set of possible states for the finite control: S 0: initial state; parity so far is 0. S 1: parity so far is 1. Transition function: “Whenever the current tape symbol is a 1, change state, leave the symbol as it is, and move the head to the right (relative to the tape). If the current symbol is $, move right without changing state. If the current symbol is Blank, and the state is S 0, write 0 and halt, but if the current state is S 1, write 1 and halt. ” S 0 0 1 1 0 $ CSE 341 -- S. Tanimoto Turing Completeness 6

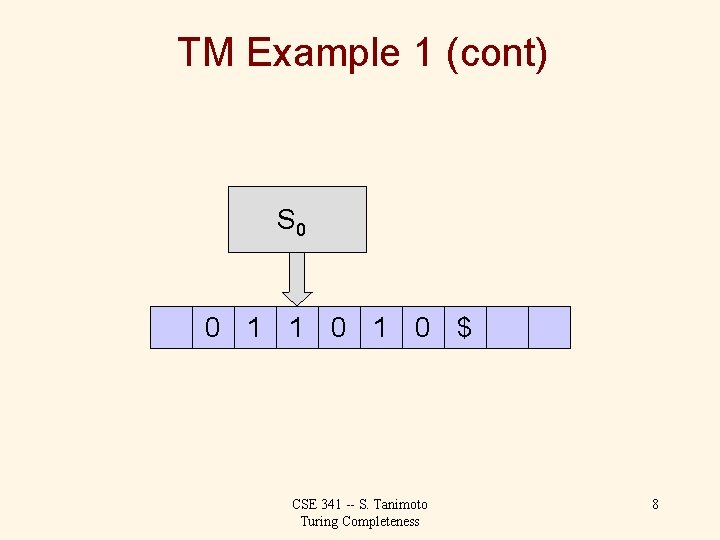
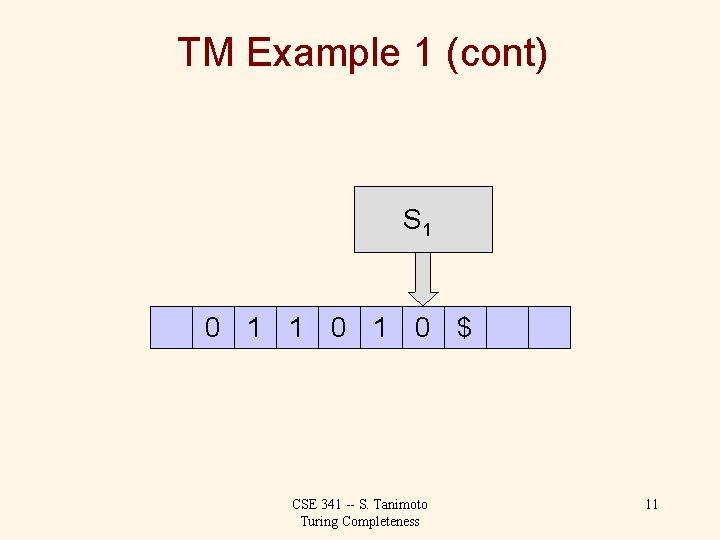
TM Example 1 (cont) S 1 0 1 0 $ CSE 341 -- S. Tanimoto Turing Completeness 7

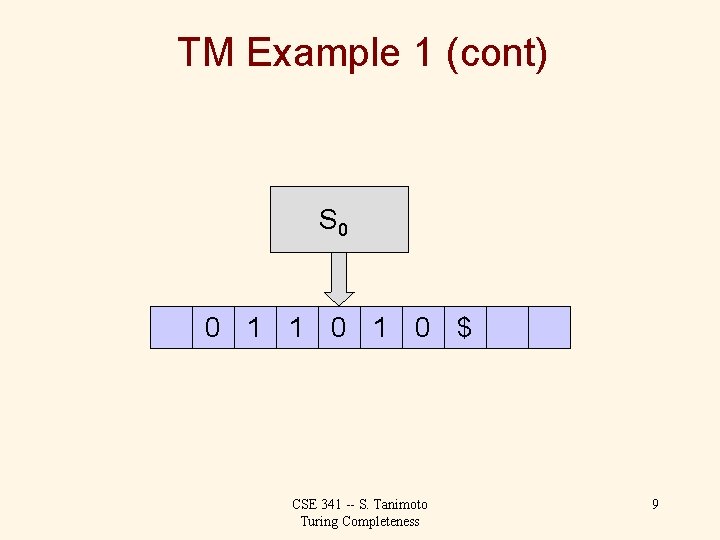
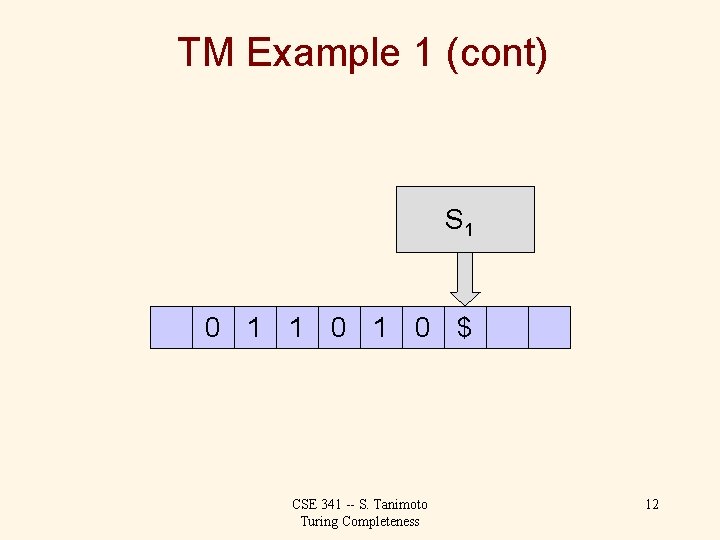
TM Example 1 (cont) S 0 0 1 1 0 $ CSE 341 -- S. Tanimoto Turing Completeness 8

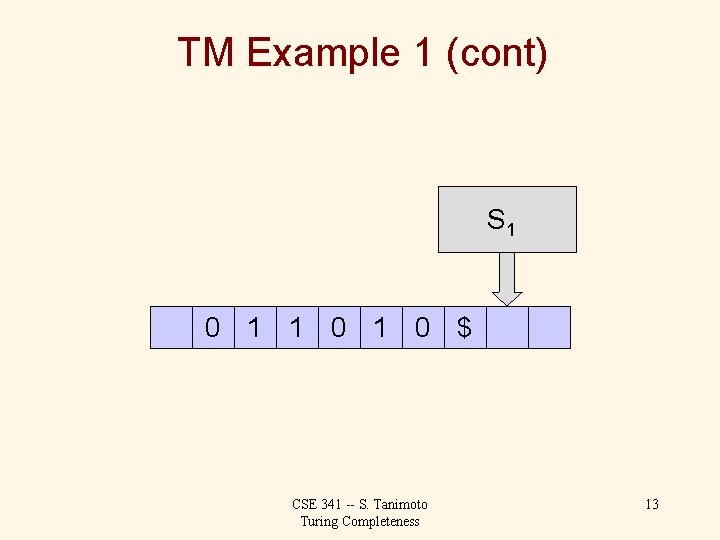
TM Example 1 (cont) S 0 0 1 1 0 $ CSE 341 -- S. Tanimoto Turing Completeness 9

TM Example 1 (cont) S 1 0 1 0 $ CSE 341 -- S. Tanimoto Turing Completeness 10

TM Example 1 (cont) S 1 0 1 0 $ CSE 341 -- S. Tanimoto Turing Completeness 11

TM Example 1 (cont) S 1 0 1 0 $ CSE 341 -- S. Tanimoto Turing Completeness 12

TM Example 1 (cont) S 1 0 1 0 $ CSE 341 -- S. Tanimoto Turing Completeness 13

TM Example 1 (cont) S 1 0 1 0 $ 1 Halt! CSE 341 -- S. Tanimoto Turing Completeness 14

Turing Machine Example 2 Compute the function f(n) = n + 1. To make this easy, let’s assume that n is represented on the tape in unary notation. Tape alphabet = { 1, Blank }, States = { S 0 }. Transition function: “If the current tape symbol is 1, move right, leaving the symbol unchanged. If the current tape symbol is Blank, write a 1 and halt. ” S 0 1 1 1 1 CSE 341 -- S. Tanimoto Turing Completeness 15

TM Example 2 (Cont) S 0 1 1 1 1 CSE 341 -- S. Tanimoto Turing Completeness 16

TM Example 2 (Cont) . . . 1 1 1 1 CSE 341 -- S. Tanimoto Turing Completeness 17

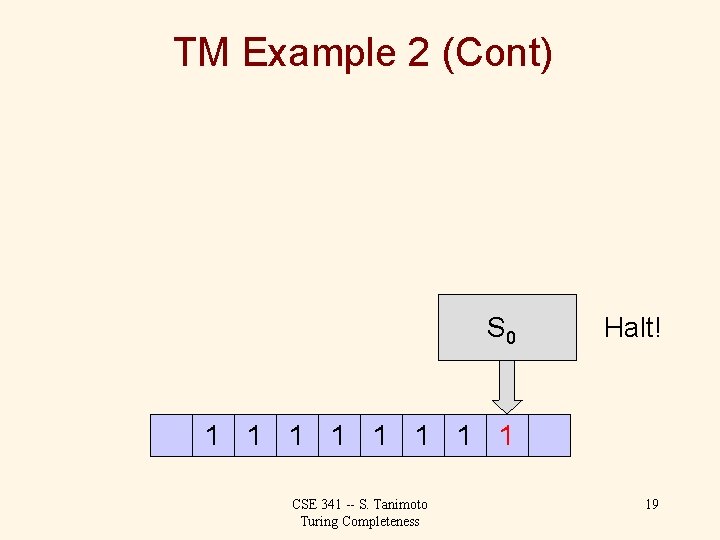
TM Example 2 (Cont) S 0 1 1 1 1 CSE 341 -- S. Tanimoto Turing Completeness 18

TM Example 2 (Cont) S 0 Halt! 1 1 1 1 CSE 341 -- S. Tanimoto Turing Completeness 19

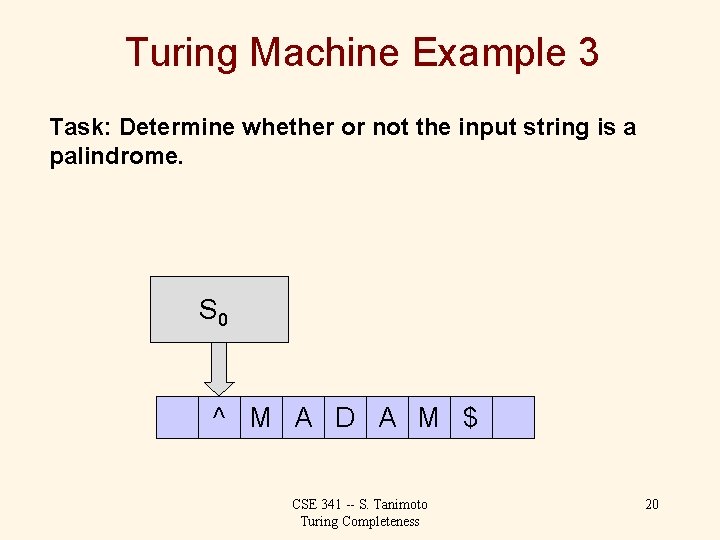
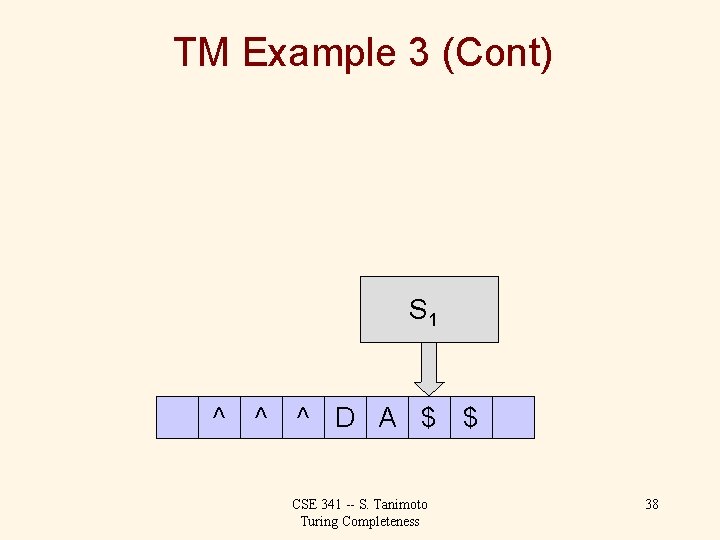
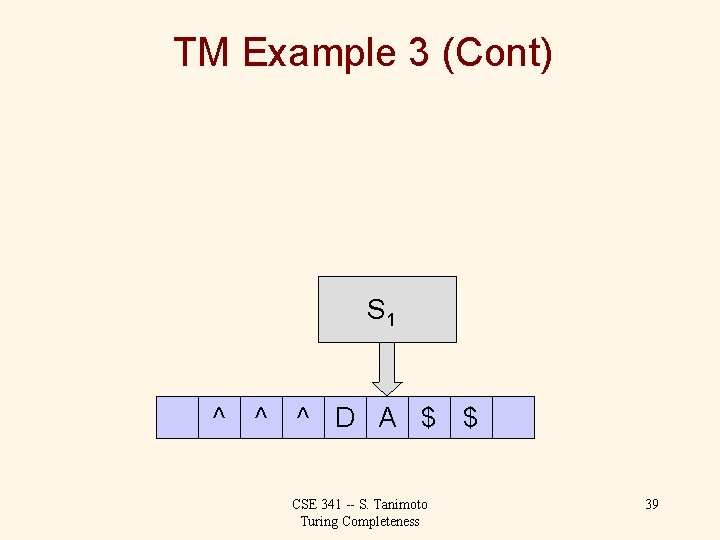
Turing Machine Example 3 Task: Determine whether or not the input string is a palindrome. S 0 ^ M A D A M $ CSE 341 -- S. Tanimoto Turing Completeness 20

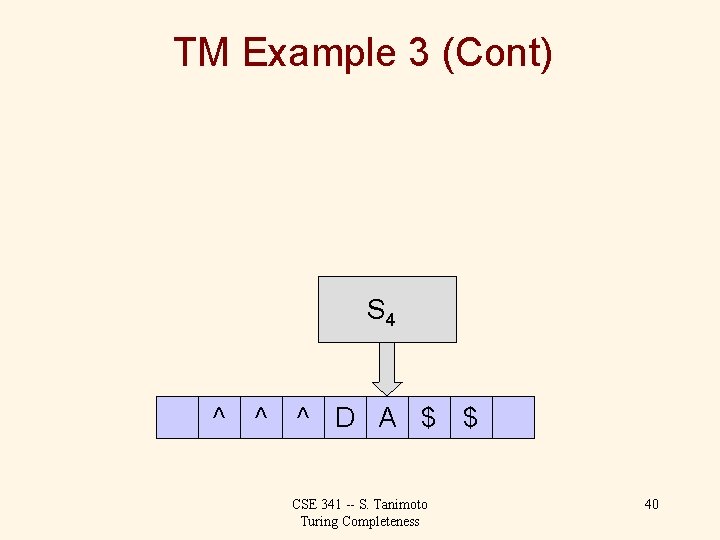
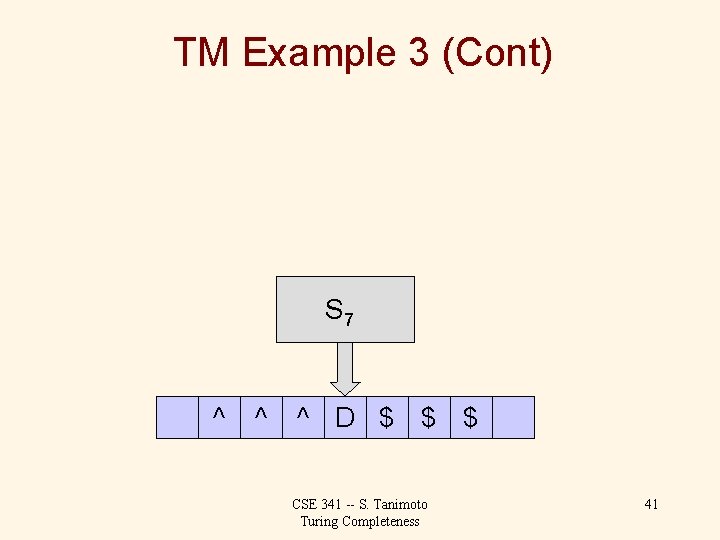
TM Example 3 (Cont) Tape alphabet: { A, D, M, ^, $, Blank } ^: left end marker, $: right end marker States: { S 0, S 1, S 2, S 3, S 4, S 5, S 6, S 7 } S 0: initial state, S 1: moving R to find A, S 2: moving R to find D, S 3: moving R to find M, S 4: stepping left for A, S 5: stepping left for D, S 6: stepping left for M, S 7: homing -- moving left to find ^ CSE 341 -- S. Tanimoto Turing Completeness 21

TM Example 3 (Cont) Transition function: Cur. State Cur. Sym. New Sym. Next State Move S 0 S 0 S 0 S 1 S 2 S 3 A D M ^ $ $ * $ * ^ ^ S 1 S 2 S 3 S 0 $ no-change S 4 S 1 S 5 S 2 S 6 S 3 CSE 341 -- S. Tanimoto Turing Completeness R R Accept L R L R 22

TM Example 3 (Cont) Transition function, continued: Cur. State Cur. Sym. New Sym. Next State Move S 4 S 4 S 5 S 5 S 6 S 6 S 7 A ^ * D ^ * M ^ * $ S 7 ^ no-change S 0 S 7 CSE 341 -- S. Tanimoto Turing Completeness L Accept Reject R L 23

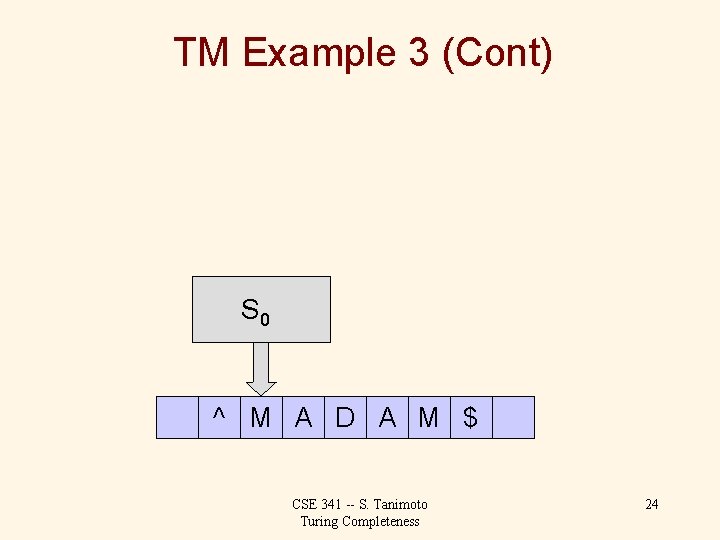
TM Example 3 (Cont) S 0 ^ M A D A M $ CSE 341 -- S. Tanimoto Turing Completeness 24

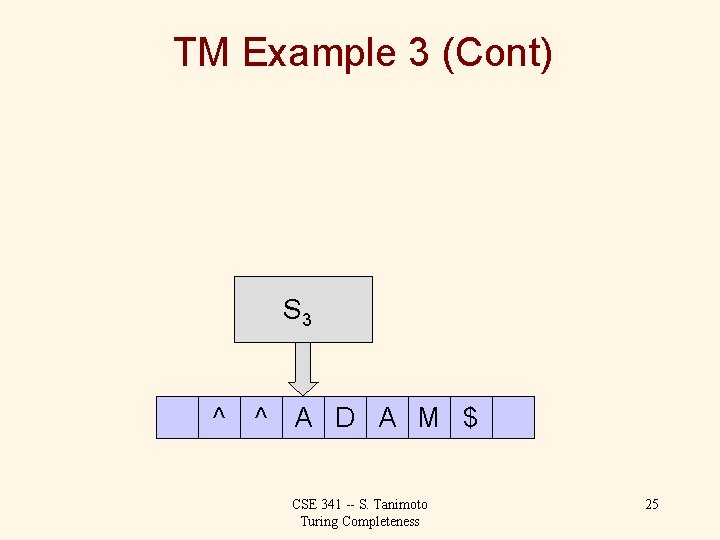
TM Example 3 (Cont) S 3 ^ ^ A D A M $ CSE 341 -- S. Tanimoto Turing Completeness 25

TM Example 3 (Cont) S 3 ^ ^ A D A M $ CSE 341 -- S. Tanimoto Turing Completeness 26

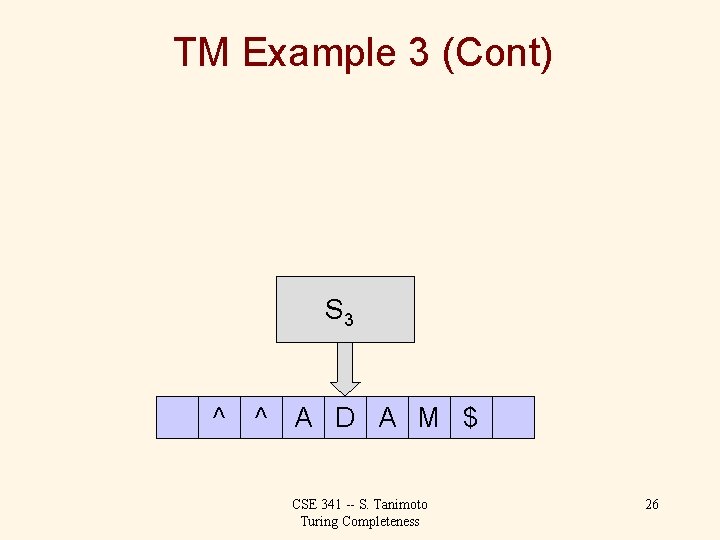
TM Example 3 (Cont) S 3 ^ ^ A D A M $ CSE 341 -- S. Tanimoto Turing Completeness 27

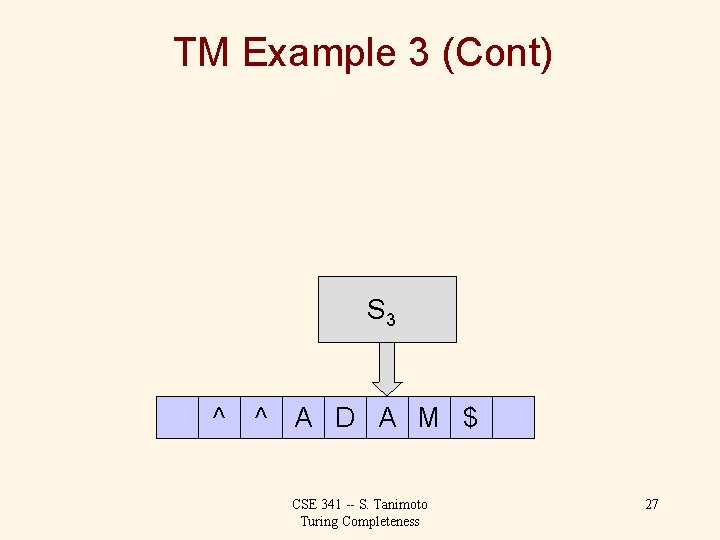
TM Example 3 (Cont) S 3 ^ ^ A D A M $ CSE 341 -- S. Tanimoto Turing Completeness 28

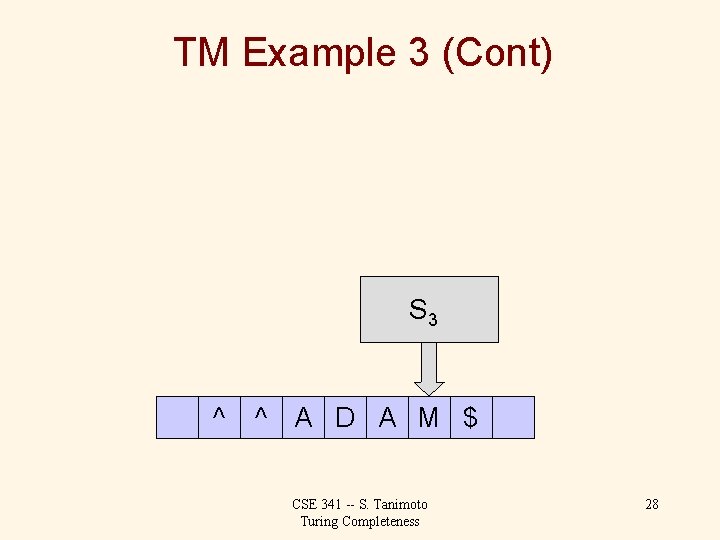
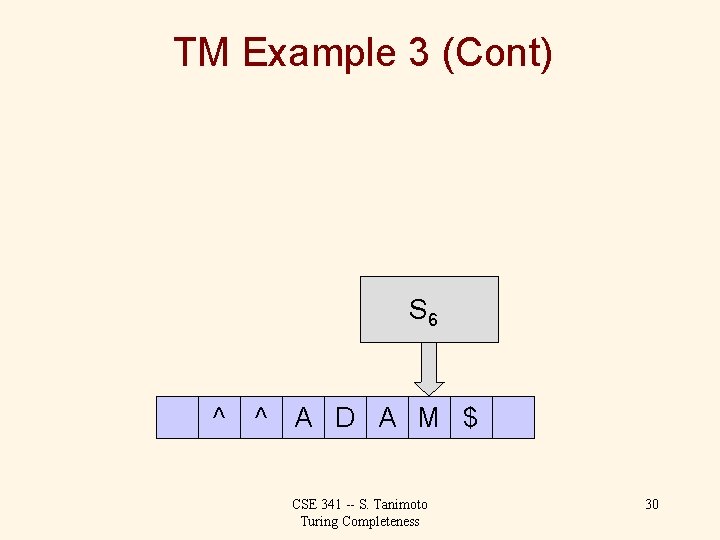
TM Example 3 (Cont) S 3 ^ ^ A D A M $ CSE 341 -- S. Tanimoto Turing Completeness 29

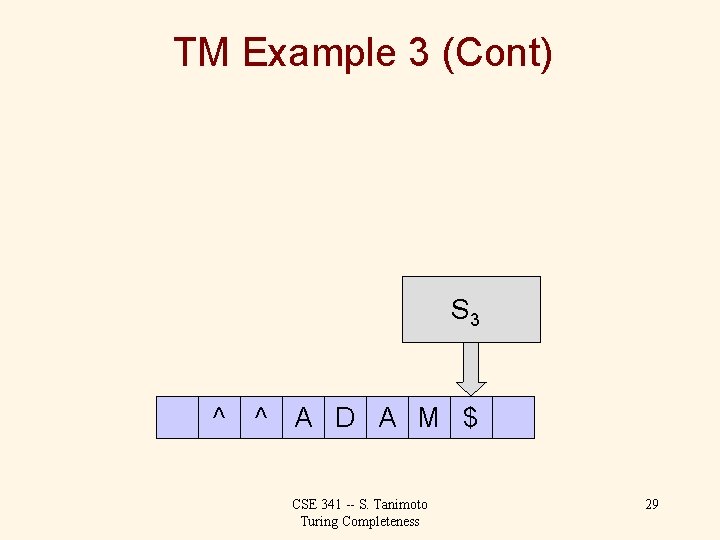
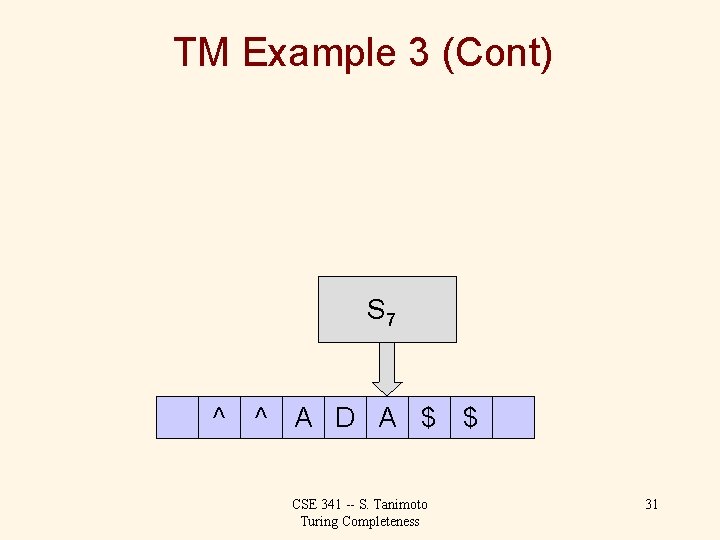
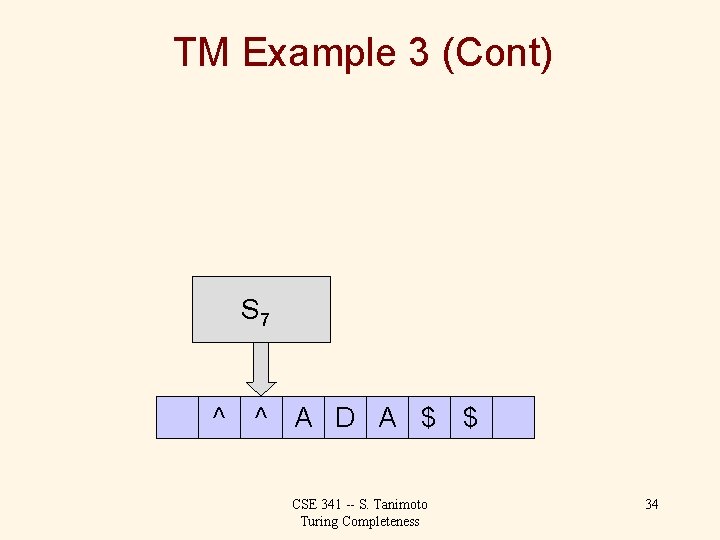
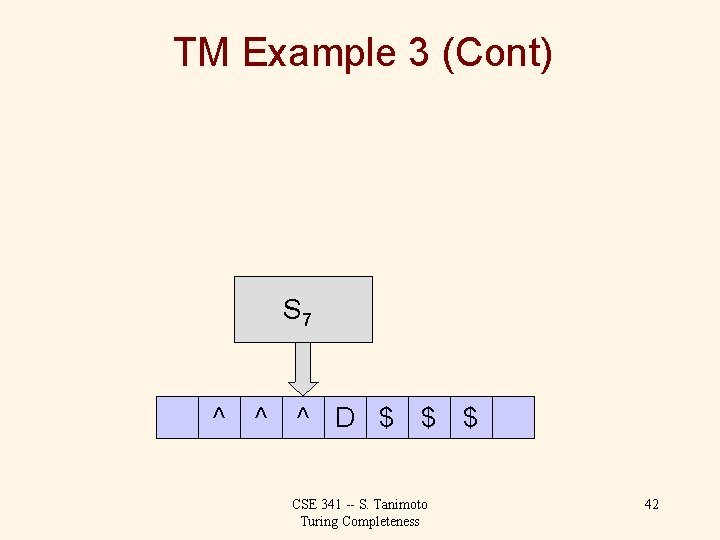
TM Example 3 (Cont) S 6 ^ ^ A D A M $ CSE 341 -- S. Tanimoto Turing Completeness 30

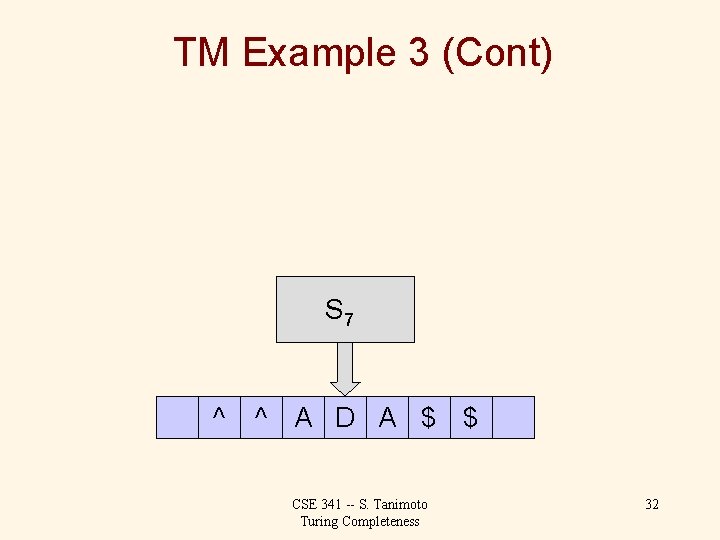
TM Example 3 (Cont) S 7 ^ ^ A D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 31

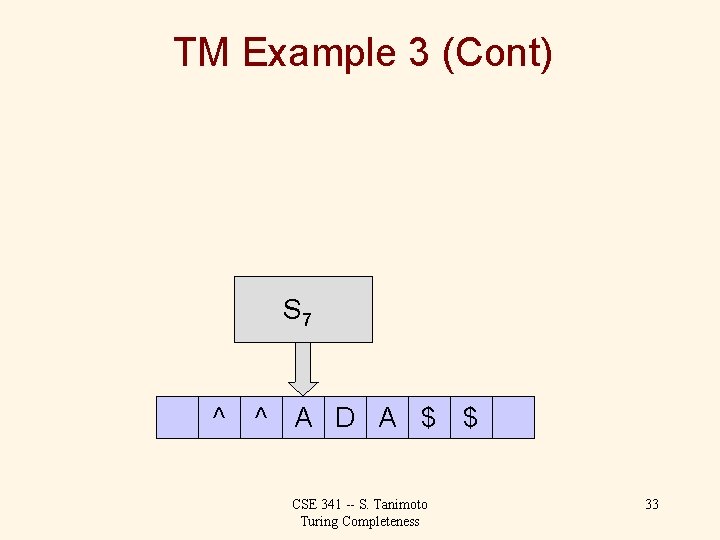
TM Example 3 (Cont) S 7 ^ ^ A D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 32

TM Example 3 (Cont) S 7 ^ ^ A D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 33

TM Example 3 (Cont) S 7 ^ ^ A D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 34

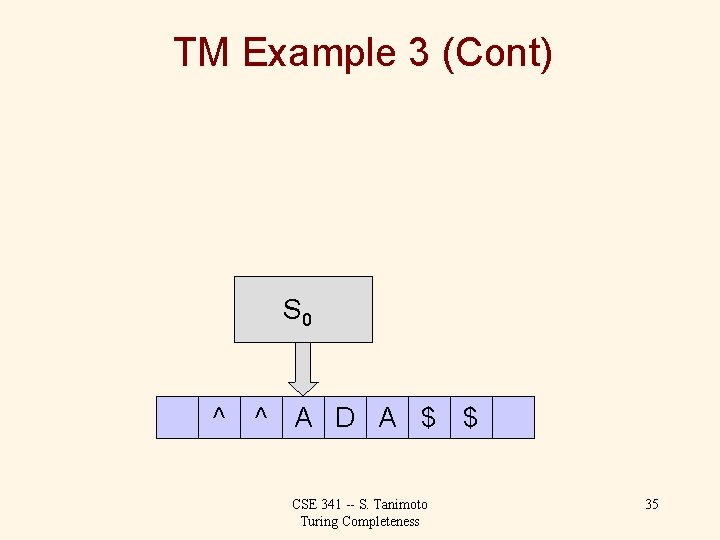
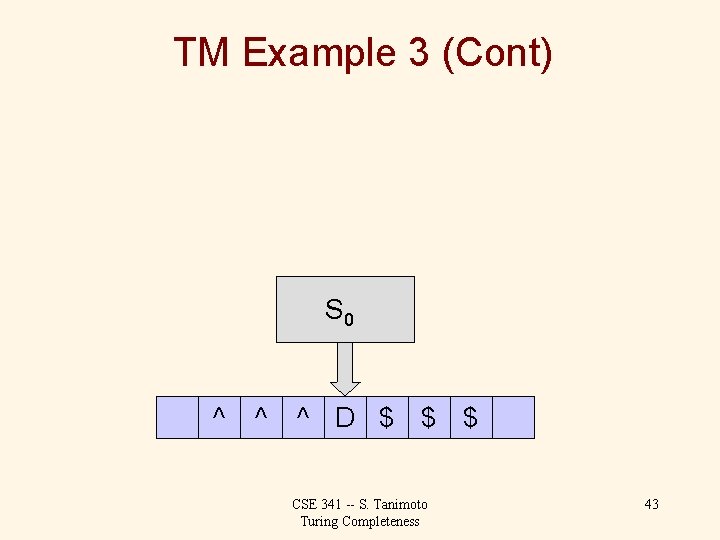
TM Example 3 (Cont) S 0 ^ ^ A D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 35

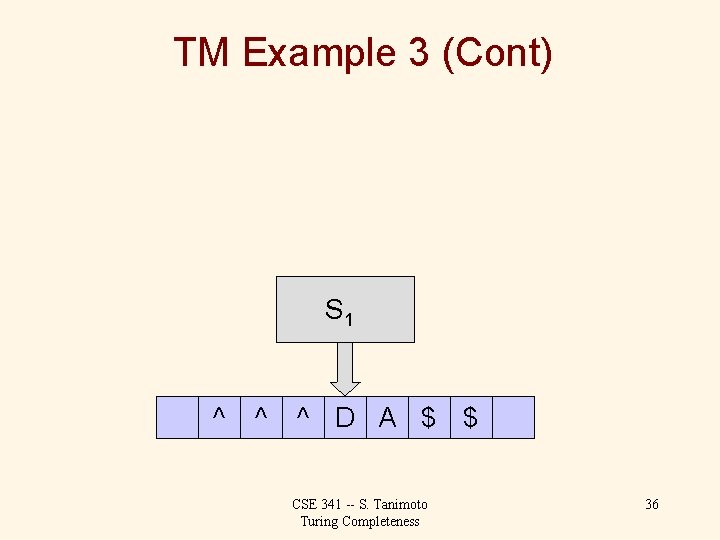
TM Example 3 (Cont) S 1 ^ ^ ^ D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 36

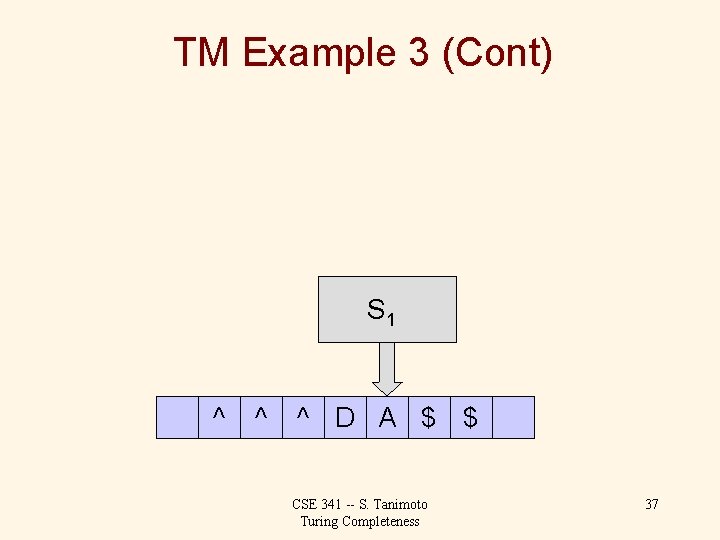
TM Example 3 (Cont) S 1 ^ ^ ^ D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 37

TM Example 3 (Cont) S 1 ^ ^ ^ D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 38

TM Example 3 (Cont) S 1 ^ ^ ^ D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 39

TM Example 3 (Cont) S 4 ^ ^ ^ D A $ $ CSE 341 -- S. Tanimoto Turing Completeness 40

TM Example 3 (Cont) S 7 ^ ^ ^ D $ $ $ CSE 341 -- S. Tanimoto Turing Completeness 41

TM Example 3 (Cont) S 7 ^ ^ ^ D $ $ $ CSE 341 -- S. Tanimoto Turing Completeness 42

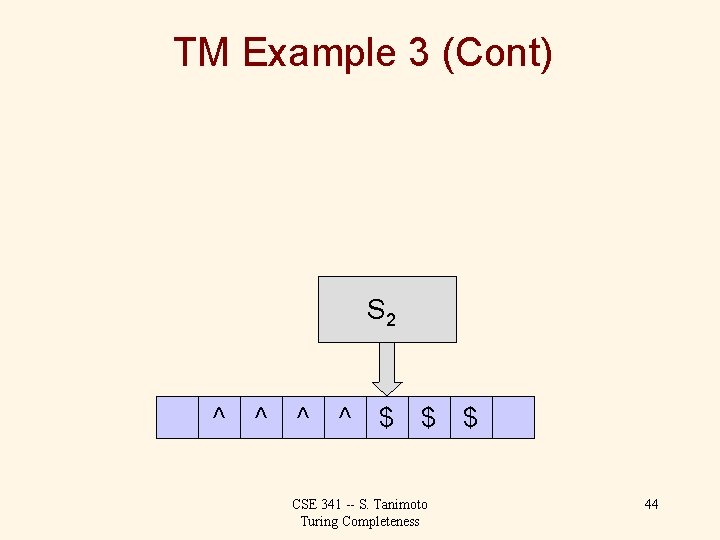
TM Example 3 (Cont) S 0 ^ ^ ^ D $ $ $ CSE 341 -- S. Tanimoto Turing Completeness 43

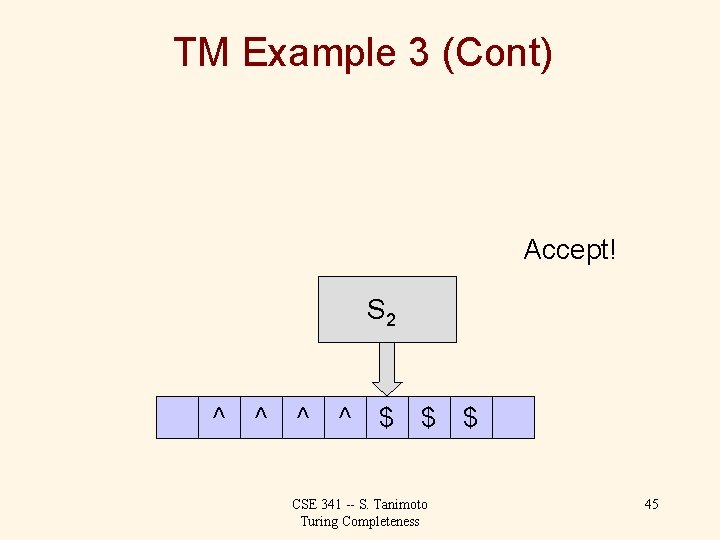
TM Example 3 (Cont) S 2 ^ ^ $ $ $ CSE 341 -- S. Tanimoto Turing Completeness 44

TM Example 3 (Cont) Accept! S 2 ^ ^ $ $ $ CSE 341 -- S. Tanimoto Turing Completeness 45

Formal Definition A Turing Machine is a 3 -tuple, T = { , , }, where is a finite set of states, is a finite tape alphabet, and is a transition function that specifies, for each and , a new tape symbol ', a new state ', and an action (one of Left, Right, Halt, Accept, or Reject). CSE 341 -- S. Tanimoto Turing Completeness 46

CSE 341 -- S. Tanimoto Turing Completeness 47

Turing Completeness A programming language L is said to be Turing complete provided that any function that can be computed by some Turing machine can also be computed by some program expressed in L. CSE 341 -- S. Tanimoto Turing Completeness 48

Applying Turing Completeness In order to show that a language is Turing complete, it suffices to show that the language provides: 1. a way to represent the current state of a TM computation, no matter how many states the TM may have, 2. a way to represent an a tape of whatever size may be needed by the computation, and to represent on each square of the tape, any tape symbol from a finite set (no matter how many symbols may be in TM’s finite set), 3. a way to implement any TM’s transition function, and 4. a way to repeat the execution of the transition function without limit. CSE 341 -- S. Tanimoto Turing Completeness 49

Applying Turing Completeness (Cont) 1. a way to represent the current state of a TM computation, no matter how many states the TM may have: An integer variable. If there are n states in , then the variable must be able to handle any number in the range {0, …, n-1}. (For large numbers of states, we could use several integer variables. In principle we may need either one “bignum” or an arbitrary finite number of fixed -precision integer variables. ) CSE 341 -- S. Tanimoto Turing Completeness 50

Applying Turing Completeness (Cont) 2. a way to represent an a tape of whatever size may be needed by the computation, and to represent on each square of the tape, any tape symbol from a finite set (no matter how many symbols may be in TM’s finite set): a dynamically growable array or a linked-list construction capability. Each element of the array or list must be able to represent an integer in the range {0, …, m-1} where m is the size of . It must be possible to read and write any element of the array or list and to simulate moving the tape head left or right. CSE 341 -- S. Tanimoto Turing Completeness 51

Applying Turing Completeness (Cont) 2. (cont) There must also be a way to keep track of the current tape head position. This could be done with a “bignum” or using a pointer if the tape is represented by a linked list. If the tape is represented by an actual serial I/O device (a real magnetic tape), then the position may be implicit and not require a program variable at all. CSE 341 -- S. Tanimoto Turing Completeness 52

Applying Turing Completeness (Cont) 3. a way to implement any TM’s transition function: Either: nestable conditionals (IF constructs) or conditionals with compound conditions, and the ability to compare the current state with an arbitrary state, and compare the current tape symbol with an arbitrary symbol. Changing the state would presumably be done by assignment, but there may be other ways of doing it (e. g. , creating new bindings in an ML style). CSE 341 -- S. Tanimoto Turing Completeness 53

Applying Turing Completeness (Cont) 4. a way to repeat the execution of the transition function without limit: Either a means of explicit looping, a means of recursion, or an implicit repetition mechanism, as in some simulation systems such as cellular automata or microworlds like Stagecast Creator. CSE 341 -- S. Tanimoto Turing Completeness 54

Turing Completeness Most real programming languages are Turing complete. If a language is not Turing complete, it may or may not qualify as a “programming language. ” However, “programming language” is a subjective term. CSE 341 -- S. Tanimoto Turing Completeness 55