Tuning SATcheckers for Bounded ModelChecking A bounded guided

Tuning SAT-checkers for Bounded Model-Checking A bounded guided tour Ofer Shtrichman Weizmann Institute & IBM-HRL Weizmann Institute

Basic theory of Bounded Model Checking (BMC( SAT highlights Tuning SAT checkers for BMC Results Weizmann Institute

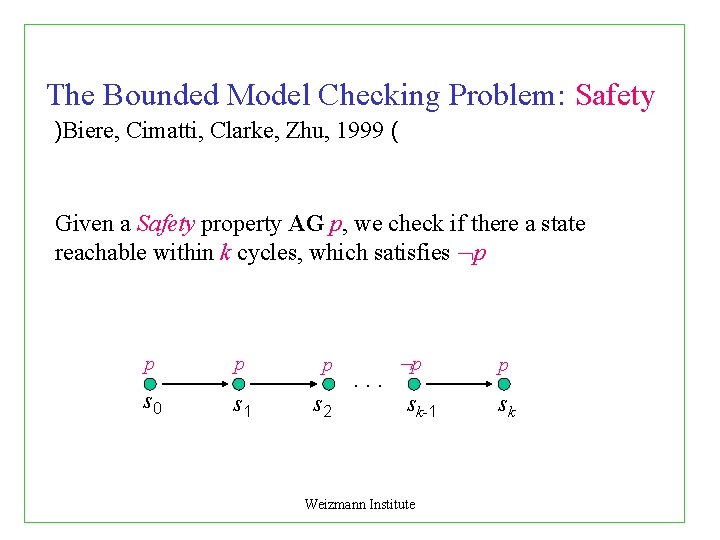
The Bounded Model Checking Problem: Safety )Biere, Cimatti, Clarke, Zhu, 1999 ( Given a Safety property AG p, we check if there a state reachable within k cycles, which satisfies p p p s 0 s 1 p s 2 . . . p sk-1 Weizmann Institute p sk

Reducing the BMC problem to SAT: p is preserved up to cycle k iff is unsatisfiable : p p s 0 s 1 p s 2 . . . p sk-1 Weizmann Institute p sk

Example: a two bit counter 00 11 01 10 p = AG ( l r. ( k =2 For k = 2, is unsatisfiabe. For k = 4 is satisfiable Weizmann Institute

Why SAT? • Smart DFS search - potentially will get faster to a satisfying sequence (counter example( • No exponential space - growth “Satisfiability checking is a ‘luck-based technology”’ Weizmann Institute

Tuning SAT for BMC (1/3( 1. Use the variable dependency graph for smarter orderings. . 2 Exploit information on ’s structure to restrict the state-space. . 3 Restrict Decide() to a small set of variables. Weizmann Institute

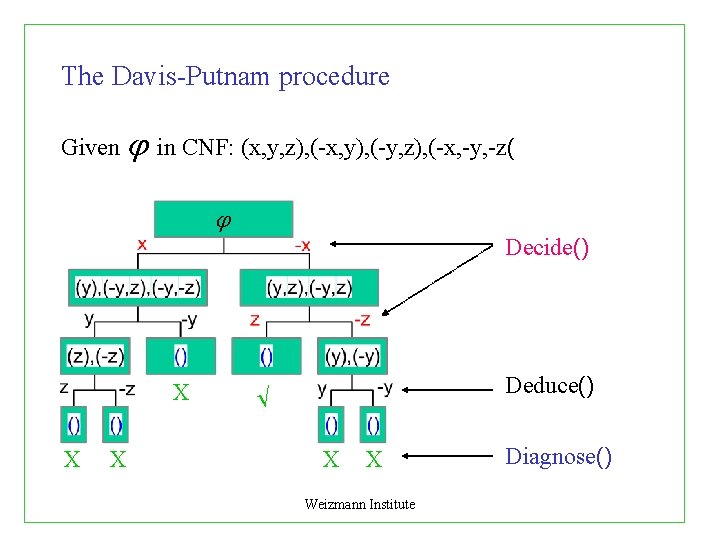
The Davis-Putnam procedure Given in CNF: (x, y, z), (-x, y), (-y, z), (-x, -y, -z( Decide() X X X Deduce() X X Weizmann Institute Diagnose()

Decide() criteria: On which variable to split? - satisfies the most clauses (DLIS) - satisfies the shortest clause - only positive or negative (‘pure literal rule’) - most frequent : : Weizmann Institute

The local effect of assignments. 1 A ‘chain reaction’ in neighboring variables, due to: Strong (1)unit clauses in Deduce() )x, y) Weak x=F y=T (2)the decision criteria in Decide() )x, y, z ( )x, y, u( x=F y = T satisfies two clauses . 2 AGp: Each clause in contains variables from max. 2 cycles. Weizmann Institute

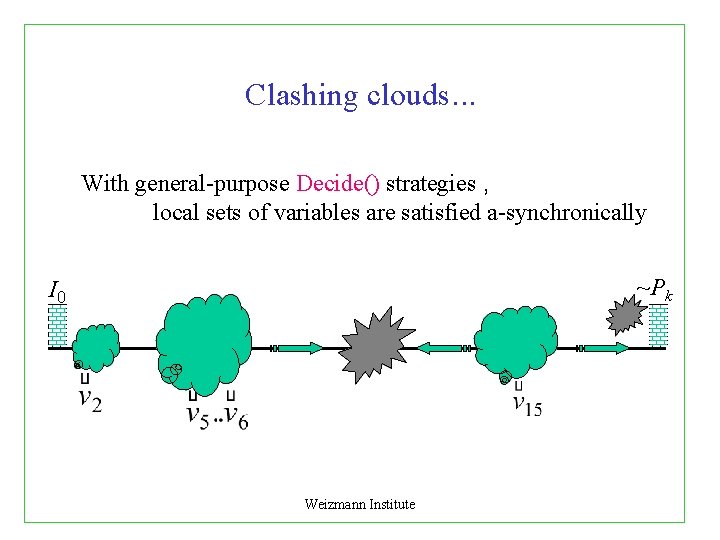
Clashing clouds. . . With general-purpose Decide() strategies , local sets of variables are satisfied a-synchronically ~Pk I 0 Weizmann Institute

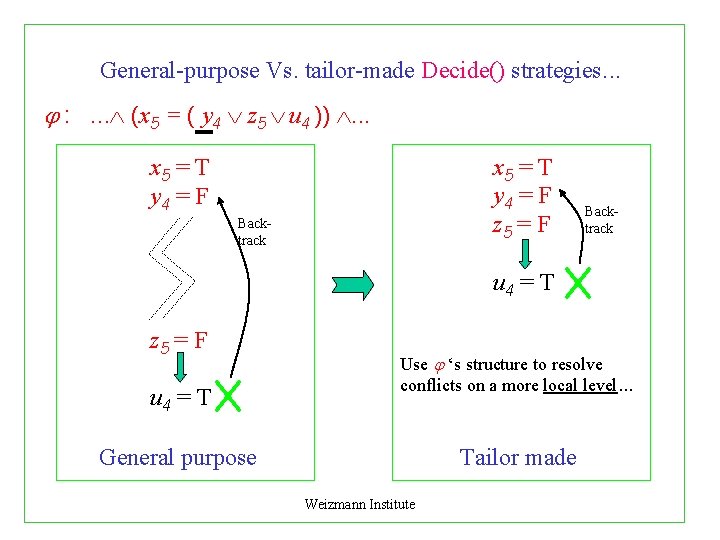
General-purpose Vs. tailor-made Decide() strategies. . . : . . . (x 5 = ( y 4 z 5 u 4 )) . . . x 5 = T y 4 = F z 5 = F x 5 = T y 4 = F Backtrack u 4 = T z 5 = F u 4 = T Use ‘s structure to resolve conflicts on a more local level. . . General purpose Tailor made Weizmann Institute

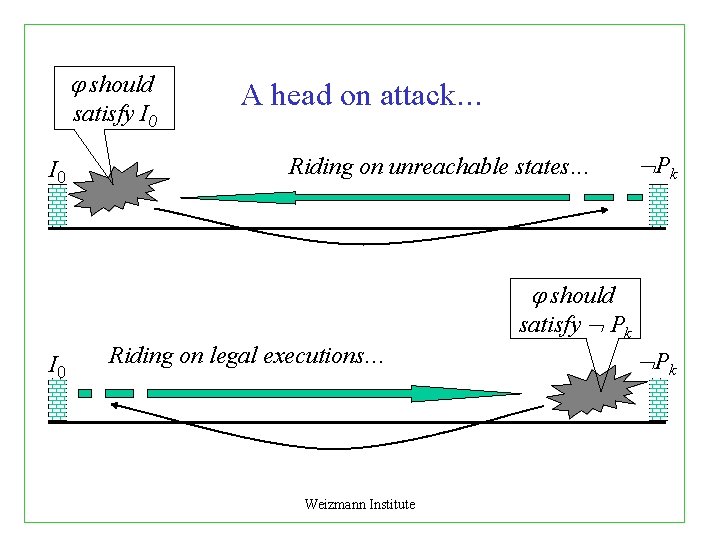
should satisfy I 0 A head on attack. . . Riding on unreachable states. . . Pk should satisfy Pk I 0 Riding on legal executions. . . Weizmann Institute Pk

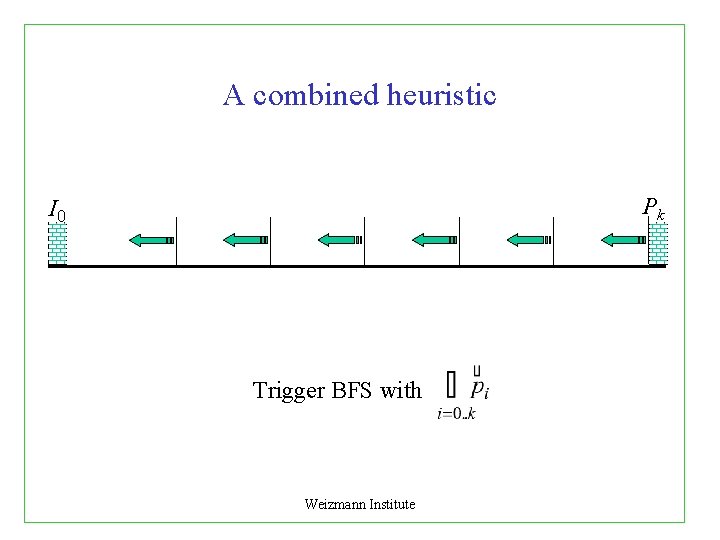
A combined heuristic Pk I 0 Trigger BFS with Weizmann Institute

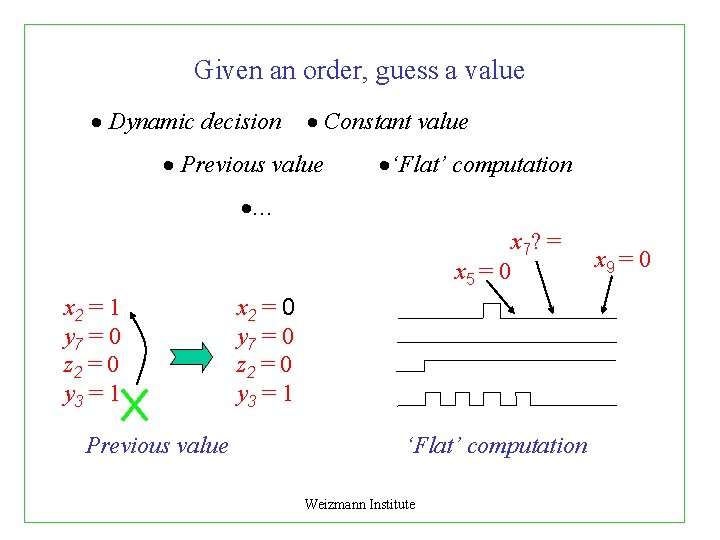
Given an order, guess a value Dynamic decision Constant value Previous value ‘Flat’ computation . . . x 5 = 0 x 2 = 1 y 7 = 0 z 2 = 0 y 3 = 1 Previous value x 7? = x 2 = 0 y 7 = 0 z 2 = 0 y 3 = 1 ‘Flat’ computation Weizmann Institute x 9 = 0

Tuning SAT for BMC (2/3( 1. Use the variable dependency graph for smarter orderings. . 2 Exploit information on ’s structure to restrict the state-space. . 3 Restrict Decide() to a small set of variables. Weizmann Institute

Exploiting ’s structure in AGp formulas ’s structure can be used for adding conflicting clauses: • If x 3=T, y 7 = F, z 5 = T leads to a conflict , then ( x 3 y 7 z 5) is satisfiable iff is satisfiable. • The new clause can be seen as a constraint on the search-space Weizmann Institute

Exploiting ’s structure in AGp formulas • If x 3=T, y 7 = F, z 5 = T leads to a conflict, then so will x 2=T, y 6 = F, z 4 = T • Therefore, we can also add : ) x 2 y 6 z 4) ( x 1 y 5 z 3) ( x 0 y 4 z 2( and. . . ( x 4 y 8 z 6) . . . ( xk-4 yk zk-2( • Yet, is not fully symmetric because of I 0. We first have to check, by simulating an assignment, if the replicated clause indeed leads to a conflict. Weizmann Institute

Tuning SAT for BMC (3/3( 1. Use the variable dependency graph for smarter orderings. . 2 Exploit information on ’s structure to restrict the state-space. . 3 Restrict Decide() to a small set of variables. Weizmann Institute

Restricting Decide() to a smaller set of variables , that uniquely determines the satisfiability of : Model variables (~ 15 % of ’s variables( Input variables (~ 5 % of ’s variables( Less variables to Decide() implies more variables to Deduce() Weizmann Institute

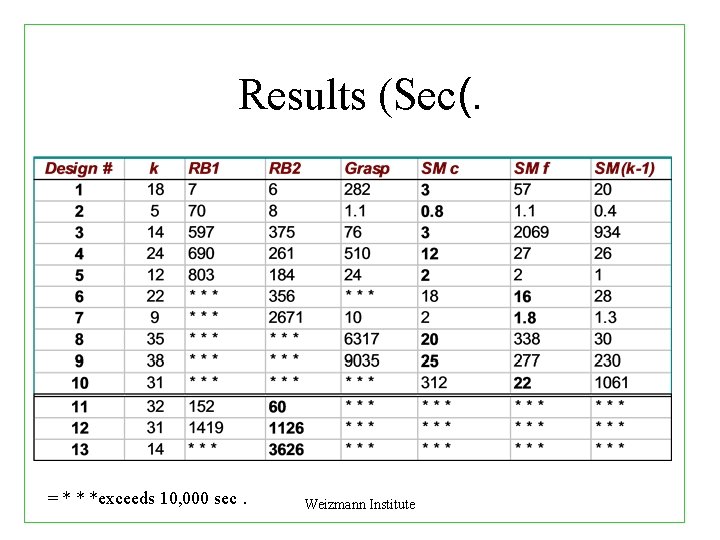
Results (Sec(. = * * *exceeds 10, 000 sec. Weizmann Institute

The Conclusion Many of the (BDD) hard cases can be more efficiently solved with the optimized SAT procedure. Weizmann Institute