Tuned Boyer Moore Algorithm Raita Algorithm Horspool Algorithm

Tuned Boyer Moore Algorithm Raita Algorithm Horspool Algorithm Quick Search Algorithm Smith Algorithm Zhu-Takaoka Algorithm Adviser: R. C. T. Lee Speaker: C. W. Cheng National Chi Nan University 1

Problem Definition Input: a text string T with length n and a pattern string P with length m. Output: all occurrences of P in T. 2

Definition • Ts : the first character of a string T aligns to a pattern P. • Pl : the first character of a pattern P aligns to a string T. • Tj : the character of the jth position of a string T. • Pi : the character of the ith position of a pattern P. • Pf : the last character of a pattern P. • n : The length of T. • m : The length of P. 3

Rule 2 -2: 1 -Suffix Rule (A Special Version of Rule 2) • Consider the 1 -suffix x. We may apply Rule 2 -2 now. 4

Tuned Boyer Moore Algorithm Fast string searching , HUME A. and SUNDAY D. M. , Software - Practice & Experience 21(11), 1991, pp. 1221 -1248. 5

Introduction • simplification of the Boyer-Moore algorithm. • uses only the bad-character shift. • easy to implement. • very fast in practice • uses Rule 2 -2: 1 -Suffix Rule 6

Tuned Boyer Moore Algorithm • In this algorithm, We always focus on the last character of the window of T and try to slide the pattern to match the last character of T. 7

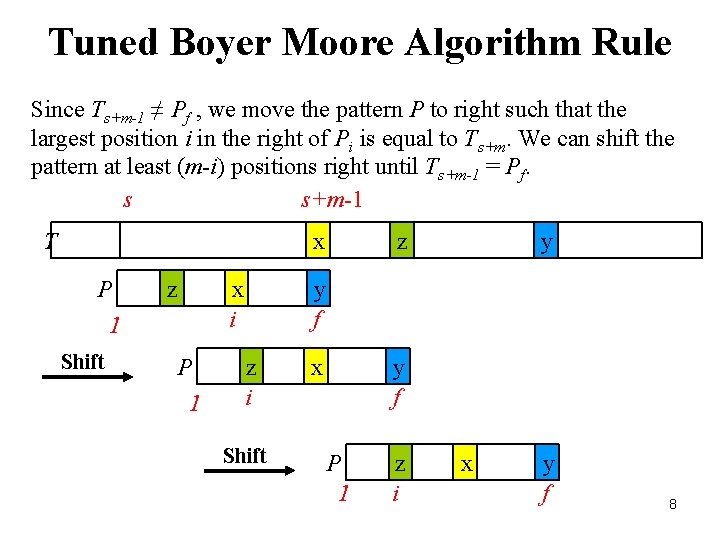
Tuned Boyer Moore Algorithm Rule Since Ts+m-1 ≠ Pf , we move the pattern P to right such that the largest position i in the right of Pi is equal to Ts+m. We can shift the pattern at least (m-i) positions right until Ts+m-1 = Pf. s s+m-1 T x P z x i 1 Shift P 1 z y y f z i Shift x y f P 1 z i x y f 8

Tuned Boyer Moore Preprocessing Table • In this algorithm, we construct a table as follow. Let x be a character in the alphabet. We record the position of the last x, if it exists in P, we record the position of x from the second last position of P. If x does not exist in P 1 to Pm-1, we record it as m. 9

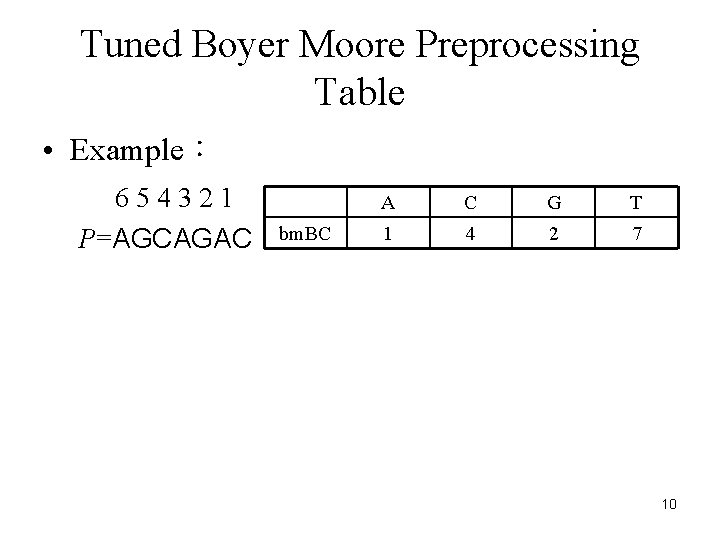
Tuned Boyer Moore Preprocessing Table • Example： 654321 P=AGCAGAC bm. BC A C G T 1 4 2 7 10

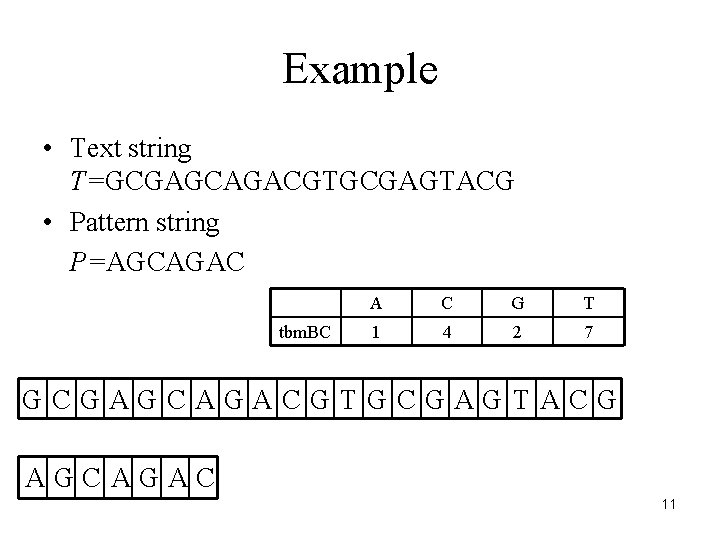
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG AGCAGAC 11

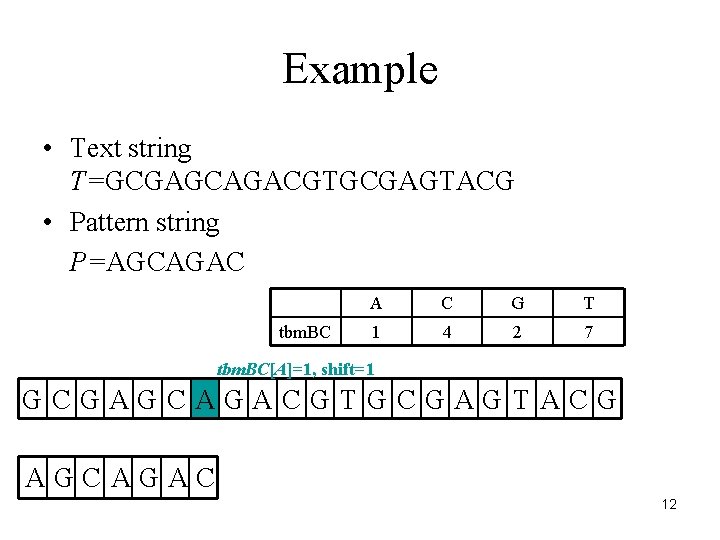
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 tbm. BC[A]=1, shift=1 GCGAGCAGACGTGCGAGTACG AGCAGAC 12

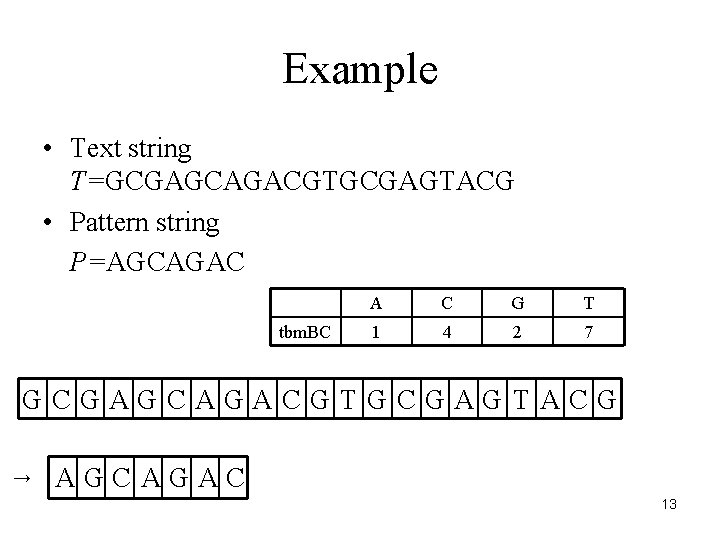
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 13

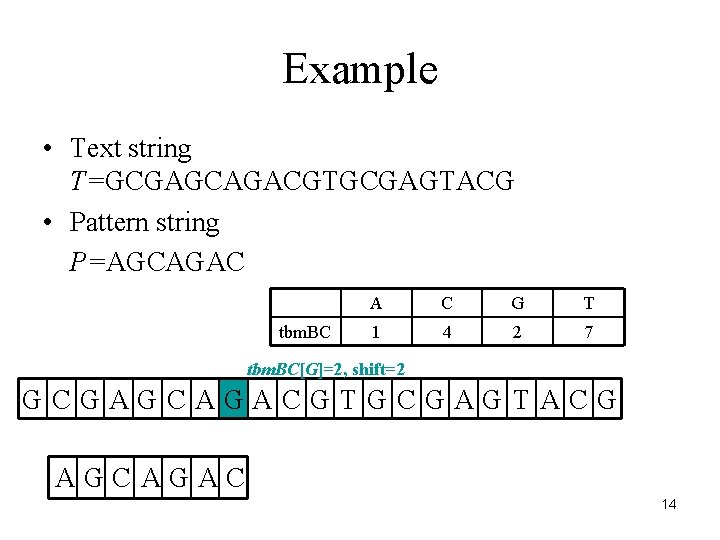
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 tbm. BC[G]=2, shift=2 GCGAGCAGACGTGCGAGTACG AGCAGAC 14

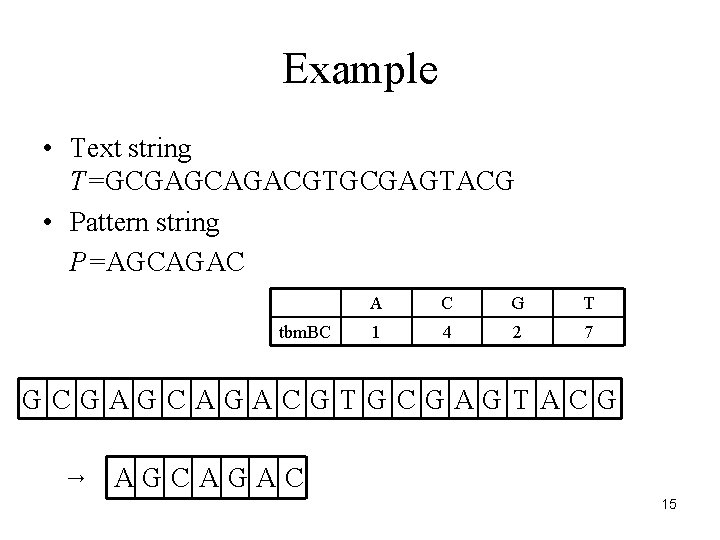
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 15

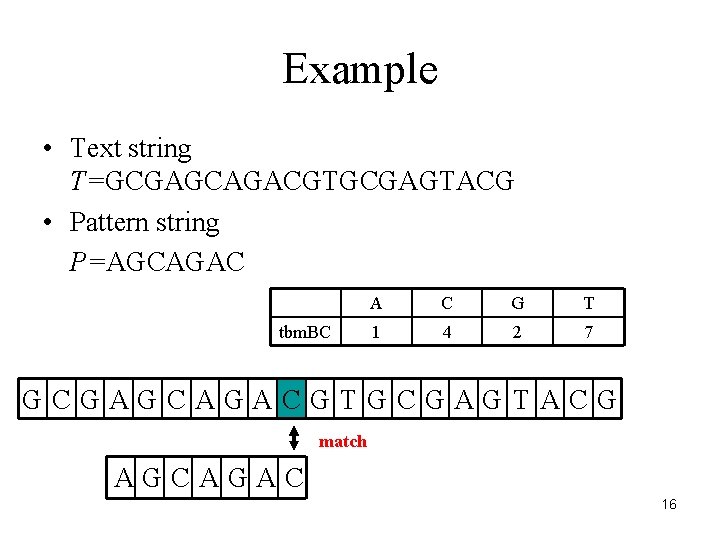
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 16

Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 tbm. BC[C]=4, shift=4 GCGAGCAGACGTGCGAGTACG exact match AGCAGAC 17

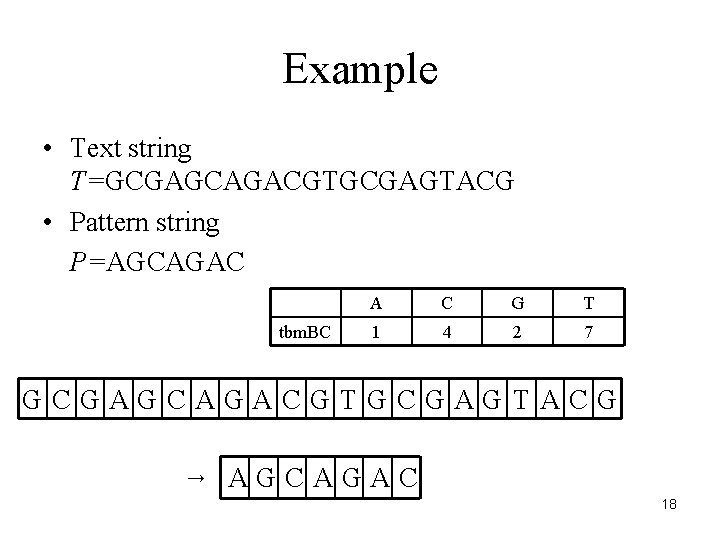
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 18

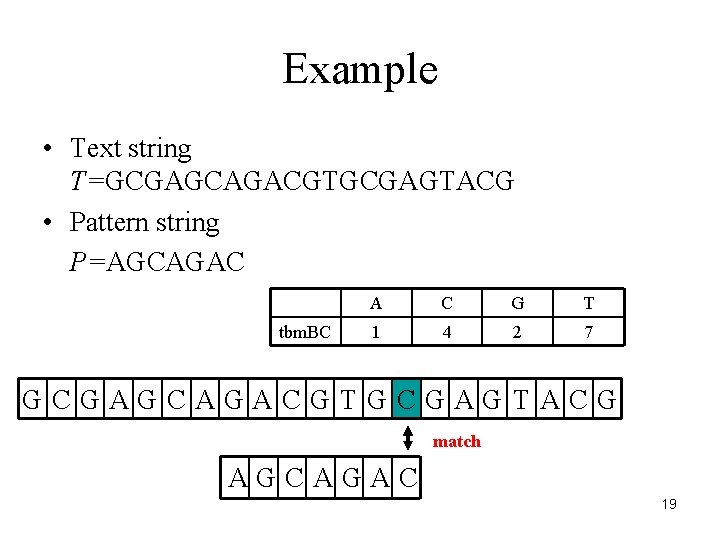
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 19

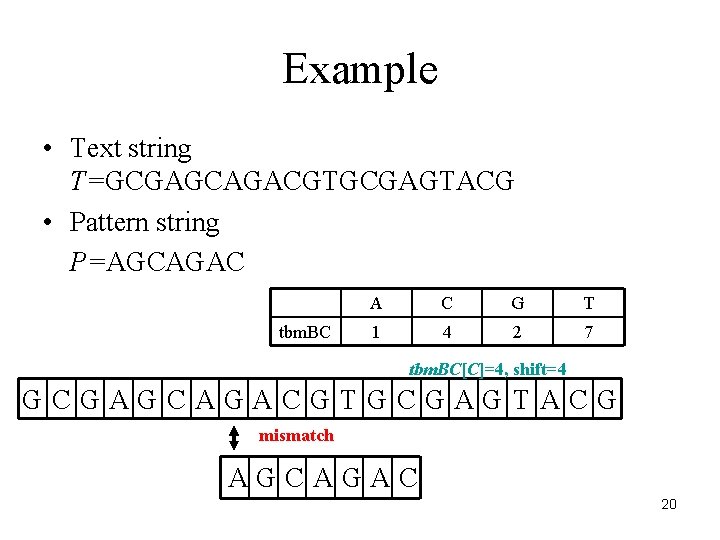
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 tbm. BC[C]=4, shift=4 GCGAGCAGACGTGCGAGTACG mismatch AGCAGAC 20

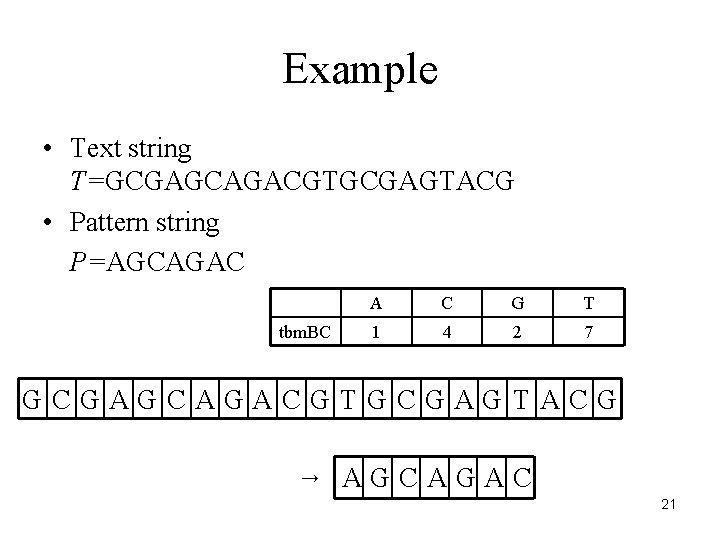
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 21

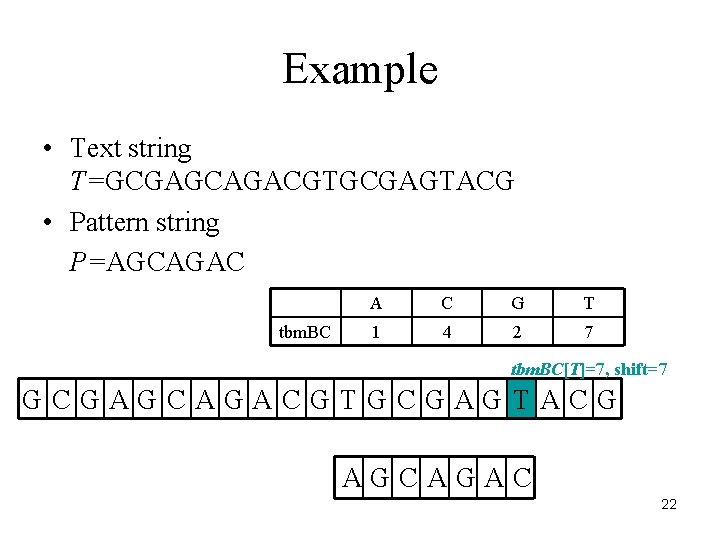
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 tbm. BC[T]=7, shift=7 GCGAGCAGACGTGCGAGTACG AGCAGAC 22

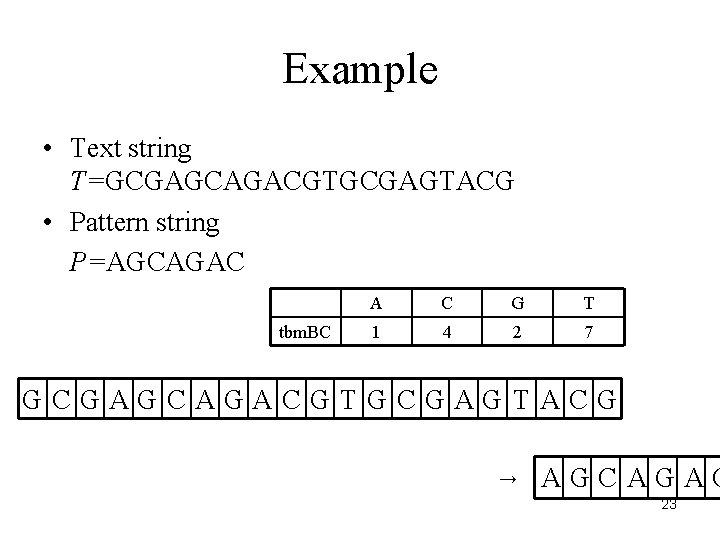
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC tbm. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 23

Time complexity • preprocessing phase in O(m+ σ) time and O(σ) space complexity, σ is the number of alphabets in pattern. • searching phase in O(mn) time complexity. 24

Raita Algorithm Tuning the Boyer-Moore-Horspool string searching algorithm, T. RAITA, Software Practice & Experience, 22(10), 1994, pp. 879 -884 25

Introduction • simplification of the Boyer-Moore algorithm. • uses only the bad-character shift. • easy to implement. • very fast in practice • uses Rule 2 -2: 1 -Suffix Rule 26

Raita Algorithm • In this algorithm, first we compare the last character of the window of T with the last character of the pattern, then we compare the first character and the middle character of the window. If they match, we compare other characters from left to right. If mismatch occurs, we slide the window by the preprocessing table. 27

Raita Preprocessing Table • The preprocessing table of Raita algorithm is the same with Tuned Boyer-Moore algorithm. 28

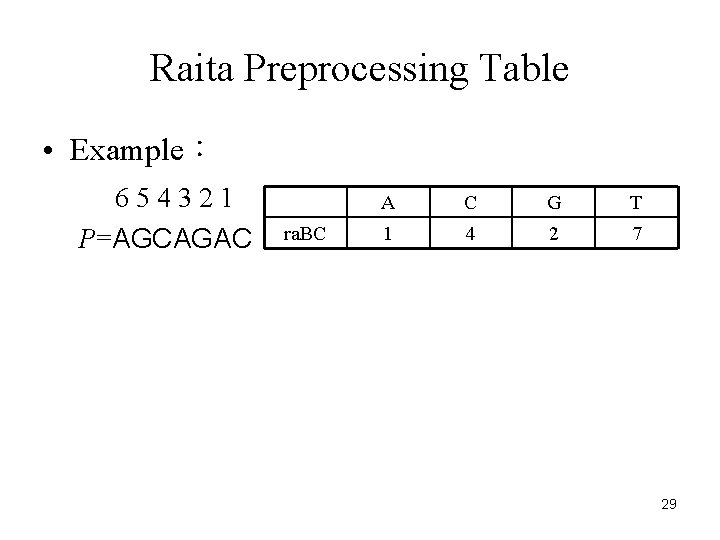
Raita Preprocessing Table • Example： 654321 P=AGCAGAC ra. BC A C G T 1 4 2 7 29

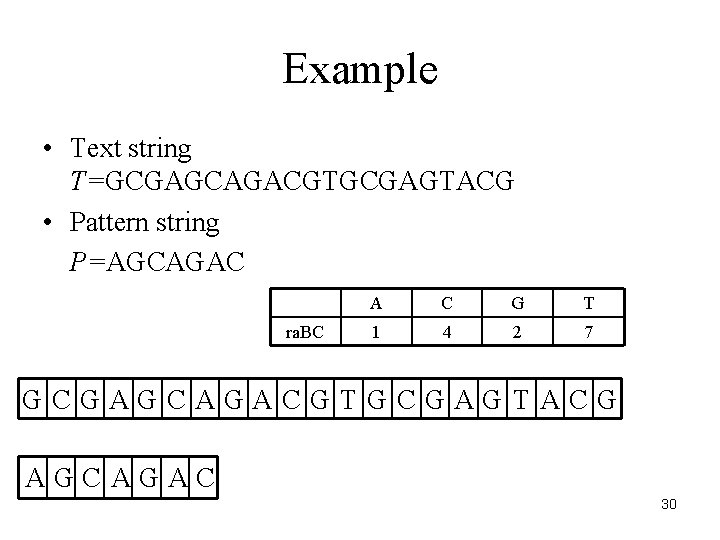
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG AGCAGAC 30

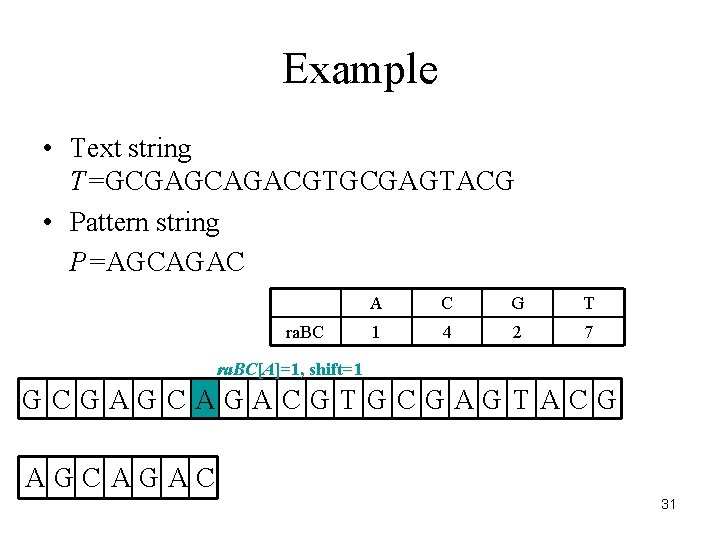
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 ra. BC[A]=1, shift=1 GCGAGCAGACGTGCGAGTACG AGCAGAC 31

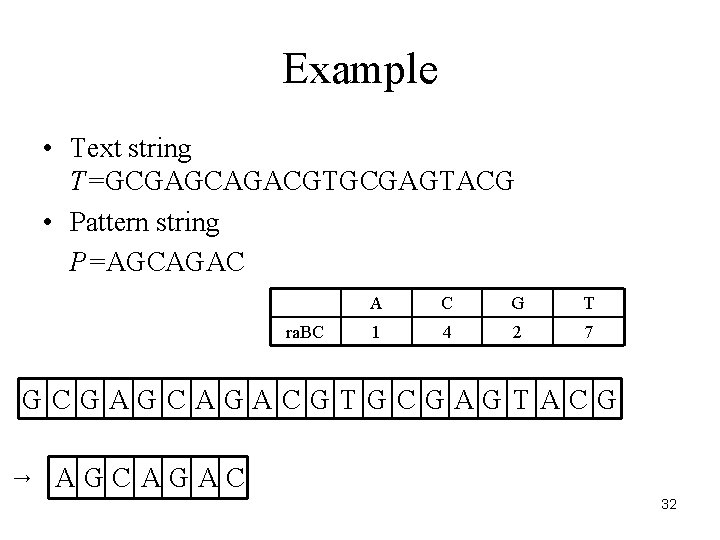
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 32

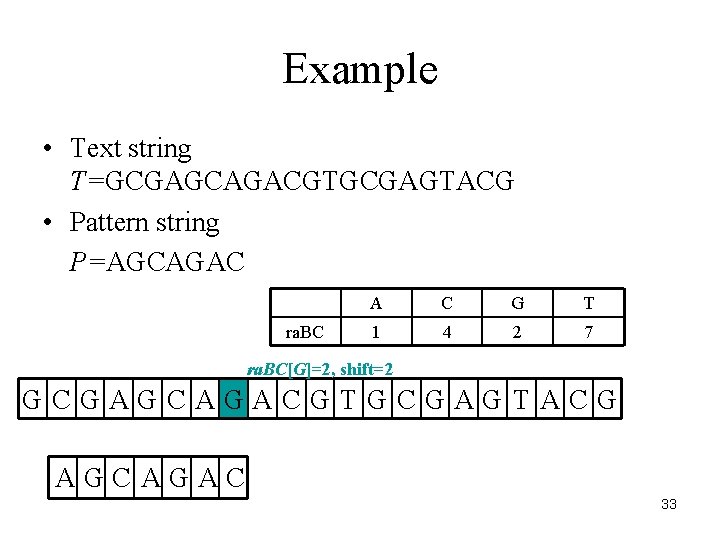
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 ra. BC[G]=2, shift=2 GCGAGCAGACGTGCGAGTACG AGCAGAC 33

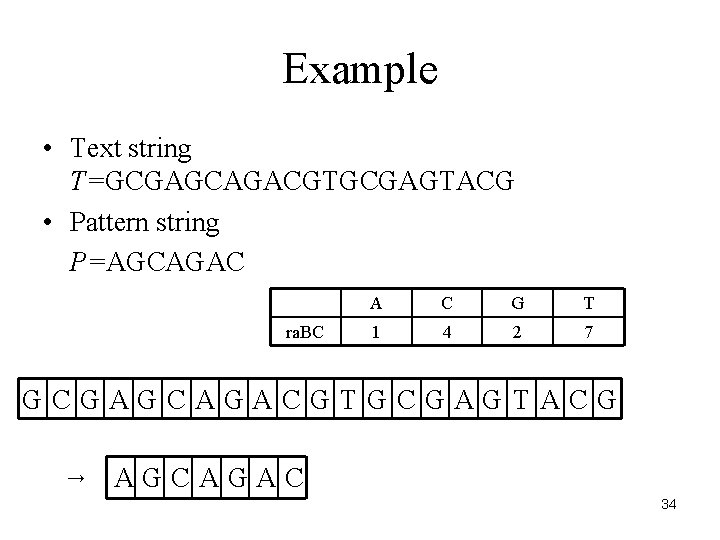
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 34

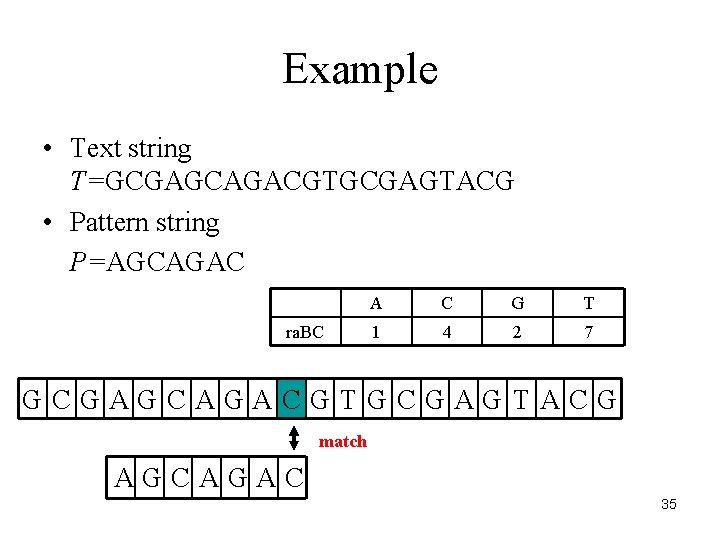
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 35

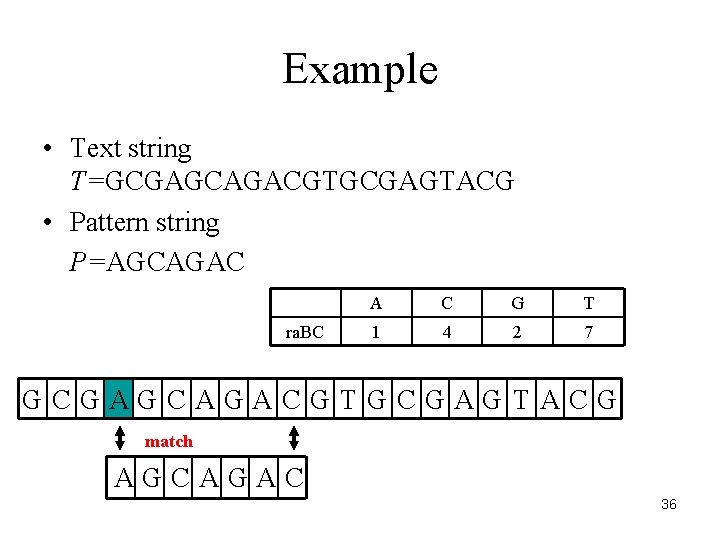
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 36

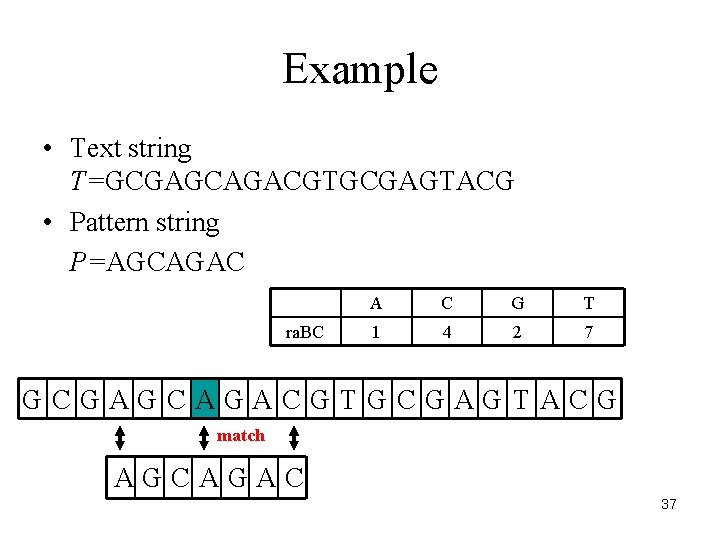
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 37

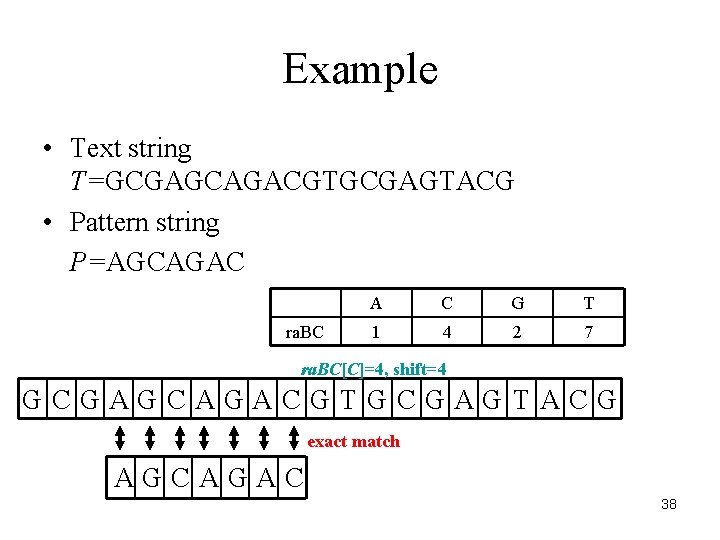
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 ra. BC[C]=4, shift=4 GCGAGCAGACGTGCGAGTACG exact match AGCAGAC 38

Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 39

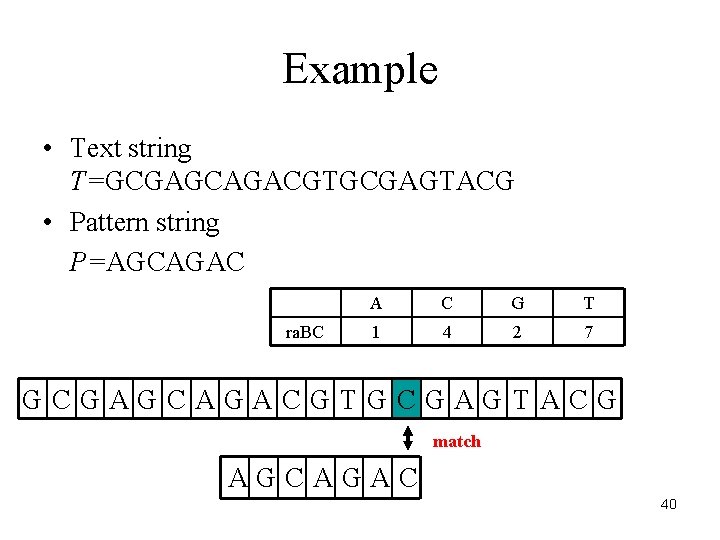
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 40

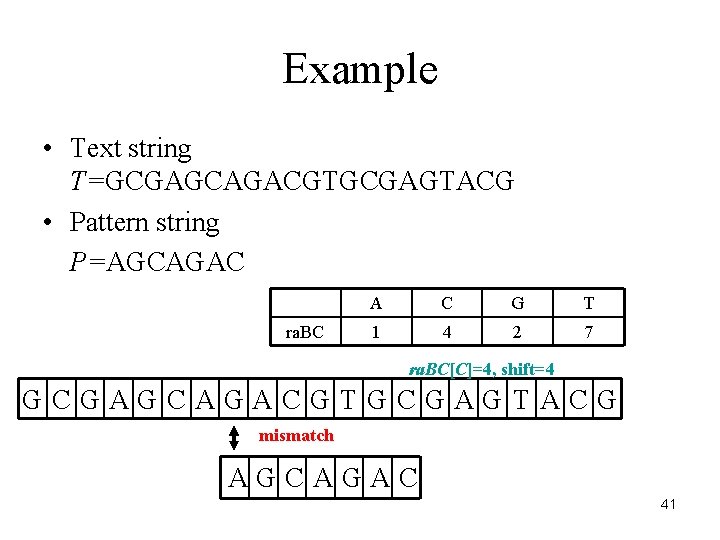
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 ra. BC[C]=4, shift=4 GCGAGCAGACGTGCGAGTACG mismatch AGCAGAC 41

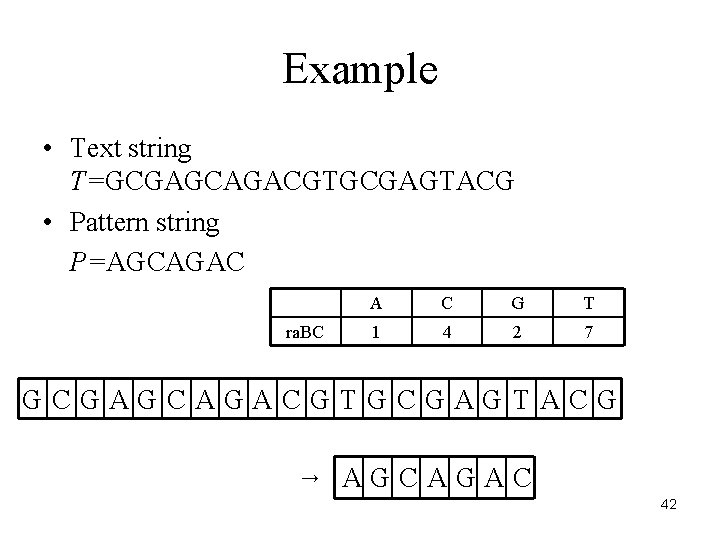
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 42

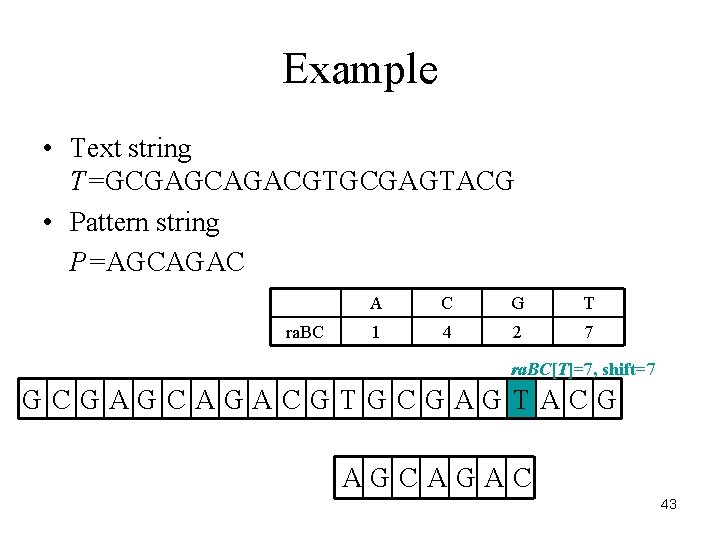
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 ra. BC[T]=7, shift=7 GCGAGCAGACGTGCGAGTACG AGCAGAC 43

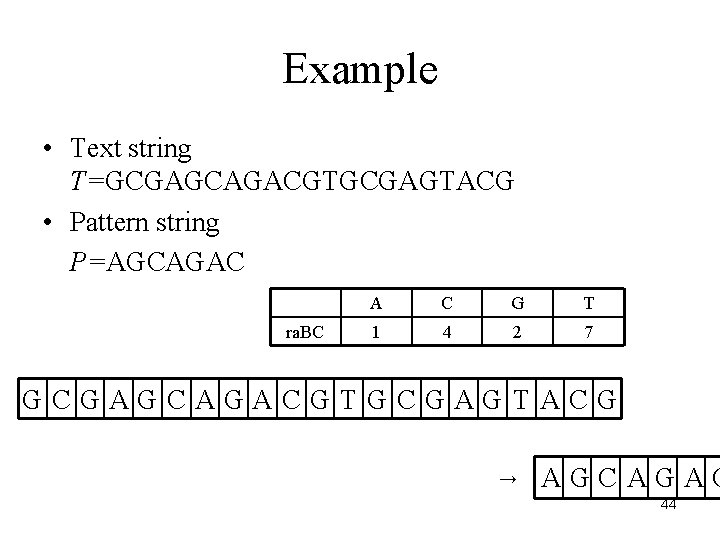
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC ra. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 44

Time complexity • preprocessing phase in O(m+ σ) time and O(σ) space complexity, σ is the number of alphabets in pattern. • searching phase in O(mn) time complexity. 45

Horspool Algorithm Practical fast searching in strings, R. NIGEL HORSPOOL, SOFTWAREPRACTICE AND EXPERIENCE, VOL. 10, 1980, pp. 501 -506 46

Introduction • simplification of the Boyer-Moore algorithm. • uses only the bad-character shift. • easy to implement. • very fast in practice • uses Rule 2 -2: 1 -Suffix Rule 47

Horspool Algorithm • In this algorithm, We always compare the window of T with pattern from right to left and try to slide the pattern to match the last character of T. 48

Horspool Preprocessing Table • The preprocessing table of Horspool algorithm is the same with Tuned Boyer-Moore algorithm. 49

Horspool Preprocessing Table • Example： 654321 P=AGCAGAC hp. BC A C G T 1 4 2 7 50

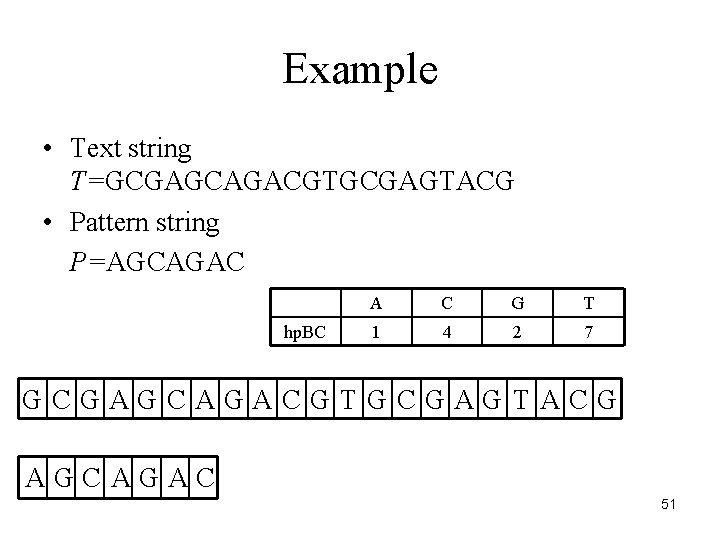
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG AGCAGAC 51

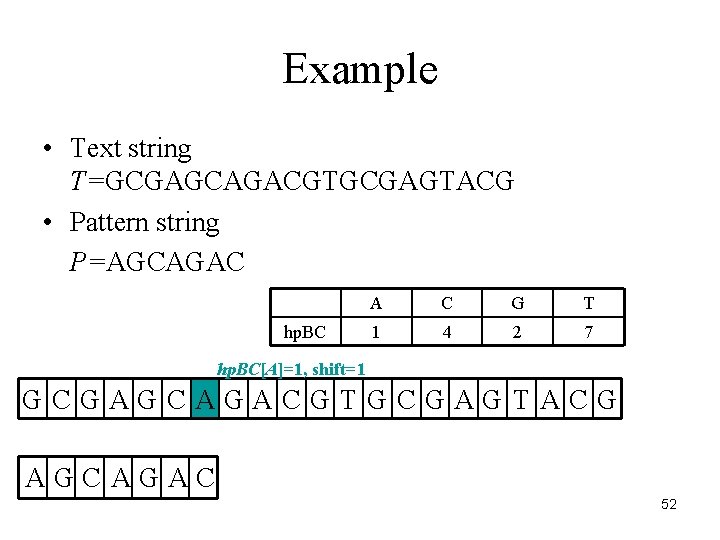
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 hp. BC[A]=1, shift=1 GCGAGCAGACGTGCGAGTACG AGCAGAC 52

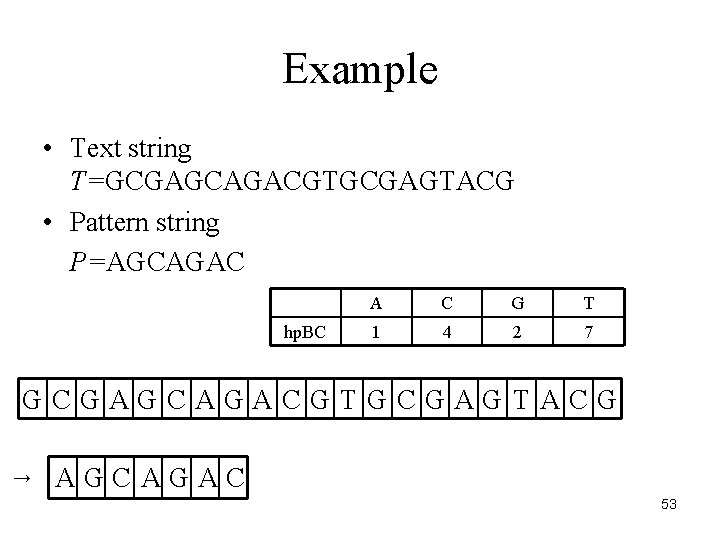
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 53

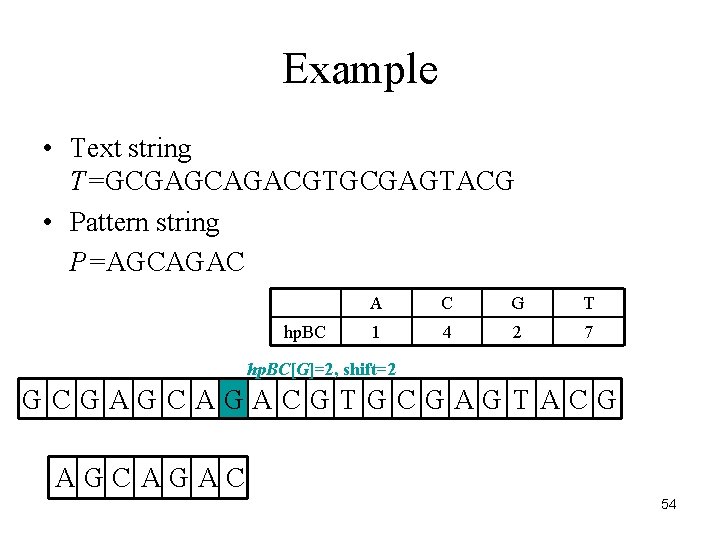
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 hp. BC[G]=2, shift=2 GCGAGCAGACGTGCGAGTACG AGCAGAC 54

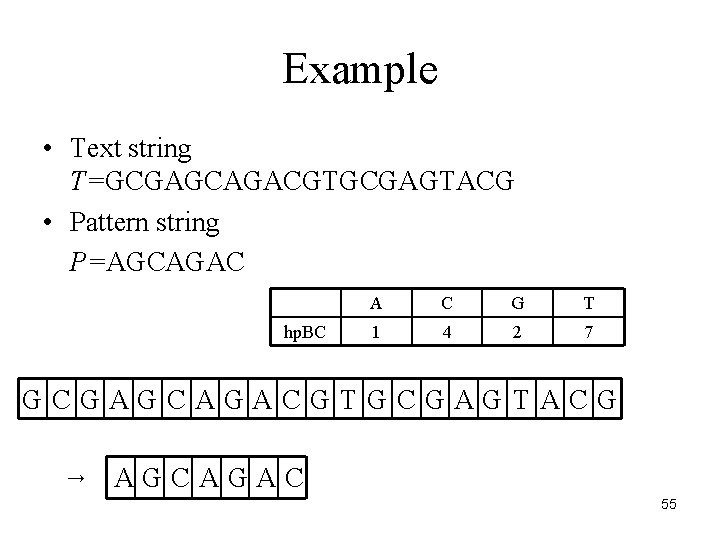
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 55

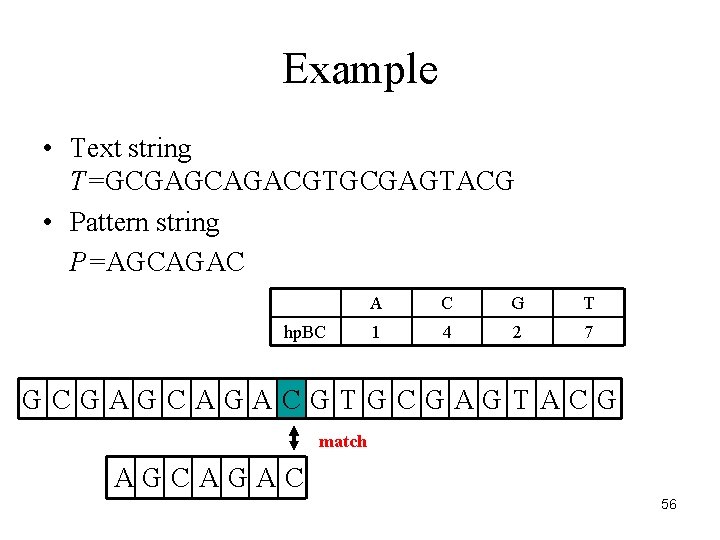
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 56

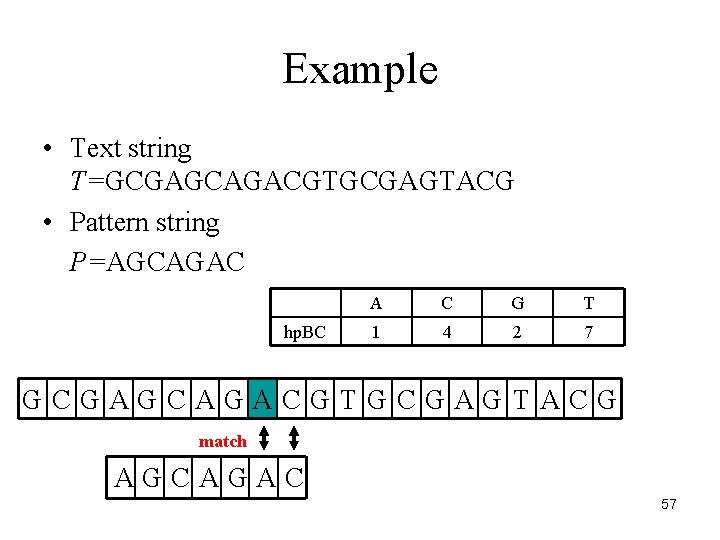
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 57

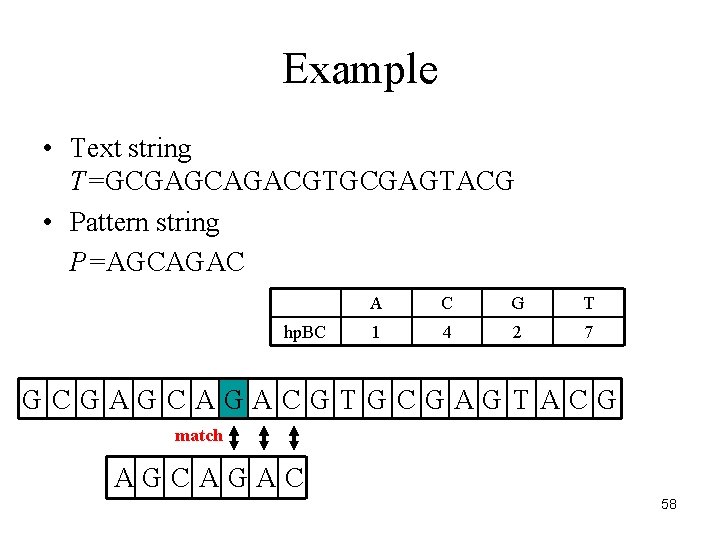
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 58

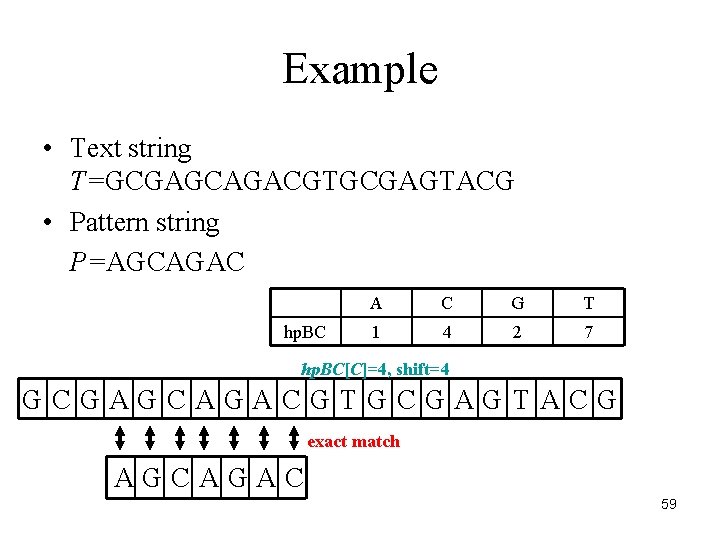
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 hp. BC[C]=4, shift=4 GCGAGCAGACGTGCGAGTACG exact match AGCAGAC 59

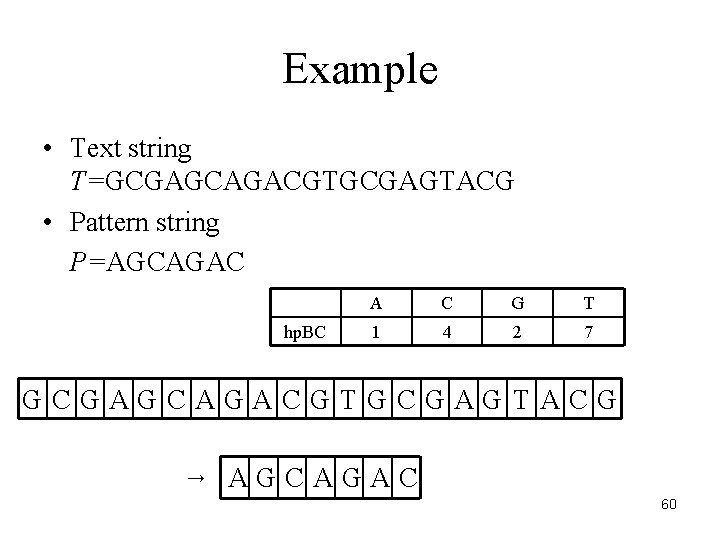
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 60

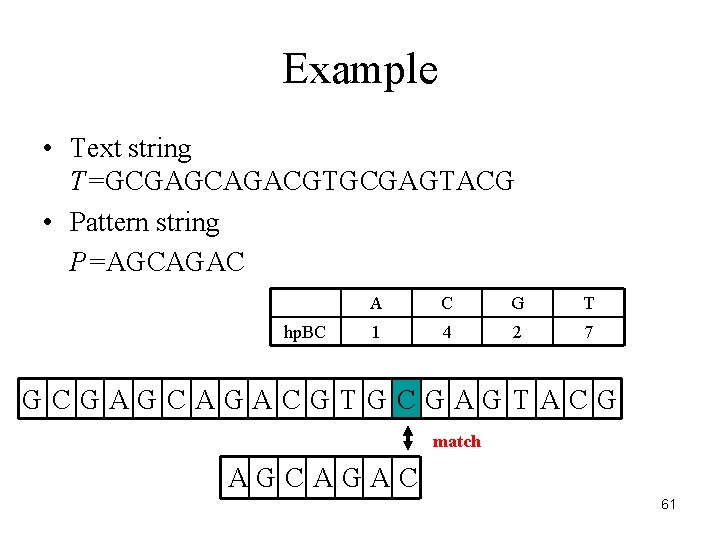
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match AGCAGAC 61

Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 hp. BC[G]=2, shift=2 GCGAGCAGACGTGCGAGTACG mismatch AGCAGAC 62

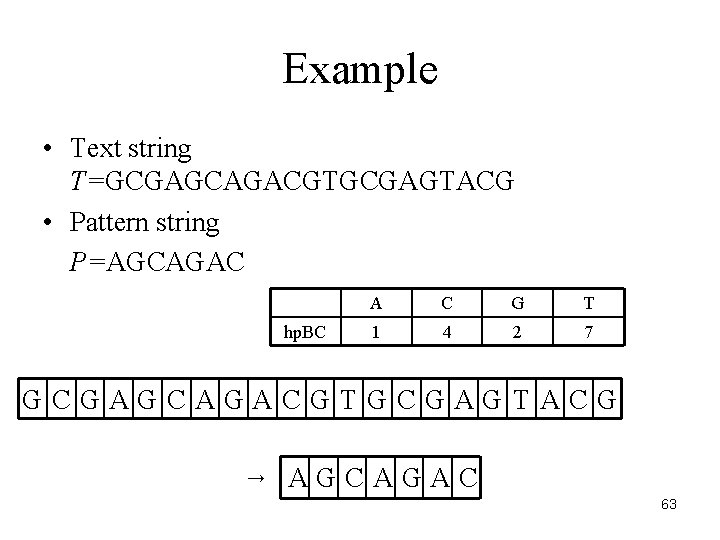
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 63

Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 hp. BC[A]=1, shift=1 GCGAGCAGACGTGCGAGTACG mismatch AGCAGAC 64

Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 65

Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 hp. BC[G]=2, shift=2 GCGAGCAGACGTGCGAGTACG mismatch → AGCAGAC 66

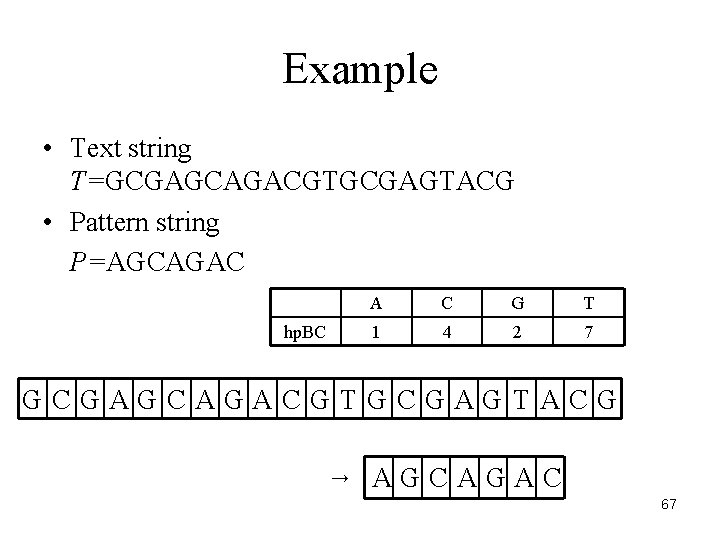
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 67

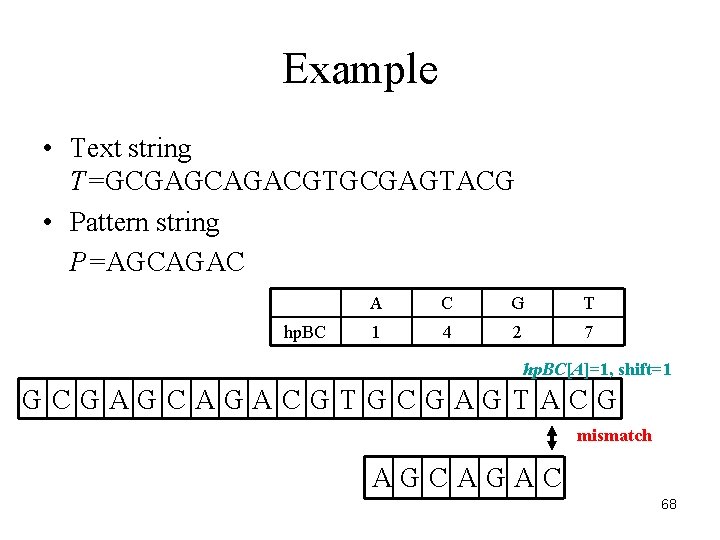
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 hp. BC[A]=1, shift=1 GCGAGCAGACGTGCGAGTACG mismatch AGCAGAC 68

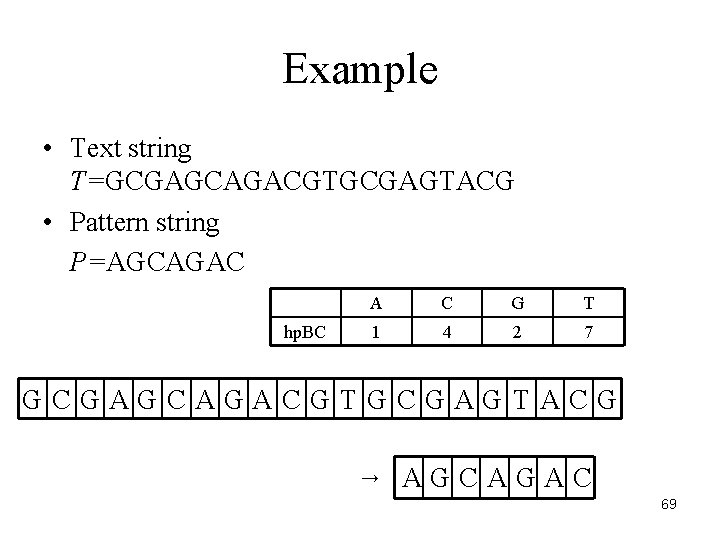
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 69

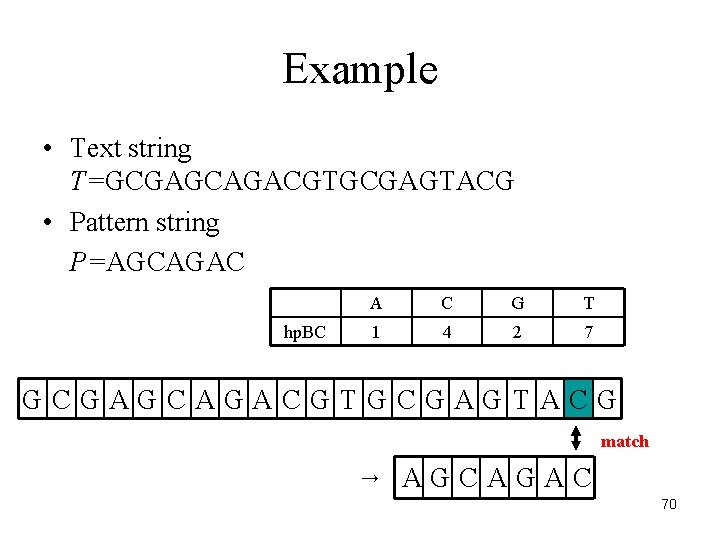
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match → AGCAGAC 70

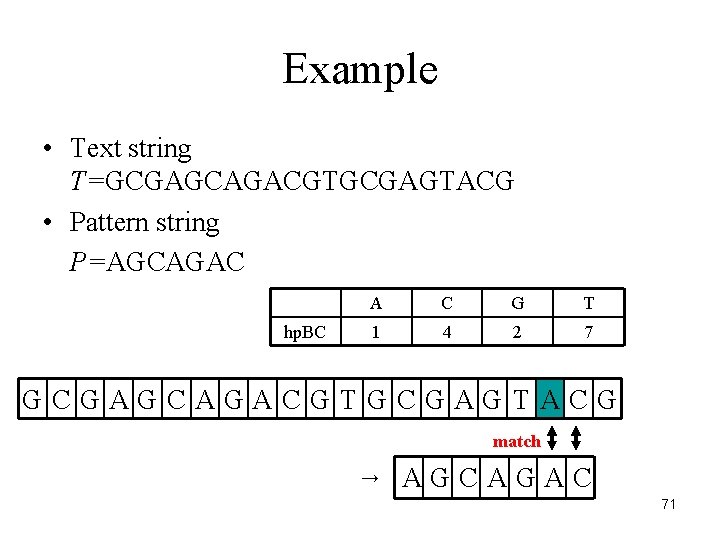
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG match → AGCAGAC 71

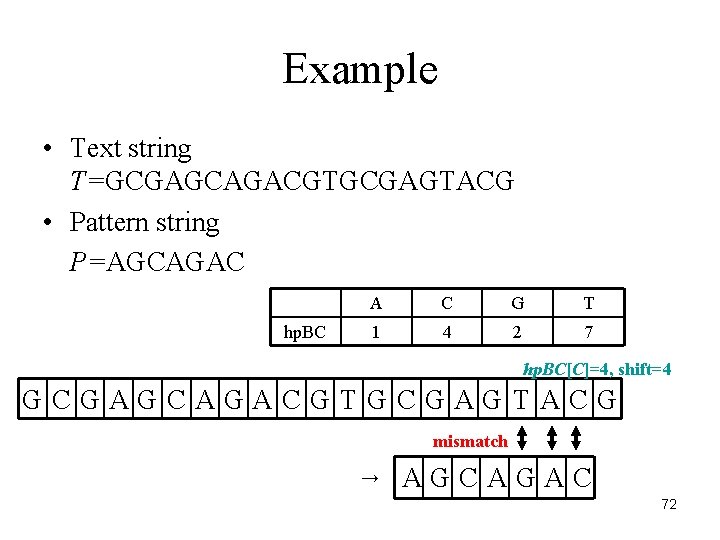
Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 hp. BC[C]=4, shift=4 GCGAGCAGACGTGCGAGTACG mismatch → AGCAGAC 72

Example • Text string T=GCGAGCAGACGTGCGAGTACG • Pattern string P=AGCAGAC hp. BC A C G T 1 4 2 7 GCGAGCAGACGTGCGAGTACG → AGCAGAC 73

Time complexity • preprocessing phase in O(m+ σ) time and O(σ) space complexity, σ is the number of alphabets in pattern. • searching phase in O(mn) time complexity. 74

Quick Search Algorithm A very fast substring search algorithm, SUNDAY D. M. , Communications of the ACM. 33(8), 1990, pp. 132 -142. 75

Introduction • simplification of the Boyer-Moore algorithm. • uses only the bad-character shift. • easy to implement. • uses Rule 2 -2: 1 -Suffix Rule 76

Quick Search Rule Suppose that P 1 is aligned to Ts now, and we perform a pairwise comparing between text T and pattern P from left to right. Assume that the first mismatch occurs when comparing Tq with Pp. Since Tq ≠Pp , we move the pattern P to right such that the largest position i in the right of Pi is equal to Ts+m. We can shift the pattern at least (m-i) positions right. s q s+m T t y x mismatch P t z p 1 Shift P x i t 1 z p x i 77

Quick Search Preprocessing Table • The only thing we want to do is to construct a table as follow. Let x be a character in the alphabet. We record the position of the last x, if it exists in P, we counted the position of x from the right end. If x does not exist in P, we record it as m+1. 78

Quick Search Preprocessing Table • Example： 7654321 P=CAGAGAG qs. BC A 2 C 7 G 1 T 8 • With this table, the number of steps which we move the pattern can be easily done. After the movement, we compare the pattern and the text from left to right until a mismatch occurs, otherwise we output the position of the first character in T which aligns to pattern P. 79

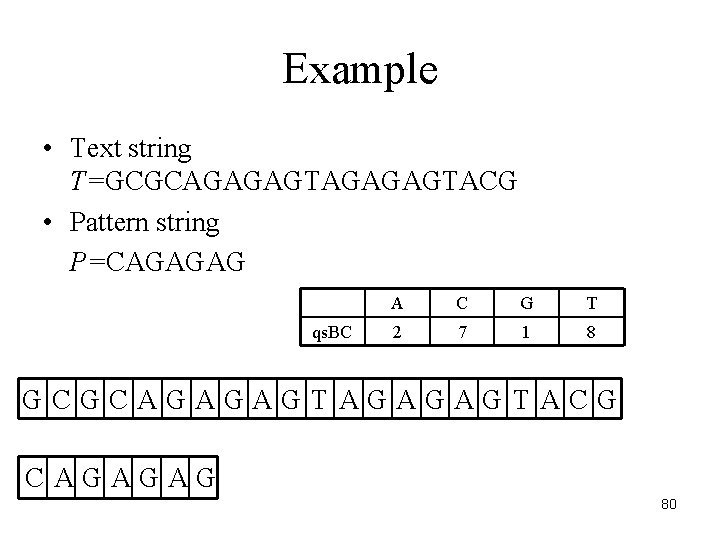
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 80

Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG mismatch CAGAGAG 81

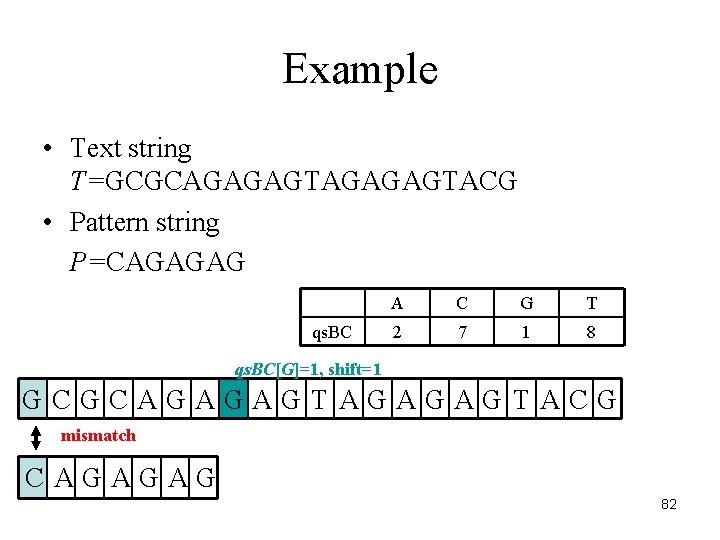
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 qs. BC[G]=1, shift=1 GCGCAGAGAGTACG mismatch CAGAGAG 82

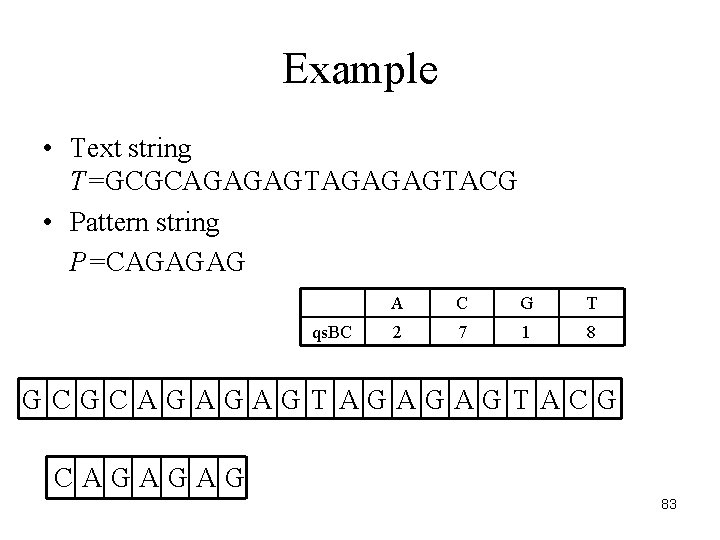
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 83

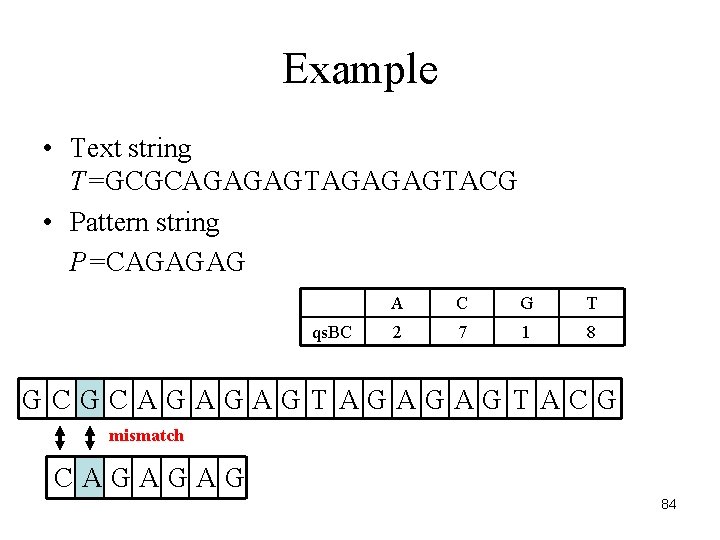
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG mismatch CAGAGAG 84

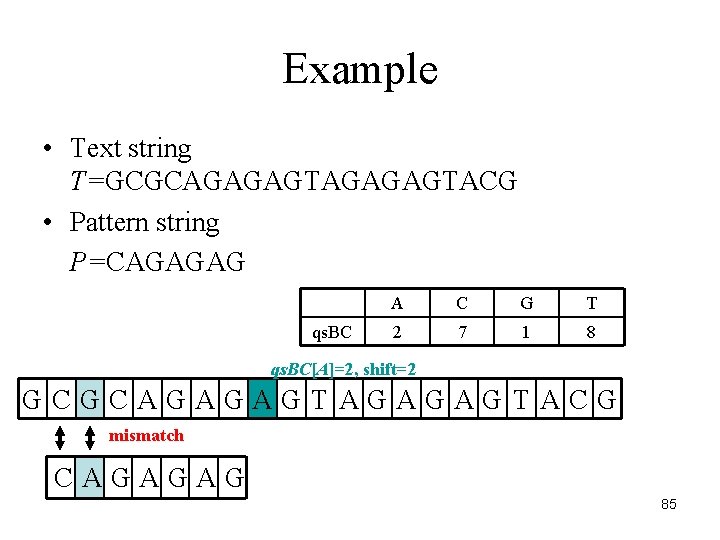
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 qs. BC[A]=2, shift=2 GCGCAGAGAGTACG mismatch CAGAGAG 85

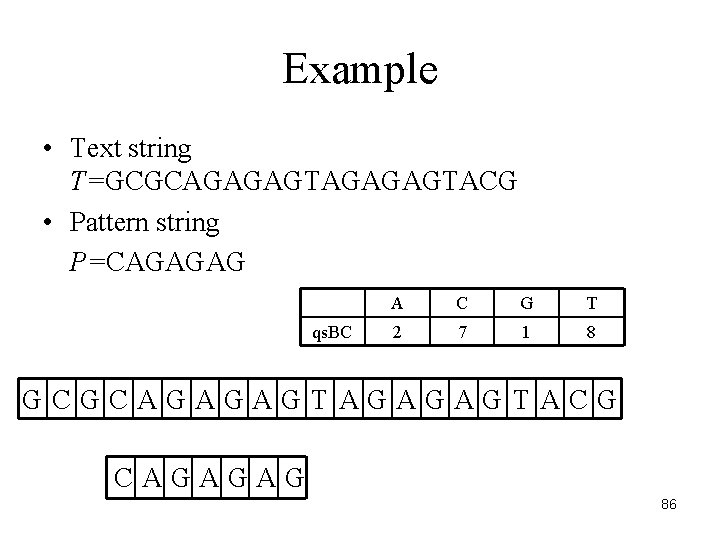
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 86

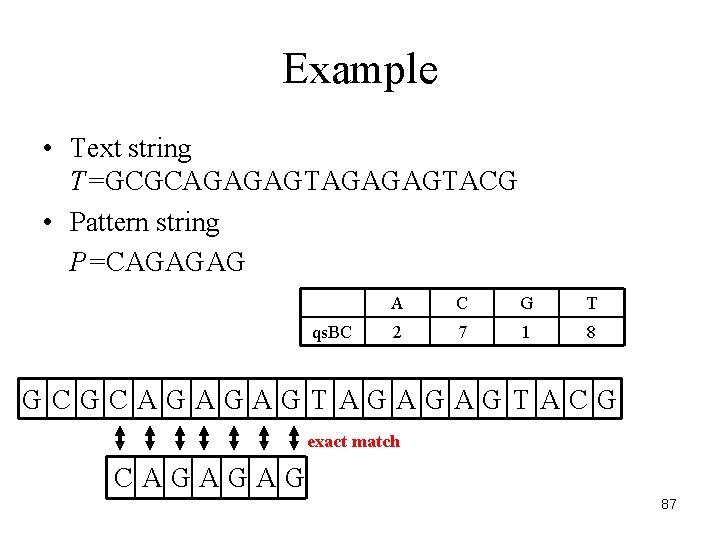
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG exact match CAGAGAG 87

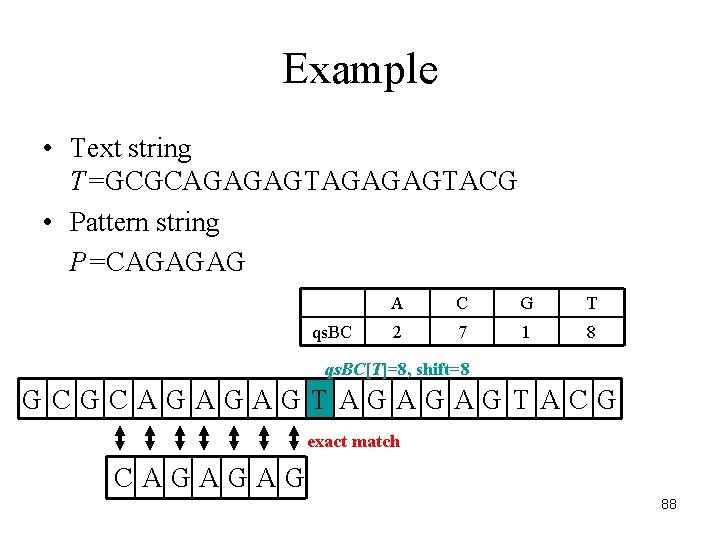
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 qs. BC[T]=8, shift=8 GCGCAGAGAGTACG exact match CAGAGAG 88

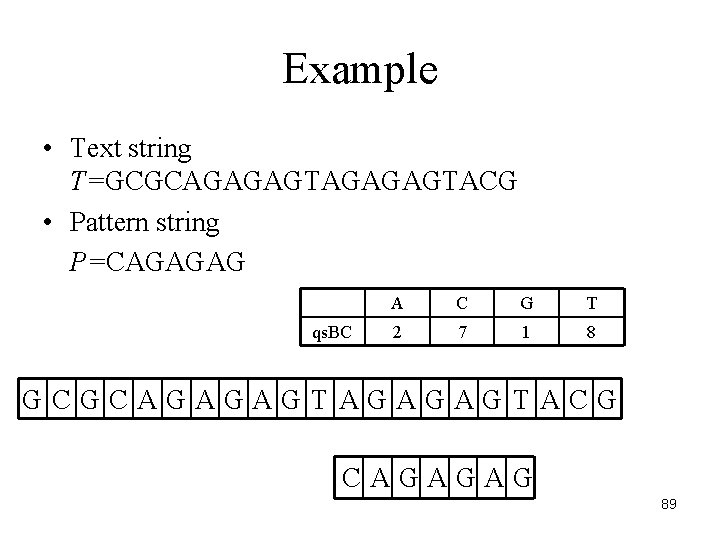
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 89

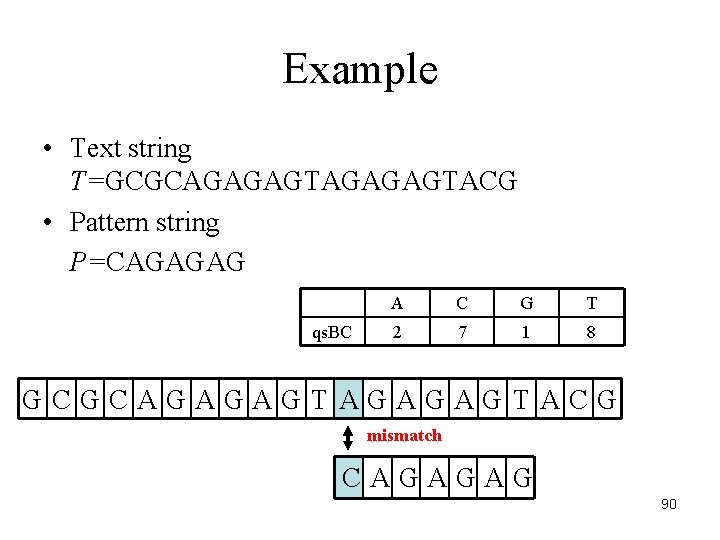
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG mismatch CAGAGAG 90

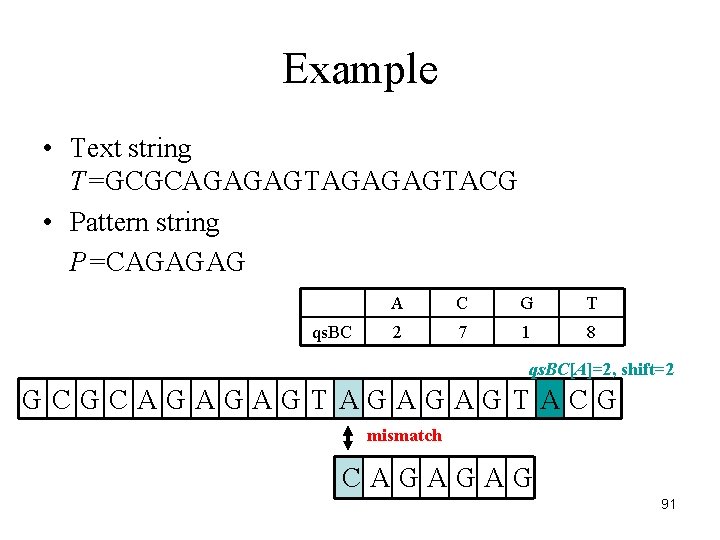
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 qs. BC[A]=2, shift=2 GCGCAGAGAGTACG mismatch CAGAGAG 91

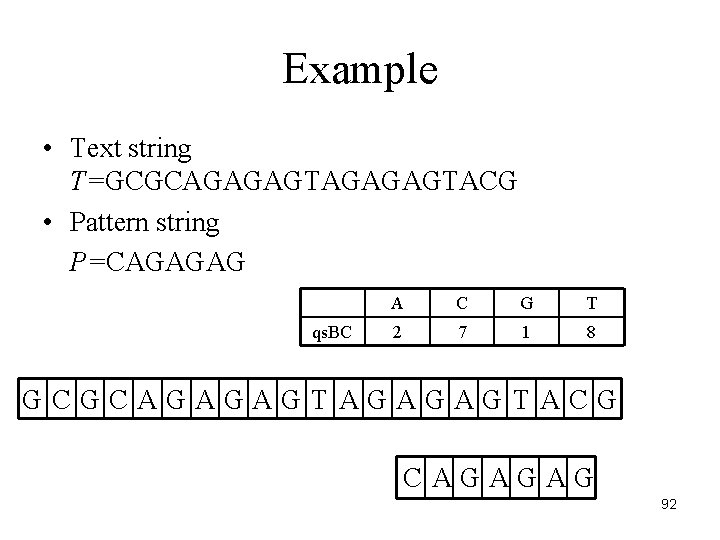
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 92

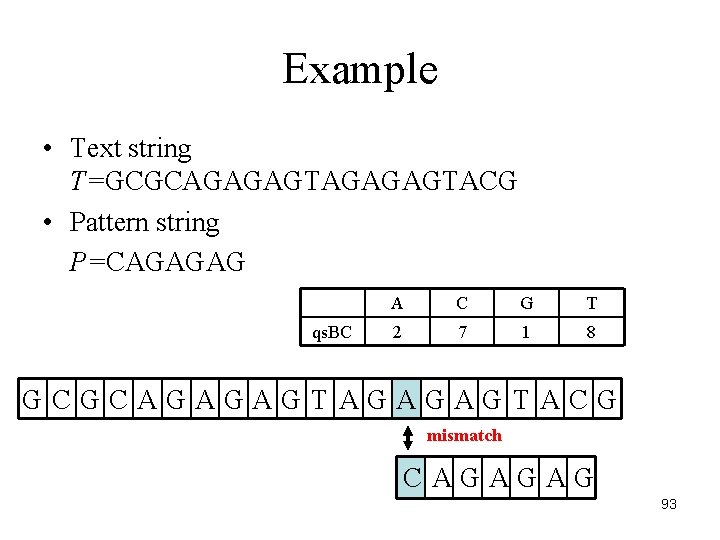
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG mismatch CAGAGAG 93

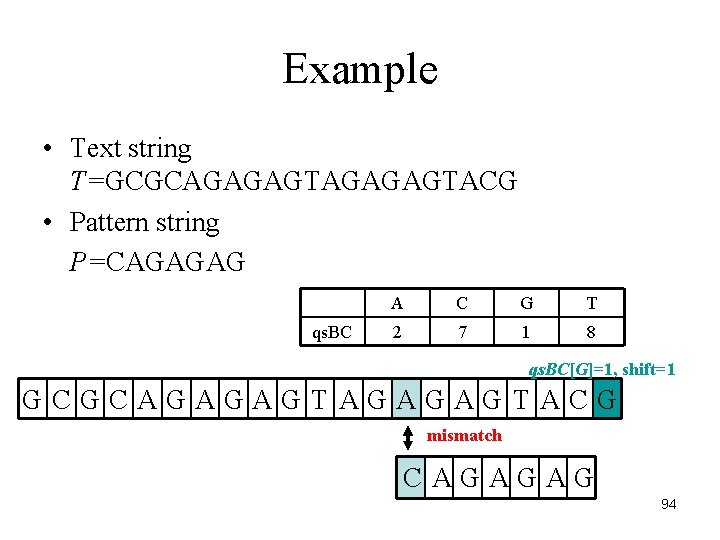
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 qs. BC[G]=1, shift=1 GCGCAGAGAGTACG mismatch CAGAGAG 94

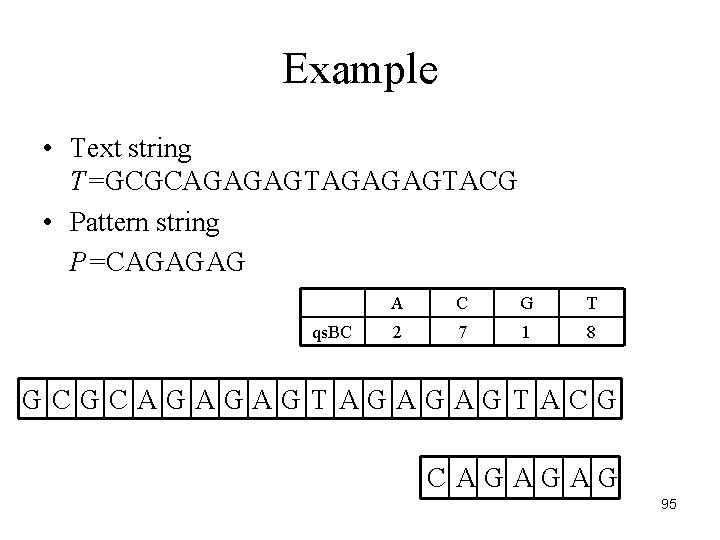
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 95

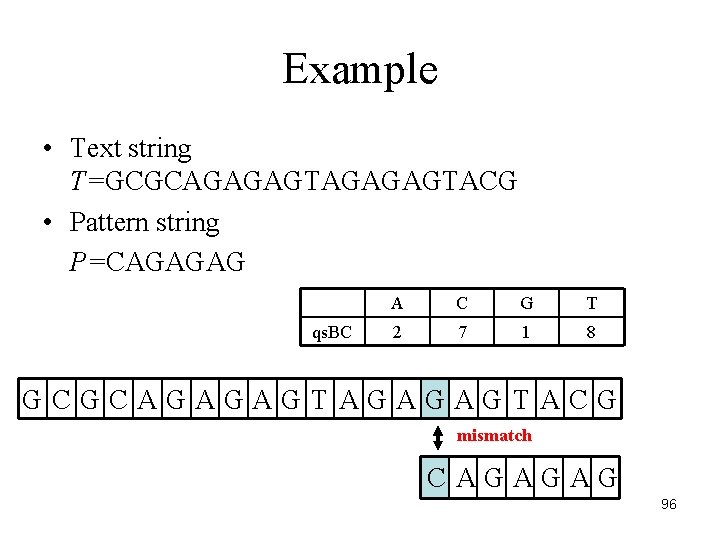
Example • Text string T=GCGCAGAGAGTACG • Pattern string P=CAGAGAG qs. BC A C G T 2 7 1 8 GCGCAGAGAGTACG mismatch CAGAGAG 96

Time complexity • preprocessing phase in O(m+ σ) time and O(σ) space complexity, σ is the number of alphabets in pattern. • searching phase in O(mn) time complexity. 97

Smith Algorithm Experiments with a very fast substring search algorithm, SMITH P. D. , Software Practice & Experience 21(10), 1991, pp. 1065 -1074. 98

Introduction • takes the maximum of the Horspool shift function and the Quick Search shift function. • uses Rule 2 -2: 1 -Suffix Rule 99

Smith Algorithm • This algorithm is almost the same as Quick Search Algorithm except the last character of the window is also considered. If this will induce a better movement than the Quick Search Algorithm. This is used; otherwise the Quick Search is used. 100

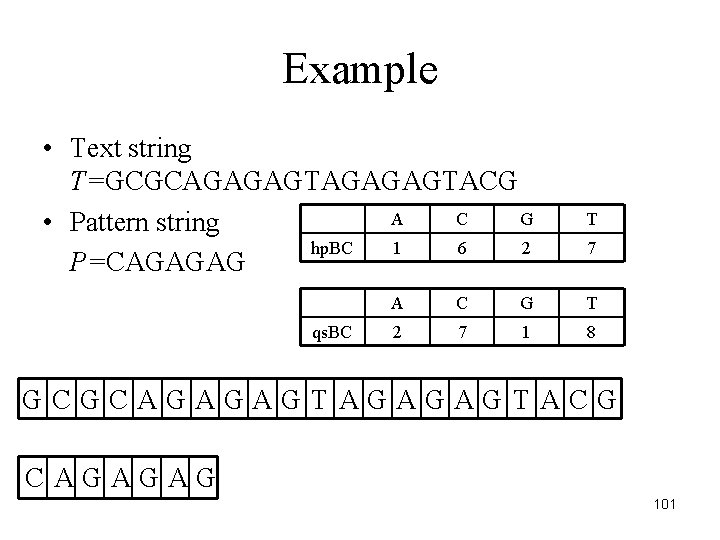
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 101

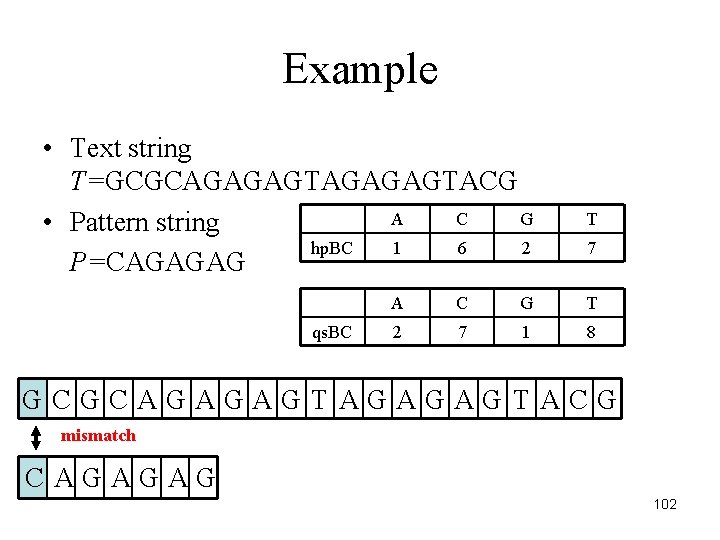
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 GCGCAGAGAGTACG mismatch CAGAGAG 102

Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 hp. BC[A]=1, qs. BC[G]=1, shift=1 GCGCAGAGAGTACG mismatch CAGAGAG 103

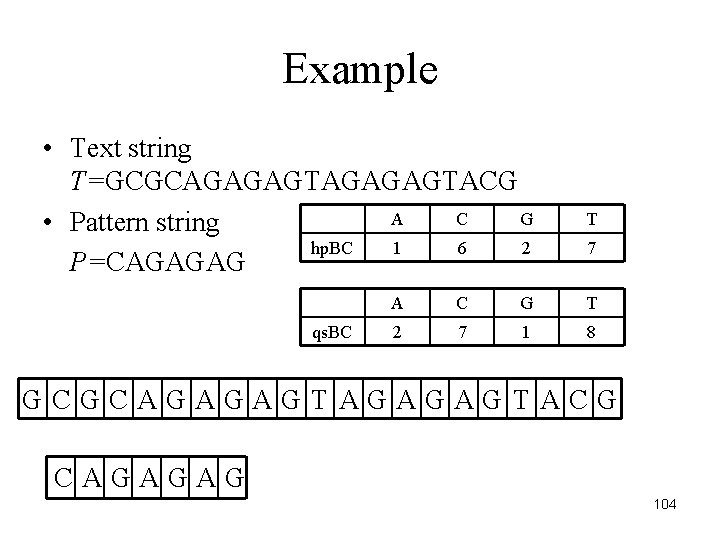
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 104

Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 GCGCAGAGAGTACG mismatch CAGAGAG 105

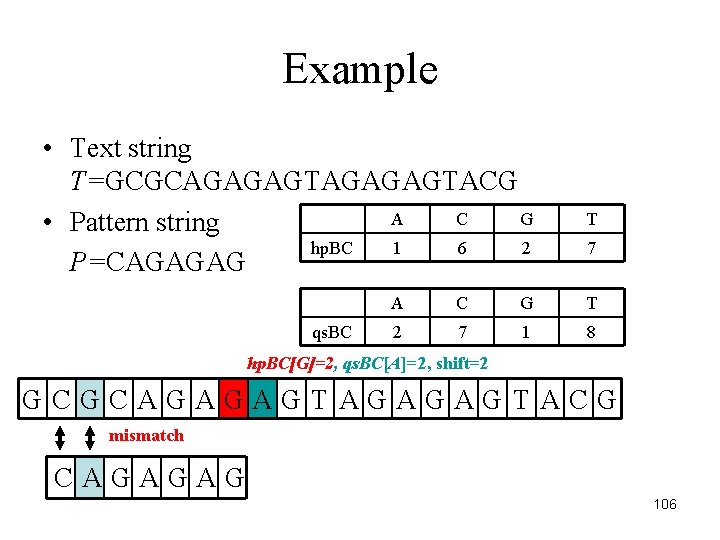
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 hp. BC[G]=2, qs. BC[A]=2, shift=2 GCGCAGAGAGTACG mismatch CAGAGAG 106

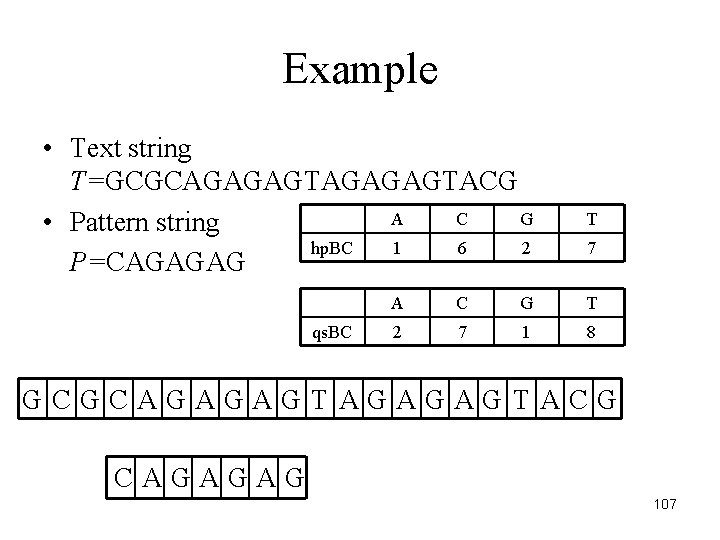
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 107

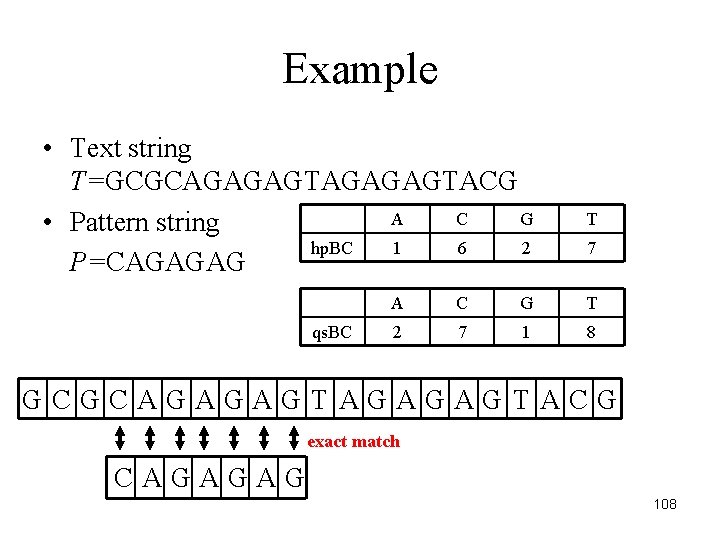
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 GCGCAGAGAGTACG exact match CAGAGAG 108

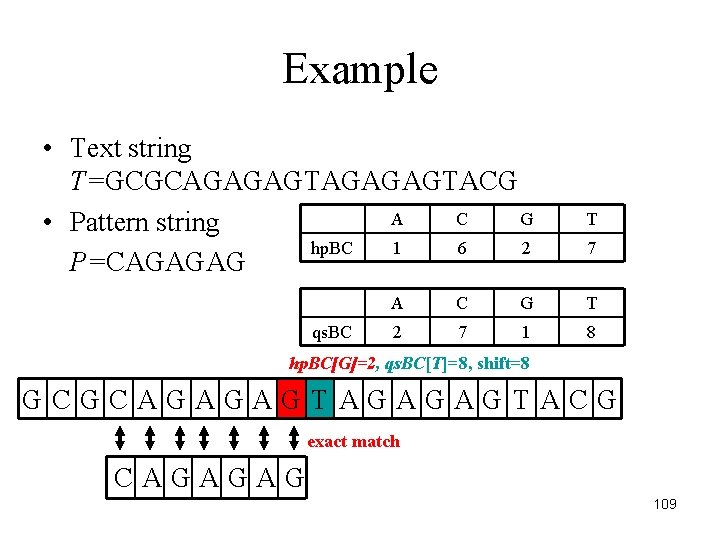
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 hp. BC[G]=2, qs. BC[T]=8, shift=8 GCGCAGAGAGTACG exact match CAGAGAG 109

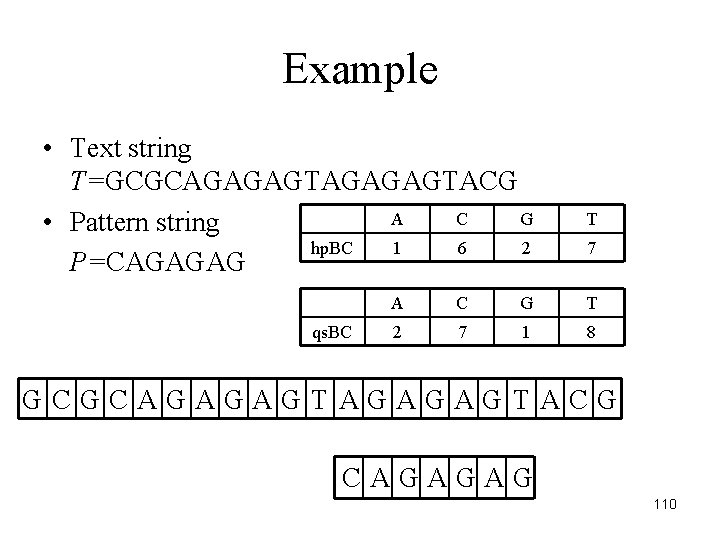
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 110

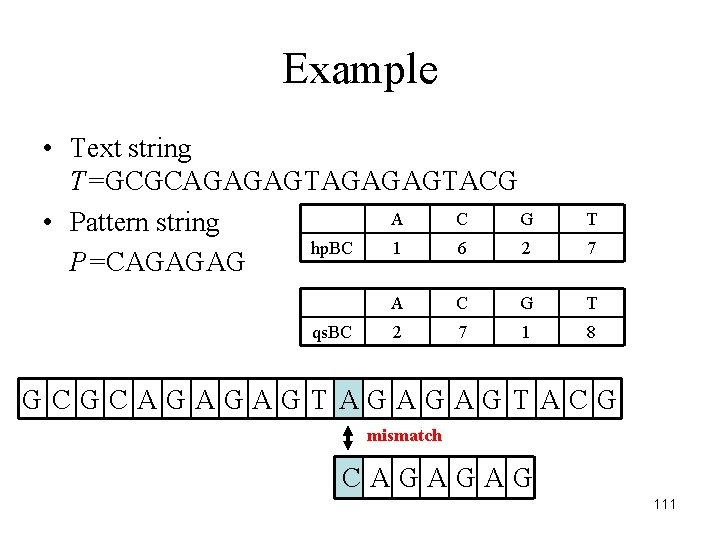
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 GCGCAGAGAGTACG mismatch CAGAGAG 111

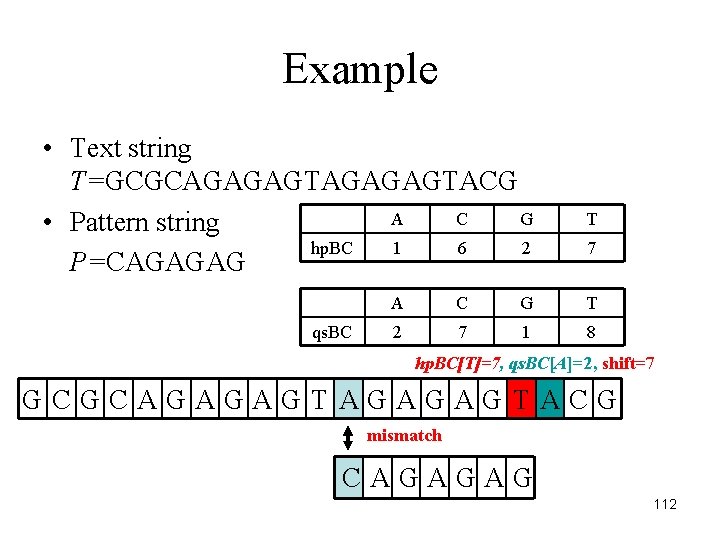
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 hp. BC[T]=7, qs. BC[A]=2, shift=7 GCGCAGAGAGTACG mismatch CAGAGAG 112

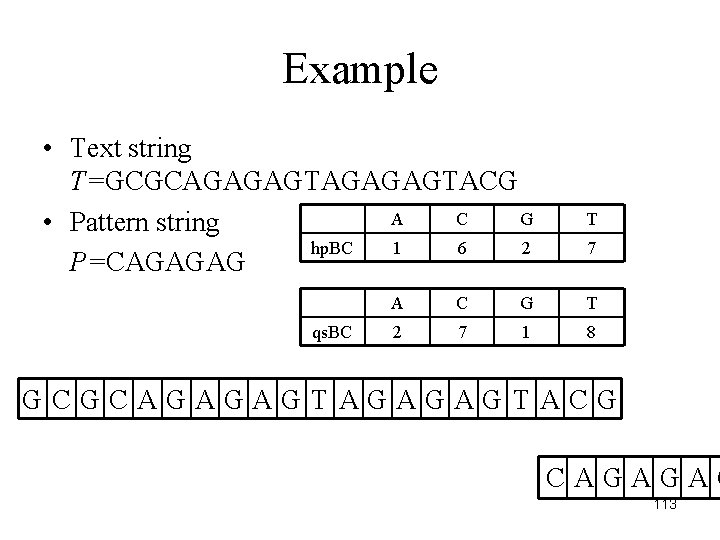
Example • Text string T=GCGCAGAGAGTACG A C G • Pattern string hp. BC 1 6 2 P=CAGAGAG qs. BC T 7 A C G T 2 7 1 8 GCGCAGAGAGTACG CAGAGAG 113

Time complexity • preprocessing phase in O(m+ σ) time and O(σ) space complexity, σ is the number of alphabets in pattern. • searching phase in O(mn) time complexity. 114

Zhu-Takaoka Algorithm On improving the average case of the Boyer. Moore string matching algorithm, R. F. ZHU and T. TAKAOKA, Journal of Information Processing 10(3), 1987, pp. 173 -177 115

• The Zhu-Takaoka Algorithm is a variant of the Boyer and Moore Algorithm. The algorithm only improve the bad character of the Boyer and Moore Algorithm. • Zhu and Takaoka modified the BM Algorithm. They replaced the bad character rule by a 2 -substring rule. The good suffix rules are still used. 116

Rule 2 -3: The 2 -Substring Rule (A Special Version of Rule 2) • Consider the 2 -substring Tk and Tk+1. We may apply Rule 2 -3 now. Tk Tk+1 u x Pj u x Pi Pi+1 v x u x v x 117

Zhu-Takaoka Preprocessing Table The preprocessing phase of the algorithm consists in computing for each pair of characters (a, b) with a, b the rightmost occurrence of ab in x [ 0. . m -2] 118

Case 1 : Þ If zt. Bc[A, C] = k • Example 0 1 2 3 4 5 6 7 8 9 10 11 12 Text G C A T C G C A G A G T A C G Pattern G C A G A Shift by 5 G A G G C A zt. Bc A C G * A 8 8 2 8 C 5 8 7 8 G 1 6 7 8 * 8 8 7 8 ↑ a ←b G A 13 14 15 16 4 5 6 17 18 19 20 21 22 G i 0 1 2 3 7 x[i ] G C A G A G • zt. Bc[C, A] = 5 ; k ≤ m-2 ; ∵ x[8 -5 -2. . 8 -51] = ab (x[1. . 2] = CA) and “CA” does not occur in x[8 -5 -1. . 8 -2] (x[2. . 6] ). 119 23

Case 2 : => If zt. Bc[A, C] = k • Example 0 Text Pattern 1 2 3 4 5 6 7 8 9 10 11 12 13 14 G A G 3 15 16 17 18 19 20 21 22 G C A T C G G A G T A C G G C A G A Shift by 7 G zt. Bc A C G * A 8 8 2 8 C 5 8 7 8 G 1 6 7 8 * 8 8 7 8 ↑ a G C ←b A G A i 0 1 2 4 5 6 7 x[i ] G C A G A G • zt. Bc[C, G] = 7 ; k = m-1 ; ∵ x[0] = b ( G = G) and “CG” does not occur in x[0. . 8 -2] (x[0. . 6] ). 120 23

Case 3 : => If zt. Bc[A, C] = k • Example 0 1 2 3 4 5 6 7 8 9 10 11 12 Text G C A T C G C A G A G T A C G Pattern G C A G A 13 14 15 16 18 19 20 21 22 G zt. Bc A C G * i 0 1 2 A 8 8 2 8 G C A G A G C 5 8 7 8 x[i ] G 1 6 7 8 * 8 8 7 8 ↑ a 17 ←b 3 4 5 6 7 • zt. Bc[A, C] = 8 ; k = m ; ∵ x[0] ≠b (G≠C) and “AC” does not occur in x[0. . 8 -2] ( x[0. . 6] ). 121 23

preprocessing phase Consider text= ATTGCCTAATA and pattern=CTAAG The alphabet of pattern is {A. C. G. T }; The sign “ * ” denotes a word of text which never appears in pattern. First, we fill in the blanks with the length m of pattern. Example: A C G T * A 5 5 5 C 5 5 5 G 5 5 5 T 5 5 5 * 5 5 5 122

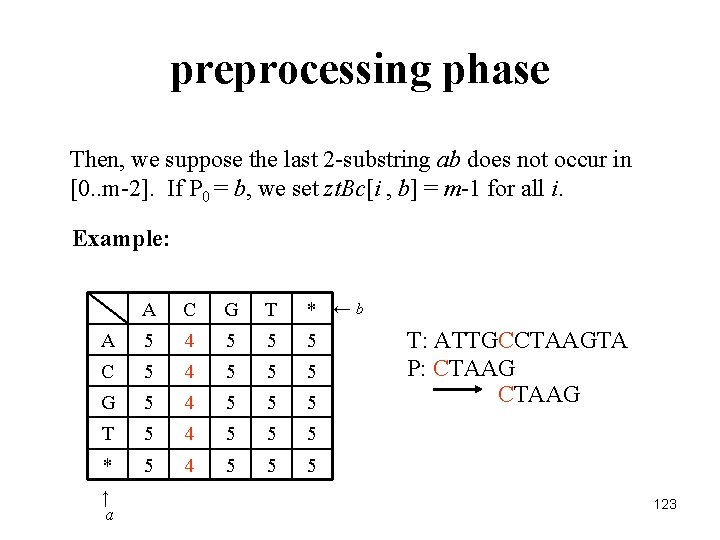
preprocessing phase Then, we suppose the last 2 -substring ab does not occur in [0. . m-2]. If P 0 = b, we set zt. Bc[i , b] = m-1 for all i. Example: A C G T * ←b A 5 4 5 5 5 C 5 4 5 5 5 G 5 4 5 5 5 T 5 4 5 5 5 * 5 4 5 5 5 ↑ a T: ATTGCCTAAGTA P: CTAAG 123

preprocessing phase Finally, we set zt. BC[a, b] = k if k≤ m-2 and P[m-k-2. . m-k-1]=ab and ab does not occur in P[m-k-1. . m-2]. Example: A C G T * ←b A 1 4 5 5 5 C 5 4 5 3 5 G 5 4 5 5 5 T 2 4 5 5 5 * 5 4 5 5 5 ↑ a P: CTAAG 1 2 3 124

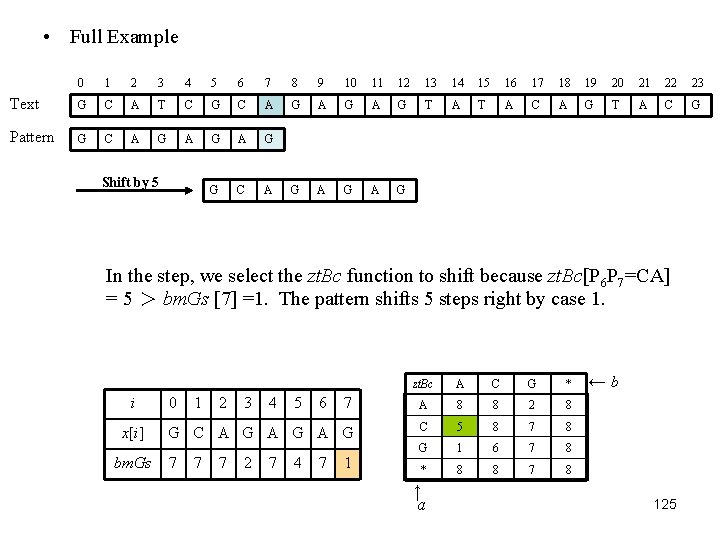
• Full Example 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Text G C A T C G C A G A G T A C G Pattern G C A G A G A G Shift by 5 In the step, we select the zt. Bc function to shift because zt. Bc[P 6 P 7=CA] = 5 ＞ bm. Gs [7] =1. The pattern shifts 5 steps right by case 1. i x[i] bm. Gs zt. Bc A C G * 7 A 8 8 2 8 G C A G A G C 5 8 7 8 G 1 6 7 8 * 8 8 7 8 0 7 1 7 2 7 3 2 4 7 5 4 6 7 1 ↑ a ←b 125

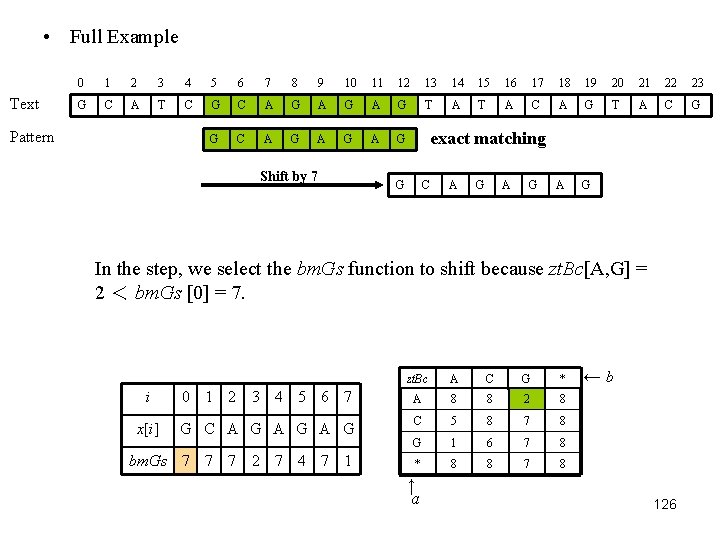
• Full Example Text 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 G C A T C G C A G A G T A C G G C A G A G Pattern Shift by 7 exact matching G C A G In the step, we select the bm. Gs function to shift because zt. Bc[A, G] = 2 ＜ bm. Gs [0] = 7. zt. Bc A C G * i 0 1 2 3 4 5 6 7 A 8 8 2 8 x[i] G C A G A G C 5 8 7 8 G 1 6 7 8 * 8 8 7 8 bm. Gs 7 7 7 2 7 4 7 1 ↑ a ←b 126

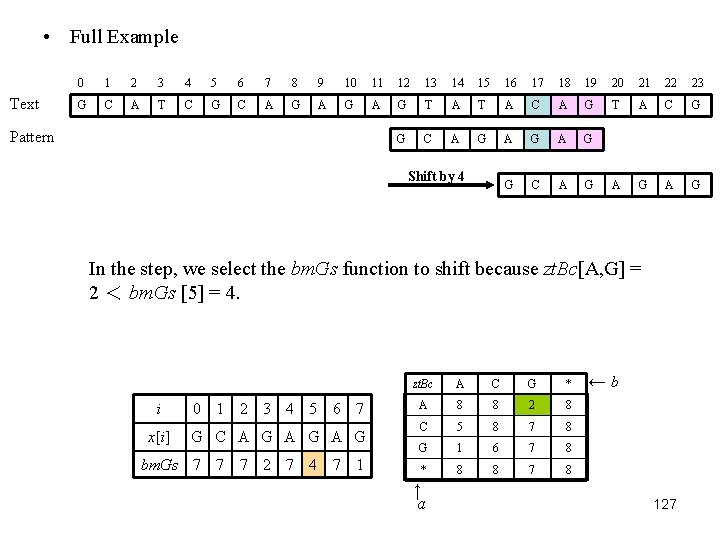
• Full Example Text 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 G C A T C G C A G A G T A C G G C A G A G A G Pattern Shift by 4 In the step, we select the bm. Gs function to shift because zt. Bc[A, G] = 2 ＜ bm. Gs [5] = 4. i 0 1 2 3 4 5 6 7 x[i] G C A G A G bm. Gs 7 7 7 2 7 4 7 1 zt. Bc A C G * A 8 8 2 8 C 5 8 7 8 G 1 6 7 8 * 8 8 7 8 ↑ a ←b 127

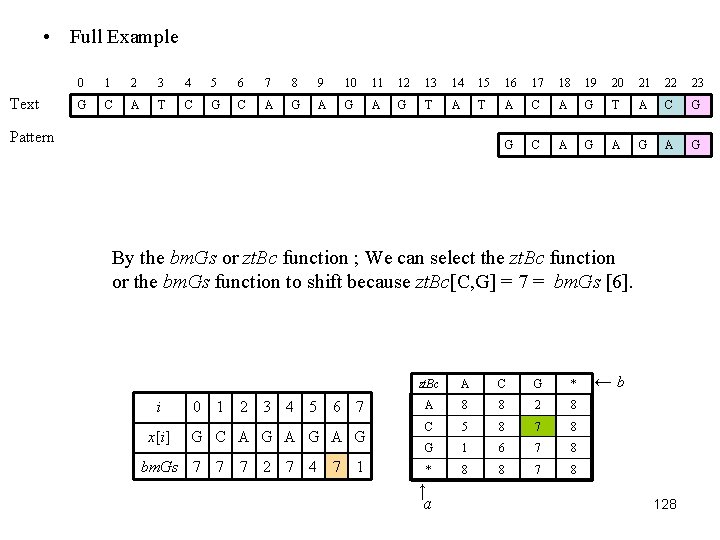
• Full Example Text 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 G C A T C G C A G A G T A C G G C A G A G Pattern By the bm. Gs or zt. Bc function ; We can select the zt. Bc function or the bm. Gs function to shift because zt. Bc[C, G] = 7 = bm. Gs [6]. i 0 1 2 3 4 5 6 7 x[i] G C A G A G bm. Gs 7 7 7 2 7 4 7 1 zt. Bc A C G * A 8 8 2 8 C 5 8 7 8 G 1 6 7 8 * 8 8 7 8 ↑ a ←b 128

Time complexity • preprocessing phase in O(m＋ ) time and space complexity. Ø( = the numbers of alphabet of the text ). • searching phase in O(m × n) time complexity. 129

Reference [KMP 77] Fast pattern matching in strings, D. E. Knuth, J. H. Morris, Jr and V. B. Pratt, SIAM J. Computing, 6, 1977, pp. 323– 350. [BM 77] A fast string search algorithm, R. S. Boyer and J. S. Moore, Comm. ACM, 20, 1977, pp. 762– 772. [S 90] A very fast substring search algorithm, D. M. Sunday, Comm. ACM, 33, 1990, pp. 132– 142. [RR 89] The Rand MH Message Handling system: User’s Manual (UCIVersion), M. T. Rose and J. L. Romine, University of California, Irvine, 1989. [S 82] A comparison of three string matching algorithms, G. De V. Smith, Software—Practice and Experience, 12, 1982, pp. 57– 66. [HS 91] Fast string searching, HUME A. and SUNDAY D. M. , Software - Practice & Experience 21(11), 1991, pp. 1221 -1248. [S 94] String Searching Algorithms , Stephen, G. A. , World Scientific, 1994. [ZT 87] On improving the average case of the Boyer-Moore string matching algorithm, ZHU, R. F. and TAKAOKA, T. , Journal of Information Processing 10(3) , 1987, pp. 173 -177. [R 92] Tuning the Boyer-Moore-Horspool string searching algorithm, RAITA T. , Software - Practice & Experience, 22(10) , 1992, pp. 879 -884. [S 94] On tuning the Boyer-Moore-Horspool string searching algorithms, SMITH, P. D. , Software - Practice & Experience, 24(4) , 1994, pp. 435 -436. [BR 92] Average running time of the Boyer-Moore-Horspool algorithm, BAEZA-YATES, R. A. , RÉGNIER, M. , Theoretical Computer Science 92(1) , 1992, pp. 19 -31. [H 80] Practical fast searching in strings, HORSPOOL R. N. , Software - Practice & Experience, 10(6) , 1980, pp. 501 -506. [L 95] Experimental results on string matching algorithms, LECROQ, T. , Software - Practice & Experience 25(7) 130 , 1995, pp. 727 -765.

Thanks for your listening 131