Tun 9 10 11 12 CC THUT TON

Tuần 9, 10, 11, 12: CÁC THUẬT TOÁN VỀ ĐỒ THỊ

CÁC KHÁI NiỆM VỀ ĐỒ THỊ

Các khái niệm về đồ thị v Khái niệm: - Đồ thị là tập các đỉnh và các cạnh. G = (V, E) - Cạnh là đường kết nối giữa 2 đỉnh - Có 2 loại đồ thị: - Đồ thị vô hướng (undirected graphs) – Graph - Đồ thị có hướng (directed graphs) - Digraph v. Ví dụ đồ thị vô hướng: G = ({1, 2, 3, 4, 5}, {{1, 2}, {1, 3}, {2, 4}, {3, 5}, {4, 5}})

Các khái niệm về đồ thị v. Thuật ngữ: - Một đồ thị đầy đủ: (Complete Graph)Là 1 đỉnh sẽ đi đến tất cả các đỉnh khác. Đồ thị có N đỉnh Có (N 2 -N)/2 cạnh - Một đồ thị có hướng đầy đủ (Complete Digraph) với N đỉnh (N 2 -N) cạnh - Gs=(Vs, Es) là đồ thị con (Subgraph)của G=(V, E) nếu Vs là tập con của V và Es là tập con của E

Các khái niệm về đồ thị v. Thuật ngữ: - Đường đi giữa 2 đỉnh A, B (Path): bắt đầu từ đỉnh A, qua một số đỉnh, và kết thúc là đỉnh B - Đồ thị có trọng số (weighted graph) là mỗi cạnh của đồ thị có giá trị - Đường đi của đồ thị có trọng số là tổng giá trị của mỗi cạnh - Đường đi ngắn nhất giữa 2 đỉnh: là đường đi có trọng số nhỏ nhất

Các khái niệm về đồ thị v. Thuật ngữ: - Một đồ thị gọi là liên thông (connected) nếu như có ít nhất 1 đường đi nối tất cả các đỉnh - Chu trình (cycle) là đường đi bắt đầu từ 1 đỉnh và kết thúc tại đỉnh đó. - Một đồ thị không có chu trình được gọi là cây (tree)

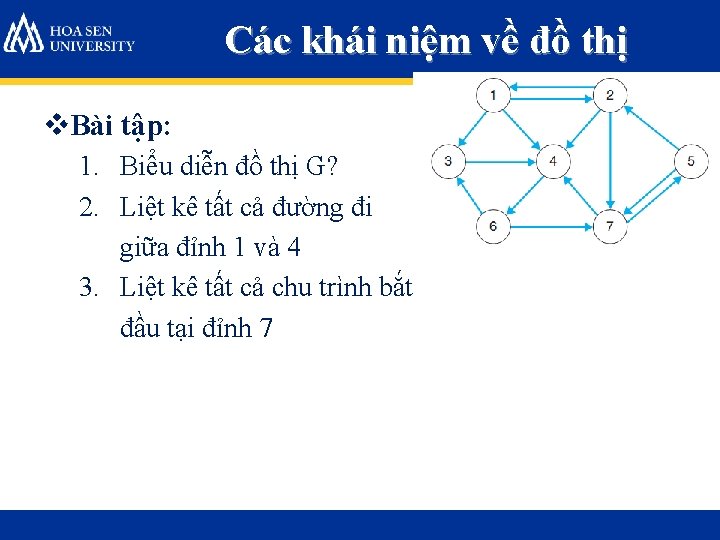
Các khái niệm về đồ thị v. Bài tập: 1. Biểu diễn đồ thị G? 2. Liệt kê tất cả đường đi giữa đỉnh 1 và 4 3. Liệt kê tất cả chu trình bắt đầu tại đỉnh 7

CẤU TRÚC DỮ LiỆU CHO ĐỒ THỊ

Cấu trúc dữ liệu cho đồ thị v Biểu diễn đồ thị: Có 2 cách - Ma trận kế cận (adjacency matrix): có khả năng cập nhật thông tin của cạnh nhanh chóng, tuy nhiên không đầy đủ - Tập danh sách kế cận (adjacency list): Biểu diễn đầy đủ thông tin về cạnh, tuy nhiên cần nhiều thời gian hơn để cập nhật thông tin - Đối với đồ thị có nhiều đỉnh, nhưng số cạnh không nhiều Tập danh sách kề là tối ưu để biểu diễn đồ thị

Cấu trúc dữ liệu cho đồ thị v Ma trận kề: - Biểu diễn đồ thị G=(V, E) bằng ma trận kề |V| với N hàng, N cột với các giá trị 0, 1 |V|= 0 Nếu không tồn tại cạnh giữa vivj 1 Nếu tồn tại cạnh giữa vivj - Đồ thị có trọng số: Giá trị của ma trận kề gồm trọng số của các cạnh

Cấu trúc dữ liệu cho đồ thị v. Ví dụ: Biểu diễn ma trận kề cho các đồ thị sau 1 2 3 4 5 1 0 1 1 0 0 2 1 0 1 1 0 2 1 0 0 3 1 1 0 0 1 3 0 1 0 0 0 4 0 1 0 0 1 4 0 0 1 5 0 0 1 1 0 5 0 1 0

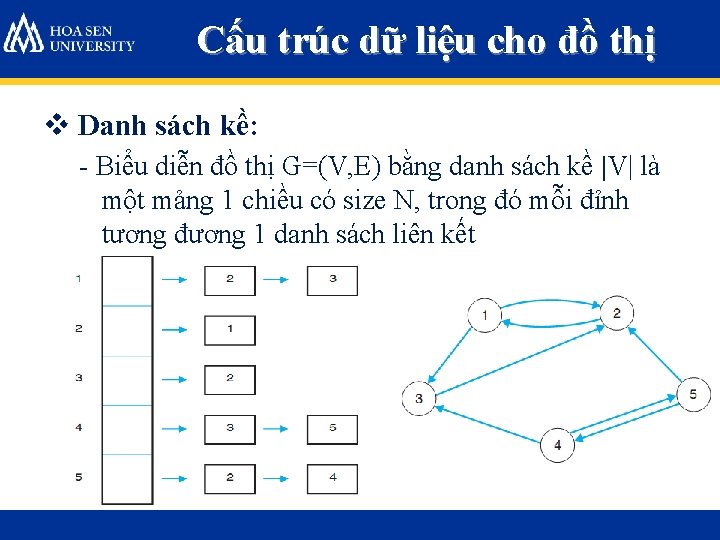
Cấu trúc dữ liệu cho đồ thị v Danh sách kề: - Biểu diễn đồ thị G=(V, E) bằng danh sách kề |V| là một mảng 1 chiều có size N, trong đó mỗi đỉnh tương đương 1 danh sách liên kết

Cấu trúc dữ liệu cho đồ thị v. Bài tập: 1. Biểu diễn danh sách kề cho đồ thị 1 2. Biểu diễn ma trận kề cho đồ thị sau

Cấu trúc dữ liệu cho đồ thị v. Cài đặt ma trận kề: #define max 100 struct Graph { int n; int a[max]; }; vĐịnh dạng dữ liệu: Dữ liệu vào ma trận kề được lưu ở file: 1. Dòng đầu tiên: số đỉnh của đồ thị 2. Mỗi dòng chứa n số nguyên ứng với giá trị trong ma trận kề

Cấu trúc dữ liệu cho đồ thị vĐọc ma trận kề từ file: void Matranke (Graph &g) { char file[128]; printf(“Tap tin nguon (Dothi. txt)”); gets(file); if (strcmp(file, ””)==0) strcpy(file, ”Dothi. txt”); FILE *f; f = fopen(file, ”rt”);

Cấu trúc dữ liệu cho đồ thị if ( f==NULL) { printf(“Khong mo duoc file”); exit(0); } fscanf(f, ”%d”, &g. n); for (int i=0; i<g. n; i++) for (int j =0; j<g. n; j++) fscanf (f, ”%d”, &g. a[i][j]); fclose(f); }

THUẬT TOÁN DUYỆT ĐỒ THỊ

Tổng quan v Duyệt hay tìm kiếm trên đồ thị: ghé qua mỗi đỉnh trong đồ thị một cách có hệ thống - Duyệt đồ thị không phụ thuộc vào hướng của cạnh v Có 2 cách duyệt đồ thị: - Duyệt theo chiều sâu – DFS ( Depth-first-search) - Duyệt theo chiều rộng – BFS (Breadth-first-search)

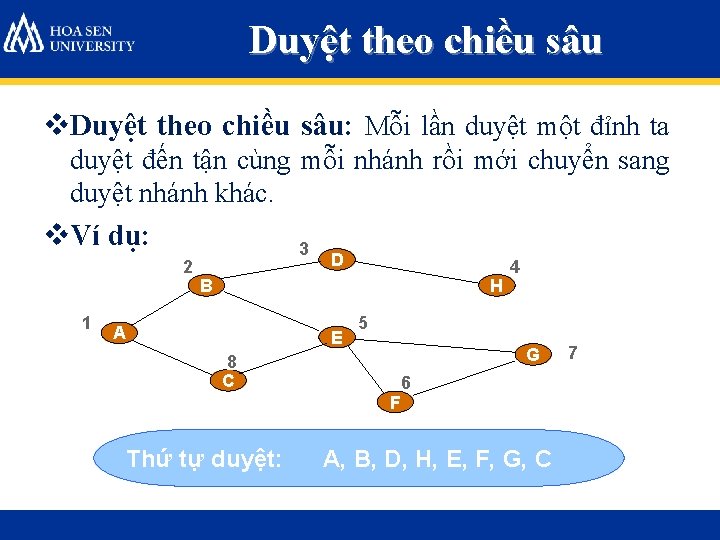
Duyệt theo chiều sâu v. Duyệt theo chiều sâu: Mỗi lần duyệt một đỉnh ta duyệt đến tận cùng mỗi nhánh rồi mới chuyển sang duyệt nhánh khác. v. Ví dụ: 2 1 3 D B H A E 5 G 8 C F Thứ tự duyệt: 4 6 A, B, D, H, E, F, G, C 7

Duyệt theo chiều sâu v. Thuật toán: - Chọn 1 đỉnh làm điểm bắt đầu - Bắt đầu duyệt từ đầu cho đến tận cùng của nhánh - Sau đó sẽ quay lại đoạn đường đã duyệt, và duyệt tiếp những đỉnh kề chưa được duyệt - Quá trình sẽ kết thúc khi quay lại đỉnh bắt đầu và tất cả các đỉnh đã được duyệt. - Trong quá trình duyệt, nếu 1 đỉnh sẽ rẽ qua nhiều hơn 1 đỉnh, thì ta chọn đỉnh có số hoặc chữ cái nhỏ hơn

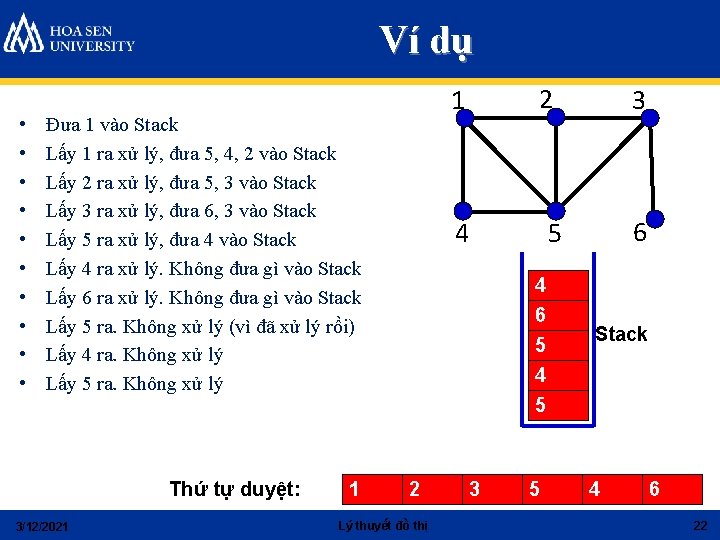
Ví dụ • • • Đưa 1 vào Stack Lấy 1 ra xử lý, đưa 5, 4, 2 vào Stack Lấy 2 ra xử lý, đưa 5, 3 vào Stack Lấy 3 ra xử lý, đưa 6, 3 vào Stack Lấy 5 ra xử lý, đưa 4 vào Stack Lấy 4 ra xử lý. Không đưa gì vào Stack Lấy 6 ra xử lý. Không đưa gì vào Stack Lấy 5 ra. Không xử lý (vì đã xử lý rồi) Lấy 4 ra. Không xử lý Lấy 5 ra. Không xử lý Thứ tự duyệt: 3/12/2021 1 2 1 4 Lý thuyết đồ thị 3 6 5 4 5 3 6 5 2 4 1 5 2 3 5 Stack 4 6 22

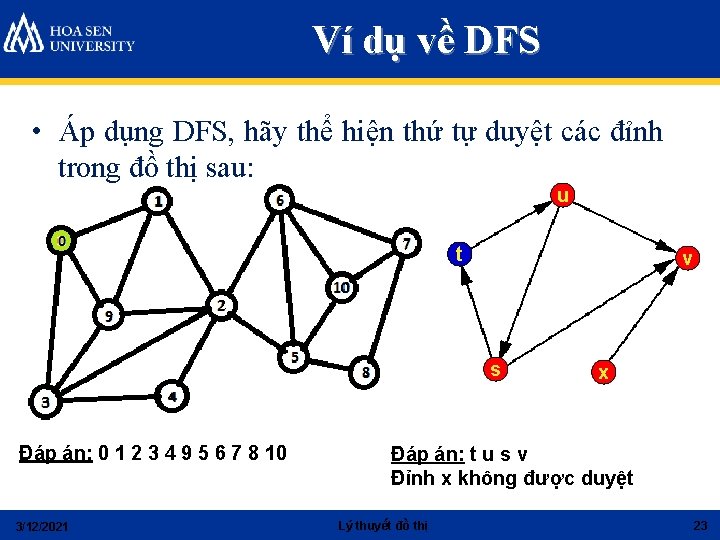
Ví dụ về DFS • Áp dụng DFS, hãy thể hiện thứ tự duyệt các đỉnh trong đồ thị sau: u t v s Đáp án: 0 1 2 3 4 9 5 6 7 8 10 3/12/2021 x Đáp án: t u s v Đỉnh x không được duyệt Lý thuyết đồ thị 23

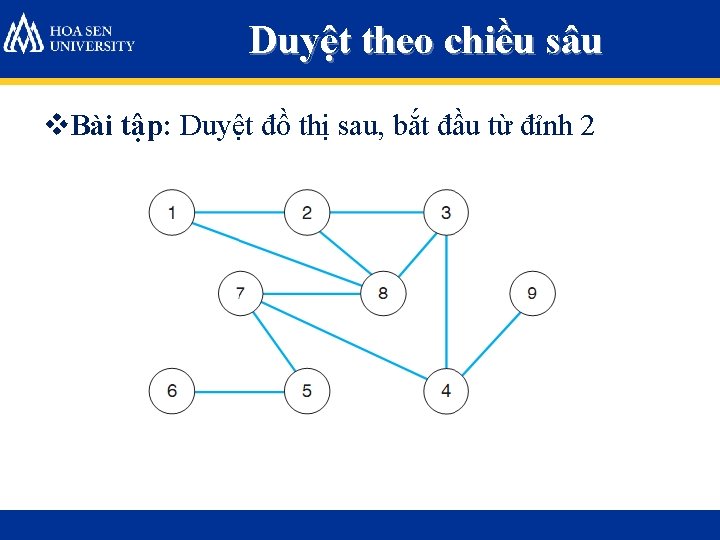
Duyệt theo chiều sâu v. Bài tập: Duyệt đồ thị sau, bắt đầu từ đỉnh 2

Duyệt theo chiều sâu v. Giải thuật: Sử dụng đệ qui void DFS (bool mark[][max], int trace[], int nodes, int u) { for (int v=0; v<nodes; v++) { if ((mark 1[u][v] ==true) && (trace[v] ==0) { trace[v]=u; DFS(mark, trace, nodes, v); } } }

Duyệt theo chiều sâu v. Nhận xét: - Duyệt theo chiều sâu của đồ thị biểu diễn bằng danh sách kề có độ phức tạp O(n+m) // n- Số đỉnh, m- Số cạnh - Duyệt theo chiều sâu của đồ thị biểu diễn bằng ma trận kề có độ phức tạp O(n 2) - Duyệt theo chiều sâu thì đỉnh duyệt càng sớm thì càng kết thúc muộn. - Dùng một ngăn xếp lưu trữ các đỉnh đang duyệt để cải tiến thuật toán

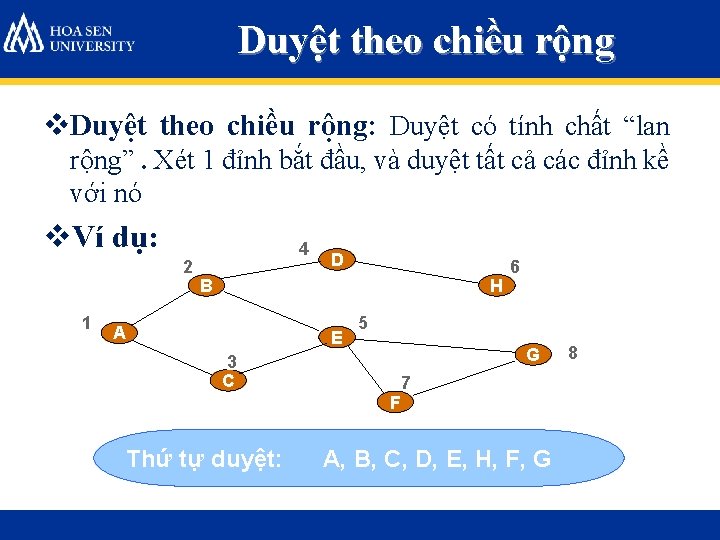
Duyệt theo chiều rộng v. Duyệt theo chiều rộng: Duyệt có tính chất “lan rộng”. Xét 1 đỉnh bắt đầu, và duyệt tất cả các đỉnh kề với nó v. Ví dụ: 2 1 4 D B H A E 5 G 3 C F Thứ tự duyệt: 6 7 A, B, C, D, E, H, F, G 8

Duyệt theo chiều rộng v. Thuật toán: - Chọn 1 đỉnh trong đồ thị để bắt đầu - Từ đỉnh đầu tiên, đi hết tất cả các đỉnh liên thông với nó - Tiếp tục xét với đỉnh thứ 2… - Quá trình kết thúc khi duyệt xong tất cả các đỉnh

Ví dụ 2 1 • • • Đưa 1 vào Queue Lấy 1 ra xử lý, đưa 5, 4, 2 vào Queue Lấy 2 ra xử lý, đưa 5, 3 vào Queue Lấy 4 ra xử lý, đưa 5 vào Queue Lấy 5 ra xử lý, đưa 3 vào Queue Lấy 3 ra xử lý. Đưa 6 vào Queue Lấy 5 ra. Không xử lý (vì đã xử lý rồi) Lấy 5 ra. Không xử lý Lấy 3 ra. Không xử lý Lấy 6 ra xử lý. Không đưa gì vào Queue Thứ tự duyệt: 3/12/2021 1 4 6 3 5 5 3 5 4 1 2 2 Lý thuyết đồ thị 4 5 3 6 5 Queue 3 6 29

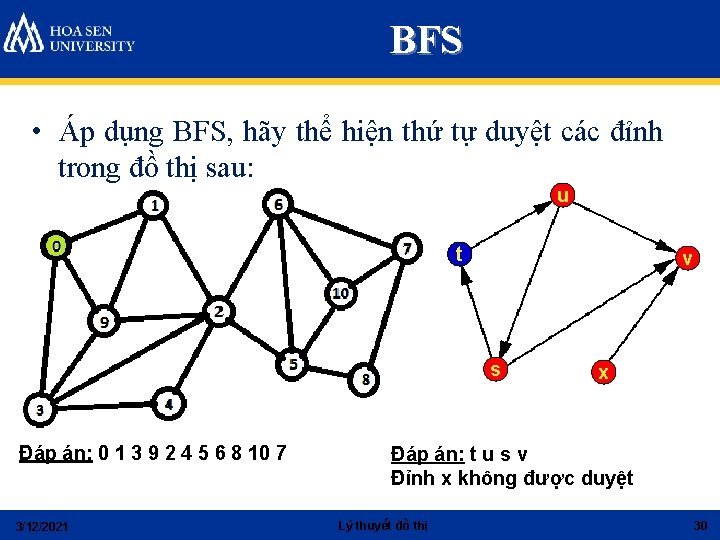
BFS • Áp dụng BFS, hãy thể hiện thứ tự duyệt các đỉnh trong đồ thị sau: u t v s Đáp án: 0 1 3 9 2 4 5 6 8 10 7 3/12/2021 x Đáp án: t u s v Đỉnh x không được duyệt Lý thuyết đồ thị 30

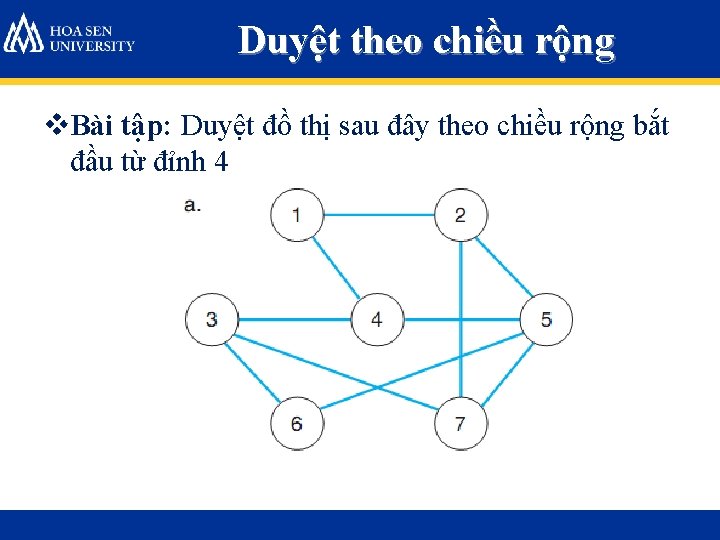
Duyệt theo chiều rộng v. Bài tập: Duyệt đồ thị sau đây theo chiều rộng bắt đầu từ đỉnh 4

Duyệt theo chiều rộng v. Giải thuật: void BFS (queue Q, int trace[], bool mark[][max], int start, int nodes) { int u; Q. push(start); trace[start]=-1; do{ u=Q. front(); Q. pop(); for ( int v=0; v<nodes; v++) { if ((mark[u][v]==true) && trace[v]=0; { Q. push(v); trace[v]=u; } } }while (!Q. empty()); }

Duyệt theo chiều rộng v. Nhận xét: - Duyệt theo chiều sâu và duyệt theo chiều rộng chỉ khác nhau ở chỗ giải thuật DFS sử dụng Stack, và giải thuật BFS sử dụng Queue. Do đó độ phức tạp của DFS và BFS là như nhau - Duyệt theo chiều rộng thì đỉnh được xét càng sớm thì sẽ sớm duyệt xong.

DFS - Chỉ quan tâm đến hướng đi đã chọn. - Có thể đi vào các ngõ, nhánh cụt (không thể đi tiếp được nữa) quay lui BFS - Quan tâm đến tất cả hướng đi tốn bộ nhớ để lưu trữ - Không cần quay lui

C Y BAO TRÙM TỐI THIỂU Minimum spanning tree

Minimum spanning tree v. Khái niệm: - Cây bao trùm tối thiểu MST (minimum spanning tree) của một đồ thị có trọng số là một tập hợp các cạnh kết nối tất cả các đỉnh sao cho tổng trọng số của các cạnh là nhỏ nhất - MST không nhất thiết là duy nhất trong một đồ thị

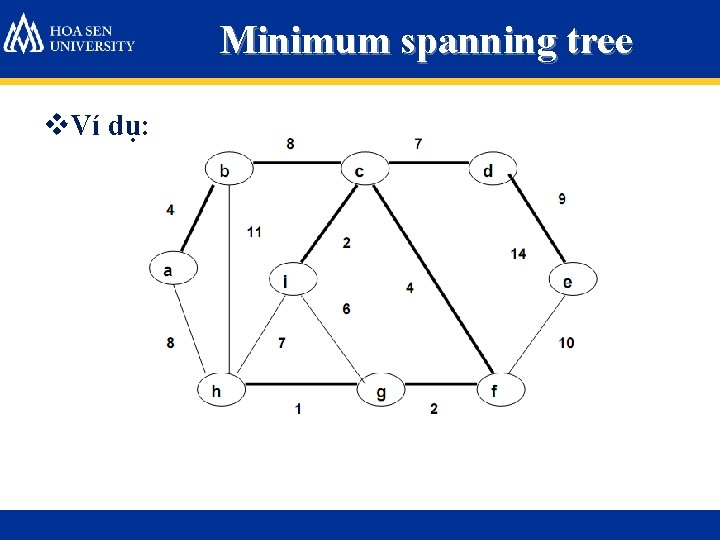
Minimum spanning tree v. Ví dụ:

Thuật toán Dijkstra-Prim v. Giới thiệu: - Thuật toán do Edsger Dijkstra và R. C. Prim tìm ra vào năm 1950 một cách độc lập - Giải thuật Prim dùng để giải bài toán cây bao trùm tối thiểu. - Giải thuật này sử dụng chiến lược để giải một bài toán tối ưu hóa: giải thuật tham lam (greedy): Tại mỗi bước của giải thuật, ta phải chọn một trong một số khả năng lựa chọn. Chiến lược tham lam đề xuất việc lựa chọn khả năng tốt nhất tại lúc đó.

Thuật toán Dijkstra-Prim v. Giới thiệu: - Một chiến lược như vậy thường không đảm bảo đem lại lời giải tối ưu toàn cục cho các bài toán. - Tuy nhiên, đối với bài toán MST, giải thuật tham lam có thể đem lại MST với tổng trọng số tối thiểu

Thuật toán Dijkstra-Prim v. Giải thuật: - Chọn một đỉnh A bắt đầu trong đồ thị - Xây dựng một tập hợp Q bao gồm các đỉnh được nối từ đỉnh A - Chọn đỉnh tiếp theo trong tập Q sao có cạnh từ đỉnh A đến là nhỏ nhất - Tiếp tục thêm vào Q những đỉnh bắt đầu tử đỉnh thứ 2 - Vòng lặp tiếp tục cho đến khi tất cả các đỉnh được duyệt qua

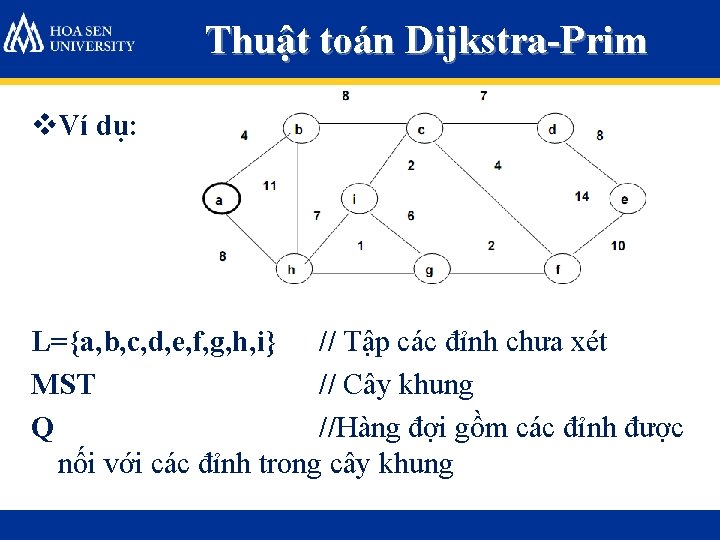
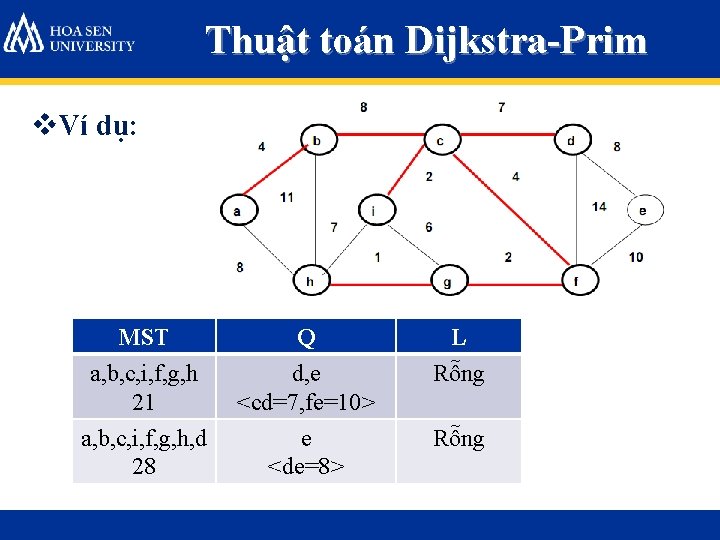
Thuật toán Dijkstra-Prim v. Ví dụ: L={a, b, c, d, e, f, g, h, i} // Tập các đỉnh chưa xét MST // Cây khung Q //Hàng đợi gồm các đỉnh được nối với các đỉnh trong cây khung

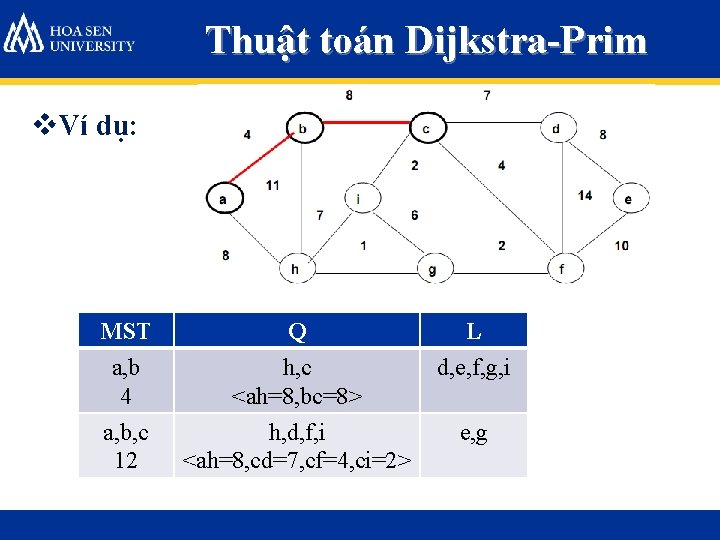
Thuật toán Dijkstra-Prim v. Ví dụ: MST Q L Rỗng a, b, c, d, e, f, g, h, i a b, h <ab=4, ah=8> c, d, e, f, g, i a, b 4 h, c <ah=8, bc=8> d, e, f, g, i

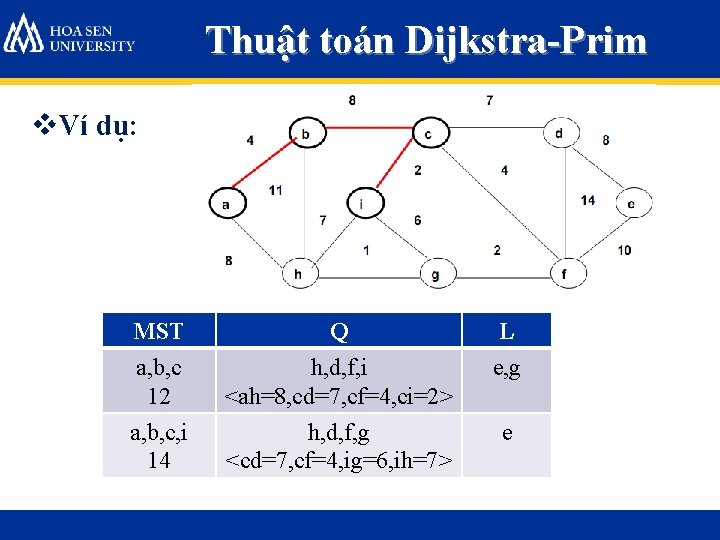
Thuật toán Dijkstra-Prim v. Ví dụ: MST Q L a, b 4 h, c <ah=8, bc=8> d, e, f, g, i a, b, c 12 h, d, f, i <ah=8, cd=7, cf=4, ci=2> e, g

Thuật toán Dijkstra-Prim v. Ví dụ: MST Q L a, b, c 12 h, d, f, i <ah=8, cd=7, cf=4, ci=2> e, g a, b, c, i 14 h, d, f, g <cd=7, cf=4, ig=6, ih=7> e

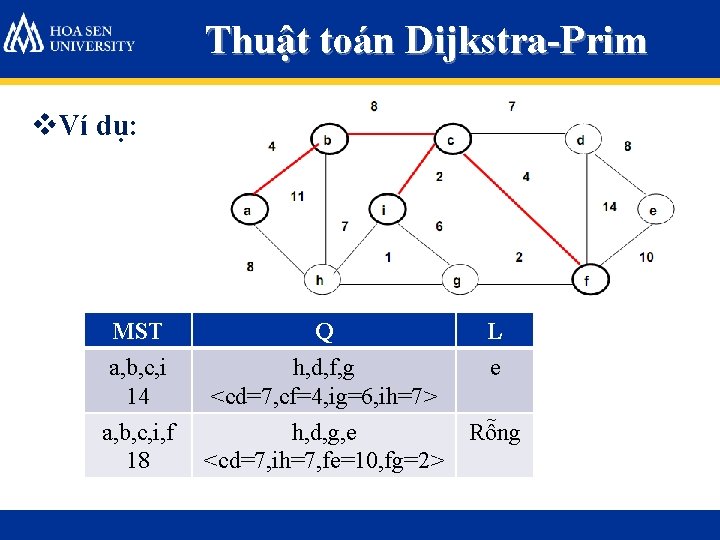
Thuật toán Dijkstra-Prim v. Ví dụ: MST Q L a, b, c, i 14 h, d, f, g <cd=7, cf=4, ig=6, ih=7> e a, b, c, i, f 18 h, d, g, e <cd=7, ih=7, fe=10, fg=2> Rỗng

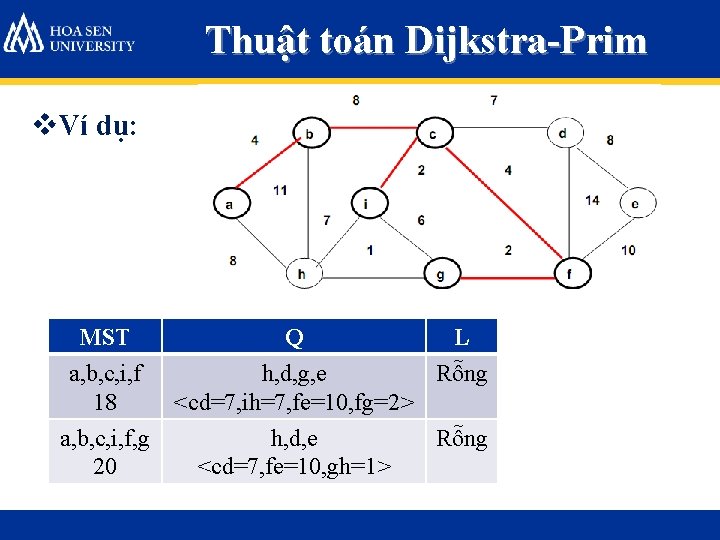
Thuật toán Dijkstra-Prim v. Ví dụ: MST a, b, c, i, f 18 a, b, c, i, f, g 20 Q L h, d, g, e Rỗng <cd=7, ih=7, fe=10, fg=2> h, d, e <cd=7, fe=10, gh=1> Rỗng

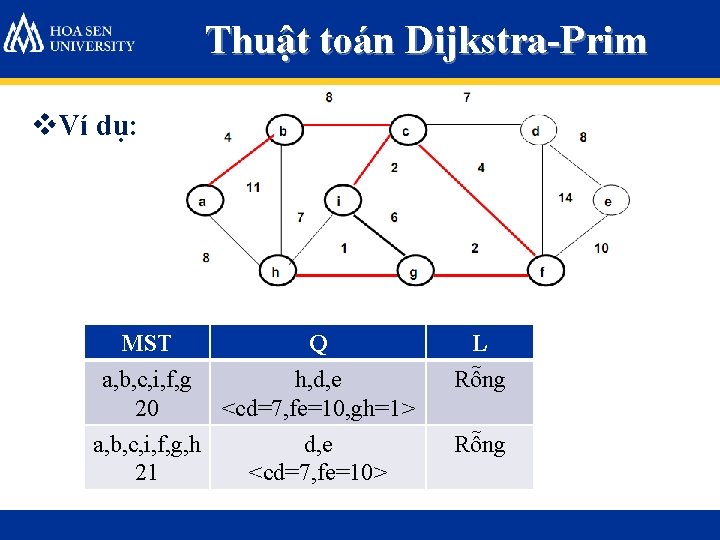
Thuật toán Dijkstra-Prim v. Ví dụ: MST Q L a, b, c, i, f, g 20 h, d, e <cd=7, fe=10, gh=1> Rỗng a, b, c, i, f, g, h 21 d, e <cd=7, fe=10> Rỗng

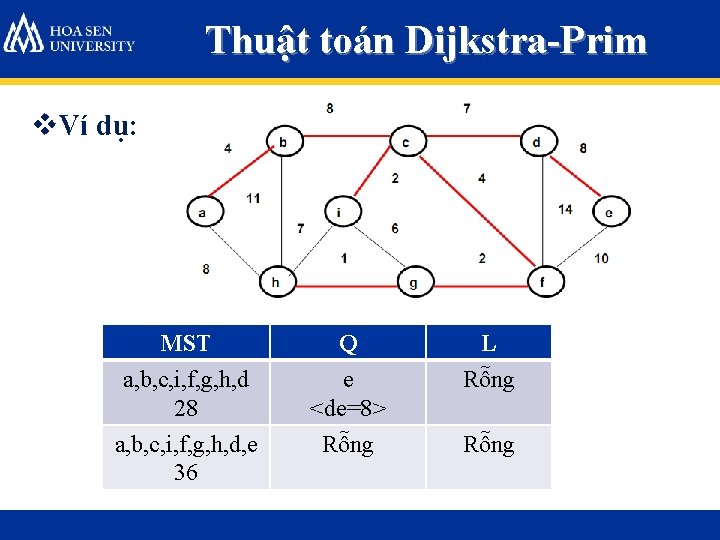
Thuật toán Dijkstra-Prim v. Ví dụ: MST Q L a, b, c, i, f, g, h 21 d, e <cd=7, fe=10> Rỗng a, b, c, i, f, g, h, d 28 e <de=8> Rỗng

Thuật toán Dijkstra-Prim v. Ví dụ: MST Q L a, b, c, i, f, g, h, d 28 e <de=8> Rỗng a, b, c, i, f, g, h, d, e 36 Rỗng

Thuật toán Dijkstra-Prim vĐánh giá giải thuật: - Độ phức tạp của giải thuật Prim phụ thuộc vào cách thực hiện độ ưu tiên ở hàng đợi Q - Nếu Q được thực hiện như một heap nhị phân thì thời gian tính toán của giải thuật là O (E lg. V)

Thuật toán Kruskal v. Giới thiệu: - Khác với giải thuật Dijkstra-Prim bắt đầu với 1 đỉnh bất kì để xây dựng MST. Thuật toán Kruskal tập trung vào các cạnh của đồ thị. v Giải thuật: - Bắt đầu với MST rỗng - Thêm vào MST các cạnh có thứ tự tăng dần theo trọng số cho đến khi tất cả các đỉnh được kết nối

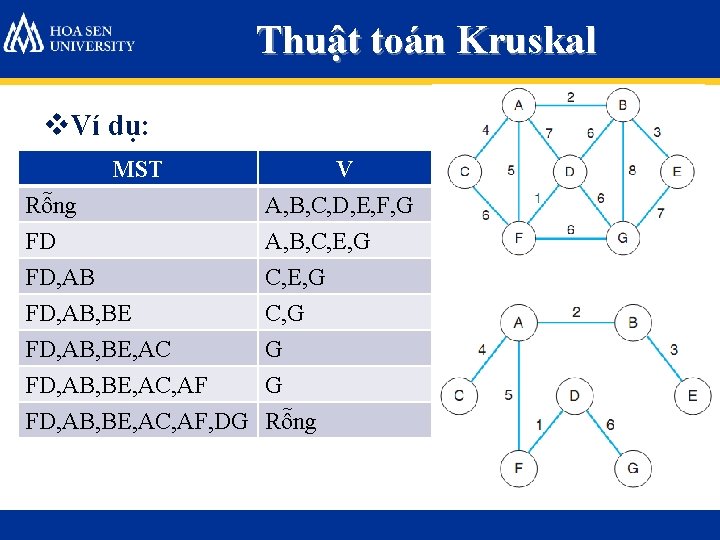
Thuật toán Kruskal v. Ví dụ: MST Rỗng FD FD, AB V A, B, C, D, E, F, G A, B, C, E, G FD, AB, BE, AC, AF, DG C, G G G Rỗng

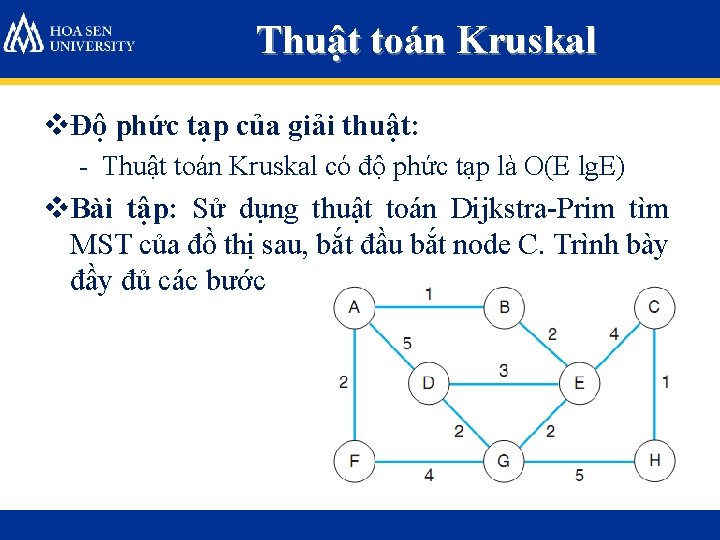
Thuật toán Kruskal vĐộ phức tạp của giải thuật: - Thuật toán Kruskal có độ phức tạp là O(E lg. E) v. Bài tập: Sử dụng thuật toán Dijkstra-Prim tìm MST của đồ thị sau, bắt đầu bắt node C. Trình bày đầy đủ các bước

Thuật toán Kruskal v. Bài tập: Sử dụng thuật toán Krusal tìm MST của đồ thị sau. Trình bày đầy đủ các bước

ĐƯỜNG ĐI NGẮN NHẤT

Đường đi ngắn nhất v. Giới thiệu: Bài toán tìm đường đi ngắn nhất là bài toán quan trọng trong lý thuyết đồ thi. Được ứng dụng trong thực tế: Giao thông, viễn thông… v Bài toán chia làm 2 loại: § Tìm đường đi ngắn nhất giữa 1 cặp đỉnh: Cho 2 đỉnh u, v thuộc G, tìm đường đi ngắn nhất từ u đến v : Dịkstra § Tìm đường đi ngắn nhất giữa tất cả các cặp đỉnh: Tìm đường đi ngắn nhất từ đỉnh u đến đỉnh v, với mọi cặp đỉnh u, v thuộc G: Floyd-Warshall

Giải thuật Dijkstra v. Giới thiệu: - Giải thuật Dijkstra giải bài toán đường đi ngắn nhất nguồn đơn (Single Source Shortest Path) trên một đồ thị có trọng số cạnh đều không âm. - Xác định đường đi ngắn nhất giữa 2 đỉnh a, b cho trước vĐặt vấn đề: Ứng dụng giải thuật cây bao trùm tối thiểu để giải quyết bài toán đường đi ngắn nhất có được không? ? ?

Giải thuật Dijkstra v. Nhận xét: - Giải thuật để giải bài toán MST sẽ không ứng dụng được cho bài toán đường đi ngắn nhất. - Vì sao? ? - Vì vậy cần phải chỉnh sửa giải thuật trên để phù hợp với bài toán đường đi ngắn nhất

Giải thuật Dijkstra v. Giải thuật: - Ở mỗi đỉnh v, giải thuật Dijkstra xác định 3 thông tin: kv, dv, pv • kv = 0 hoặc 1 – xác định trạng thái của đỉnh v ( 0 – chưa chọn, 1 – đã chọn) • dv: Chiều dài đường đi tìm thấy tại thời điểm đang xét từ a đến v • pv: là đỉnh trước của đỉnh v trên đường đi ngắn nhất từ a b. Đường đi ngắn nhất từ a đến b có dạng {a, …, pv, v, …, b}

Giải thuật Dijkstra B 1: Khởi tạo: kv=0, v V; dv= , v V {a}; da=0. B 2: Chọn v V sao cho kv=0 và dv = min {dt / t V, kt=0 } – Nếu dv = thì kết thúc, không tồn tại đường đi từ a b. B 3: Đánh dấu đỉnh v, kv= 1. B 4: Nếu v=b thì kết thúc và db là độ dài đường đi ngắn nhất từ a b. Ngược lại nếu v b sang B 5: Với mỗi đỉnh u kề với v mà ku = 0, kiểm tra Nếu du > dv + w(v, u) thì du= dv + w(v, u) Ghi nhớ đỉnh v: pu: = v. Quay lại B 2.

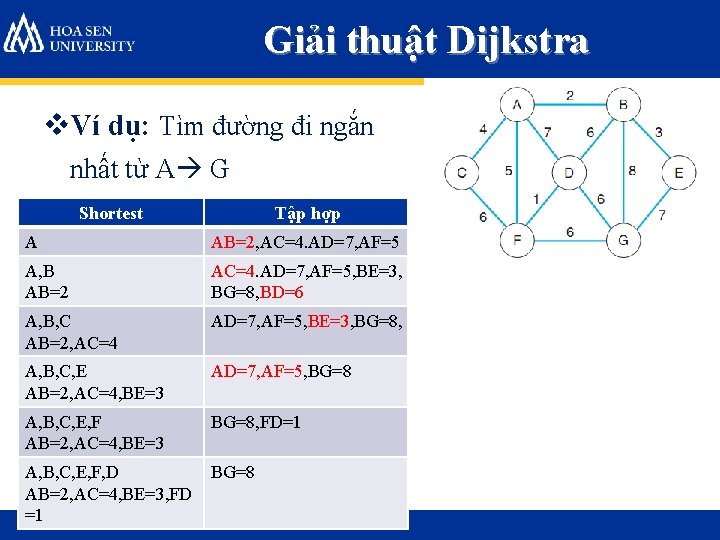
Giải thuật Dijkstra v. Ví dụ: Tìm đường đi ngắn nhất từ A G Shortest Tập hợp A AB=2, AC=4. AD=7, AF=5 A, B AB=2 AC=4. AD=7, AF=5, BE=3, BG=8, BD=6 A, B, C AB=2, AC=4 AD=7, AF=5, BE=3, BG=8, A, B, C, E AB=2, AC=4, BE=3 AD=7, AF=5, BG=8 A, B, C, E, F AB=2, AC=4, BE=3 BG=8, FD=1 A, B, C, E, F, D AB=2, AC=4, BE=3, FD =1 BG=8

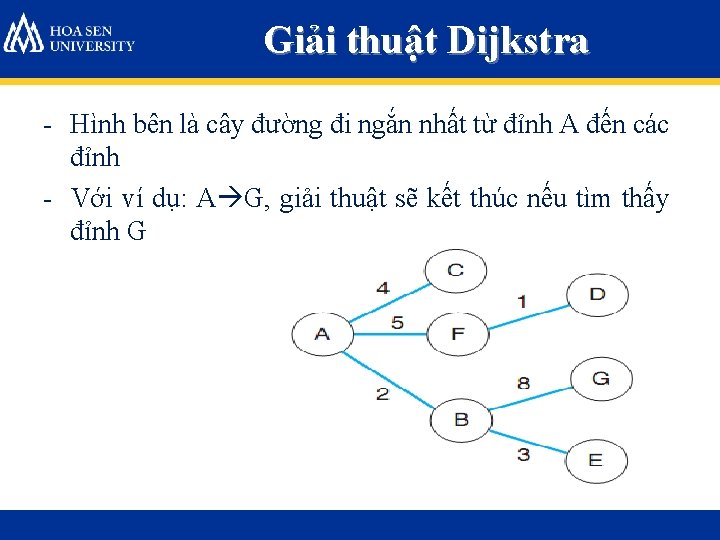
Giải thuật Dijkstra - Hình bên là cây đường đi ngắn nhất từ đỉnh A đến các đỉnh - Với ví dụ: A G, giải thuật sẽ kết thúc nếu tìm thấy đỉnh G

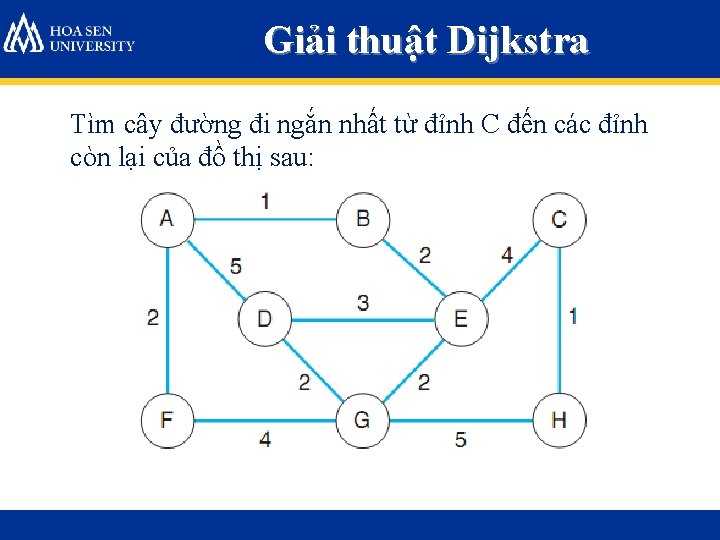
Giải thuật Dijkstra Tìm cây đường đi ngắn nhất từ đỉnh C đến các đỉnh còn lại của đồ thị sau:

Giải thuật Dijkstra vĐộ phức tạp của thuật toán: - Bình thường thuật toán Dijkstra có độ phức tạp O(n 2+m). - Nếu sử dụng cấu trúc heap O((n+m)*log 2(n))

Giải thuật Floyd-Warshall v. Bài toán: Tìm đường đi ngắn nhất của mỗi cặp đỉnh trong đồ thị (All-Pairs Source Shortest Path)