Truthful Mechanism Design for MultiDimensional Scheduling via Cycle

Truthful Mechanism Design for Multi-Dimensional Scheduling via Cycle Monotonicity Ron Lavi Chaitanya Swamy and IE&M, The Technion U. of Waterloo

Job scheduling • n tasks (“jobs”) to be assigned to m workers (“machines”) • Each machine, i, needs pij time units to complete job j. • Our goal: to assign jobs to machines to complete all jobs as soon as possible. More formally: – Let Si denote the set of jobs assigned to machine i, and define the load of a machine: li = j Si pij. – Our goal is then to minimize the maximal load (a. k. a the “makespan” of the schedule).

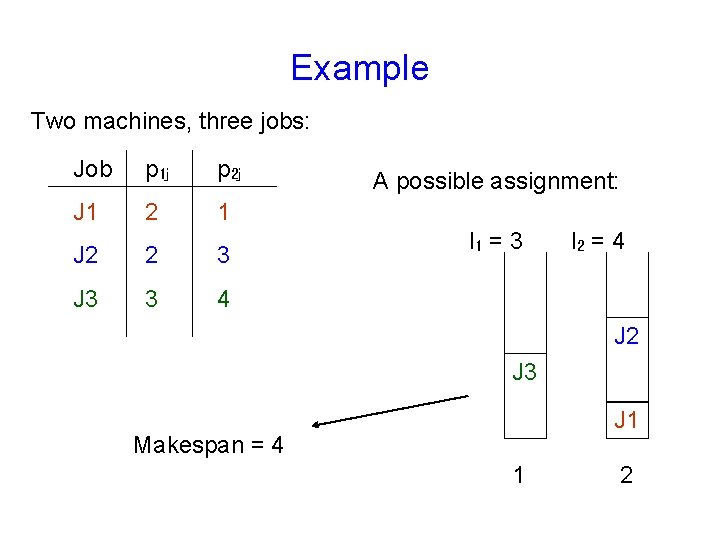
Example Two machines, three jobs: Job p 1 j p 2 j J 1 2 1 J 2 2 3 J 3 3 4 A possible assignment: J 2 J 3 J 1 1 2

Example Two machines, three jobs: Job p 1 j p 2 j J 1 2 1 J 2 2 3 J 3 3 4 A possible assignment: l 1 = 3 l 2 = 4 J 2 J 3 J 1 Makespan = 4 1 2

Scheduling and Mechanism Design • The workers/machines are selfish entities, each one is acting to maximize her individual utility. • If job j is assigned to machine i, it will incur a cost pij for executing the job. • A machine may get a payment, Pi, and its total utility is: Pi - li • Question: design a truthful mechanism (in dominant strategies) that will reach a “close to optimal” makespan. – First raised by Nisan and Ronen (GEB, 2001). – Basic observation: makespan minimization is inherently different than welfare maximization, hence VCG performs poorly (obtains makespan of up to m times the optimum).

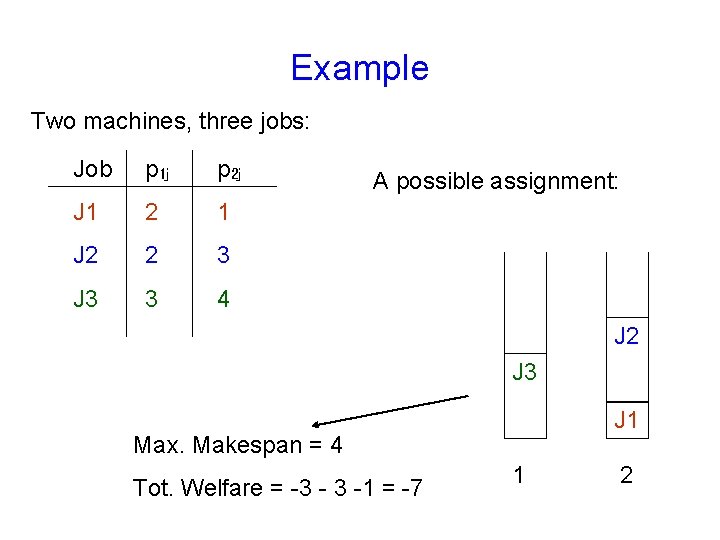
Example Two machines, three jobs: Job p 1 j p 2 j J 1 2 1 J 2 2 3 J 3 3 4 A possible assignment: J 2 J 3 J 1 Max. Makespan = 4 Tot. Welfare = -3 - 3 -1 = -7 1 2

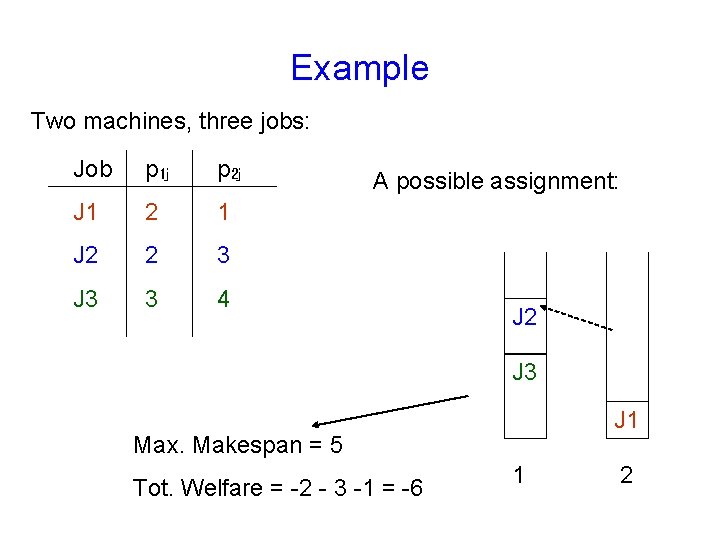
Example Two machines, three jobs: Job p 1 j p 2 j J 1 2 1 J 2 2 3 J 3 3 4 A possible assignment: J 2 J 3 J 1 Max. Makespan = 5 Tot. Welfare = -2 - 3 -1 = -6 1 2

Why is this question important? (1) • Significant to several disciplines: – Computer Science – Operations Research • Makespan minimization is similar to a Rawls’ max-min criteria -- gives a justification from social choice theory. – The implicit goal: assign tasks to workers in a fair manner (rather than in a socially efficient manner). – Can we do it via classic mechanism design?

Why is this question important? (2) • The general status of mechanism design for multidimensional domains is still unclear. – What social choice functions can be implemented? – Few possibilities, few impossibilities, more questions than answers. • Scheduling is a multi-dimensional domain, and is becoming one of the important domains for which we need to determine the possibilities - impossibilities border.

Current status (1) • Nisan and Ronen (1999): a lower bound of 2 for truthful deterministic approximations (regardless of computational issues). – But only give a m-approximation upper bound (VCG) -the gap is very large. • Christodoulou, Koutsoupias, and Vidali (2007): an improved lower bound (about 2. 4). • Mu’alem and Schapira (2007): a 2 -(1/m) lower bound for randomized mechanisms and truthfulness in expectation. • No non-trivial truthful approximation (i. e. o(m)) is known!

Current status (2) • Archer and Tardos (2001) study the special case of related machines: each machine has speed si, and pij = pj/si. – The optimum is implementable (but NP-hard). – Many truthful approximations suggested since. The current-best: a deterministic 3 -approximation by Kovacs (2005). – Also, a truthful PTAS for a fixed number of machines, by Andelman, Azar, and Sorani (2004). • Note: this is a single-dimensional domain, thus it demonstrates again the contrast between single and multi dimensionality.

A multi-dimensional special case • We study a special case of two fixed values: pij {Lj , Hj} – Values are fixed and known to the mechanism. – Still a multi-dimensional domain. – Generalizes the classic “restricted machines” model (pij {pj, }). • Result 1: The optimal allocation is not implementable deterministically. Best possible truthful approximation > 1. 14. – Even when Lj = L, Hj = H – differentiates this case from the related machines case, another consequence of the multi-dimensionality.

Main Results • Result 2: a method to convert any c-approximation algorithm for the two values case to a randomized truthful in expectation mechanism that obtains a 3 c-approximation. – This is not polynomial time • Result 3: (when Lj = L, Hj = H) a deterministic, truthful, and polynomial time, 2 -approximation. • Twist (novelty? ) in analysis: we rely on allocation monotonicity conditions, not on explicit price constructions. – Common for single-dimensional domains (as initiated by Myerson), but not for multi-dimensional domains.

The Randomized Construction: Outline • Description of the monotonicity conditions that are sufficient to obtain truthfulness. • A transition to a fractional domain. • Achieving monotonicity and makespan approximation in the fractional domain. • Rounding the fractional solution.

Truthfulness • Define: – An “alternatives set”, A. In our case, all possible assignments of jobs to machines. – The “type” of a player, ci : A -> R. Here ci is the machine’s load for the given assignment. – Let Vi denote the domain of all valid types. – An algorithm is a function f: V 1 . . . Vn -> A. • A mechanism is a tuple M = (f, P 1 , , Pm ), where Pi : V R is the payment function for player i. • Dfn: Truthful Mechanisms. ci, c-i, c’i : Pi(ci, c-i) - ci(f(ci, c-i)) > Pi(c’i, c-i) - ci(f(c’i , c-i)) • For a given algorithm, how do we check if such prices exist? • Can we come up with an equivalent definition that does not include existential qualifiers, but, rather, only conditions on f.

Weak Monotonicity

Weak monotonicity (W-MON) • DFN (Lavi, Mu’alem, and Nisan ‘ 03, Bikhchandani et. al. ‘ 06): Suppose f(ci, c-i)=a and f(c’i, c-i)=b. Then ci(b) - c’i(b) > ci(a) - c’i(a) • If there exist prices P such that (f, P) is truthful the f must satisfy weak-monotonicity. – If there exist such prices we say that f is implementable. • THM (Saks and Yu, 2005): In convex domains, f is implementable if and only if it is weakly monotone.

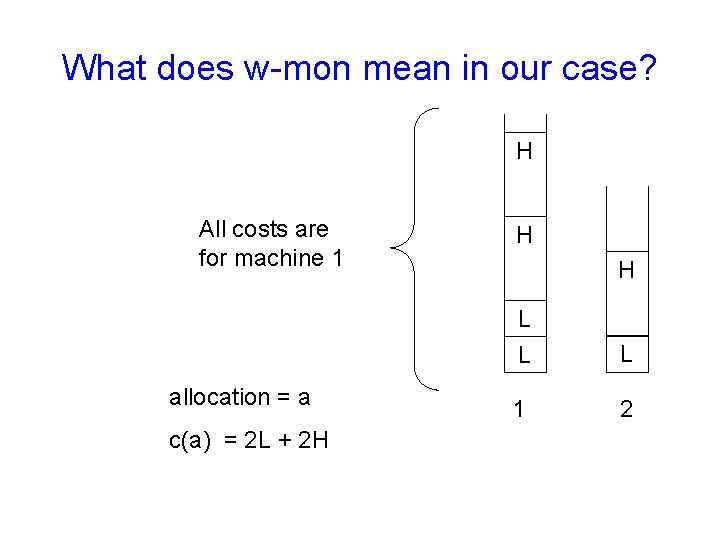
What does w-mon mean in our case? H All costs are for machine 1 allocation = a c(a) = 2 L + 2 H H H L L L 1 2

What does w-mon mean in our case? What happens if machine 1 decreases two jobs to L? allocation = a c(a) = 2 L + 2 H c’(a) = 4 L H L H L L L 1 2

What does w-mon mean in our case? WMON: ci(b) - c’i(b) > ci(a) - c’i(a) = 2(H - L) • What allocations (b) satisfy the inequality? • The only way to get at least 2(H - L) on the left side is to assign the two jobs that were decreased to machine 1. H L H L L L 1 2

What does w-mon mean in our case? And what if an outside job is decreased as well? H L L L 1 H L L 2

What does w-mon mean in our case? WMON: ci(b) - c’i(b) > ci(a) - c’i(a) = 2(H - L) => At least two out of the three jobs that were decreased must be assigned to 1 (doesn’t matter which two, only the numbers matter). H L L L 1 H L L 2

What does w-mon mean in our case? And if one job is increased from L to H? H L H L L 1 H L L 2

What does w-mon mean in our case? WMON: ci(b) - c’i(b) > ci(a) - c’i(a) = (H - L) => If the increased job remains on 1 then two of the jobs that were decreased must be assigned to 1, or alternatively we can “move out” the increased job and keep only one of the decreased jobs. H L H L L 1 H L L 2

What does w-mon mean in our case? H L etc. … You can now see where the monotonicity term comes from. We get an algorithmic condition instead of the game -theoretic definition. H L L 1 H L L 2

Cycle monotonicity • W-MON may be insufficient for implementability in nonconvex domains, like our discrete scheduling domain. • Rochet (1987, JME) describes “cycle monotonicity”, which generalizes W-MON, and is equivalent to implementability on every domain (with finite alternative space). – Gui, Muller, and Vohra (2004) derive prices generically for every cycle-monotone function. – Thus any cycle monotone algorithm can be “automatically” converted to a truthful mechanism. (this can also be done for W-MON algorithms on convex domains). • That’s our way of analysis in the paper. In the talk, I will concentrate on W-MON, for the sake of simplicity.

A fractional solution

Fractional allocations • For the purpose of analysis we consider the case where jobs may be assigned fractionally: – xij denotes the fraction of job j assigned to machine i. – We have i xij = 1 for every j (every job is fully assigned). – The load of machine i is li = j xij pij – Machine i’s value is still minus her load, and her utility is still Pi - li • Cycle monotonicity is still equivalent to truthfulness and we will look for truthful and approximately optimal fractional mechanisms. – This is just an intermediate analysis step. We do not change our actual initial goal.

Fractional conditions for truthfulness • The following condition implies w-mon (easy proof omitted): j, x’ij (pij - p’ij) > xij (pij -p’ij) (where f(pi, p-i) = x and f(p’i, p-i) = x’) • In words: – if pij > p’ij then x’ij > xij – if pij < p’ij then x’ij < xij – if pij = p’ij then no relation between x’ij and xij is required. Corollary: suppose that a fractional algorithm, A, satisfies: Ø pij = Lj => xij > 1/m Ø pij = Hj => xij < 1/m Then A satisfies w-mon.

A fractional algorithm ALG: given any integral allocation, x*, convert it to a fractional allocation x as follows. For every (i, j) s. t. x*ij=1, do: • If pij = Hj then set xij=1/m for any i, j. • If pij = Lj then transfer a fraction 1/m of j from i to every machine i’ with pi’j=Lj.

A fractional algorithm ALG: given any integral allocation, x*, convert it to a fractional allocation x as follows. For every (i, j) s. t. x*ij=1, do: • If pij = Hj then set xij=1/m for any i, j. • If pij = Lj then transfer a fraction 1/m of j from i to every machine i’ with pi’j=Lj. Properties: – W-MON follows from previous lemma. – If x* is c-approx then x is 2 c-approx: each machine gets additional load which is at most the total original load times 1/m, i. e. at most the original makespan. • This converts any algorithm to a truthful fractional mechanism.

Back to Integral Mechanisms

“Rounding” a fractional solution • We will process a fractional assignment xij to a randomized assignment: Xij = random variable, indicates if i gets j. • Lavi and Swamy (2005): given a fractional truthful mechanism, if E[Xij] = xij then there exist prices such that the randomized mechanism is truthful in expectation. • Kumar, Marathe, Parthasarathy, and Srinivasan (2005): given a fractional allocation, one can construct Xij such that – E[Xij]= xij – For every i, (w. p. 1), j Xij pij < j xij pij + maxj: 0 < xij < 1 pij. • In particular, we can take x* to be the optimal allocation. This will give us a 3 -approximation randomized integral mechanism which is truthful in expectation.

Remarks • This has two drawbacks: – It is not polynomial-time – Truthfulness in expectation is weaker than deterministic truthfulness (e. g. requires assuming risk-neutrality). • With all-identical lows and highs: We show a deterministic truthful mechanism, with a better approximation ratio, 2. – Constructions and observations again use cycle monotonicity, but are completely different otherwise. – Proof: uses graph flows, is longer and less straightforward.

Summary • A two-fold motivation for multi-dimensional scheduling: – A natural problem, related to social choice theory, and to classic CS and OR. – Explore in general multi-dimensional mechanism design, and develop new techniques/insights. • We demonstrate how to use W-MON / Cycle-Mon to obtain positive results. • Actual results are for the “two values” case: – A general method to convert any algorithm to a truthful in expectation mechanism with almost the same approx. – A deterministic 2 -approx. truthful mechanism. – OPT is not implementable, best approx > 1. 14. • Open (and seems hard): the case of k>3 fixed values.