Truthful and NearOptimal Mechanism Design via Linear Programming

Truthful and Near-Optimal Mechanism Design via Linear Programming Ron Lavi California Institute of Technology Joint work with Chaitanya Swamy

Overview of the Talk • The model of Combinatorial Auctions – Definition, motivation, challenges and goals, previous results. • Our results – Plus a word on the “big picture”. • Intuition to our construction and proofs

Combinatorial Auctions • m indivisible non-identical items for sale • n bidders compete for subsets of these items • Each bidder i has a valuation for each set of items: vi(S) = value that i assigns to acquiring the set S – vi is non-decreasing (“free disposal”) – v i ( ) = 0 • The multi-unit case: B>1 copies of each item; no player desires more than one copy of each item • Objective: Find a partition of the items (S 1…Sn) that maximizes the social welfare: i vi (Si)

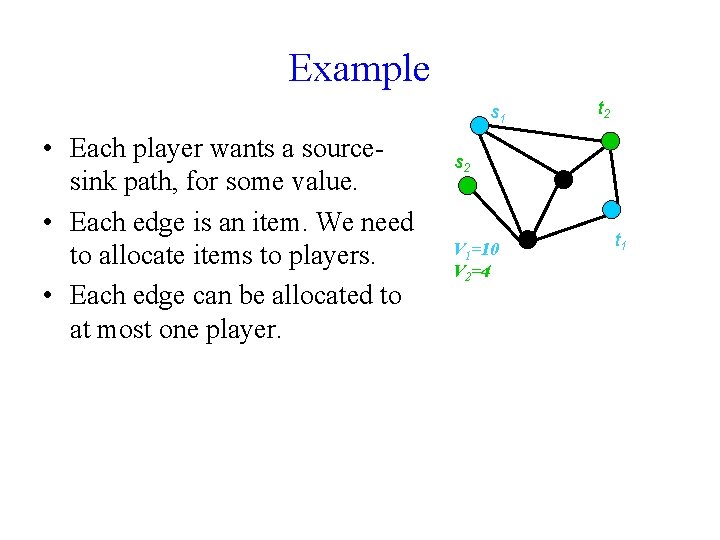
Example s 1 • Each player wants a sourcesink path, for some value. • Each edge is an item. We need to allocate items to players. • Each edge can be allocated to at most one player. t 2 s 2 V 1=10 V 2=4 t 1

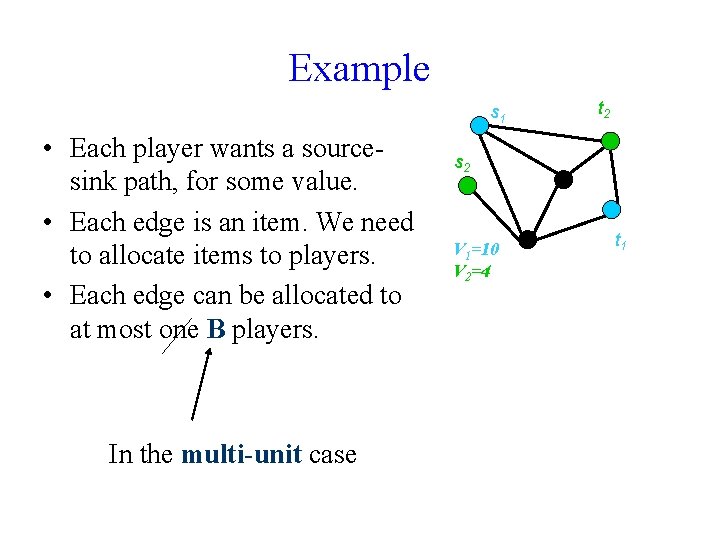
Example s 1 • Each player wants a sourcesink path, for some value. • Each edge is an item. We need to allocate items to players. • Each edge can be allocated to at most one B players. In the multi-unit case t 2 s 2 V 1=10 V 2=4 t 1

Motivation • Abstracts complex resource allocation problems in systems with distributed ownership (scheduling, allocation of network resources). • Real Applications (e. g. the FCC spectrum auction).

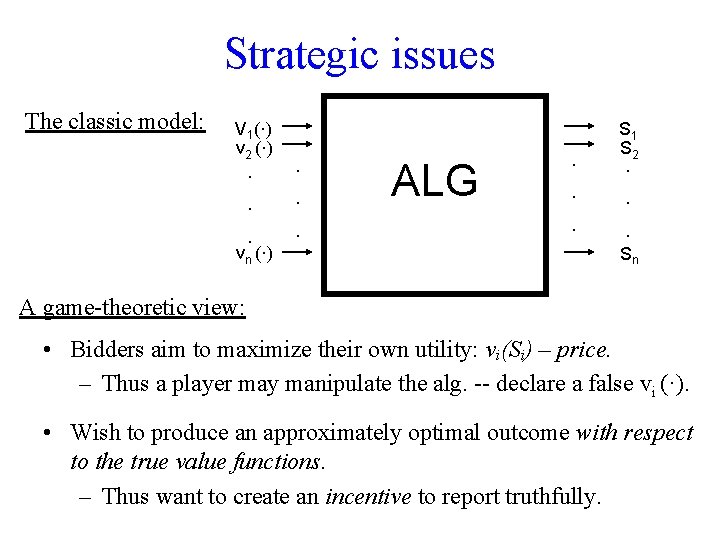
Strategic issues The classic model: V 1(·) v 2 (·) · · · vn (·) ALG · S 1 S 2 · · · Sn A game-theoretic view: • Bidders aim to maximize their own utility: vi(Si) – price. – Thus a player may manipulate the alg. -- declare a false vi (·). • Wish to produce an approximately optimal outcome with respect to the true value functions. – Thus want to create an incentive to report truthfully.

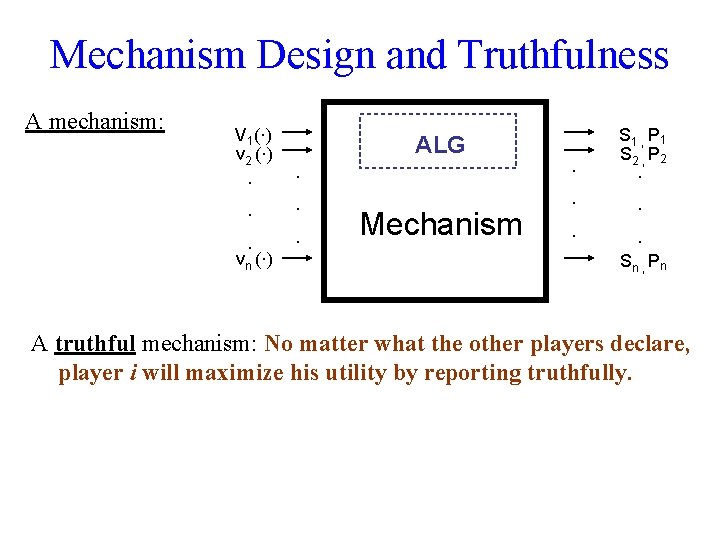
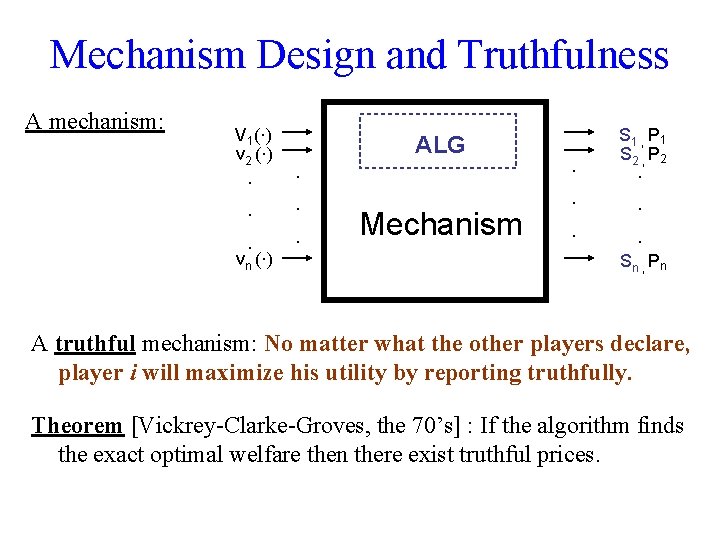
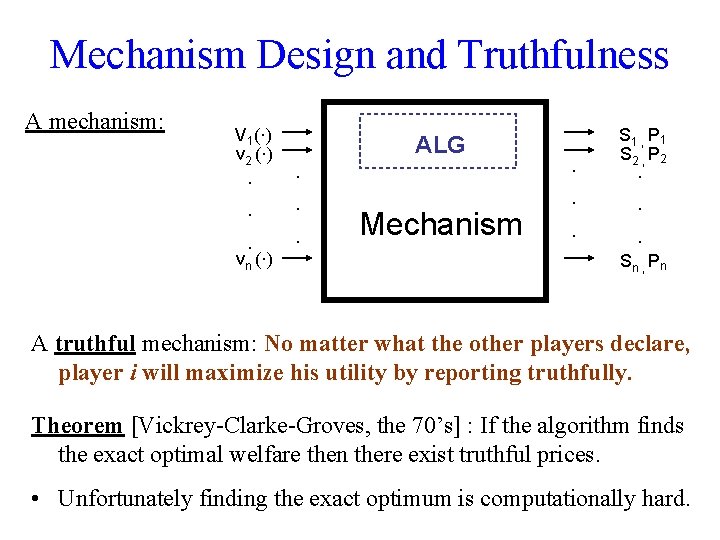
Mechanism Design and Truthfulness A mechanism: V 1(·) v 2 (·) · · · S 1 , P 1 S 2 , P 2 · · · · · vn (·) ALG Mechanism Sn , Pn A truthful mechanism: No matter what the other players declare, player i will maximize his utility by reporting truthfully.

Mechanism Design and Truthfulness A mechanism: V 1(·) v 2 (·) · · · S 1 , P 1 S 2 , P 2 · · · · · vn (·) ALG Mechanism Sn , Pn A truthful mechanism: No matter what the other players declare, player i will maximize his utility by reporting truthfully. Theorem [Vickrey-Clarke-Groves, the 70’s] : If the algorithm finds the exact optimal welfare then there exist truthful prices.

Mechanism Design and Truthfulness A mechanism: V 1(·) v 2 (·) · · · S 1 , P 1 S 2 , P 2 · · · · · vn (·) ALG Mechanism Sn , Pn A truthful mechanism: No matter what the other players declare, player i will maximize his utility by reporting truthfully. Theorem [Vickrey-Clarke-Groves, the 70’s] : If the algorithm finds the exact optimal welfare then there exist truthful prices. • Unfortunately finding the exact optimum is computationally hard.

Complexity Issues • Communication: input is exponential (in m). – No algorithm can approximate better than m 1/(B+1) with polynomial communication [Nisan; Nisan and Segal; Dobzinski and Schapira] • Computation: – It is NP-hard to approximate better than m 1/(B+1), even for short valuations [Lehmann, O'Callaghan, Shoham; Bartal, Gonen, Nisan] • There exist polynomial time O(m 1/(B+1))-approximations – In particular when B=Ω(log m) there exists a (1+ε)approximation

We seek truthful and computationally feasible mechanisms. In other words, are there other ways to embed truthfulness into a given algorithm?

Previous attempts for resolution • The “single minded” case : – √m approx. when B=1 [Lehmann, O'Callaghan, Shoham] – (1+ε)-approx. when B=Ω(log m) [Archer, Papadimitriou, Talwar, Tardos] – O(m 1/B) -approx. for any B [Briest, Krysta, Vocking] • For general valuations: – O(B·m 1/B-2) for B>3 – O(√m) for B=1 [Bartal, Gonen, Nisan] [Dobzinski, Nisan, Schapira] • Bundling equilibria in VCG to reduce communication (essentially a negative result). [Holzman, Kfir-Dahav, Monderer, Tennenholtz] • No result for the general case; a large gap from the best approximability results for the non-single minded case.

Our results Main construction: Given any alg. for general CA that also bounds the integrality gap of the LP relaxation, one can construct a randomized, truthful in expectation, mechanism that has the same approx. ratio. Immediate Applications: strategic mechanisms with approximation guarantees that match the best known non-strategic ones: – A strategic O(m 1/B+1) approx. for general valuations and any B. – If B=Ω(log m) this yields a (1+ε)-approx. mechanism. – This technique applies to other “packing domains”, for example multi-parameter knapsack problems. • By moving from deterministic to randomized mechanisms, we completely close the strategic -- non-strategic gap for general CAs.

Truthfulness in expectation [Archer and Tardos] : No matter what the other players declare, player i will maximize his expected utility by reporting truthfully. • A worst case notion (the distribution is created by the mechanism, not assumed on the input). • A player need not assume anything about the rationality of others. • This implicitly implies, however, that a player is risk-neutral. – Thus weaker than deterministic truthfulness.

An aside – a more general view • Does deterministic truthfulness can yield such results? – For B=1, any deterministic mechanism that is also IIA cannot obtain a reasonable approximation [Lavi, Mu’alem, Nisan] • Other GT notions might yield distribution-free/worst-case results? – “Rationalizable strategies” for single-item first price auctions [Dekel and Wolinsky, Battigalli and Siniscalchi] – “Set-Nash” for online auctions [Lavi and Nisan] – “Implementation in undominated strategies” for single-value combinatorial auctions [Babaioff, Lavi, Pavlov] – What else?

More on VCG Truthfulness : vi, v-i, v’i : vi(f(vi, v-i)) – pi(vi, v-i) > vi(f(v’i , v-i)) – pi (v’i, v-i) Theorem [Vickrey-Clarke-Groves] : If the algorithm finds the exact optimal welfare then there exist truthful prices. The prices: If (s 1, …, sn) is the optimal allocation according to the reported types v=(v 1, …, vn), set prices to pi(v) = -Σj≠ivj(sj) + hi(v-i) Proof: Suppose a player says v’i and the chosen allocation is (s’ 1, …, s’n). His utility is vi(s’i) - pi(v’i, v-i) = vi(s’i) + Σj≠ivj(s’j) < vi(si) + Σj≠ivj(sj) = vi)si - (pi)vi, v-i ( i. e. telling his true value would weakly improve his utility.

The fractional case • xi, s is the fraction of bundle S that player i gets. • The fractional case is easy to solve by an LP: • Thus we can use VCG for this case.

The fractional case • xi, s is the fraction of bundle S that player i gets. • The fractional case is easy to solve by an LP: For every c>1 • Thus we can use VCG in this case as well.

The fractional case • xi, s is the fraction of bundle S that player i gets. • The fractional case is easy to solve by an LP: For every c>1 • Thus we can use VCG in this case as well.

More on solving the LP • “Short” valuations (the LP is succinctly describable) – We have a (one shot) truthful in expectation mechanism. – For example k-minded players. The first strategic mechanism for this case. • General valuations: the LP is efficiently solvable with a “demand oracle” [Blumrosen-Nisan] – We have an iterative mechanism; truthfulness in expectation is ex-post Nash equilibrium. – The first strategic mechanism with polynomial communication, computation, and tight approximation bounds.

A randomized truthful integral mechanism Construction: 1. Compute a fractional solution x* (optimal w. r. t. the declared values). 2. Decompose x*/c = λ 1·x 1+…+ λL·x. L where {xl}l are the integral solutions, and λ 1 +…+ λL = 1. The main technical construction. Works if c is the integrality gap, and if furthermore we have an algorithm that “verifies” this. For this we extend a technique of [Carr and Vempala].

A randomized truthful integral mechanism Construction: 1. Compute a fractional solution x* (optimal w. r. t. the declared values). 2. Decompose x*/c = λ 1·x 1+…+ λL·x. L where {xl}l are the integral solutions, and λ 1 +…+ λL = 1. 3. Choose xl with probability λ 1 and set the expected price to be the VCG price in the fractional setting. Claim: This is truthful in expectation

A randomized truthful integral mechanism Construction: 1. Compute a fractional solution x* (optimal w. r. t. the declared values). 2. Decompose x*/c = λ 1·x 1+…+ λL·x. L where {xl}l are the integral solutions, and λ 1 +…+ λL = 1. 3. Choose xl with probability λ 1 and set the expected price to be the VCG price in the fractional setting. Claim: This is truthful in expectation Proof: Suppose that vi y* and v’i z*. We have: vi(y*/c) – pi(vi, v-i) > vi(z*/c) – pi (v’i, v-i) As the fractional mechanism is truthful

A randomized truthful integral mechanism Construction: 1. Compute a fractional solution x* (optimal w. r. t. the declared values). 2. Decompose x*/c = λ 1·x 1+…+ λL·x. L where {xl}l are the integral solutions, and λ 1 +…+ λL = 1. 3. Choose xl with probability λ 1 and set the expected price to be the VCG price in the fractional setting. Claim: This is truthful in expectation Proof: Suppose that vi y* and v’i z*. We have: vi(y*/c) – pi(vi, v-i) > vi(z*/c) – pi (v’i, v-i) y y [λ 1·vi(x 1)+…+ λ L·vi(x. L)] – pi(vi, v-i) > [λz 1·vi(x 1)+…+ λz. L·vi(x. L)] – pi (v’i, v-i) By the decomposition

A randomized truthful integral mechanism Construction: 1. Compute a fractional solution x* (optimal w. r. t. the declared values). 2. Decompose x*/c = λ 1·x 1+…+ λL·x. L where {xl}l are the integral solutions, and λ 1 +…+ λL = 1. 3. Choose xl with probability λ 1 and set the expected price to be the VCG price in the fractional setting. Claim: This is truthful in expectation Proof: Suppose that vi y* and v’i z*. We have: vi(y*/c) – pi(vi, v-i) > vi(z*/c) – pi (v’i, v-i) [λy 1·vi(x 1)+…+ λy. L·vi(x. L)] – pi(vi, v-i) > [λz 1·vi(x 1)+…+ λz. L·vi(x. L)] – pi (v’i, v-i) By construction E[ vi(f(vi, v-i)) – pi(vi, v-i) ] > E[ vi(f(v’i , v-i)) – pi (v’i, v-i) ]

The decomposition (1) Claim: Given a c-approx. algorithm to the optimal fractional solution, one can decompose any fractional point x*/c to a convex combination of integral points, i. e. x*/c = λ 1·x 1+…+ λL·x. L (where xl is integral), in polynomial time. Remark: The alg. should “work” for any weights {wi, s} Method (based on [Carr and Vempala]):

The decomposition (1) Claim: Given a c-approx. algorithm to the optimal fractional solution, one can decompose any fractional point x*/c to a convex combination of integral points, i. e. x*/c = λ 1·x 1+…+ λL·x. L (where xl is integral), in polynomial time. Remark: The alg. should “work” for any weights {wi, s} Method (based on [Carr and Vempala]): x wi, s xz

The decomposition (2) Observation: If (wi, s , z) is feasible then

The decomposition (2) Observation: If (wi, s , z) is feasible then Proof: Suppose o/w. (1/c) Σi, s x*i, s · wi, s > 1 - z

The decomposition (2) Observation: If (wi, s , z) is feasible then Proof: Suppose o/w. Using A, find xl s. t. Σi, s wi, s · xli, s > (1/c) Σi, s x*i, s · wi, s > 1 - z contradicting feasibility.

The decomposition (2) Observation: If (wi, s , z) is feasible then Proof: Suppose o/w. Using A, find xl s. t. Σi, s wi, s · xli, s > (1/c) Σi, s x*i, s · wi, s > 1 - z contradicting feasibility. Implications: 1. The optimal solution is 1, as we need.

The decomposition (2) Observation: If (wi, s , z) is feasible then Proof: Suppose o/w. Using A, find xl s. t. Σi, s wi, s · xli, s > (1/c) Σi, s x*i, s · wi, s > 1 - z contradicting feasibility. Implications: 1. The optimal solution is 1, as we need. 2. We can use the ellipsoid method to find it in polynomial time: • A separation oracle is implemented as above. • This yields a dual program of polynomial size. Its dual will give us the convex decomposition.

Summary • Studied the clash between computational and game-theoretic considerations. • For a variety of domains, we give a technique to embed truthfulness in existing algorithmic methods, via randomization and Linear Programming. • Our technique closes the existing large approximation gaps in the literature, providing several new and tight results. – CAs, multi-parameter knapsack problems, Routing and flow problems. • Still open: – Deterministic truthfulness in CAs. – Truthfulness for special cases of CAs (e. g. sub-modularity of value functions). – Other methods for truthful constructions?