Truth Tables Hurley 6 2 6 4 Concepts

Truth Tables Hurley 6. 2 - 6. 4

Concepts • Truth function • Logically equivalent • Truth Table • Contradictory • Truth value assignment • Consistent • Tautologous • Inconsistent • Self-contradictory • Valid • Contingent • Invalid

How to… • Determine the truth value of a whole sentence given the truth value of its parts • Use truth tables to test – Sentences for tautolgousness, self-contradiction or contingency – Pairs of sentences for equivalence or contradiction – Sets of sentences for consistency or inconsistency – Arguments for validity or invalidity • Determine validity and invalidity from information about premises and conclusion

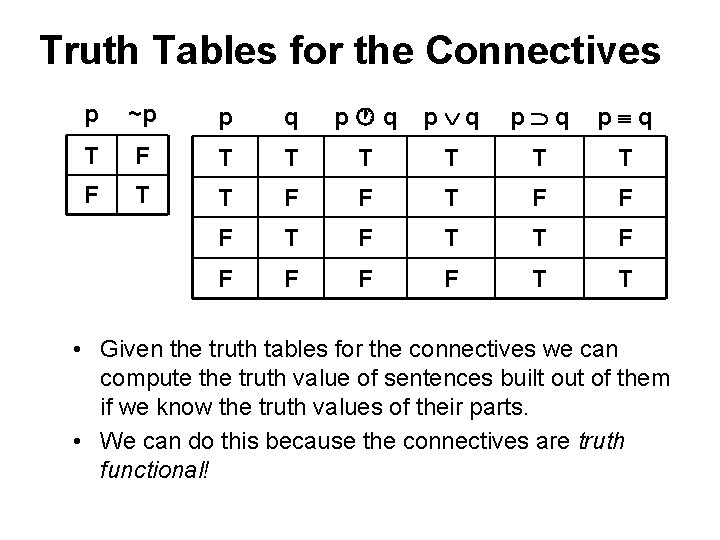
Truth Tables for the Connectives p ~p p q p q p q T F T T F F F T T • Given the truth tables for the connectives we can compute the truth value of sentences built out of them if we know the truth values of their parts. • We can do this because the connectives are truth functional!

Truth Value Assignment • Each row of a truth table represents a truth value assignment: an assignment of ‘T’ or ‘F’ to each sentence letter where same sentence letters get same truth value. • When you compute the truth value of a sentence given truth values for its parts you’re computing truth value for the sentence in one truth value assignment. • When you do a complete truth table for a sentence, set of sentence or argument you’re computing truth value in every possible truth value assignment.

Truth Table Tests Sentences Pairs of sentences • Tautologous • Equivalent • Self-contradictory • Contingent • Neither Set of sentences Arguments • Consistent • Valid • Inconsistent • Invalid

Sentences • Tautology (tautologous sentence) – Necessarily true – True in every truth value assignment • Self-contradictory sentence – Necessarily false – False in every truth value assignment • Contingent sentence – Neither necessarily true nor necessarily false – True in some truth value assignments, false in others

Testing Sentences for Tautologousness • Write the sentence ~ P (Q P)

Testing Sentences for Tautologousness • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) ~ P (Q P)

Testing Sentences for Tautologousness • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it ~ P (Q P) Now we need to assign truth values to each sentence letter on each row of the column underneath it. We assign these truth values according to a standard pattern.

Why? And what pattern? • We want the truth table to display all possible truth value assignments for the sentence letters without duplicating any so we adopt a convention to guarantee that. • The column under the first sentence letter gets half true, half false; the column under the second sentence letter has half true, half false for rows where the first is true and half true, half false for rows where the first is false; the column under the third subdivides in the same way, and so on.

Etc… The column for the first type letter is half T and half F, the second subdivides that, the third subdivides the second, and so on. . . 1 2 T F T T F F We don’t give you great big truth tables on tests because we have to grade them! 3 T F T T F F 4 T T F F T F T F T T T T F F F F T T F F T F T F

Testing Sentences for Tautologousness • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. ~ P T T F F (Q P)

Testing Sentences for Tautologousness • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. ~ P (Q P) T T F F

Testing Sentences for Tautologousness • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. ~ P (Q P) T T F T F F Now we’ve assigned truth values to all the sentence letters and are ready to compute truth values for the whole sentence working from smaller to larger subformulas.

Testing Sentences for Tautologousness • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. Compute truth values ~ P (Q P) T T F T F F We want truth values for ~ P in the column under its main connective. We’ll compute them from the truth values under P given the truth table for negation.

Testing Sentences for Tautologousness • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. Compute truth values (Q ~ P F T T T F T F T F F F Got it! The truth values for ~ P are in the column under its main connective. P)

Testing Sentences for Tautologousness • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. Compute truth values (Q ~ P P) F T T T F T F T F F F Now we want to computer truth values for Q P so we’ll look at the truth values for its antecedent and consequent.

Testing Sentences for Tautologousness • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. Compute truth values (Q ~ P F T T T F F T F We’ve computed truth values for Q P and now have what we need to compute truth values for the whole sentence we’re testing P)

Testing Sentences for Tautologousness • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. Compute truth values (Q ~ P P) F T T T F F T F At last we can compute truth values for ~P (Q P)! To do that we look at the truth values for ~P and Q P, which are under their main connectives.

Testing Sentences for Tautologousness • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. Compute truth values ~ P (Q F T T T F F T F T F Now we have truth values for ~P (Q P) in the main column of the truth table--the boxed column under the main connective. P)

Testing Sentences for Tautologousness • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. Compute truth values Read down the main column ~ P (Q F T T T F F T F T F P) The truth table is complete! Now we just have to read down the main column to determine whether the sentence is tautologous, selfcontradictory or contingent.

Testing Sentences for Tautologousness • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. Compute truth values Read down main column: – Tautologous: all T – Self-contradictory: all F – Contingent: neither all T nor all F ~ P (Q F T T T F F T F T F P)

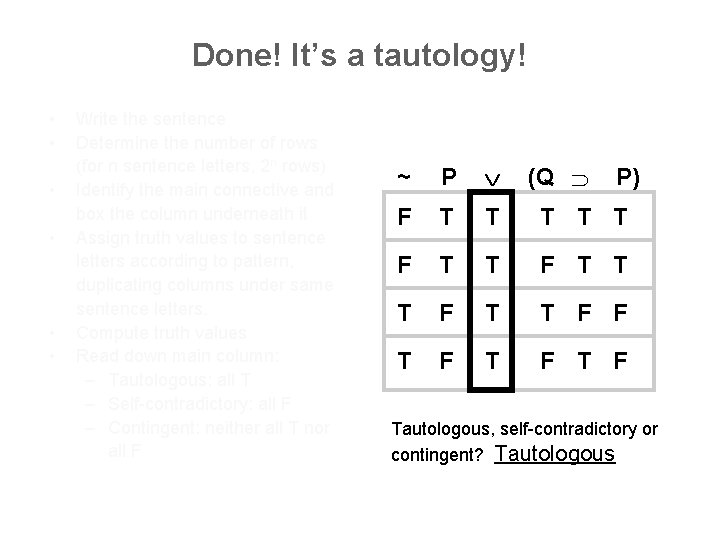
Done! It’s a tautology! • • • Write the sentence Determine the number of rows (for n sentence letters, 2 n rows) Identify the main connective and box the column underneath it Assign truth values to sentence letters according to pattern, duplicating columns under same sentence letters. Compute truth values Read down main column: – Tautologous: all T – Self-contradictory: all F – Contingent: neither all T nor all F ~ P (Q F T T T F F T F T F P) Tautologous, self-contradictory or contingent? Tautologous

Pairs of Sentences • Equivalent – Necessarily have same truth value – Have same truth value in every truth value assignment • Contradictory – Necessarily have opposite truth value – Have opposite truth value in every truth value assignment • Neither – Neither equivalent nor contradictory

Testing Pairs of Sentences for Equivalence • Write the sentences side by side with a slash between them. ~ (P Q) / ~ P ~ Q

Testing Pairs of Sentences for Equivalence • • Write the sentences side by side with a slash between them. Determine the number of rows for number of sentence letters in both sentences. ~ (P Q) / ~P ~ Q

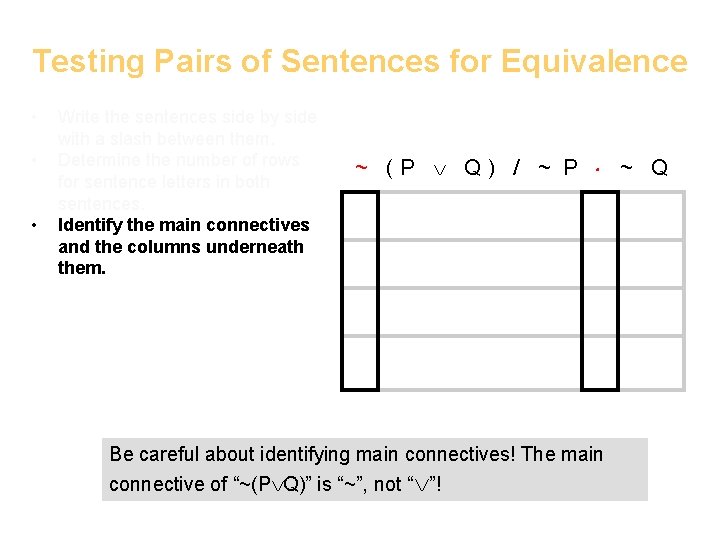
Testing Pairs of Sentences for Equivalence • • • Write the sentences side by side with a slash between them. Determine the number of rows for sentence letters in both sentences. Identify the main connectives and the columns underneath them. ~ (P Q) / ~ P ~ Q Be careful about identifying main connectives! The main connective of “~(P Q)” is “~”, not “ ”!

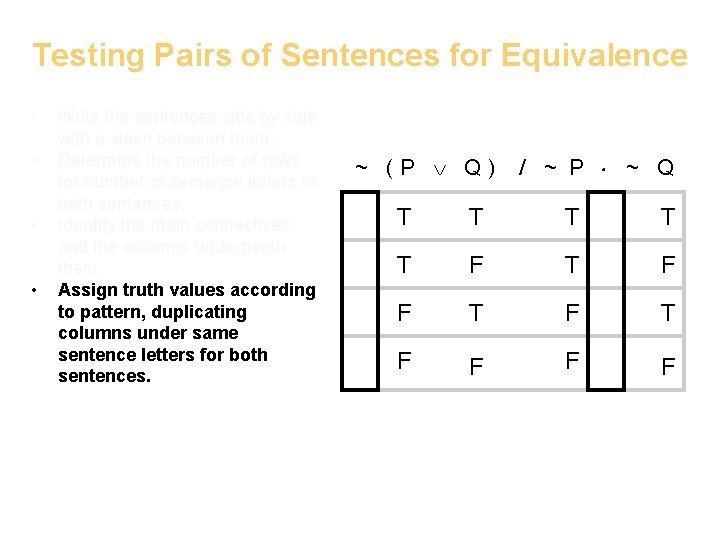
Testing Pairs of Sentences for Equivalence • • Write the sentences side by side with a slash between them. Determine the number of rows for number of sentence letters in both sentences. Identify the main connectives and the columns underneath them. Assign truth values according to pattern, duplicating columns under same sentence letters for both sentences. ~ (P Q) / ~ P ~ Q T T T F T F F F F

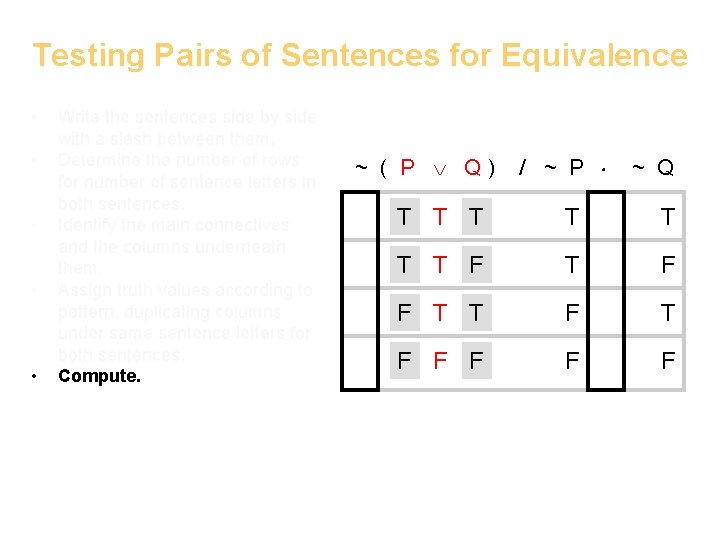
Testing Pairs of Sentences for Equivalence • • • Write the sentences side by side with a slash between them. Determine the number of rows for number of sentence letters in both sentences. Identify the main connectives and the columns underneath them. Assign truth values according to pattern, duplicating columns under same sentence letters for both sentences. Compute. ~ ( P Q) / ~ P ~ Q T T T T F F F

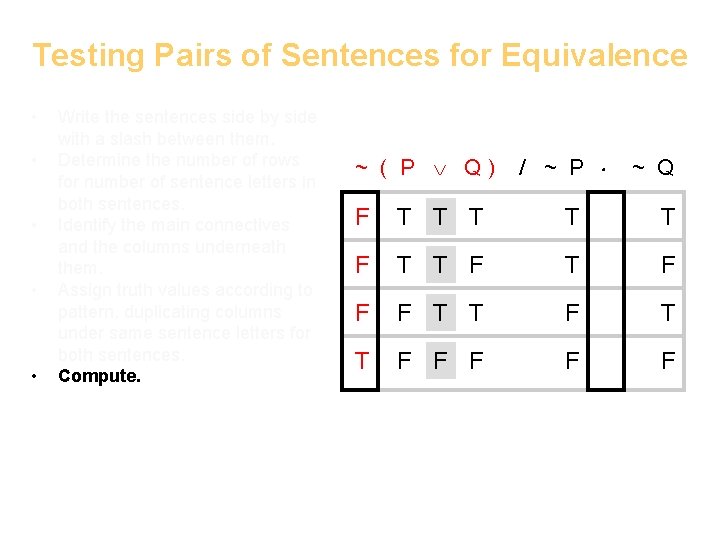
Testing Pairs of Sentences for Equivalence • • • Write the sentences side by side with a slash between them. Determine the number of rows for number of sentence letters in both sentences. Identify the main connectives and the columns underneath them. Assign truth values according to pattern, duplicating columns under same sentence letters for both sentences. Compute. ~ ( P Q) / ~ P ~ Q F T T T F T F F F T T F F F

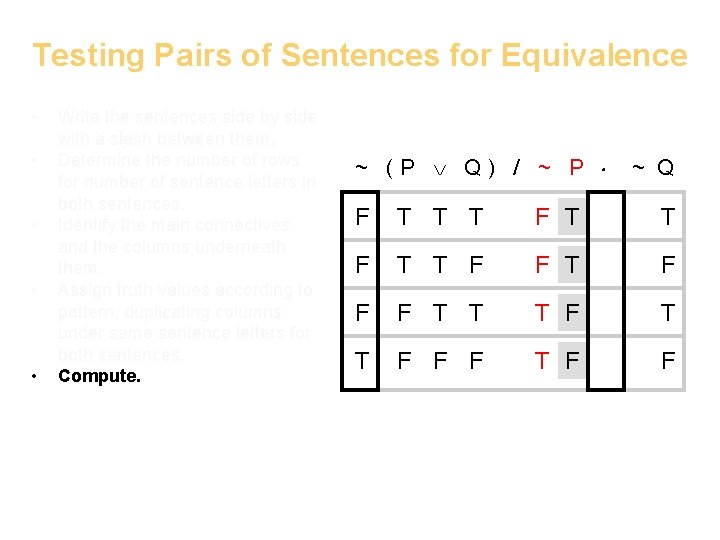
Testing Pairs of Sentences for Equivalence • • • Write the sentences side by side with a slash between them. Determine the number of rows for number of sentence letters in both sentences. Identify the main connectives and the columns underneath them. Assign truth values according to pattern, duplicating columns under same sentence letters for both sentences. Compute. ~ (P Q) / ~ P ~ Q F T T T F F F T T T F F F T F F

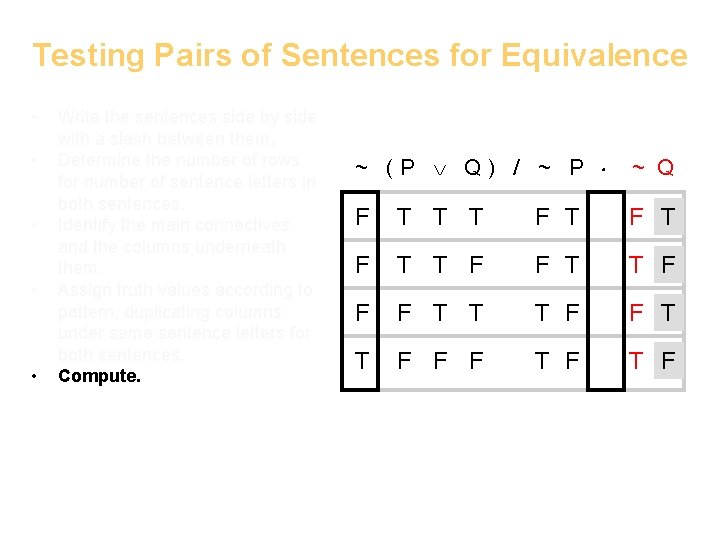
Testing Pairs of Sentences for Equivalence • • • Write the sentences side by side with a slash between them. Determine the number of rows for number of sentence letters in both sentences. Identify the main connectives and the columns underneath them. Assign truth values according to pattern, duplicating columns under same sentence letters for both sentences. Compute. ~ (P Q) / ~ P ~ Q F T T T F T F T T F F F T F

Testing Pairs of Sentences for Equivalence • • • Write the sentences side by side with a slash between them. Determine the number of rows for number of sentence letters in both sentences. Identify the main connectives and the columns underneath them. Assign truth values according to pattern, duplicating columns under same sentence letters for both sentences. Compute. ~ ( P Q) / ~ P ~ Q F T T T F F T F F F T T T F F F T F T T F

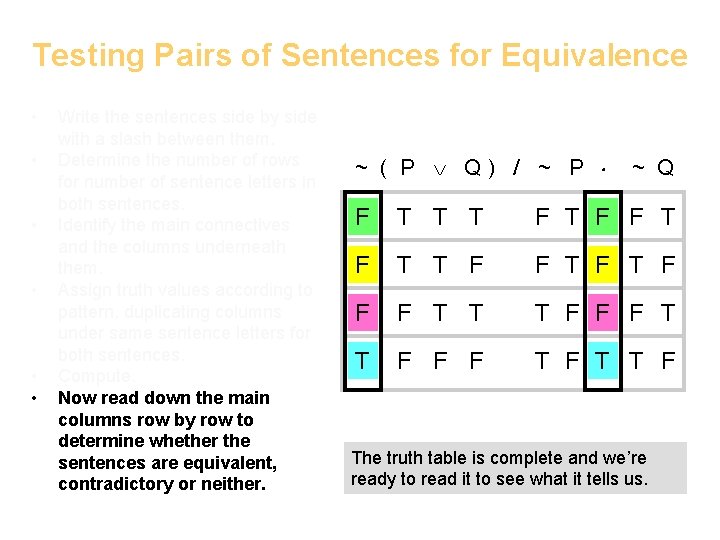
Testing Pairs of Sentences for Equivalence • • • Write the sentences side by side with a slash between them. Determine the number of rows for number of sentence letters in both sentences. Identify the main connectives and the columns underneath them. Assign truth values according to pattern, duplicating columns under same sentence letters for both sentences. Compute. Now read down the main columns row by row to determine whether the sentences are equivalent, contradictory or neither. ~ ( P Q) / ~ P ~ Q F T T T F F T F F F T T T F F F T F The truth table is complete and we’re ready to read it to see what it tells us.

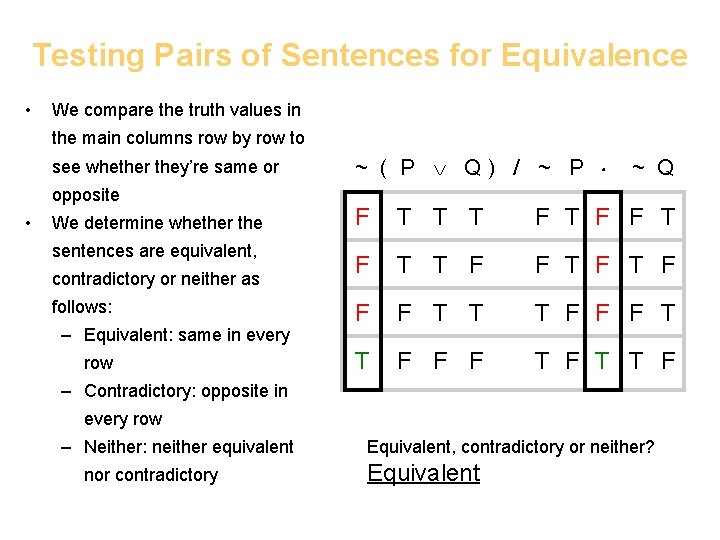
Testing Pairs of Sentences for Equivalence • We compare the truth values in the main columns row by row to see whether they’re same or opposite • We determine whether the sentences are equivalent, contradictory or neither as follows: – Equivalent: same in every row ~ ( P Q) / ~ P ~ Q F T T T F F T F F F T T T F F F T F T T F – Contradictory: opposite in every row – Neither: neither equivalent nor contradictory Equivalent, contradictory or neither? Equivalent

Sets of Sentences • Consistent – They can all be true together – There is some truth value assignment that makes all of the sentences true • Inconsistent – Not consistent: they can’t all be true together – There is no truth value assignment that makes all of the sentences true

Testing Sets of Sentences for Consistency Any one of them could win…but they can’t all win.

Testing Sets of Sentences for Consistency P Q / ~ P Q / Q T T T F F F F T T T F T F F • Do the truth table for the sentences in the usual way • We want to see whethere’s a truth value assignment that makes all the sentences true • If there is, the set of sentences is consistent. • If there isn’t, the set of sentences is inconsistent.

Testing Sets of Sentences for Consistency P Q / ~ P Q / Q T T T F F F F T T T F T F F • We read across the main columns row by row • Each row represents a truth value assignment • If there’s a row in which all main columns have T the set of sentences is consistent. • If there’s no row in which all main columns have T the set of sentences is inconsistent.

Testing Sets of Sentences for Consistency P This row shows consistency Q / ~ P Q / Q T T T F F F F T T T F T F F Consistent or inconsistent? This row doesn’t show anything! Consistent We talk about sets of sentences being consistent or inconsistent. We don’t talk about rows of a truth table being consistent or inconsistent--that makes no sense!

Testing Sets of Sentences for Consistency P Q / P ~ Q / Q T T F FT T T F F T T TF F F T T F F FT T F F F TF F Consistent or inconsistent? Inconsistent Suppose things were a little different… Now there’s no row where all main columns get T so this set of sentences is inconsistent!

Arguments • Valid – It’s not logically possible for all the premises to be true and the conclusion false – There is no truth value assignment that makes all the premises true and the conclusion false. • Invalid – Not valid. – There is some truth value assignment that makes all the premises true and the conclusion false

Testing Arguments for Validity P Q • Q / ~ Q // P � T T T F F T T F T F T F F Do the truth table with slashes between premises and a double slash between the last premise and the conclusion • We want to see whethere’s a truth value assignment that makes all the premises true and the conclusion false • If there is, the argument is invalid. • If there isn’t, the argument is valid.

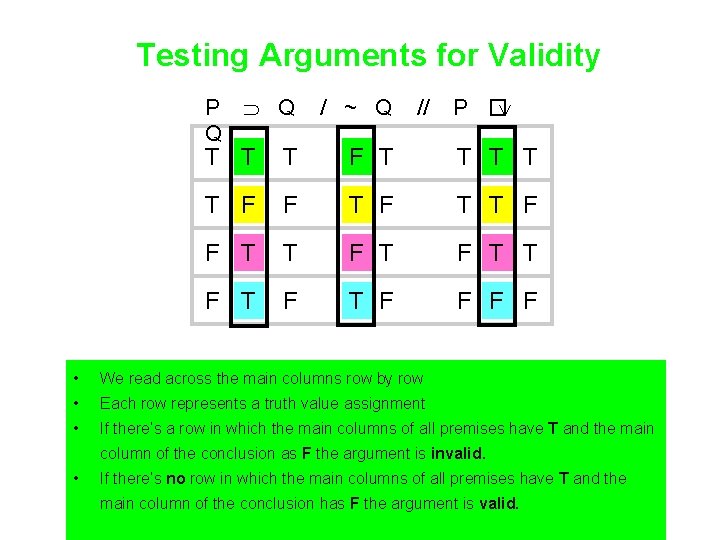
Testing Arguments for Validity P Q Q / ~ Q // P � T T T F F T T F T F T F F • We read across the main columns row by row • Each row represents a truth value assignment • If there’s a row in which the main columns of all premises have T and the main column of the conclusion as F the argument is invalid. • If there’s no row in which the main columns of all premises have T and the main column of the conclusion has F the argument is valid.

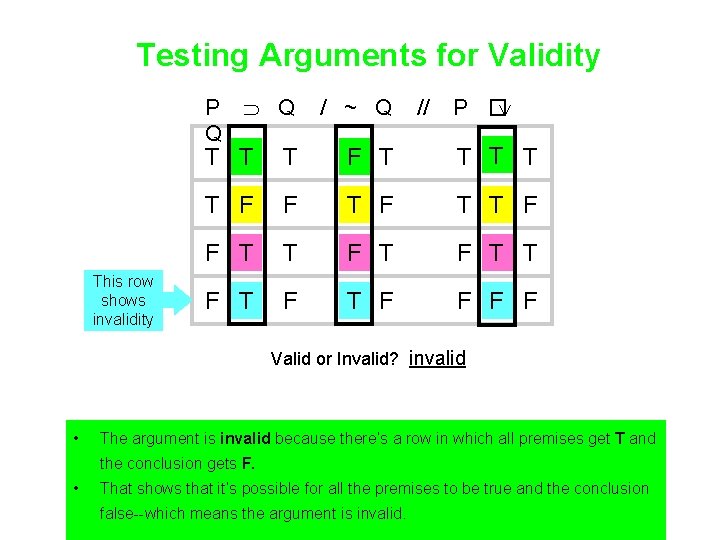
Testing Arguments for Validity P Q This row shows invalidity Q / ~ Q // P � T T T F F T T F T F T F F Valid or Invalid? invalid • The argument is invalid because there’s a row in which all premises get T and the conclusion gets F. • That shows that it’s possible for all the premises to be true and the conclusion false--which means the argument is invalid.

Validity • Truth tables reveal some interesting facts about how validity is related to the other notions we’ve considered. • Given certain information about premises and conclusion we can sometimes determine whether an argument is valid or invalid. • Suppose the conclusion of an argument is a tautology: does this show the argument is valid, is invalid or is this not enough information to determine whether it’s valid or invalid?

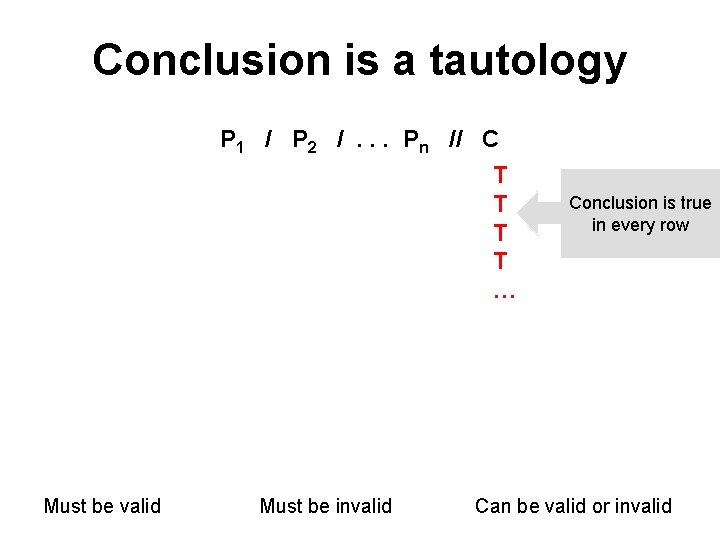
Conclusion is a tautology P 1 / P 2 /. . . Pn // C T T … Must be valid Must be invalid Conclusion is true in every row Can be valid or invalid

Conclusion is a tautology P 1 / P 2 /. . . Pn // C T T … Conclusion is true in every row There’s no row in which the conclusion is false so There’s no row in which all the premises are true and the conclusion is false so The argument must be valid. Must be valid Must be invalid Can be valid or invalid

A tautology follows from anything • We can prove a tautology from any set of premises— even if they have nothing to do with the tautology and • Even from the empty set of premises, i. e. a tautology can be proved from nothing at all! • And in doing proofs, that’s how we’ll prove a sentence is tautologous!

Premises are inconsistent P 1 / P 2 /. . . Pn // C T Must be valid T Must be invalid T There’s NO row like this Can be valid or invalid

Premises are inconsistent P 1 / P 2 /. . . Pn // C T There’s NO row like this There’s no row in which all the premises are true so There’s no row in which all the premises are true and the conclusion is false so The argument must be valid. Must be valid Must be invalid Can be valid or invalid

Ex contradictione quod libet! • Translation: From a contradiction anything follows. • If the premises are inconsistent then anything can be proved from them! • This means that if a formal system includes an inconsistency we can “prove” anything and that is BAD!

Premises + negation of conclusion inconsistent P 1 / P 2 /. . . Pn // ~ C There’s NO row like this Must be valid T T Must be invalid T T Can be valid or invalid

Premises + negation of conclusion inconsistent P 1 / P 2 /. . . Pn // ~ C There’s NO row like this T T F There’s no row in which all the premises and the negation of the conclusion are all true so There’s no row in which all the premises are true and the conclusion itself is false (by definition of negation!) so The argument must be valid. Must be valid Must be invalid Can be valid or invalid

Reducio ad Absurdem • In reducio arguments (a. k. a indirect proof, proof by contradiction) we exploit the fact that from inconsistent premises anything follows—including a contradiction. • We show that the premises + negation of conclusion of an argument are inconsistent by deriving a contradiction from them • And hence that the argument is valid!

The Problem with Truth Tables • The problem with standard truth tables is that they grow exponentially as the number of sentence letters increases, so… • Most of our work is wasted because most of the Ts and Fs we plug in don’t show anything! • Testing for consistency, for example, only the presence or absence of an all T row is relevant!

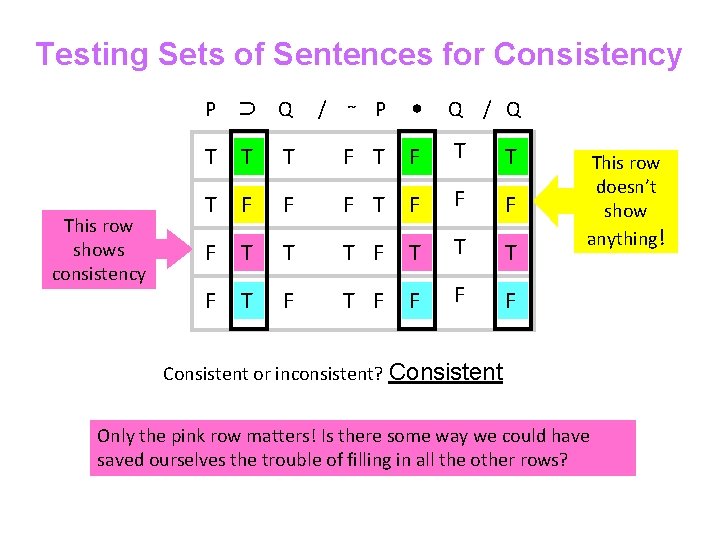
Testing Sets of Sentences for Consistency P ⊃ Q This row shows consistency / ∼ P • Q / Q T T T F F F F T T T F T F F This row doesn’t show anything! Consistent or inconsistent? Consistent Only the pink row matters! Is there some way we could have saved ourselves the trouble of filling in all the other rows?

What we need • To short-cut the truth table test for consistency we need a procedure that will do two things: – Construct a truth value assignment in which all sentences are true, if there is one and – Show conclusively that there is no truth value assignment that makes all sentences true if there isn’t one • Short-cut truth tables (Hurley 6. 5) do both these jobs. • Truth trees do them better!

Short-cut Truth Tables • Short-cut truth tables provide a quick and dirty way of testing for consistency and validity. • Instead of assigning truth values to sentence letters and calculating the truth value of whole sentences from there • We assign truth values to whole sentences and attempt to construct a truth value assignment that will produce that result. Short-cut truth tables are assbackwards

Short-Cut Truth Tables: Consistency • A set of sentences is consistent if there is some truth value assignment that makes all the sentences true • To test for consistency we write the sentences on a single line with slashes between them • We assign true to each of the sentences by writing ‘T’ under its main connective • And attempt to construct a truth value assignment that gets that result – If that’s possible, the set of sentences is consistent – If it’s not possible, the set of sentences is inconsistent

Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A T T Write the sentences on one line with slashes between them Assign true to each sentence by writing ‘T’ under its main connective

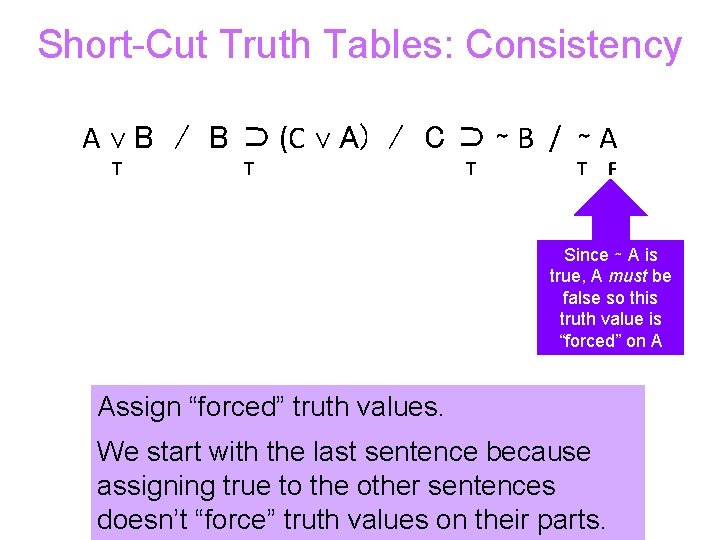
Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A T T F Since ∼ A is true, A must be false so this truth value is “forced” on A Assign “forced” truth values. We start with the last sentence because assigning true to the other sentences doesn’t “force” truth values on their parts.

Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A F T T F Now that we’ve assigned a truth value to A, other truth values are forced by that: All the other A’s must be false too!

Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A F T T T F This forces more truth values: Since A is false, to make the first sentence true we have to assign true to B—which makes all the B’s true.

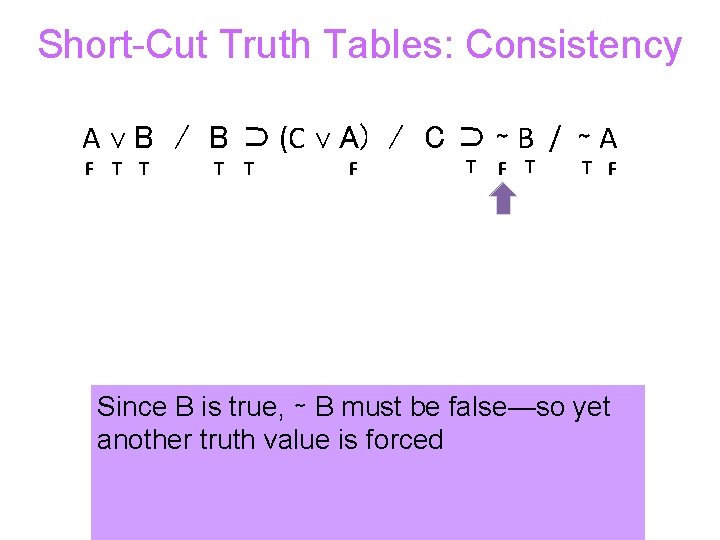
Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A F T T F Since B is true, ∼ B must be false—so yet another truth value is forced

Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A F T T F F F T T F Since B is false, C must be false in order to make the conditional, C B, true--so we have another forced truth value: all C’s have to be false

Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A F T T F F T F T T F Now we can complete the truth value assignment—and there’s only one way to do it: by assigning false to C A, since both of its parts are false.

Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A F T T F F T F T T F But this isn’t a possible truth value assignment because it says that the conditional, B (C A), is true even though its antecedent is true and its consequent false. And there’s no way to avoid this since all truth values were forced!

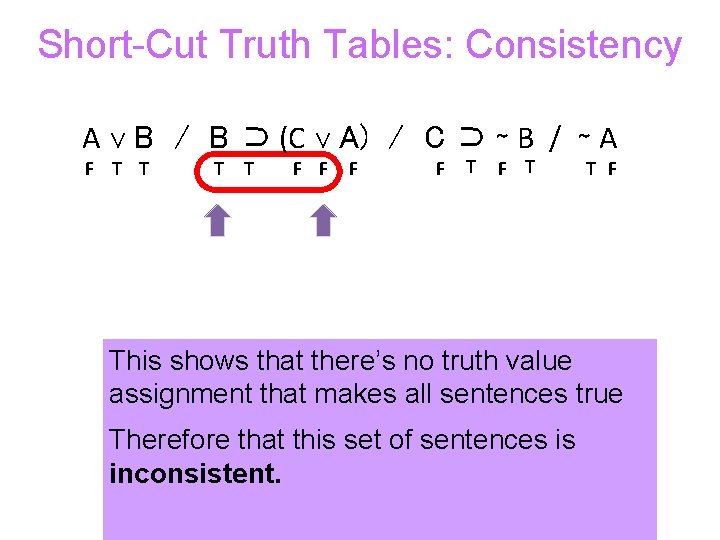
Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A F T T F F T F This shows that there’s no truth value assignment that makes all sentences true Therefore that this set of sentences is inconsistent.

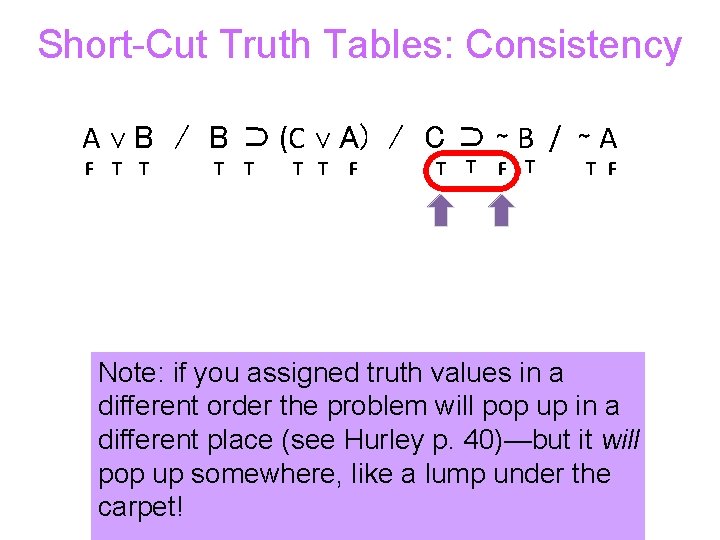
Short-Cut Truth Tables: Consistency A ∨ B / B ⊃ (C ∨ A) / C ⊃ ∼ B / ∼ A F T T T F Note: if you assigned truth values in a different order the problem will pop up in a different place (see Hurley p. 40)—but it will pop up somewhere, like a lump under the carpet!

Short-Cut Truth Tables: Validity • An argument is valid if there is no truth value assignment that makes all its premises true and its conclusion false. • To test for validity we write the argument on a single line with slashes between the premises and a double slash between the last premise and the conclusion • We assign true to each of the premises by writing ‘T’ under its main connective, and false to the conclusion by writing ‘F’ under its main connective • And attempt to construct a truth value assignment that gets that result – If that’s possible, the argument is invalid – If it’s not possible, the argument is valid

Short-Cut Truth Tables: Validity ∼A ⊃ (B T ∨ C) / ∼ B // C ⊃ A T F We assign true to each of the premises by writing ‘T’ under its main connective and assign false to the conclusion by writing ‘F’ under it’s main connective. We’re seeing if we can show invalidity.

Short-Cut Truth Tables: Validity ∼A ⊃ (B T ∨ C) / ∼ B // C ⊃ A T T F F Making the conclusion, C A, false forces C to be true and A to be false since that’s the only case in which a conditional is false.

Short-Cut Truth Tables: Validity ∼A ⊃ (B F T ∨ C) / ∼ B // C ⊃ A T T T F F This forces truth values on all the other C’s and A’s: all the C’s get true and the A’s get false

Short-Cut Truth Tables: Validity ∼A ⊃ (B T F ∨ C) / ∼ B // C ⊃ A T T F F There are more forced truth values: since ∼B is true, B must be false, so we assign ‘F’ to all the B’s And now that we know A is false, ∼A must be true.

Short-Cut Truth Tables: Validity ∼A ⊃ (B T F T C) / ∼ B // C ⊃ A ∨ F T T T F F Now we can complete the table by filling in the truth value for the first premise. So the first premise is a true conditional with a true antecedent and true consequent—and that’s ok. The other sentences are ok too.

Short-Cut Truth Tables: Validity ∼A ⊃ (B T F T C) / ∼ B // C ⊃ A ∨ F T T T F F Since everything’s ok, this is a possible truth value assignment Since this truth value assignment makes all the premises true and the conclusion false the argument is shown to be invalid.