True bearings LO Use trigonometric ratios to solve

True bearings LO: Use trigonometric ratios to solve problems involving bearings www. mathssupport. org

Compass points 45° between north and west N NW E W SW 45° between south and west www. mathssupport. org 45° between North and east NE S SE 45° between south and east

Compass points When using Compass points for direction, you will see notation such as. N 35° E N Which means 35° east of North 35° E W www. mathssupport. org S

Compass points When using Compass points for direction, you will see notation such as. W 25° S N Which means 25° south of west W E 25° W 25° S www. mathssupport. org S

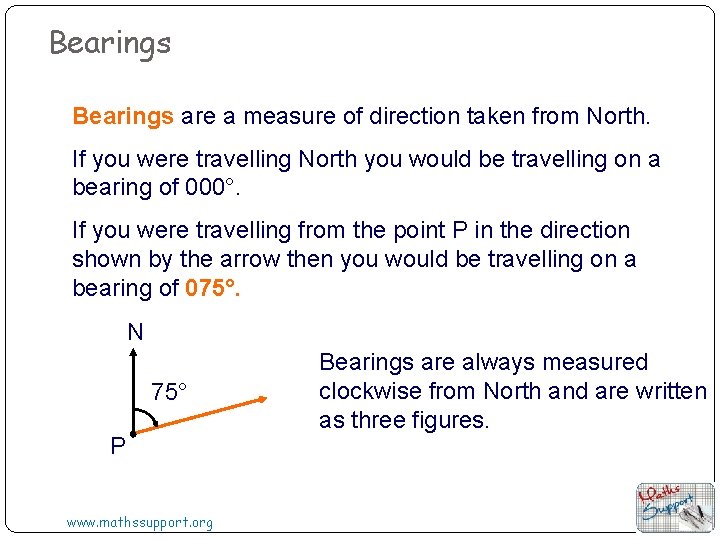
Bearings are a measure of direction taken from North. If you were travelling North you would be travelling on a bearing of 000°. If you were travelling from the point P in the direction shown by the arrow then you would be travelling on a bearing of 075°. 000°. N 75° P www. mathssupport. org Bearings are always measured clockwise from North and are written as three figures.

Bearings The bearing from point A to point B is 105º. What is the bearing from point B to point A? N The angle from B to A is N A 105º + 180º = 285º 105º ? 105º B 180° www. mathssupport. org This is called a back bearing.

Bearings An airplane departs from A and flies on a 138 o course for 342 km. It then changes direction to a 228 o course and flies a further 482 km to town C. (a) Find the distance of C from A. (b) Find the bearing of C from A. 48 2 k m Sketch a fully labelled diagram N With this information we can calculate the 138º angle ABC A The airplane turns 228º – 138º = 90º 34 2 k N ∴ angle ABC = 90º m B 591 km We use Pythagoras theorem to Find AC 228º AC 2 = AB 2 + BC 2 Cwww. mathssupport. org = 3422 + 4822 AC = 591 km

Bearings An airplane departs from A and flies on a 138 o course for 342 km. It then changes direction to a 228 o course and flies a further 485 km to town C. (a) Find the distance of C from A. (b) Find the bearing of C from A. Sketch a diagram N 138º A 48 5 k m To find the bearing of C from A we need the angle measured from the north to the line AC. 34 To find this angle we need the angle BAC 2 k q m N named q B 485 -1 591 km tan = q Find q 342 228º q ≈ 54. 8 o The required angle is 138 + 54. 8 ≈ 192. 8 Cwww. mathssupport. org The bearing of C from A is about 192. 8.

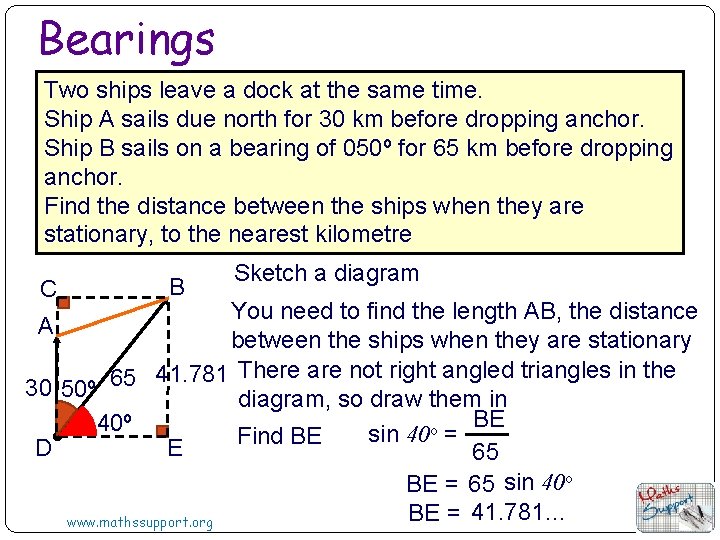
Bearings Two ships leave a dock at the same time. Ship A sails due north for 30 km before dropping anchor. Ship B sails on a bearing of 050º for 65 km before dropping anchor. Find the distance between the ships when they are stationary, to the nearest kilometre C B Sketch a diagram You need to find the length AB, the distance A between the ships when they are stationary 41. 781 There are not right angled triangles in the 65 30 50º diagram, so draw them in BE 40º o sin 40 = Find BE D E 65 BE = 65 sin 40 o BE = 41. 781… www. mathssupport. org

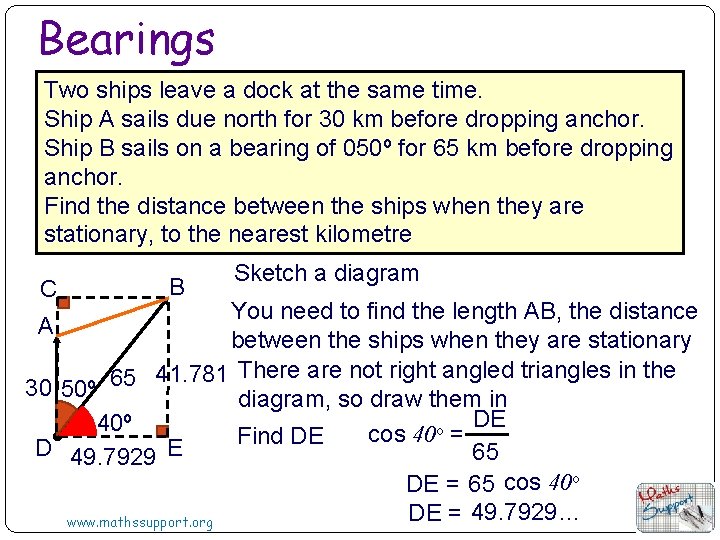
Bearings Two ships leave a dock at the same time. Ship A sails due north for 30 km before dropping anchor. Ship B sails on a bearing of 050º for 65 km before dropping anchor. Find the distance between the ships when they are stationary, to the nearest kilometre C B Sketch a diagram You need to find the length AB, the distance A between the ships when they are stationary 41. 781 There are not right angled triangles in the 65 30 50º diagram, so draw them in DE 40º o cos 40 = Find DE D 49. 7929 E 65 DE = 65 cos 40 o DE = 49. 7929… www. mathssupport. org

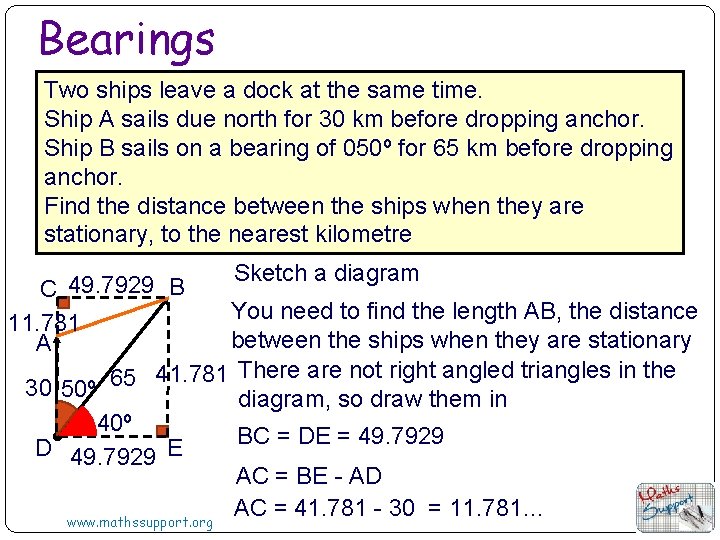
Bearings Two ships leave a dock at the same time. Ship A sails due north for 30 km before dropping anchor. Ship B sails on a bearing of 050º for 65 km before dropping anchor. Find the distance between the ships when they are stationary, to the nearest kilometre Sketch a diagram 49. 7929 B C You need to find the length AB, the distance 11. 781 between the ships when they are stationary A 41. 781 There are not right angled triangles in the 65 30 50º diagram, so draw them in 40º BC = DE = 49. 7929 D 49. 7929 E AC = BE - AD AC = 41. 781 - 30 = 11. 781… www. mathssupport. org

Bearings Two ships leave a dock at the same time. Ship A sails due north for 30 km before dropping anchor. Ship B sails on a bearing of 050º for 65 km before dropping anchor. Find the distance between the ships when they are stationary, to the nearest kilometre Sketch a diagram 49. 7929 B C You need to find the length AB, the distance 11. 781 between the ships when they are stationary A 41. 781 There are not right angled triangles in the 65 30 50º diagram, so draw them in 40º AB 2 = (49. 7929…)2 + (11. 7812…)2 D 49. 7929 E AB = 51. 1677 The ships are approximately 51 km apart www. mathssupport. org

Thank you for using resources from For more resources visit our website https: //www. mathssupport. org If you have a special request, drop us an email info@mathssupport. org www. mathssupport. org