TrigonometryThe study of the properties of triangles Trigonometry

• Trigonometry--The study of the properties of triangles. Trigonometry means angle measurement. • Trigonometric Ratio--The ratios of the measures of two sides of a right triangle.

Find Sine, Cosine, and Tangent Ratios A. Express sin L as a fraction and as a decimal to the nearest hundredth. Answer:

Find Sine, Cosine, and Tangent Ratios B. Express cos L as a fraction and as a decimal to the nearest hundredth. Answer:

Find Sine, Cosine, and Tangent Ratios C. Express tan L as a fraction and as a decimal to the nearest hundredth. Answer:

Find Sine, Cosine, and Tangent Ratios D. Express sin N as a fraction and as a decimal to the nearest hundredth. Answer:

Find Sine, Cosine, and Tangent Ratios E. Express cos N as a fraction and as a decimal to the nearest hundredth. Answer:

Find Sine, Cosine, and Tangent Ratios F. Express tan N as a fraction and as a decimal to the nearest hundredth. Answer:

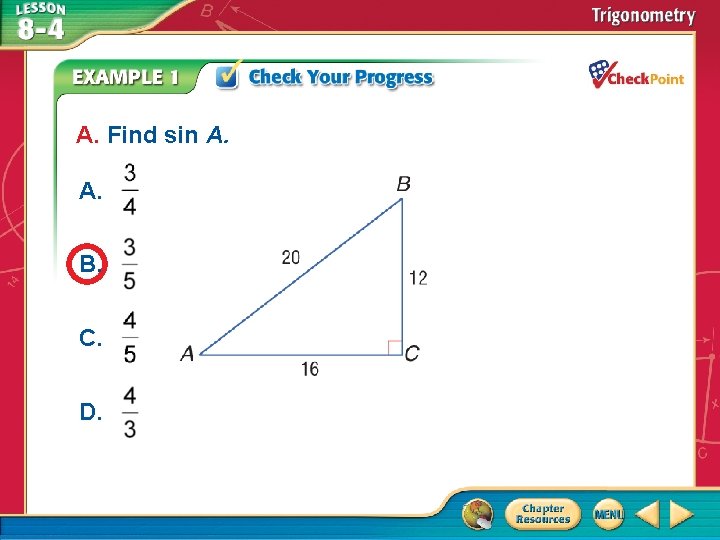
A. Find sin A. A. B. C. D. A B C D

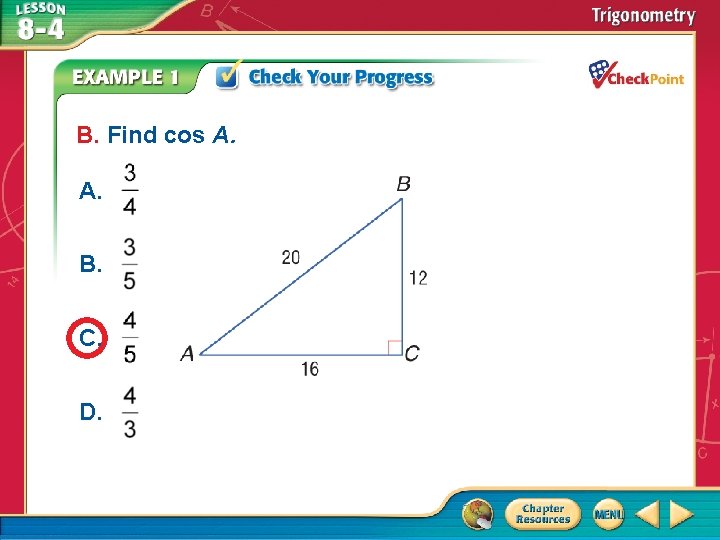
B. Find cos A. A. B. C. D. A B C D

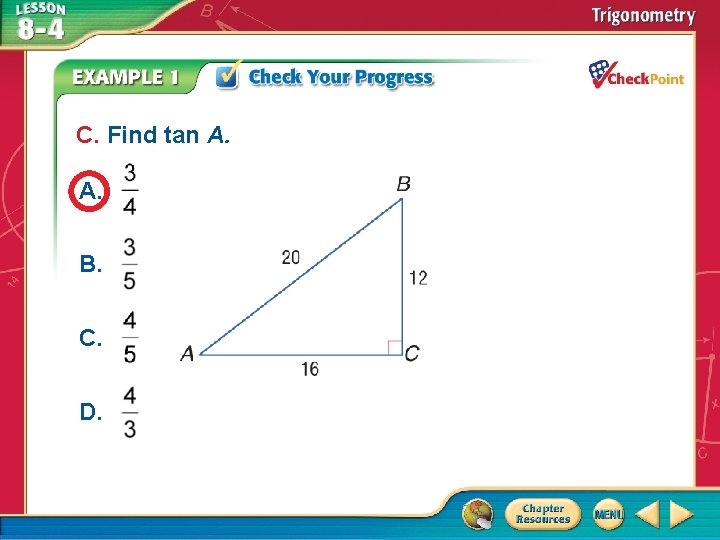
C. Find tan A. A. B. C. D. A B C D

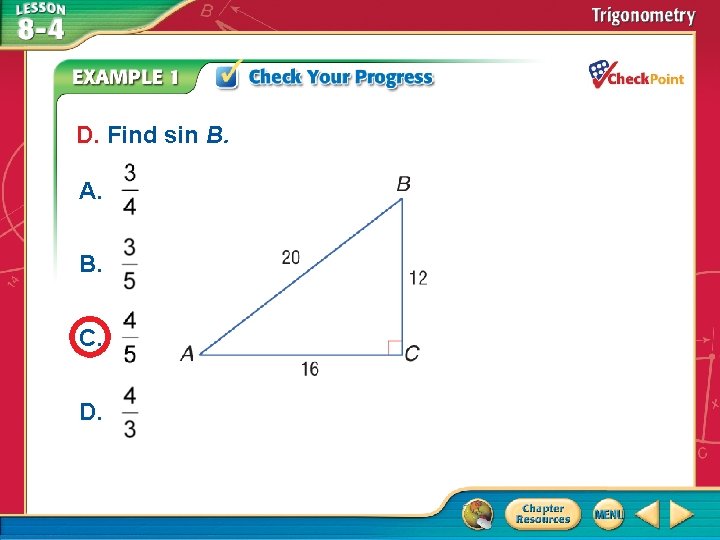
D. Find sin B. A. B. C. D. A B C D

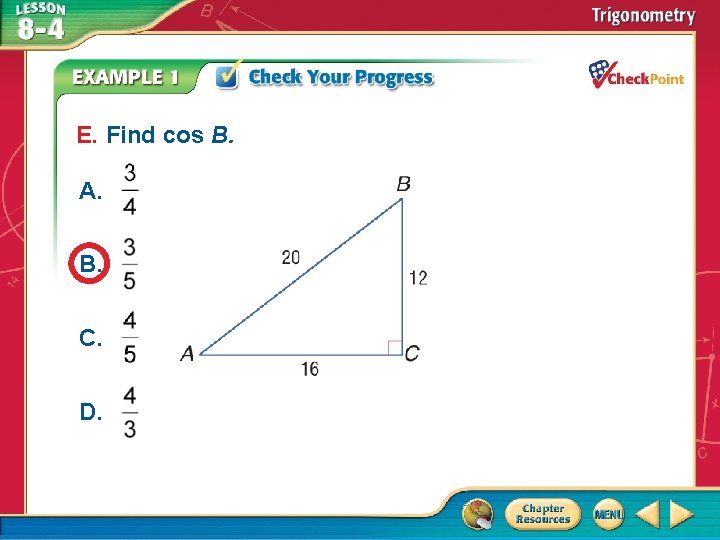
E. Find cos B. A. B. C. D. A B C D

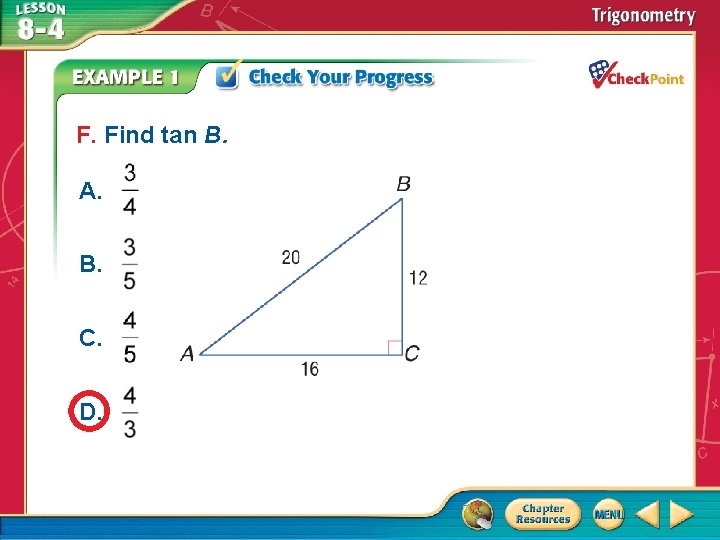
F. Find tan B. A. B. C. D. A B C D

Use Special Right Triangles to Find Trigonometric Ratios Use a special right triangle to express the cosine of 60° as a fraction and as a decimal to the nearest hundredth. Draw and label the side lengths of a 30°-60°-90° right triangle, with x as the length of the shorter leg and 2 x as the length of the hypotenuse. The side adjacent to the 60° angle has a measure of x.

Use Special Right Triangles to Find Trigonometric Ratios Definition of cosine ratio Substitution Simplify.

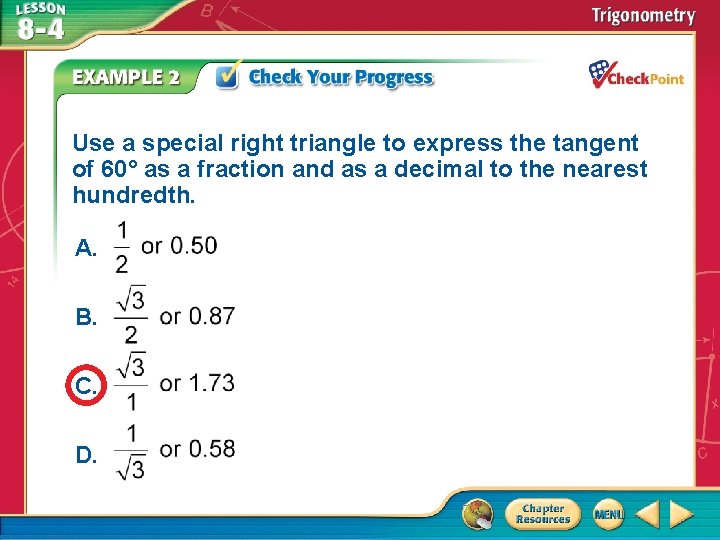
Use a special right triangle to express the tangent of 60° as a fraction and as a decimal to the nearest hundredth. A. B. C. D. A B C D

Estimate Measures Using Trigonometry EXERCISING A fitness trainer sets the incline on a treadmill to 7°. The walking surface is 5 feet long. Approximately how many inches did the trainer raise the end of the treadmill from the floor? Let y be the height of the treadmill from the floor in inches. The length of the treadmill is 5 feet, or 60 inches.

Estimate Measures Using Trigonometry Multiply each side by 60. Use a calculator to find y. KEYSTROKES: 60 SIN 7 ENTER 7. 312160604 Answer: The treadmill is about 7. 3 inches high.

CONSTRUCTION The bottom of a handicap ramp is 15 feet from the entrance of a building. If the angle of the ramp is about 4. 8°, about how high does the ramp rise off the ground to the nearest inch? A. 1 in. B. 11 in. C. 16 in. D. 15 in. A. B. C. D. A B C D

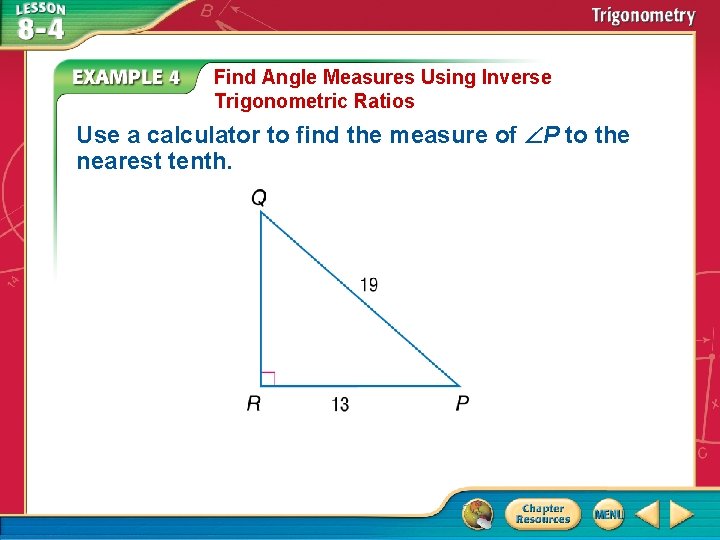
Find Angle Measures Using Inverse Trigonometric Ratios Use a calculator to find the measure of P to the nearest tenth.

Find Angle Measures Using Inverse Trigonometric Ratios The measures given are those of the leg adjacent to P and the hypotenuse, so write the equation using the cosine ratio. KEYSTROKES: 2 nd [COS] ( 13 ÷ 19 ) ENTER 46. 82644889 Answer: So, the measure of P is approximately 46. 8°.

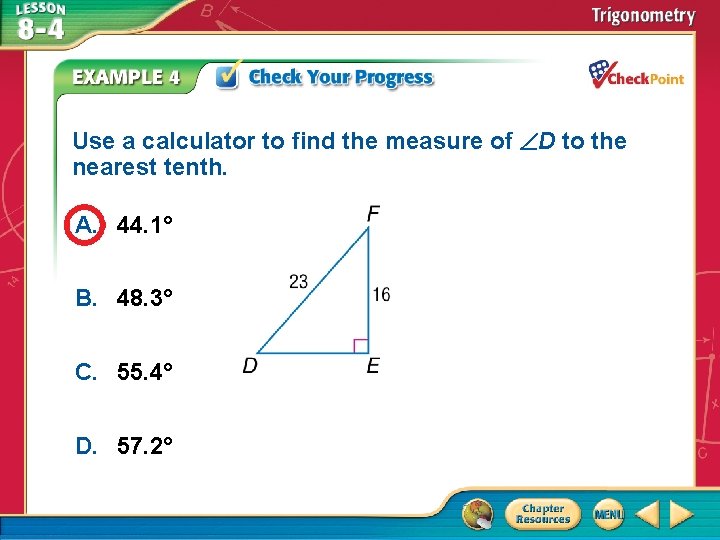
Use a calculator to find the measure of D to the nearest tenth. A. 44. 1° B. 48. 3° C. 55. 4° D. 57. 2° A. B. C. D. A B C D

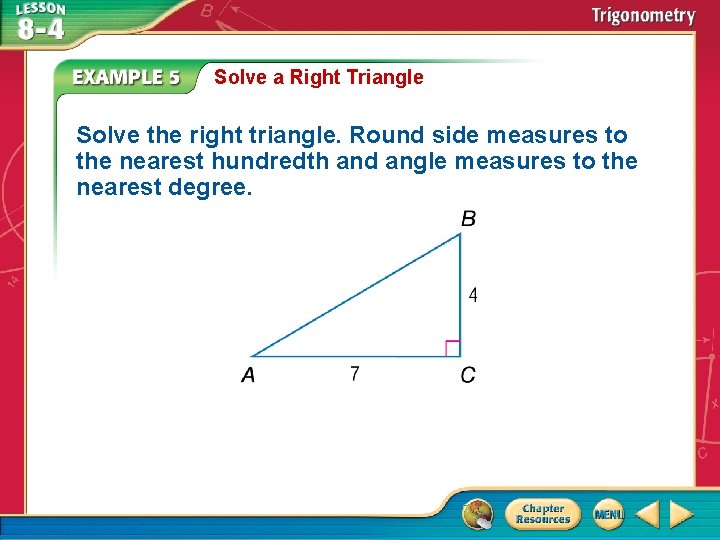
Solve a Right Triangle Solve the right triangle. Round side measures to the nearest hundredth and angle measures to the nearest degree.

Solve a Right Triangle Step 1 Find m A by using a tangent ratio. Definition of inverse tangent 29. 7448813 ≈ m A Use a calculator. So, the measure of A is about 30.

Solve a Right Triangle Step 2 Find m B using complementary angles. m A + m B = 90 Definition of complementary angles 30 + m B ≈ 90 m B ≈ 60 Subtract 30 from each side. So, the measure of B is about 60. m A ≈ 30

Solve a Right Triangle Step 3 Theorem Find AB by using the Pythagorean Theorem. (AC)2 + (BC)2= (AB)2 Pythagorean 72 + 4 2 = (AB)2 Substitution 65 (AB)2 Simplify. = Take the positive square root of each side. 8. 06 ≈ AB Use a calculator.

Solve a Right Triangle So, the measure of AB is about 8. 06. Answer: m A ≈ 30, m B ≈ 60, AB ≈ 8. 06

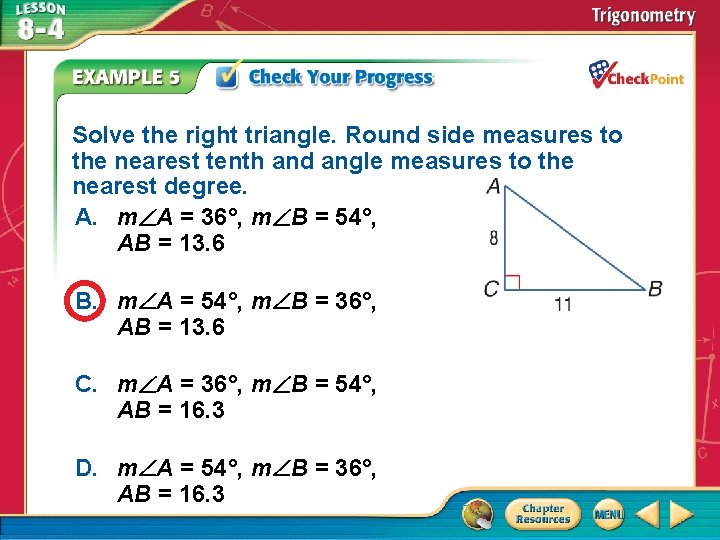
Solve the right triangle. Round side measures to the nearest tenth and angle measures to the nearest degree. A. m A = 36°, m B = 54°, AB = 13. 6 B. m A = 54°, m B = 36°, AB = 13. 6 C. m A = 36°, m B = 54°, AB = 16. 3 D. m A = 54°, m B = 36°, AB = 16. 3 A. B. C. D. A B C D

• Summary: – If you are given the angle, use sin, cos, and tan – If you want to find the angle, use sin-1, cos-1, and tan-1