Trigonometry small angle approximations KUS objectives BAT derive

Trigonometry: small angle approximations • KUS objectives BAT derive and use the small angle approximations for sin x, cos x and tan x Starter: Complete these ‘adjusted’ Identities

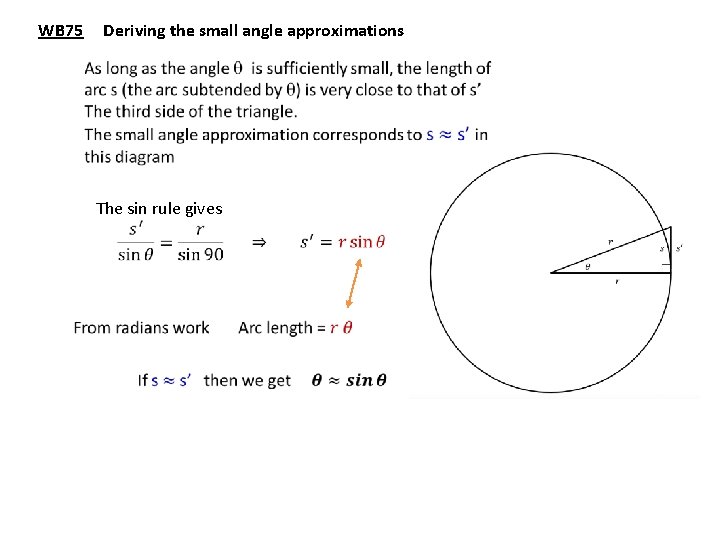
WB 75 Deriving the small angle approximations The sin rule gives

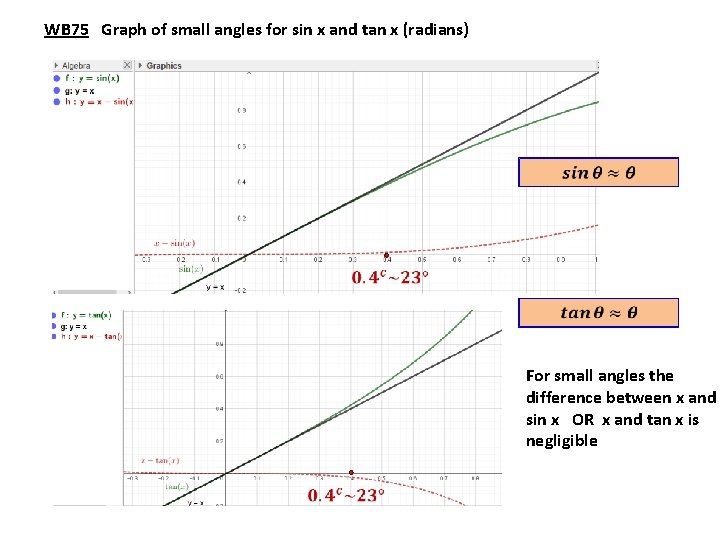
WB 75 Graph of small angles for sin x and tan x (radians) For small angles the difference between x and sin x OR x and tan x is negligible

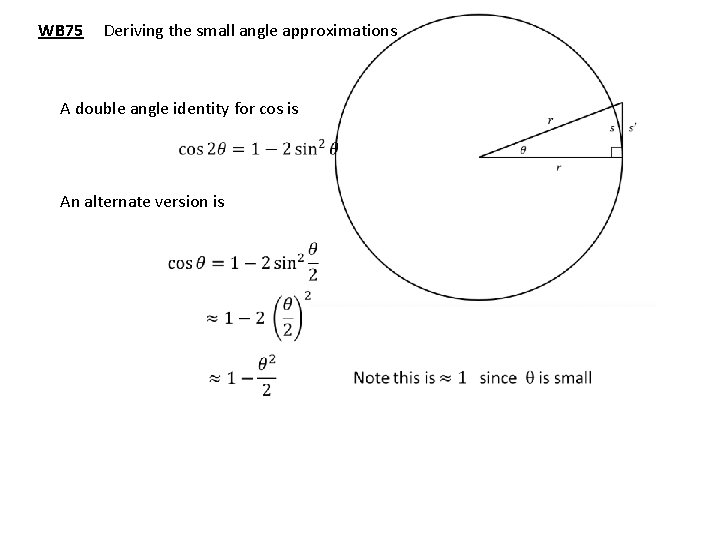
WB 75 Deriving the small angle approximations A double angle identity for cos is An alternate version is

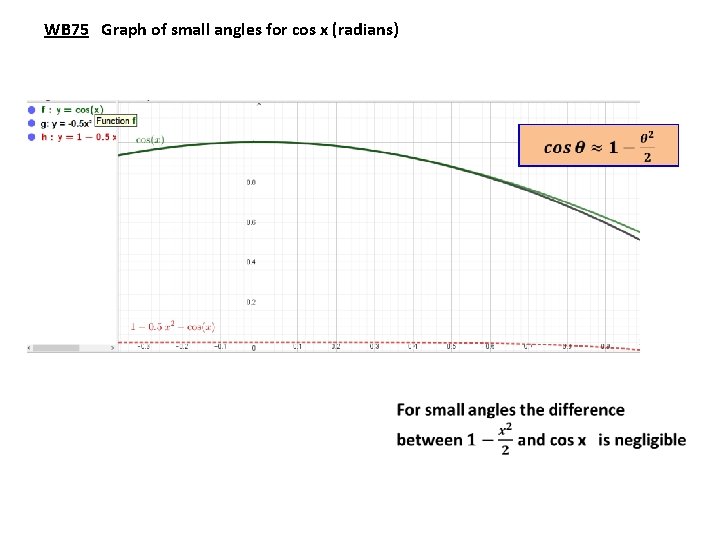
WB 75 Graph of small angles for cos x (radians)

WB 75 Summary small angle approximations In the formula booklet you are given “The small-angle approximation is used ubiquitously throughout fields of physics including mechanics, waves and optics, electromagnetism, astronomy, …” look it up on Wickipedia for more The main application of this in A level is with proof from first principles of the derivatives of sin x and cos x.

WB 76 Find a approximation to each of the following and compare / evaluate your answers to with those given by your calculator Calculator Pretty close!

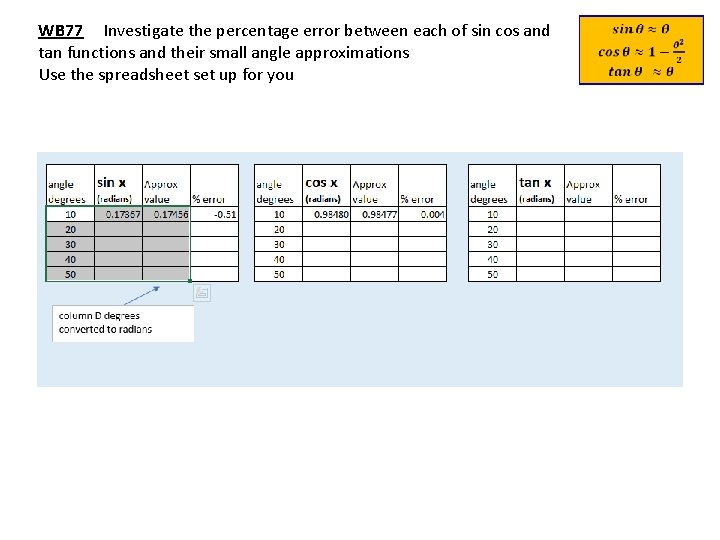
WB 77 Investigate the percentage error between each of sin cos and tan functions and their small angle approximations Use the spreadsheet set up for you

Using trig identity

Is there another way to start the question?

If we try and simplify the expression in Trig terms first Now use the approximations

• KUS objectives BAT derive and use the small angle approximations for sin x, cos x and tan x self-assess using: R / A / G ‘I am now able to ____. To improve I need to be able to ____’