Trigonometry Review Part 5 Identities and Solving Equations

Trigonometry Review (Part 5) – Identities and Solving Equations The presentation will review the following: • Trigonometric Identities • Solving Trigonometric Equations

Trigonometry Review – Part 5 The trigonometric identities are used to manipulate trigonometric expressions into convenient forms for solving, factoring, reducing etc. There are three main sets of identities that are used often in calculus: • • • Reciprocal Identities Quotient Identities Pythagorean Identities There are some others that we will see, but not very often.

Trigonometry Review – Part 5 We have already seen and used reciprocal and quotient identities. They are as follows: Reciprocal Identities Quotient Identities

Trigonometry Review – Part 5 The Pythagorean Identities always involve the squares of trigonometric functions. The most important (and easiest) Pythagorean Identity to remember is: As a matter of fact, this is the only Pythagorean Identity that I memorize. You are welcome to memorize all three, but the other two can be derived from this one.

Trigonometry Review – Part 5 If we start with this one Pythagorean Identity, we can derive the other two by: Dividing both sides of the equation by sin 2Ө: Dividing both sides of the equation by cos 2Ө: Split the addition Use reciprocal and quotient identities to simplify

Trigonometry Review – Part 5 The three Pythagorean Identities are as follows: (You may need to use each of these in different forms) Memorization is not really an option here. Remember, all of this can be derived by manipulating the first identity.

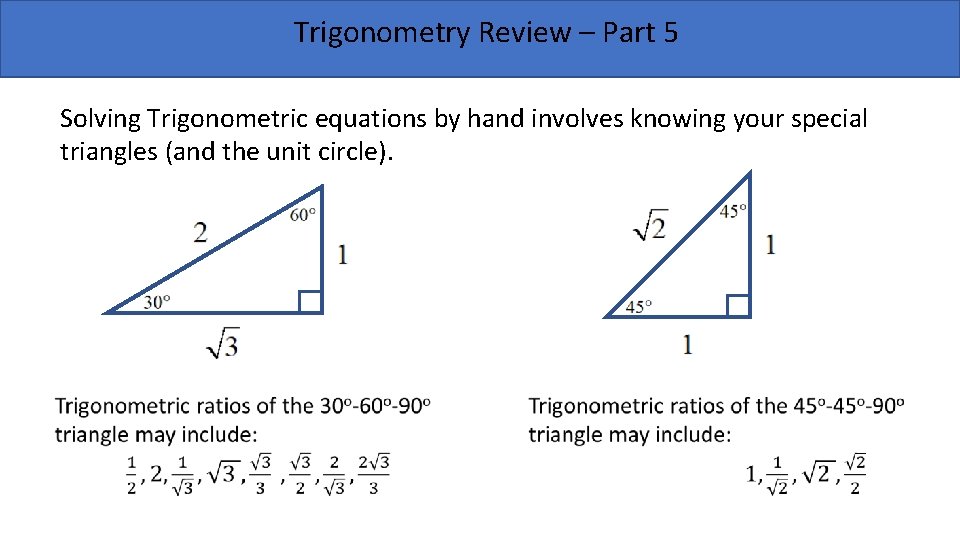
Trigonometry Review – Part 5 Solving Trigonometric equations by hand involves knowing your special triangles (and the unit circle).

Trigonometry Review – Part 5 Opp. Adj.

Trigonometry Review – Part 5 Opp. Adj. or using radians Solving the equation(s)

Trigonometry Review – Part 5

Trigonometry Review – Part 5 Solving the equation using radians: 45 o or

Trigonometry Review – Part 5 Subtract from both sides factor split This equation has 5 solutions.