trigonometry Radian measure Sin cos and tan of

trigonometry • Radian measure • Sin cos and tan of angles measured in radians

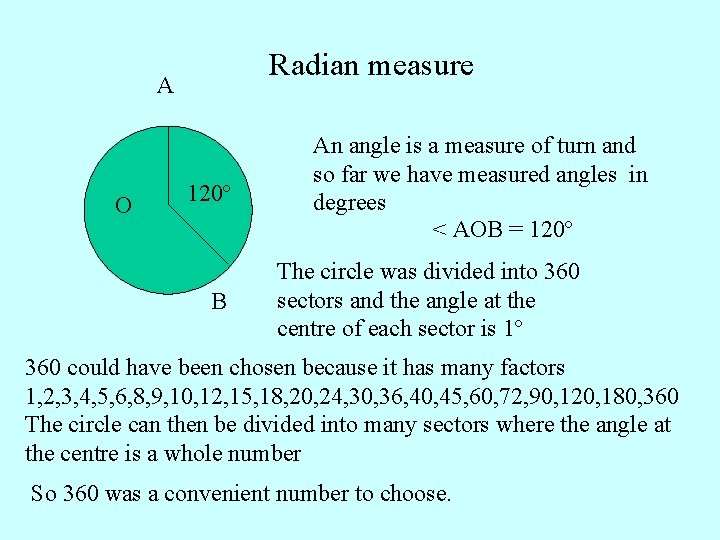
Radian measure A O 120º B An angle is a measure of turn and so far we have measured angles in degrees < AOB = 120º The circle was divided into 360 sectors and the angle at the centre of each sector is 1º 360 could have been chosen because it has many factors 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360 The circle can then be divided into many sectors where the angle at the centre is a whole number So 360 was a convenient number to choose.

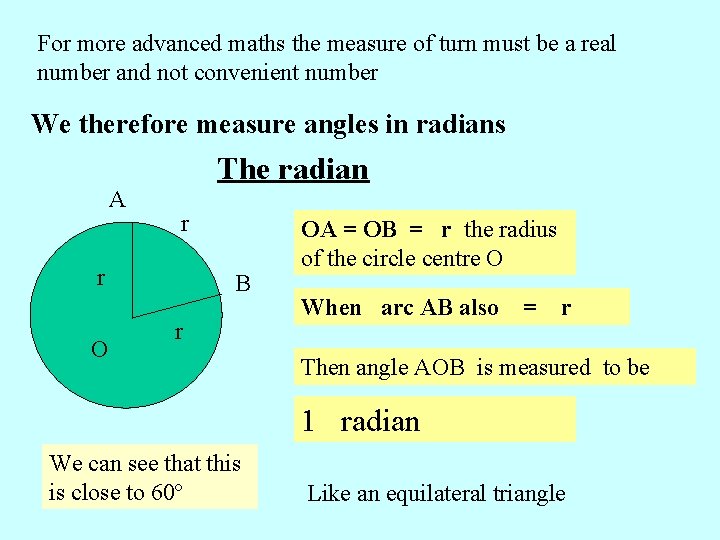
For more advanced maths the measure of turn must be a real number and not convenient number We therefore measure angles in radians A The radian r r O B r OA = OB = r the radius of the circle centre O When arc AB also = r Then angle AOB is measured to be 1 radian We can see that this is close to 60º Like an equilateral triangle

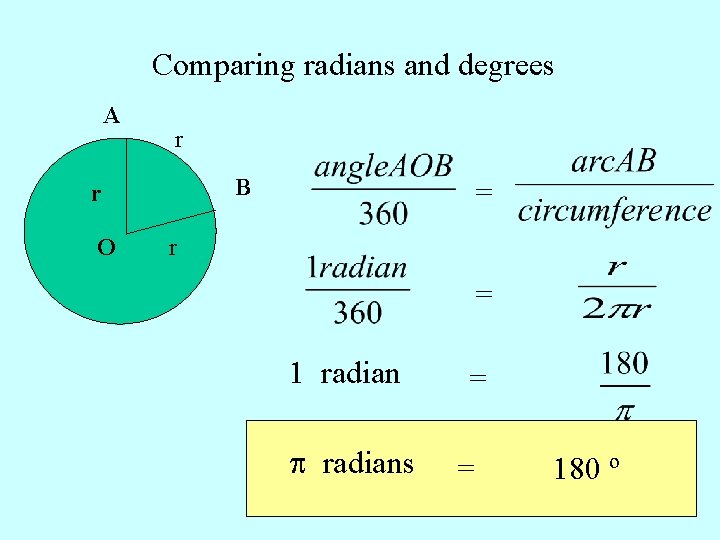
Comparing radians and degrees A r B r O = r = 1 radians = = 180 º

We should now be able to change degrees into radians using 180 º = radians 90 º = radians The fraction the angle 90 is of 180 is the same as the fraction the angle in radians is of that is 1/2 Similarly 45º = /4 60º = /3 Calculating angles 135º = 3 X 45º = 3 X /4 =3 /4 30º = /6 > 90 Express as a multiple of 30, 45 or 60 In most of our work with radians the angle is expressed as a multiple of . So we should be able to convert easily between degrees and radians or memorise them

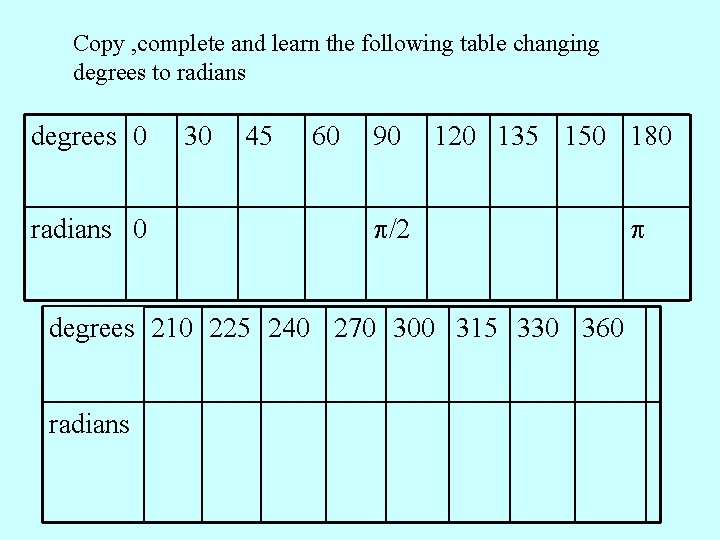
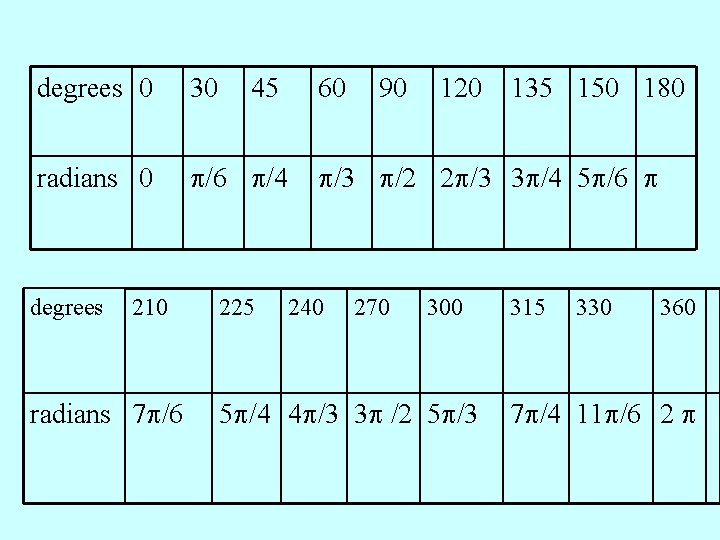
Copy , complete and learn the following table changing degrees to radians degrees 0 radians 0 30 45 60 90 120 135 150 180 /2 degrees 210 225 240 270 300 315 330 360 radians

degrees 0 30 radians 0 /6 /4 degrees 210 radians 7 /6 45 225 60 90 120 135 150 180 /3 /2 2 /3 3 /4 5 /6 240 270 300 5 /4 4 /3 3 /2 5 /3 315 330 360 7 /4 11 /6 2

Changing degrees which are not multiples of 30, 45 and 60 to radians Change 70º to radians Start with Use direct proportion Using a calculator does not give the exact value 180 º = radians This is the exact value 70º = 1. 22 radians`

Change the following angles in degrees to radians give angle as a fraction of and as a number to 3 dp degrees fraction 20 º 1/9 40 º 2/9 number 0. 349 0. 698 1. 396 80 º 4/9 140 º 7/9 2. 443 200 º 11/9 3. 840 320 º 16/9 5. 59 144 º 4/5 2. 513 280 º 14/9 4. 887

Convert radians to degrees 3 /2 = 3 X 90º = 270º 7 /6 = 7 X 30º = 210º Other radians measures Rads = 180º 6 rads = 6/ X 180 º 343. 8 º Using the calculator

Change the following radian measures to degrees 7 rads 5 /4 rads 7/ X 180 = 565º 5 X /4 = 5 X 45º 6. 28 rads 6. 28/ x 180 = 360º 14 rads 14/ x 180 7 X /12 = 802º = 7 X 15 7 /12 rads 4. 2/ X 180 = 240. 6º 1. 4 rads 1. 4/ X 180 = 97º 5 /3 rads 5 X /3 = 5 X 60 = 225º = 105º = 300º

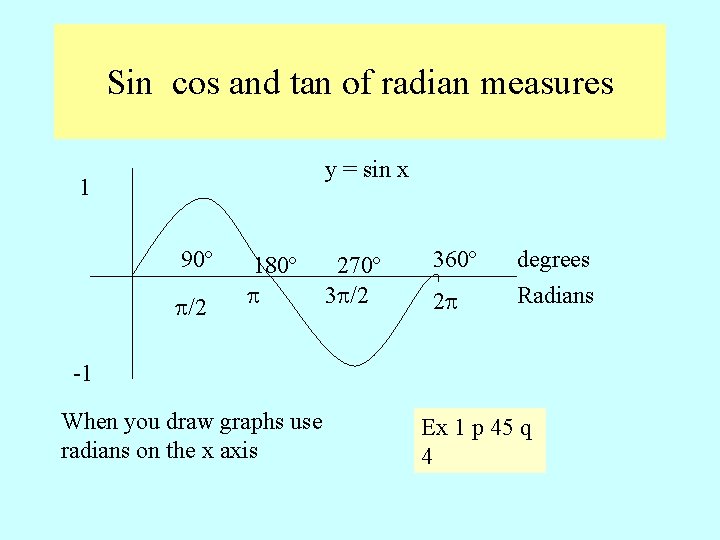
Sin cos and tan of radian measures y = sin x 1 90º /2 180º 270º 3 /2 360º 2 degrees Radians -1 When you draw graphs use radians on the x axis Ex 1 p 45 q 4

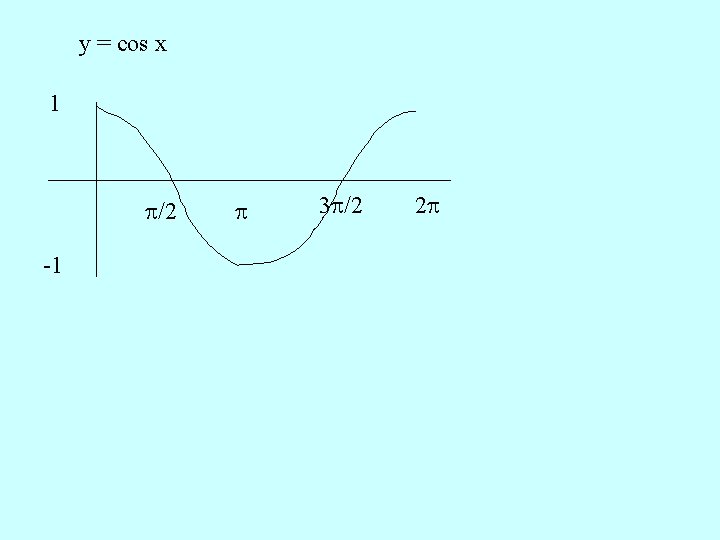
y = cos x 1 /2 -1 3 /2 2

Trigonometry 3. Exact Values Some special values of Sin, Cos and Tan are useful left as fractions, We call these exact values Consider 60º 2 60º 30º 2 2 2 3 60º To provide values for 30º and 60º 1

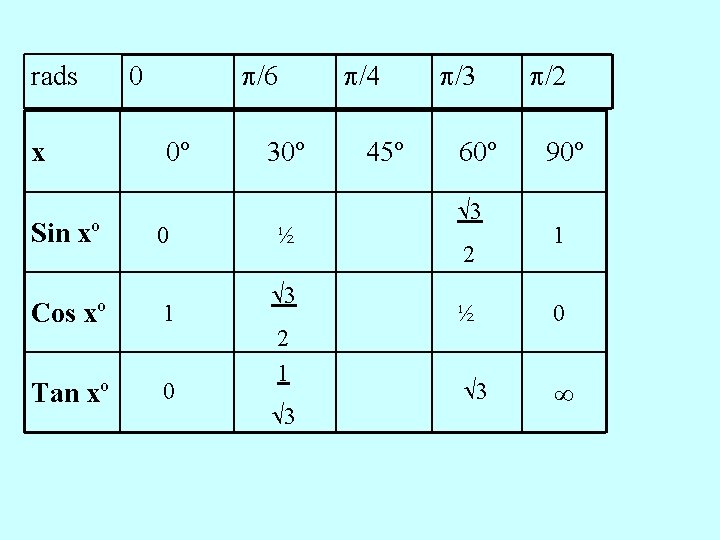
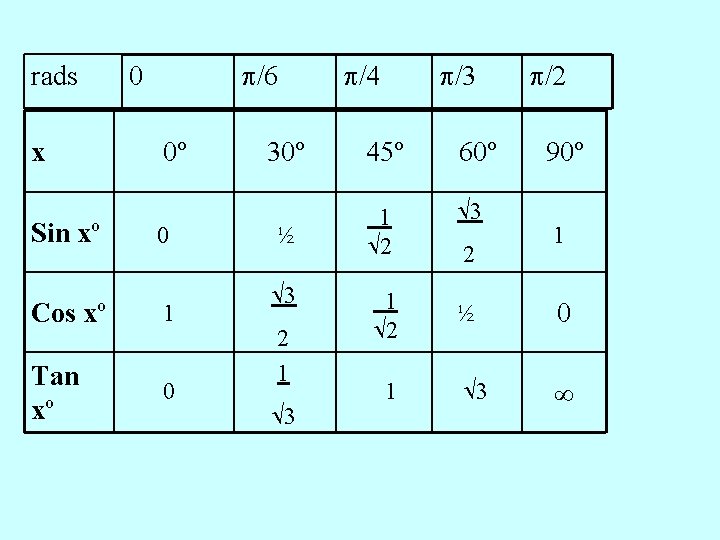
rads x Sin xº /6 0 0º 0 Cos xº 1 Tan xº 0 30º ½ 3 2 1 3 /4 45º /3 60º 3 2 /2 90º 1 ½ 0 3

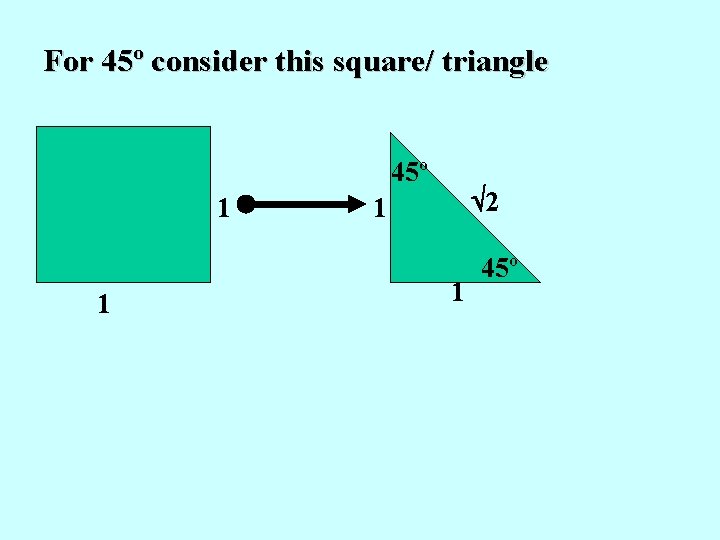
For 45º consider this square/ triangle 45º 1 1 2 1 1 45º

rads x Sin xº /6 0 0º 0 Cos xº 1 Tan xº 0 /4 /3 /2 30º 45º 60º ½ 1 2 3 1 2 ½ 0 3 3 2 1 3 1 2 90º 1

The exact value of sin /3 The exact value of cos /2 = 3/2 =0 We can also express these trig ratios to 2 decimal places using the calculator but remember to change to radian mode Cos /2 Or = cos ( /2) cos 1. 57 Ex 1 p 45 q 6, 7 8 =0 = 0