Trigonometry Graphs www mathsrevision com S 4 Credit

Trigonometry Graphs www. mathsrevision. com S 4 Credit Exact values for Sin Cos and Tan Angles greater than 90 o Graphs of the form y = a sin xo Graphs of the form y = a sin bxo Solving Trig Equations Special trig relationships created by Mr. Lafferty

Starter Questions www. mathsrevision. com S 4 Credit 03 -Dec-20 Created by Mr Lafferty Maths Dept

Exact Values www. mathsrevision. com S 4 Credit Learning Intention 1. To build on basic trigonometry values. Success Criteria 1. Recognise basic triangles and exact values for sin, cos and tan 30 o, 45 o, 60 o. 2. Calculate exact values for problems. 03 -Dec-20 Created by Mr Lafferty Maths Dept

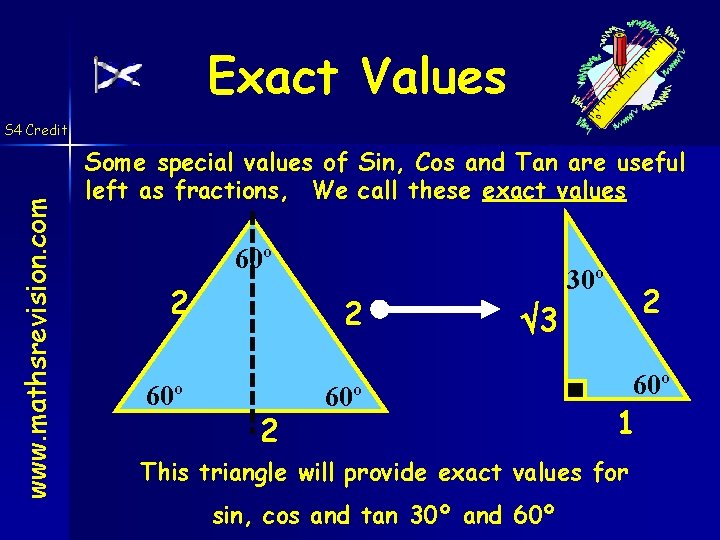
Exact Values www. mathsrevision. com S 4 Credit Some special values of Sin, Cos and Tan are useful left as fractions, We call these exact values 60º 2 2 60º 2 30º 2 3 1 This triangle will provide exact values for sin, cos and tan 30º and 60º

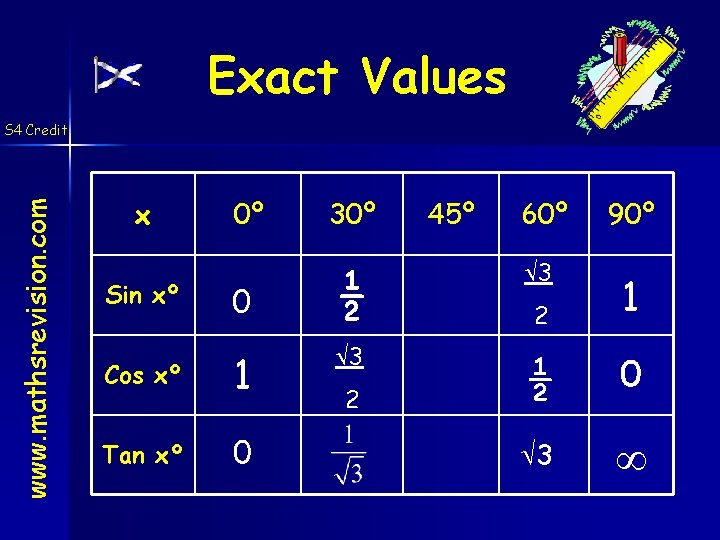
Exact Values www. mathsrevision. com S 4 Credit x Sin xº 0º 0 Cos xº 1 Tan xº 0 30º 60º 90º ½ 3 2 1 3 ½ 0 3 2 45º

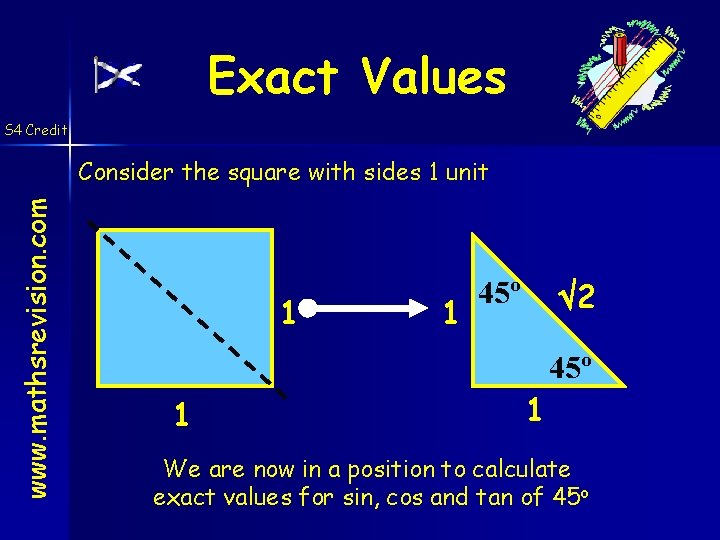
Exact Values S 4 Credit www. mathsrevision. com Consider the square with sides 1 unit 1 1 45º 2 45º 1 1 We are now in a position to calculate exact values for sin, cos and tan of 45 o

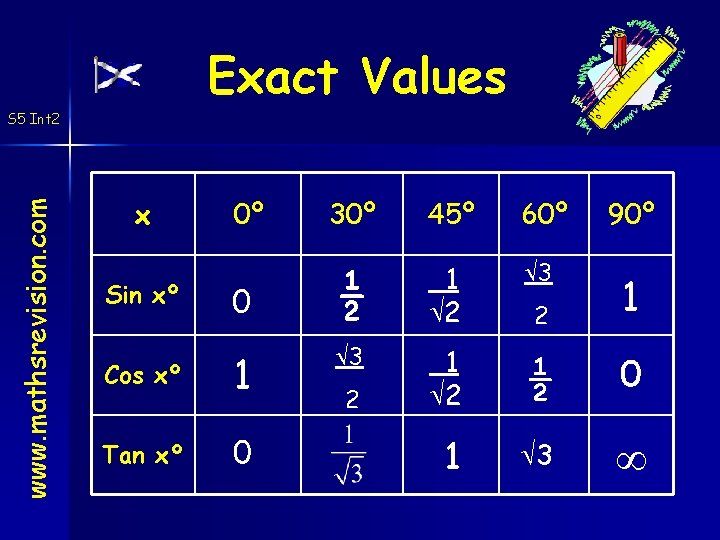
Exact Values www. mathsrevision. com S 5 Int 2 x Sin xº 0º 0 Cos xº 1 Tan xº 0 30º 45º 60º 90º ½ 1 2 3 2 1 3 1 2 ½ 0 1 3 2

Exact Values www. mathsrevision. com S 5 Int 2 Now try Ex 2. 1 Ch 11 (page 220) 03 -Dec-20 Created by Mr Lafferty Maths Dept

Starter Questions www. mathsrevision. com S 4 credit 03 -Dec-20 Created by Mr Lafferty Maths Dept

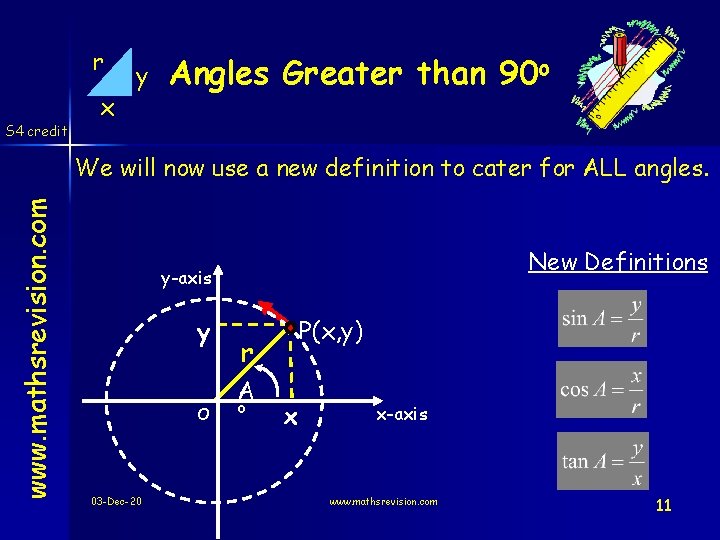
Angles Greater than 90 o www. mathsrevision. com S 4 credit Learning Intention 1. Introduce definition of sine, cosine and tangent over 360 o using triangles with the unity circle. 03 -Dec-20 Success Criteria 1. Find values of sine, cosine and tangent over the range 0 o to 360 o. 2. Recognise the symmetry and equal values for sine, cosine and tangent. Created by Mr. Lafferty Maths Dept.

r S 4 credit x y Angles Greater than 90 o www. mathsrevision. com We will now use a new definition to cater for ALL angles. New Definitions y-axis y O 03 -Dec-20 P(x, y) r A o x x-axis www. mathsrevision. com 11

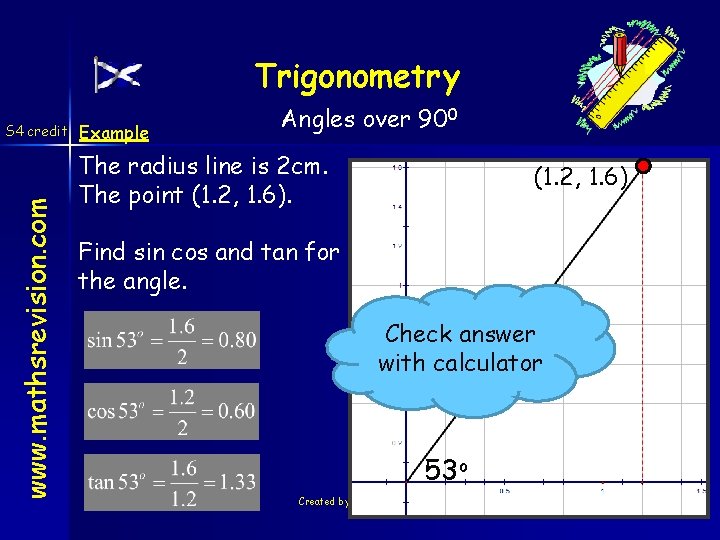
Trigonometry www. mathsrevision. com S 4 credit Example Angles over 900 The radius line is 2 cm. The point (1. 2, 1. 6) Find sin cos and tan for the angle. Check answer with calculator 53 o 03 -Dec-20 Created by Mr Lafferty Maths Dept

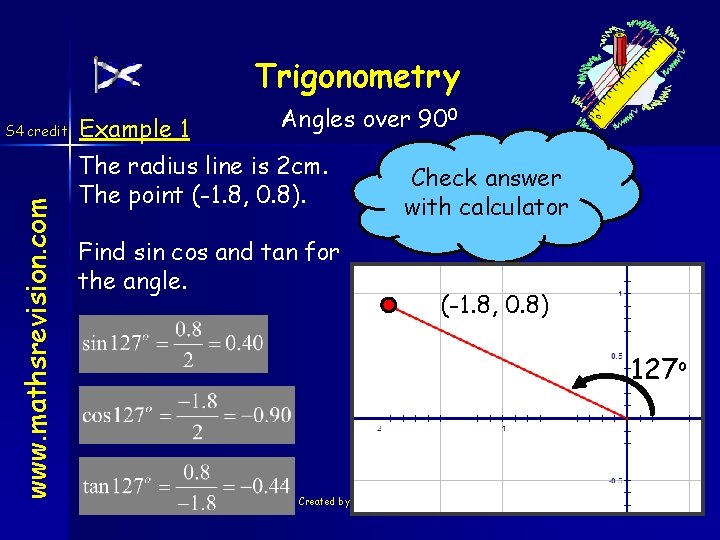
Trigonometry www. mathsrevision. com S 4 credit Example 1 Angles over 900 The radius line is 2 cm. The point (-1. 8, 0. 8). Find sin cos and tan for the angle. Check answer with calculator (-1. 8, 0. 8) 127 o 03 -Dec-20 Created by Mr Lafferty Maths Dept

Trigonometry www. mathsrevision. com S 4 credit All Quadrants Example Summary of results Calculate the ration for sin cos and tan for the angle values below. 30 o 45 o 60 o 120 o 135 o 150 o Sin x 03 -Dec-20 210 o 225 o 240 o 300 o 315 o 330 o Cos x 180 o 90 o Sin +ve All +ve 180 o - xo xo 180 o + xo 360 o - xo Tan +ve Cos +ve Tan x Created by Mr Lafferty Maths Dept 270 o 0 o

What Goes In The Box ? www. mathsrevision. com S 4 credit Write down the equivalent values of the following in term of the first quadrant (between 0 o and 90 o): 1) Sin 135 o sin 45 o 1) Sin 300 o - sin 60 o 2) Cos 150 o -cos 45 o 2) Cos 360 o cos 0 o 3) Tan 135 o -tan 45 o 3) Tan 330 o - tan 30 o 4) Sin 225 o -sin 45 o 4) Sin 380 o sin 20 o 5) Cos 270 o -cos 90 o 5) Cos 460 o - cos 80 o

Trigonometry Angles over 900 www. mathsrevision. com S 4 credit Now try MIA Ch 11 Ex 3. 1 Ch 11 (page 222) 03 -Dec-20 Created by Mr Lafferty Maths Dept

Starter www. mathsrevision. com S 4 Credit created by Mr. Lafferty

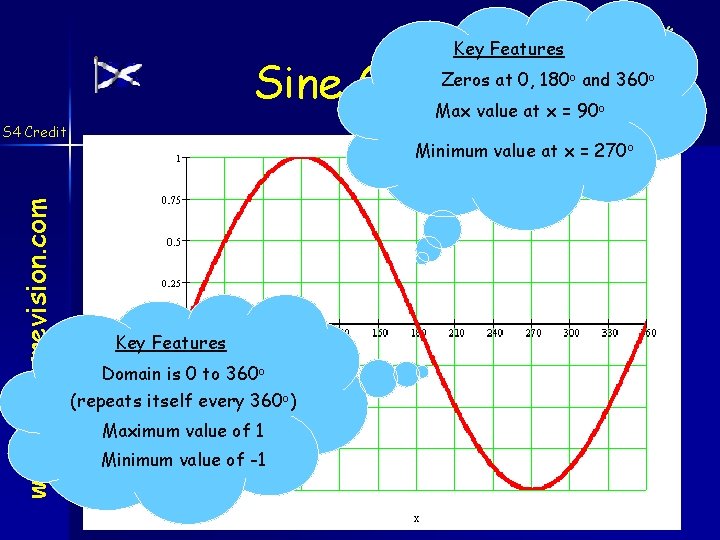
Sine Graph www. mathsrevision. com S 4 Credit Learning Intention Success Criteria 1. To investigate graphs of the form y = a sin xo y = a cos xo y = tan xo created by Mr. Lafferty 1. Identify the key points for various graphs.

Key Features Sine Graph Max value at x = 90 Zeros at 0, 180 o and 360 o www. mathsrevision. com S 4 Credit o Minimum value at x = 270 o Key Features Domain is 0 to 360 o (repeats itself every 360 o) Maximum value of 1 Minimum value of -1 created by Mr. Lafferty

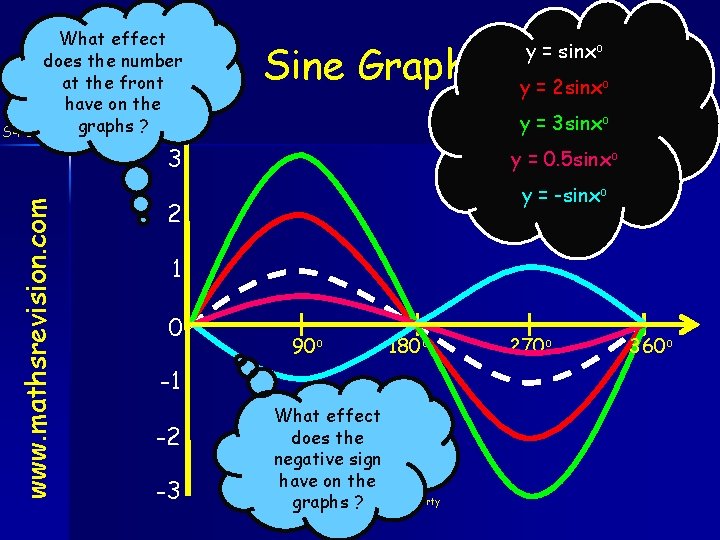
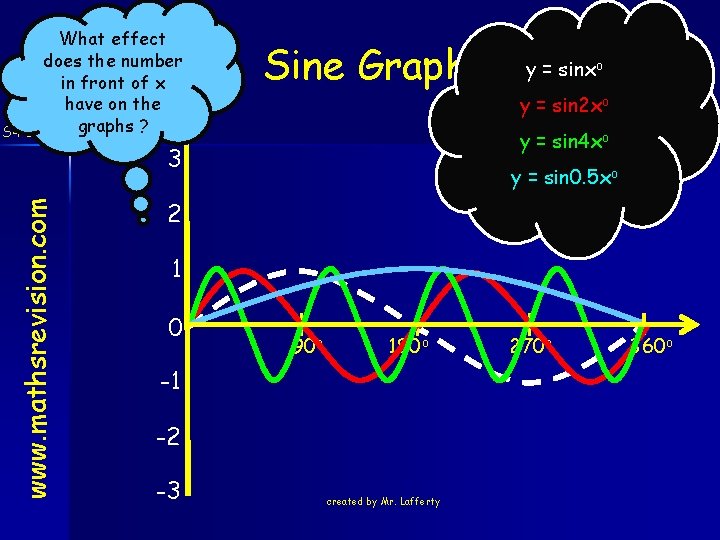
What effect does the number at the front have on the S 4 Credit graphs ? Sine Graph y = 2 sinxo y = 3 sinxo 3 www. mathsrevision. com y = sinxo y = 0. 5 sinxo y = -sinxo 2 1 0 90 o 180 o -1 -2 -3 What effect does the negative sign have on the created graphs ? by Mr. Lafferty 270 o 360 o

Sine Graph www. mathsrevision. com S 4 Credit y = a sin (x) For a > 1 stretches graph in the y-axis direction For a < 1 compresses graph in the y - axis direction For a - negative flips graph in the x – axis. created by Mr. Lafferty

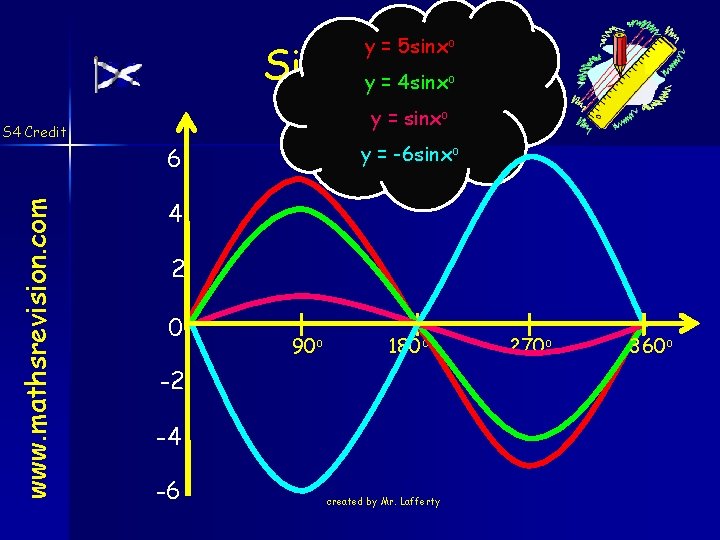
y = 5 sinxo Sine Graph y = 4 sinx o www. mathsrevision. com S 4 Credit y = sinxo y = -6 sinxo 6 4 2 0 90 o 180 o -2 -4 -6 created by Mr. Lafferty 270 o 360 o

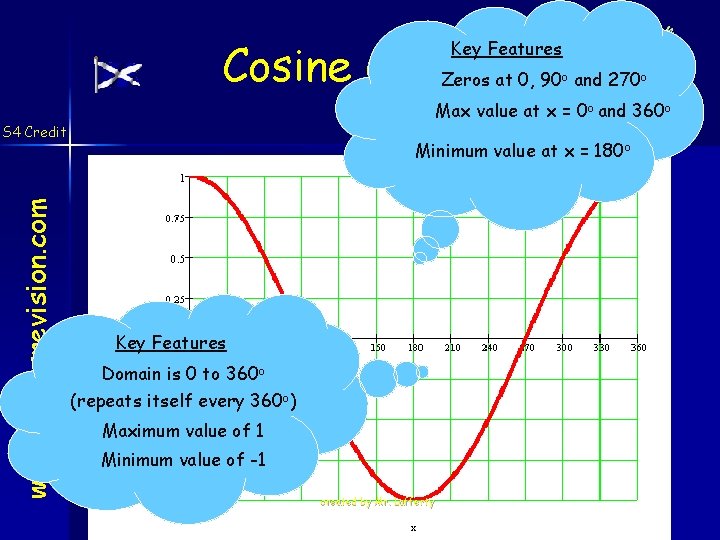
Cosine Graphs Zeros at 0, 90 and 270 Key Features o Max value at x = 0 o and 360 o S 4 Credit www. mathsrevision. com o Minimum value at x = 180 o Key Features Domain is 0 to 360 o (repeats itself every 360 o) Maximum value of 1 Minimum value of -1 created by Mr. Lafferty

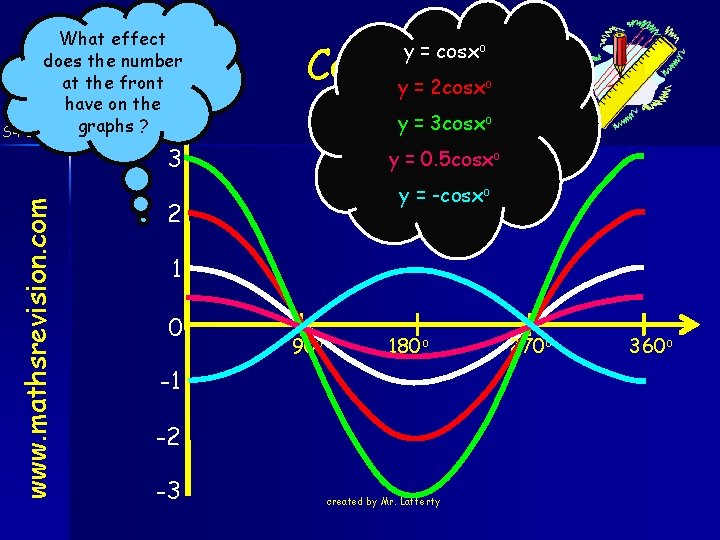
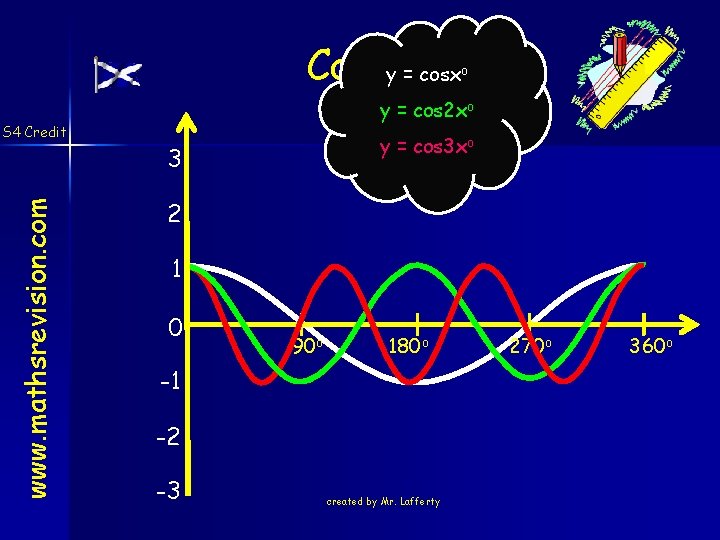
What effect does the number at the front have on the S 4 Credit graphs ? Cosine y = 2 cosx y = cosxo y = 3 cosxo 3 www. mathsrevision. com o y = 0. 5 cosxo y = -cosxo 2 1 0 90 o 180 o -1 -2 -3 created by Mr. Lafferty 270 o 360 o

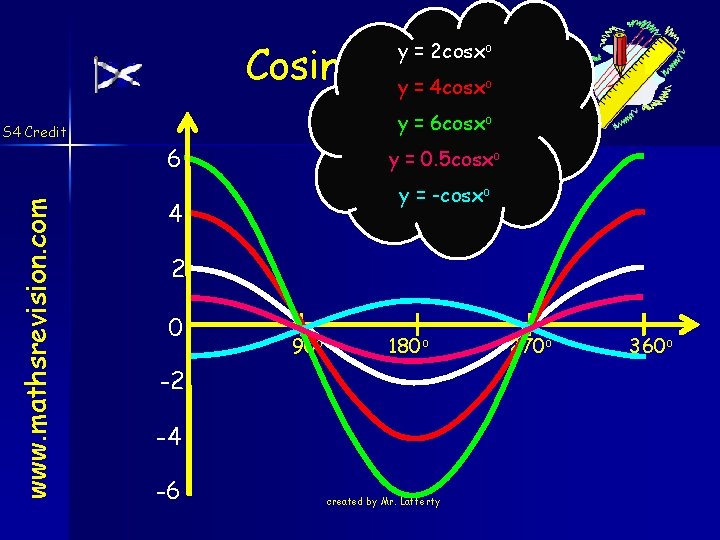
Cosine Graph y = 4 cosx y = 2 cosxo o www. mathsrevision. com S 4 Credit y = 6 cosxo 6 y = 0. 5 cosxo y = -cosxo 4 2 0 90 o 180 o -2 -4 -6 created by Mr. Lafferty 270 o 360 o

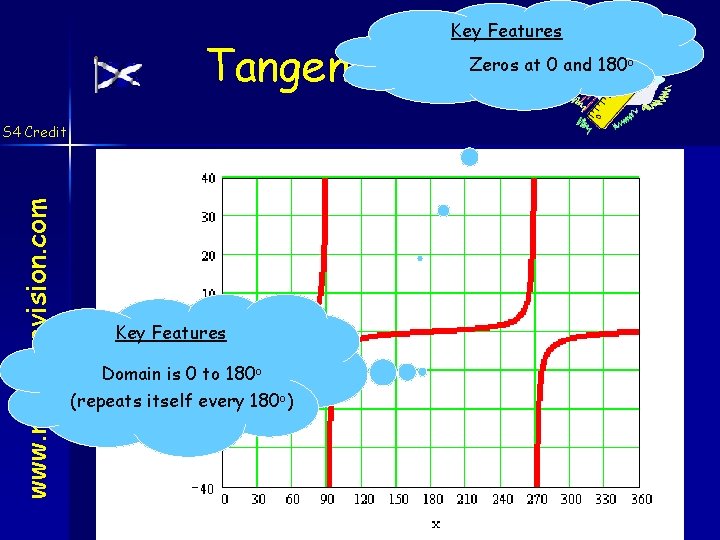
Key Features Tangent Graphs Zeros at 0 and 180 o www. mathsrevision. com S 4 Credit Key Features Domain is 0 to 180 o (repeats itself every 180 o) created by Mr. Lafferty

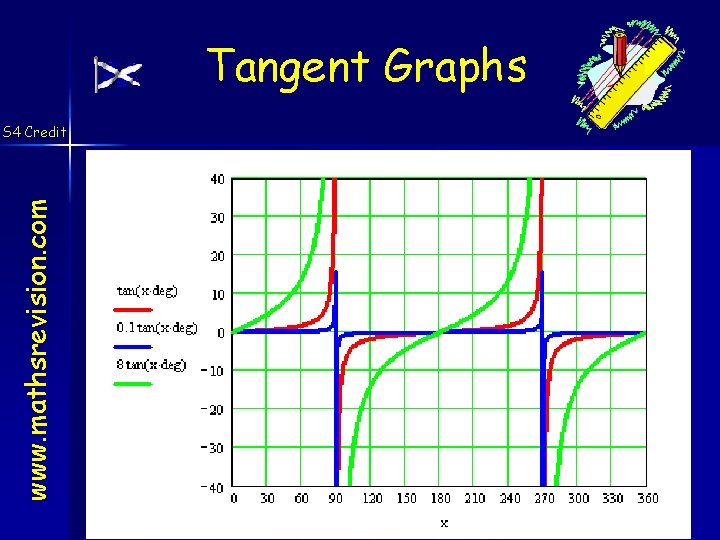
Tangent Graphs www. mathsrevision. com S 4 Credit created by Mr. Lafferty

Tangent Graph www. mathsrevision. com S 4 Credit y = a tan (x) For a > 1 stretches graph in the y-axis direction For a < 1 compresses graph in the y - axis direction For a - negative flips graph in the x – axis. created by Mr. Lafferty

Period of a Function www. mathsrevision. com S 4 Credit When a pattern repeats itself over and over, it is said to be periodic. Sine function has a period of 360 o Let’s investigate the function y = sin bx created by Mr. Lafferty

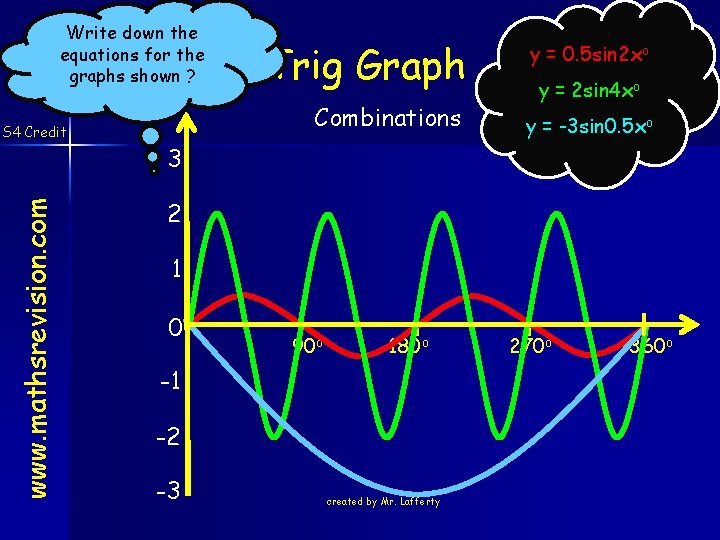
What effect does the number in front of x have on the S 4 Credit graphs ? Sine Graph y = sin 2 xo y = sin 4 xo 3 www. mathsrevision. com y = sinxo y = sin 0. 5 xo 2 1 0 90 o 180 o -1 -2 -3 created by Mr. Lafferty 270 o 360 o

Trigonometry Graphs www. mathsrevision. com S 4 Credit y = a sin (bx) How many times it repeats itself in 360 o For a > 1 stretches graph in the y-axis direction For a < 1 compresses graph in the y - axis direction For a - negative flips graph in the x – axis. created by Mr. Lafferty

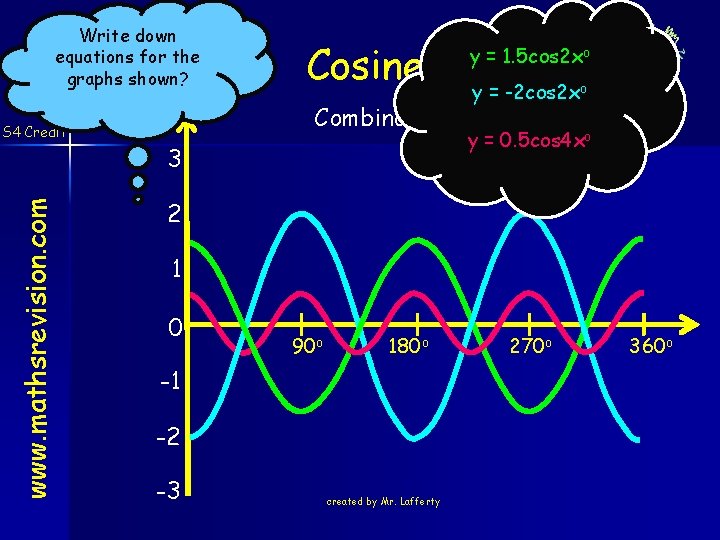
Cosine y = cosx www. mathsrevision. com S 4 Credit o y = cos 2 xo y = cos 3 xo 3 2 1 0 90 o 180 o -1 -2 -3 created by Mr. Lafferty 270 o 360 o

Trigonometry Graphs www. mathsrevision. com S 4 Credit y = a cos (bx) How many times it repeats itself in 360 o For a > 1 stretches graph in the y-axis direction For a < 1 compresses graph in the y - axis direction For a - negative flips graph in the x – axis. created by Mr. Lafferty

Trigonometry Graphs www. mathsrevision. com S 4 Credit y = a tan (bx) How many times it repeats itself in 180 o For a > 1 stretches graph in the y-axis direction For a < 1 compresses graph in the y - axis direction For a - negative flips graph in the x – axis. created by Mr. Lafferty

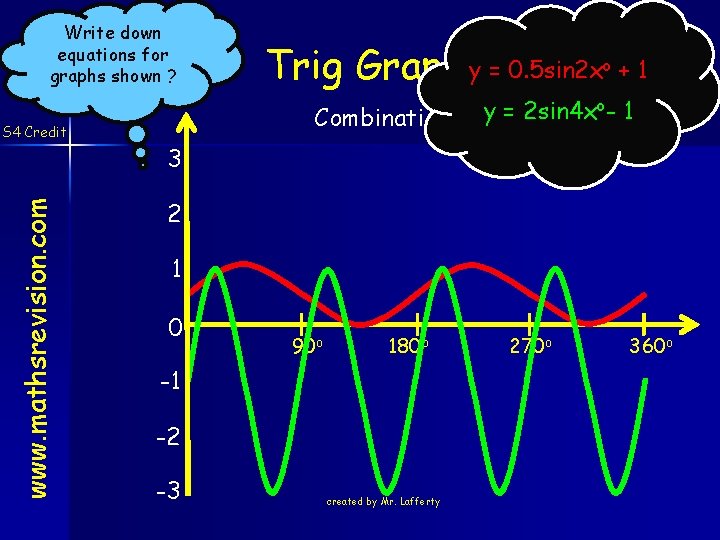
Write down the equations for the graphs shown ? www. mathsrevision. com S 4 Credit Trig Graph Combinations y = 0. 5 sin 2 xo y = 2 sin 4 xo y = -3 sin 0. 5 xo 3 2 1 0 90 o 180 o -1 -2 -3 created by Mr. Lafferty 270 o 360 o

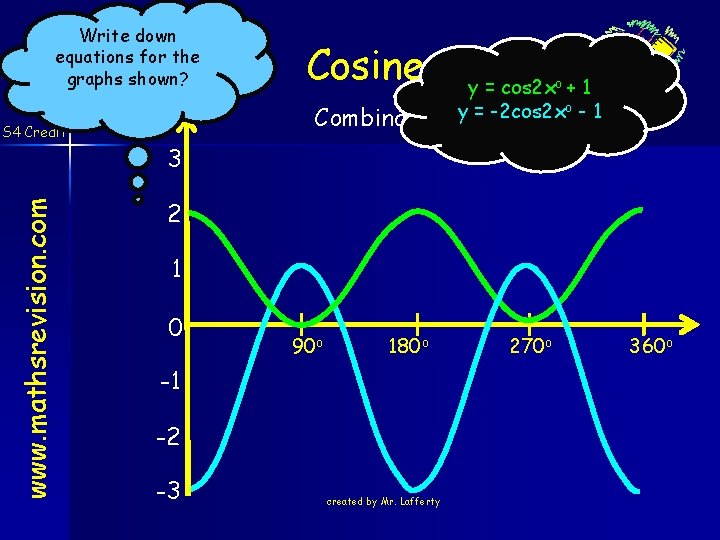
Write down equations for the graphs shown? www. mathsrevision. com S 4 Credit Cosine Combinations 3 y = 1. 5 cos 2 xo y = -2 cos 2 xo y = 0. 5 cos 4 xo 2 1 0 90 o 180 o -1 -2 -3 created by Mr. Lafferty 270 o 360 o

Combination Graphs www. mathsrevision. com S 4 Credit Now Try MIA Ch 11 Ex 5. 1 Page 227 created by Mr. Lafferty

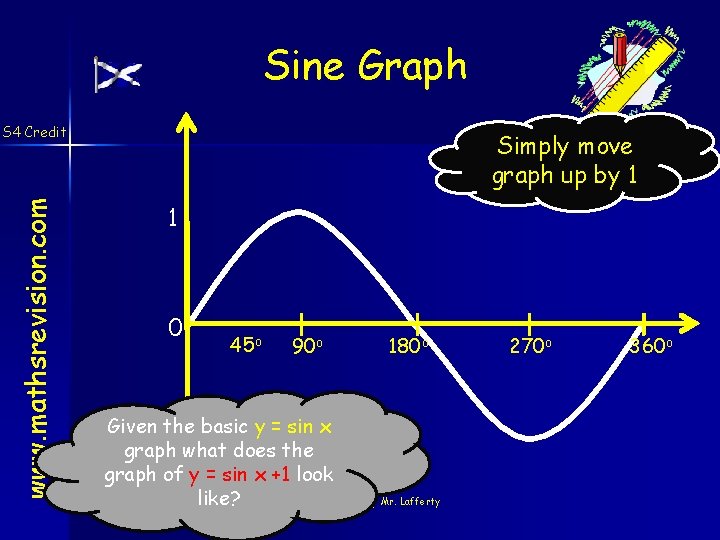
Sine Graph www. mathsrevision. com S 4 Credit Simply move graph up by 1 1 0 45 o 90 o 180 o Given the basic y = sin x -1 graph what does the graph of y = sin x +1 look created by Mr. Lafferty like? 270 o 360 o

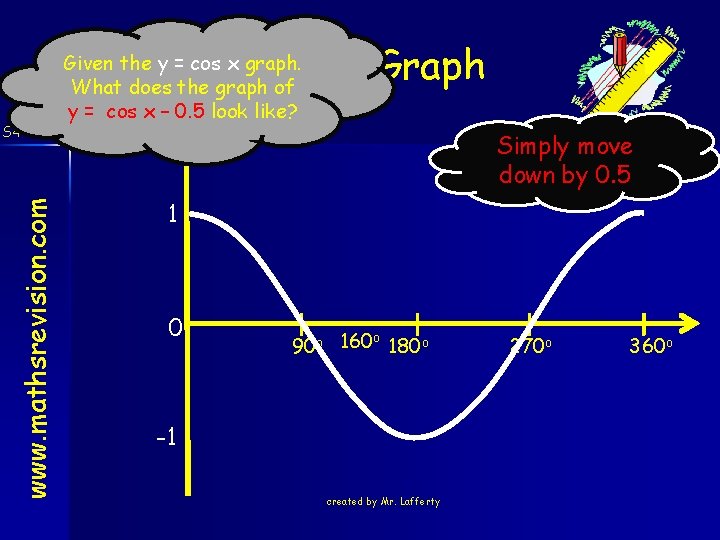
Cosine Graph Given the y = cos x graph. What does the graph of y = cos x – 0. 5 look like? www. mathsrevision. com S 4 Credit Simply move down by 0. 5 1 0 o 90 o 160 180 o -1 created by Mr. Lafferty 270 o 360 o

Write down equations for graphs shown ? www. mathsrevision. com S 4 Credit Trig Graph y = 0. 5 sin 2 x o +1 o- 1 y = 2 sin 4 x Combinations 3 2 1 0 90 o 180 o -1 -2 -3 created by Mr. Lafferty 270 o 360 o

Write down equations for the graphs shown? www. mathsrevision. com S 4 Credit Cosine y = cos 2 xo + 1 o Combinationsy = -2 cos 2 x - 1 3 2 1 0 90 o 180 o -1 -2 -3 created by Mr. Lafferty 270 o 360 o

Combination Graphs www. mathsrevision. com S 4 Credit Now try MIA Ch 11 Ex 5. 2 Page 227 created by Mr. Lafferty

Starter www. mathsrevision. com S 4 Credit created by Mr. Lafferty

Solving Trig Equations www. mathsrevision. com S 4 Credit Learning Intention Success Criteria 1. To explain how to solve trig equations of the form a sin xo + 1 = 0 created by Mr. Lafferty 1. Use the rule for solving any ‘ normal ‘ equation 2. Realise that there are many solutions to trig equations depending on domain.

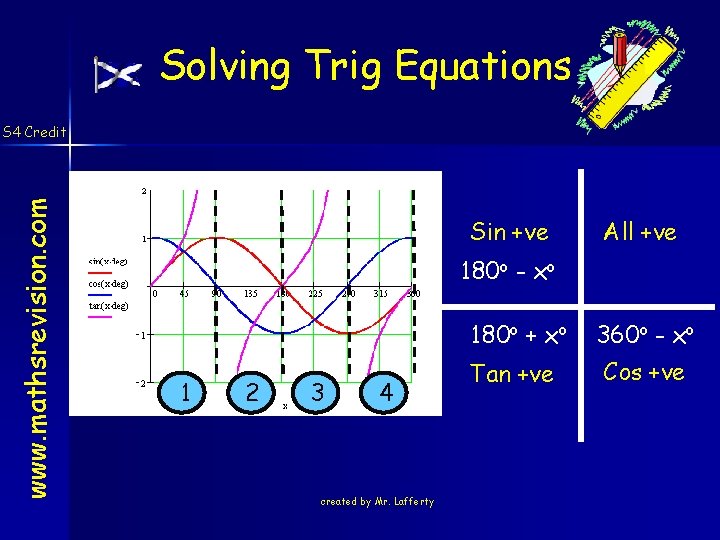
Solving Trig Equations www. mathsrevision. com S 4 Credit Sin +ve All +ve 180 o - xo 1 2 3 4 created by Mr. Lafferty 180 o + xo 360 o - xo Tan +ve Cos +ve

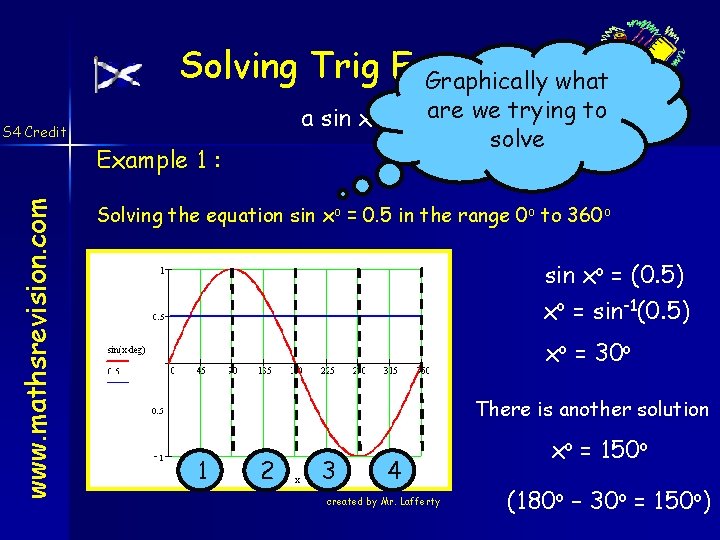
Solving Trig Equations Graphically what a sin xo + b are = 0 we trying to solve S 4 Credit www. mathsrevision. com Example 1 : Solving the equation sin xo = 0. 5 in the range 0 o to 360 o sin xo = (0. 5) xo = sin-1(0. 5) xo = 30 o There is another solution 1 2 3 4 created by Mr. Lafferty xo = 150 o (180 o – 30 o = 150 o)

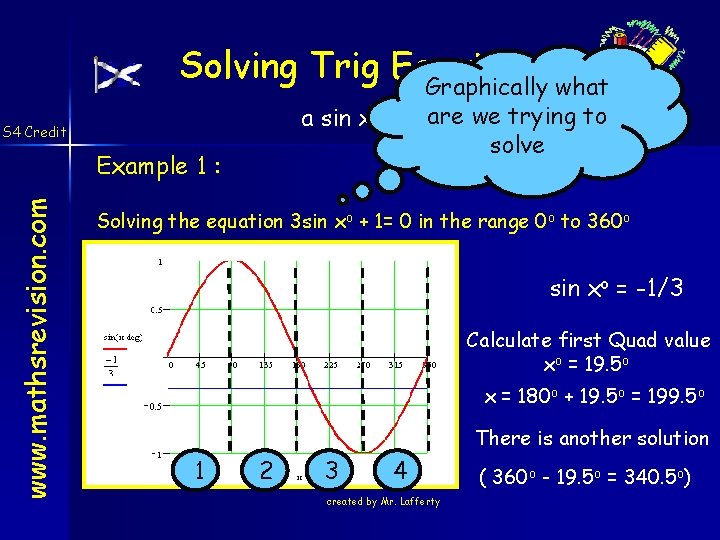
Solving Trig Equations Graphically what a sin xo + b are = 0 we trying to solve S 4 Credit www. mathsrevision. com Example 1 : Solving the equation 3 sin xo + 1= 0 in the range 0 o to 360 o sin xo = -1/3 Calculate first Quad value xo = 19. 5 o x = 180 o + 19. 5 o = 199. 5 o There is another solution 1 2 3 4 created by Mr. Lafferty ( 360 o - 19. 5 o = 340. 5 o)

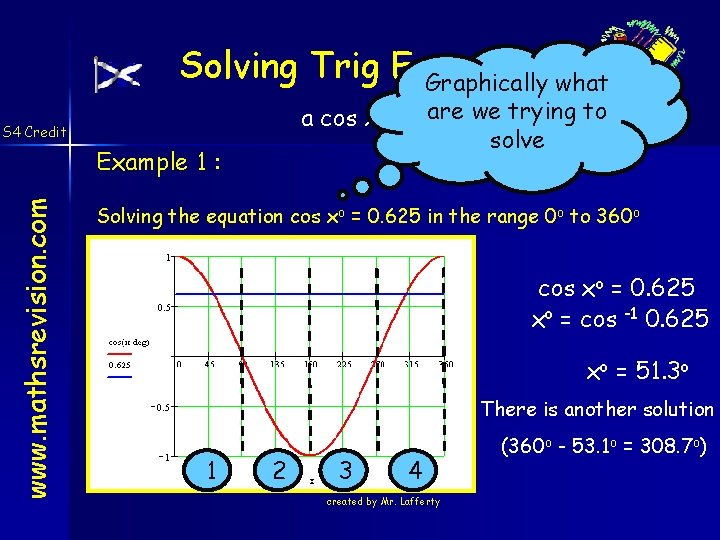
Solving Trig Equations Graphically what a cos xo + b are = 0 we trying to solve S 4 Credit www. mathsrevision. com Example 1 : Solving the equation cos xo = 0. 625 in the range 0 o to 360 o cos xo = 0. 625 xo = cos -1 0. 625 xo = 51. 3 o There is another solution 1 2 3 4 created by Mr. Lafferty (360 o - 53. 1 o = 308. 7 o)

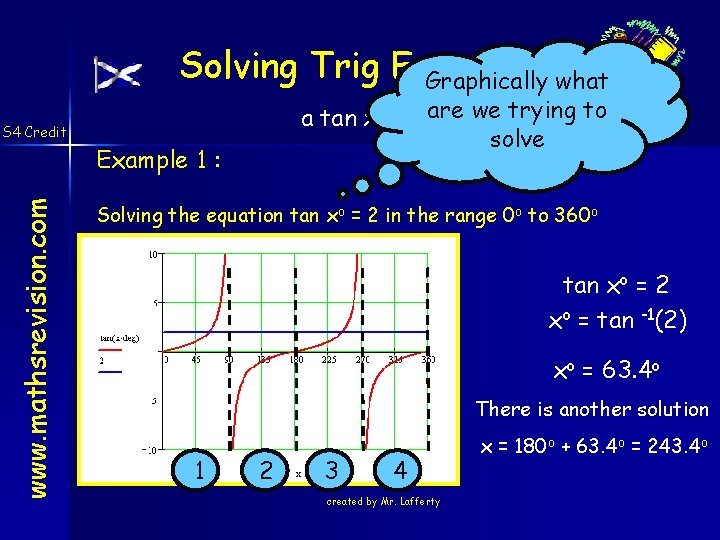
Solving Trig Equations Graphically what a tan xo + b are = 0 we trying to solve S 4 Credit www. mathsrevision. com Example 1 : Solving the equation tan xo = 2 in the range 0 o to 360 o tan xo = 2 xo = tan -1(2) xo = 63. 4 o There is another solution 1 2 3 4 created by Mr. Lafferty x = 180 o + 63. 4 o = 243. 4 o

Solving Trig Equations www. mathsrevision. com S 4 Credit Now try MIA Ch 11 Ex 6. 1, 6. 2 and 7. 1 (page 236) created by Mr. Lafferty

Starter www. mathsrevision. com S 4 Credit created by Mr. Lafferty

Solving Trig Equations www. mathsrevision. com S 4 Credit Learning Intention Success Criteria 1. To explain some special trig relationships sin 2 xo + cos 2 xo = ? and tan xo and sin x cos x created by Mr. Lafferty 1. Know and learn the two special trig relationships. 2. Apply them to solve problems.

Solving Trig Equations www. mathsrevision. com S 4 Credit Lets investigate sin 2 xo + cos 2 xo = ? Calculate value for x = 10, 20, 50, 250 sin 2 xo + cos 2 xo = 1 created by Mr. Lafferty Learn !

Solving Trig Equations www. mathsrevision. com S 4 Credit Lets investigate tan xo and sin xo cos xo Calculate value for x = 10, 20, 50, 250 tan xo = sin xo cos xo created by Mr. Lafferty Learn !

Solving Trig Equations www. mathsrevision. com S 4 Credit Now try MIA Ex 8. 1 Ch 11 (page 238) created by Mr. Lafferty