TRIGONOMETRY GENERAL MATHS UNIT TWO RIGHT ANGLED TRIANGLES

TRIGONOMETRY GENERAL MATHS UNIT TWO

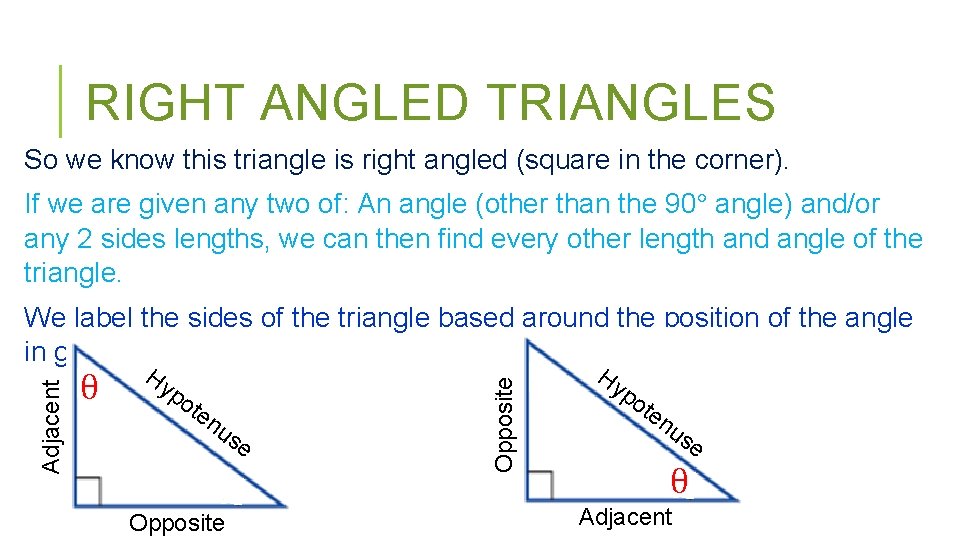
RIGHT ANGLED TRIANGLES – BACKGROUND INFO The internal angles within the triangle add up to 180° The square in the corner of the triangle means that the angle here is 90° and means that this is a right angled triangle This means that the other 2 angles add up to 90°

RIGHT ANGLED TRIANGLES So we know this triangle is right angled (square in the corner). If we are given any two of: An angle (other than the 90° angle) and/or any 2 sides lengths, we can then find every other length and angle of the triangle. θ Hy po te nu s Opposite e Opposite Adjacent We label the sides of the triangle based around the position of the angle in given in a problem. Hy po te nu se θ Adjacent

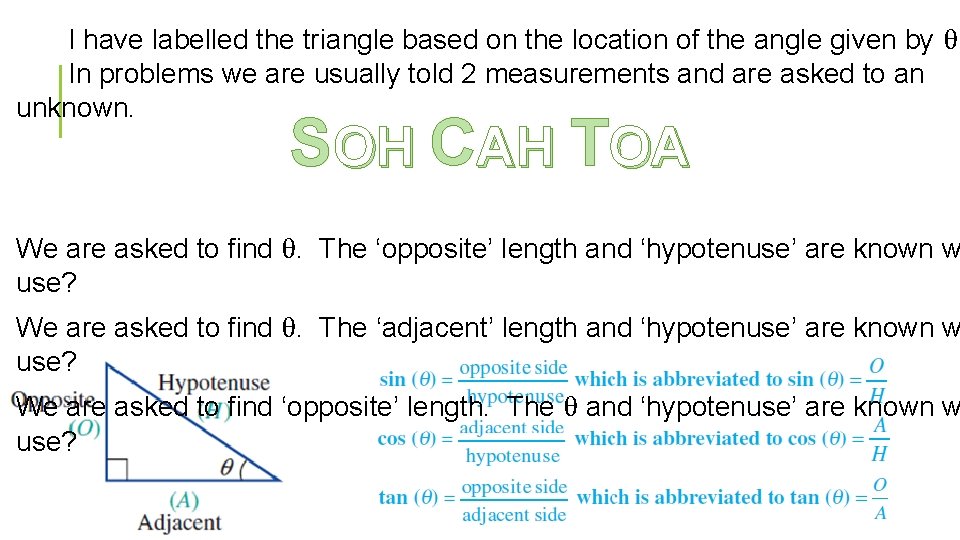
I have labelled the triangle based on the location of the angle given by θ In problems we are usually told 2 measurements and are asked to an unknown. SOH CAH TOA We are asked to find θ. The ‘opposite’ length and ‘hypotenuse’ are known w use? We are asked to find θ. The ‘adjacent’ length and ‘hypotenuse’ are known w use? We are asked to find ‘opposite’ length. The θ and ‘hypotenuse’ are known w use?

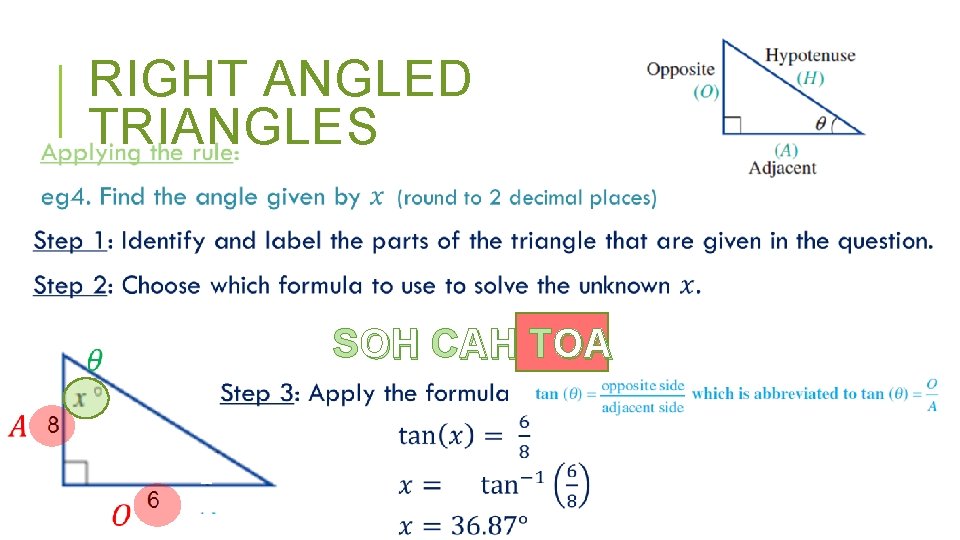
RIGHT ANGLED TRIANGLES SOH CAH TOA

RIGHT ANGLED TRIANGLES SOH CAH TOA

RIGHT ANGLED TRIANGLES SOH CAH TOA

RIGHT ANGLED TRIANGLES SOH CAH TOA

NOW DO EXERCISE 7 A Questions 1, 2 AFG, 3 ABJ, 7, 10, 11, 13, 15, 16, 19

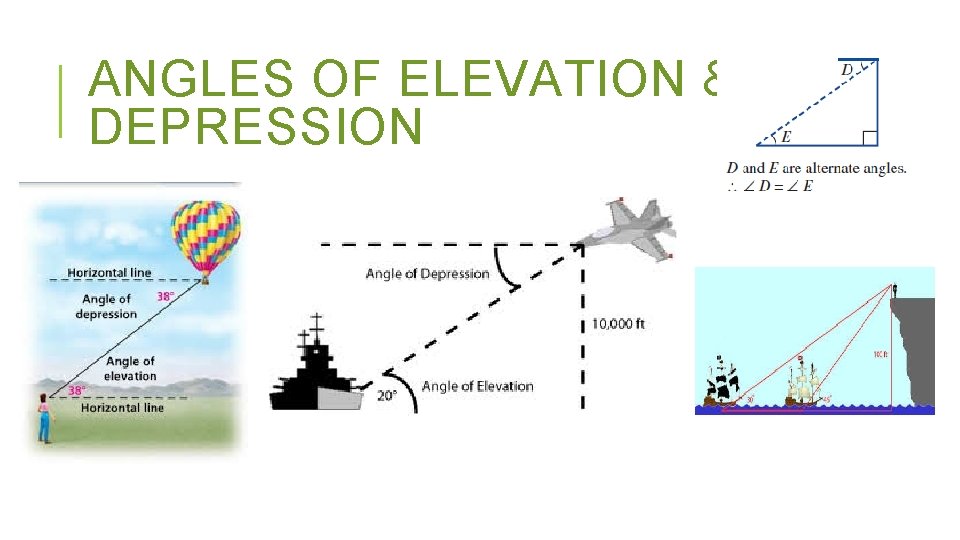
ANGLES OF ELEVATION & DEPRESSION Angles of Elevation and Depression are used when dealing with directions which require us to look up or down at something. and an The angle of elevation is the angle between the horizontal an object which is higher than the observer. (eg. The top of a mountain or flagpole) The angle of depression is the angle between the horizontal and an object which is lower than the observer.

ANGLES OF ELEVATION & DEPRESSION

ANGLES OF ELEVATION & DEPRESSION

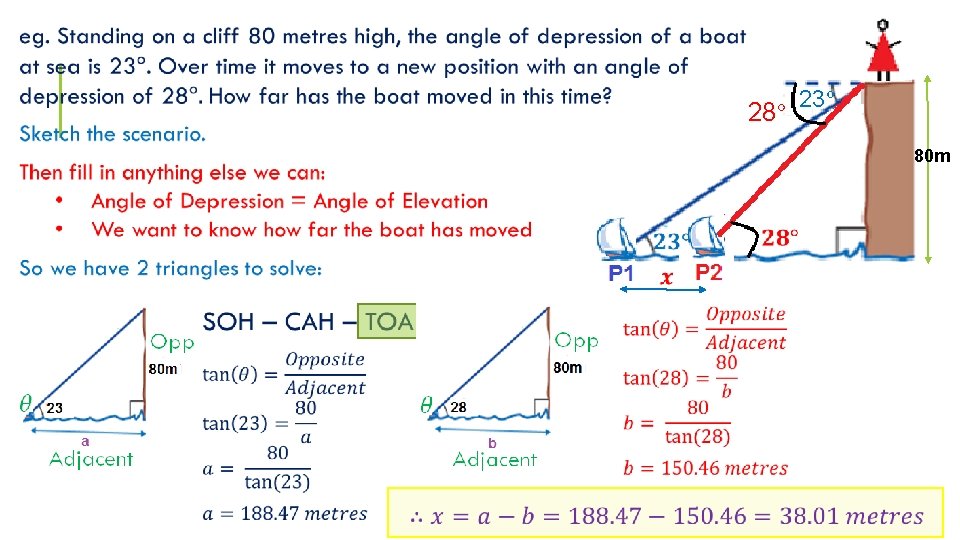
ANGLES OF ELEVATION & DEPRESSION 50 m Opposite Adjacent

28° 23° 80 m

NOW DO EXERCISE 7 B Questions 1 -8

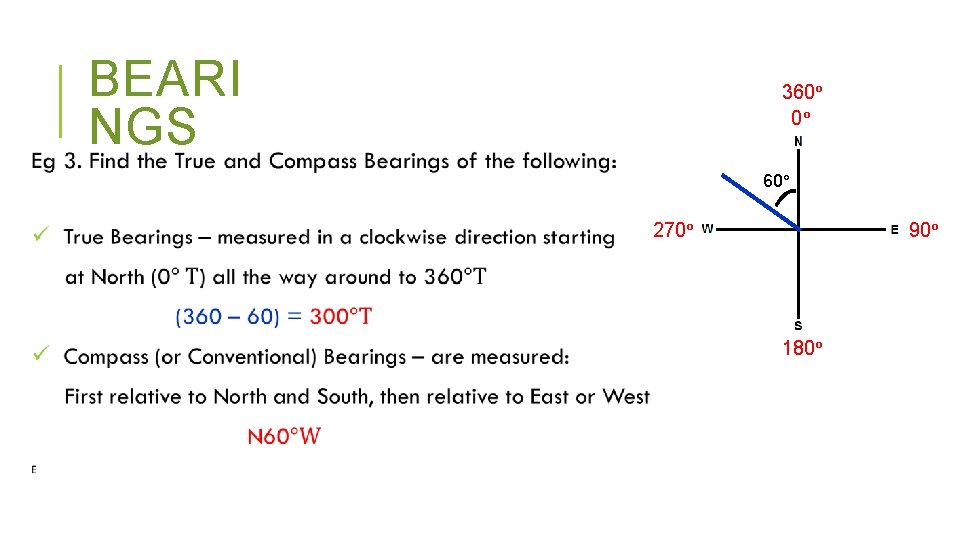
BEARI NGS 360° 0° 40° 270° 90° 180°

BEARI NGS 360° 0° 270° 90° 30° 180°

BEARI NGS 360° 0° 60° 270° 90° 180°

BEARI NGS 360° 0° 270° 90° 70° 180°

BEARI NGS 360° 0° 270° 90° 75° 180°

BEARI NGS 360° 0° 25° 270° 180° 90°

BEARINGS APPLICATIONS Eg 1. A ship sails 20 km in a direction of N 60°W. How far West from the starting point has the ship sailed? Step 1: Draw a diagram of the situation, labelling compass points and the given information Step 2: Find the triangle that we are interested in and label H, O, A, θ O Step 3: Decide which rule to apply & solve the problem Θ = 60° Hypotenuse = 20 km Opposite = ? H θ

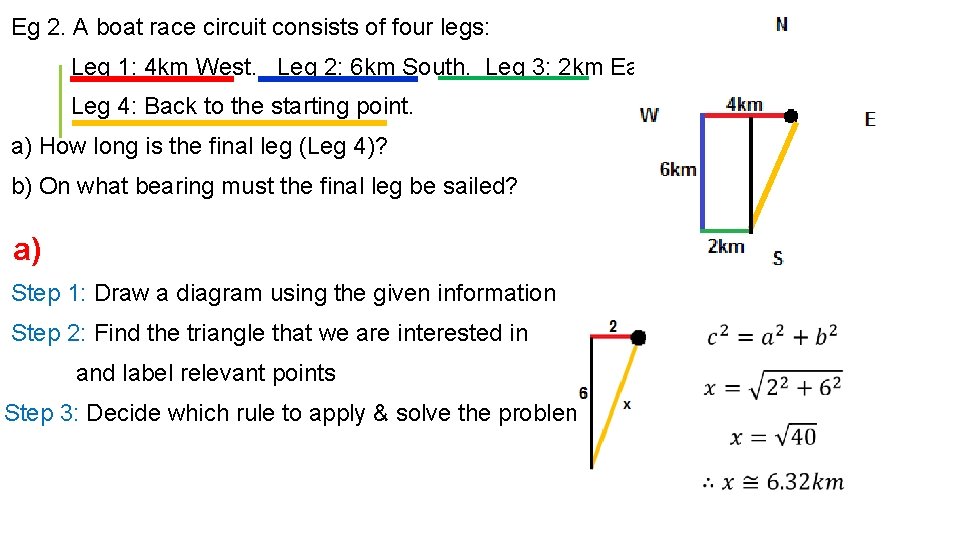
Eg 2. A boat race circuit consists of four legs: Leg 1: 4 km West. Leg 2: 6 km South. Leg 3: 2 km East. Leg 4: Back to the starting point. a) How long is the final leg (Leg 4)? b) On what bearing must the final leg be sailed? a) Step 1: Draw a diagram using the given information Step 2: Find the triangle that we are interested in and label relevant points Step 3: Decide which rule to apply & solve the problem

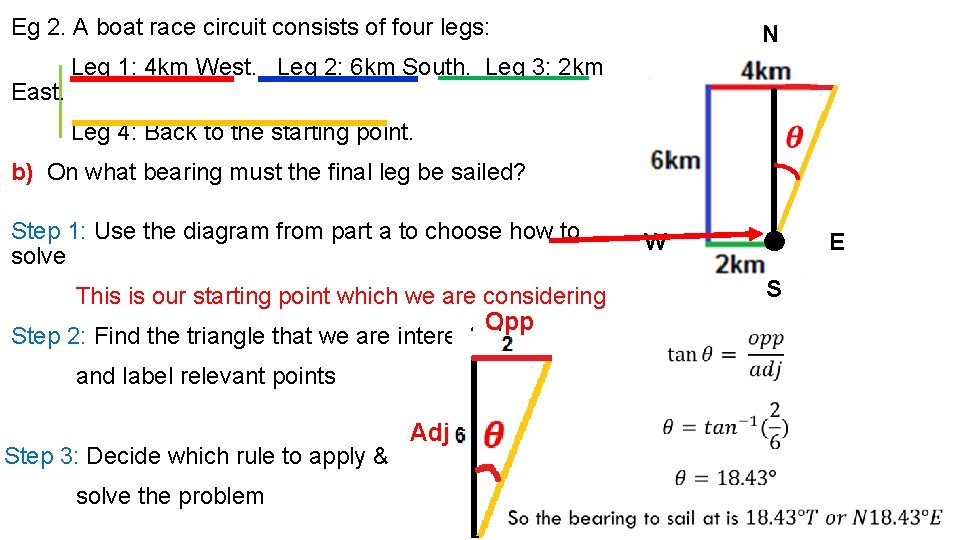
Eg 2. A boat race circuit consists of four legs: East. N Leg 1: 4 km West. Leg 2: 6 km South. Leg 3: 2 km Leg 4: Back to the starting point. b) On what bearing must the final leg be sailed? Step 1: Use the diagram from part a to choose how to solve This is our starting point which we are considering Opp Step 2: Find the triangle that we are interested in and label relevant points Step 3: Decide which rule to apply & solve the problem Adj E W S

NOW DO EXERCISE 7 B Questions 10 – 18; 20

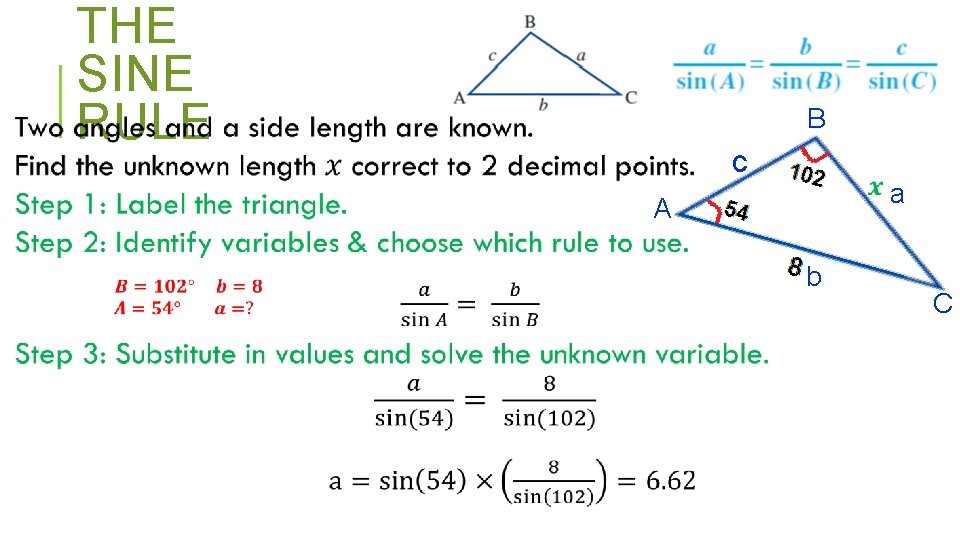
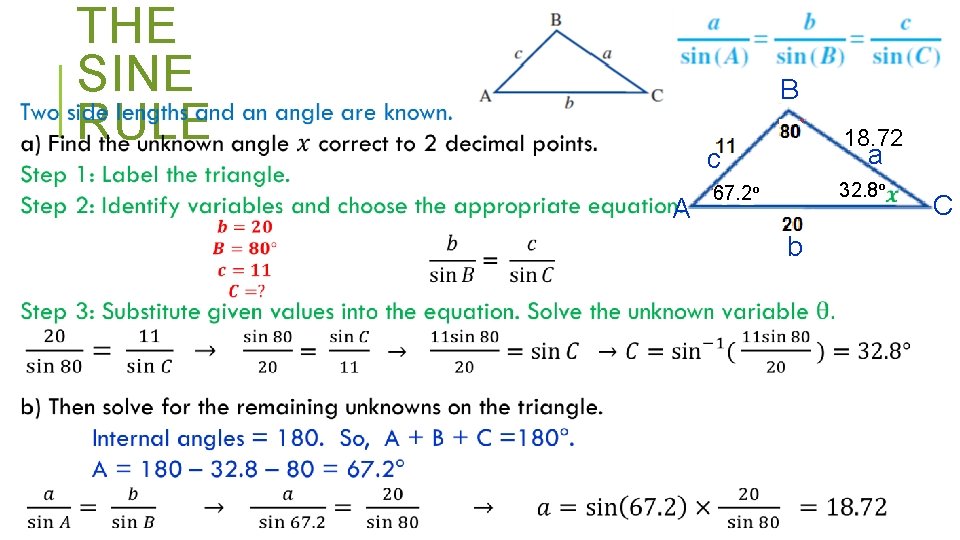
NON RIGHT ANGLED TRIANGLES THE RULE So far we have been solving-right angled. SINE triangles (where one corner is 90°). Now we look at solving every other triangle. The internal angles still add up to 180°. One method is the sine rule

THE SINE RULE B c a A b C

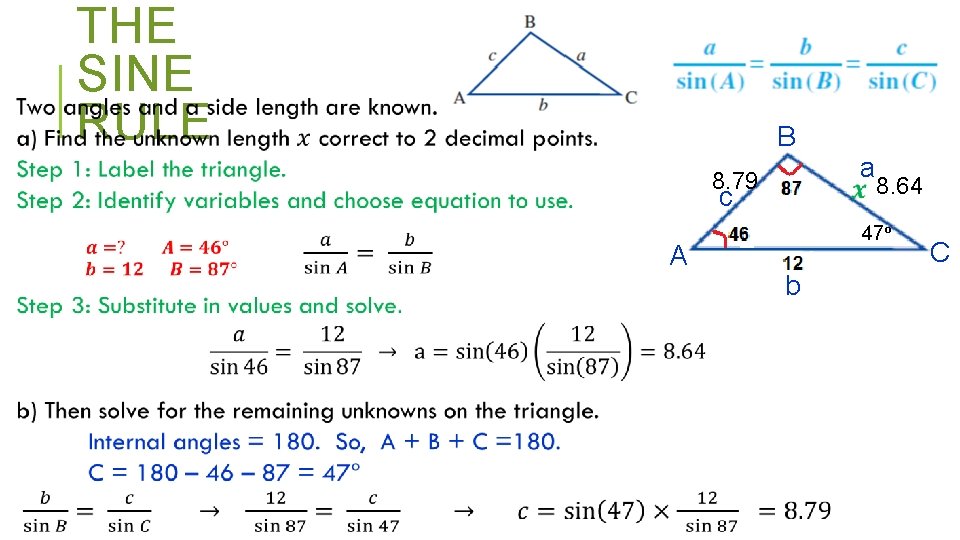
THE SINE RULE B a 8. 79 c A 8. 64 47° b C

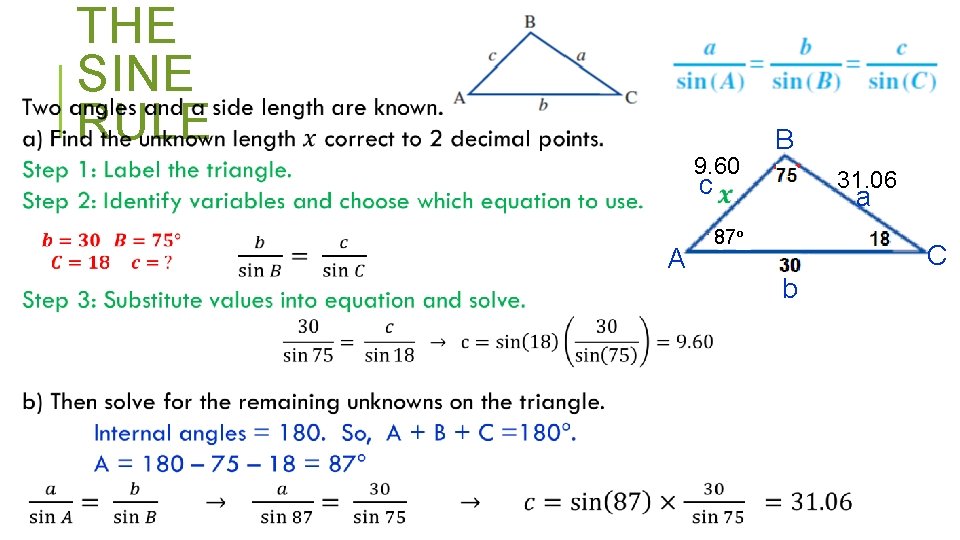
THE SINE RULE 9. 60 B 31. 06 c A a 87° C b

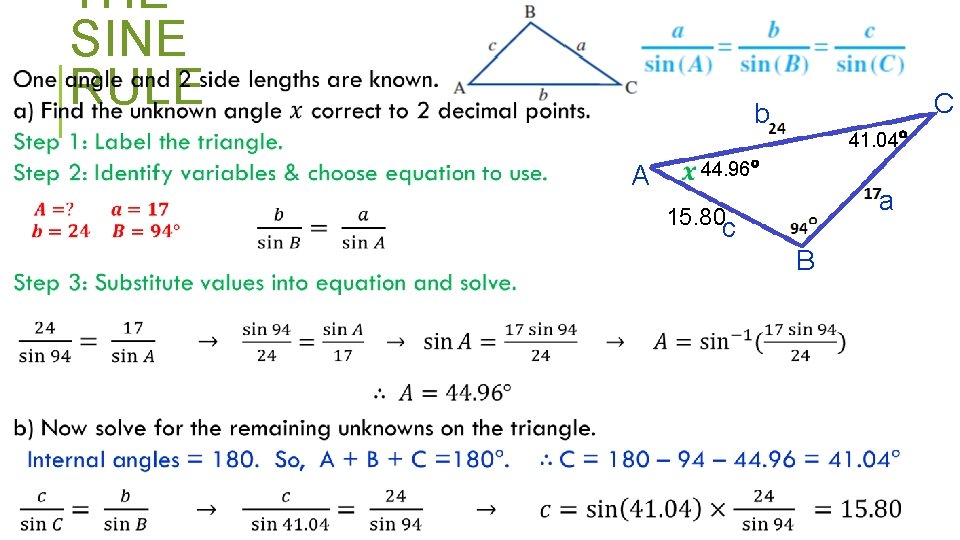
THE SINE RULE C b A 41. 04° 44. 96° a 15. 80 c B

THE SINE RULE B 18. 72 a c A 32. 8° 67. 2° b C

NOW DO EXERCISE 7 C Questions 1 - 3; 6 - 8; 12, 14, 18, 21

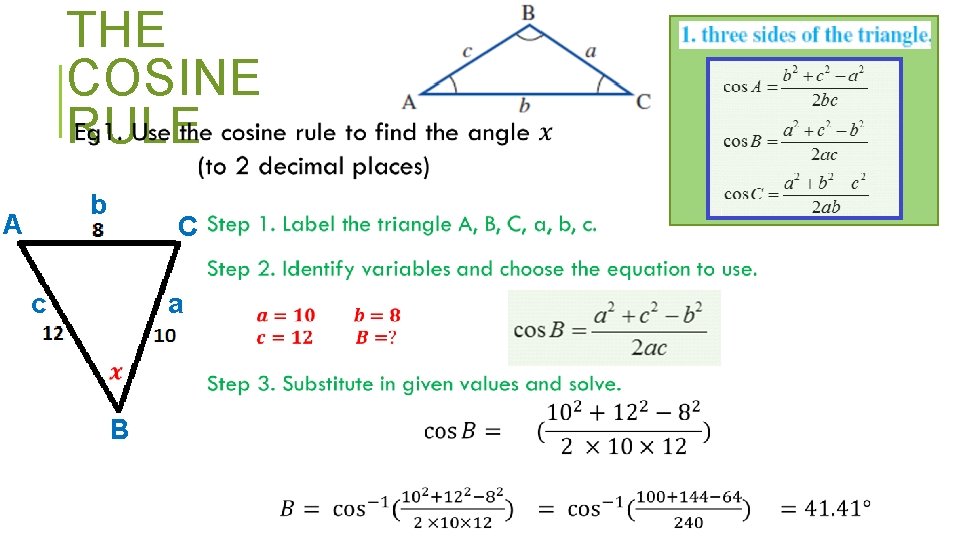
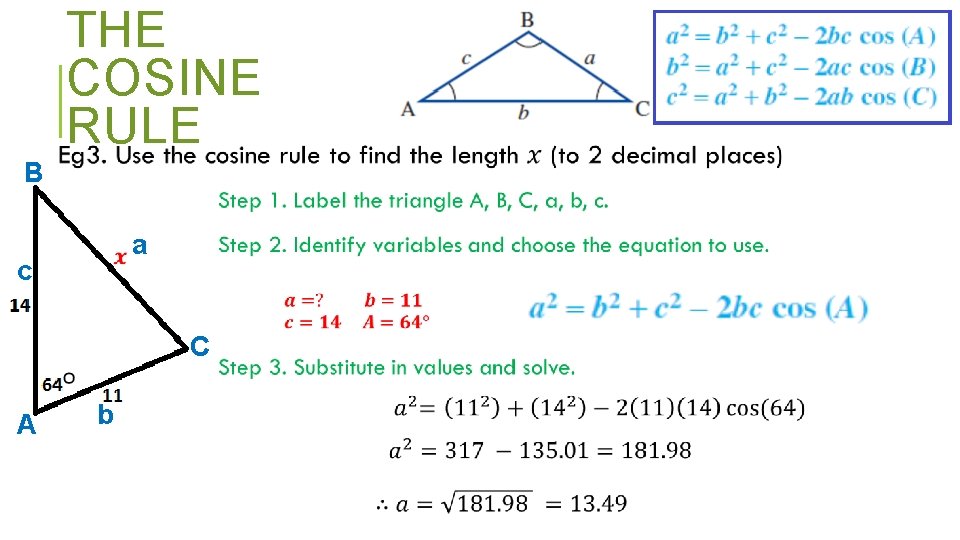
NON RIGHT ANGLED TRIANGLES - THE COSINE RULE

THE COSINE RULE b A C c a B

THE COSINE RULE B c a A b C

THE COSINE RULE B a c C A b

a) B C 5. 57 c a A b b)

NOW DO EXERCISE 7 D Questions 1 – 9 & 13.

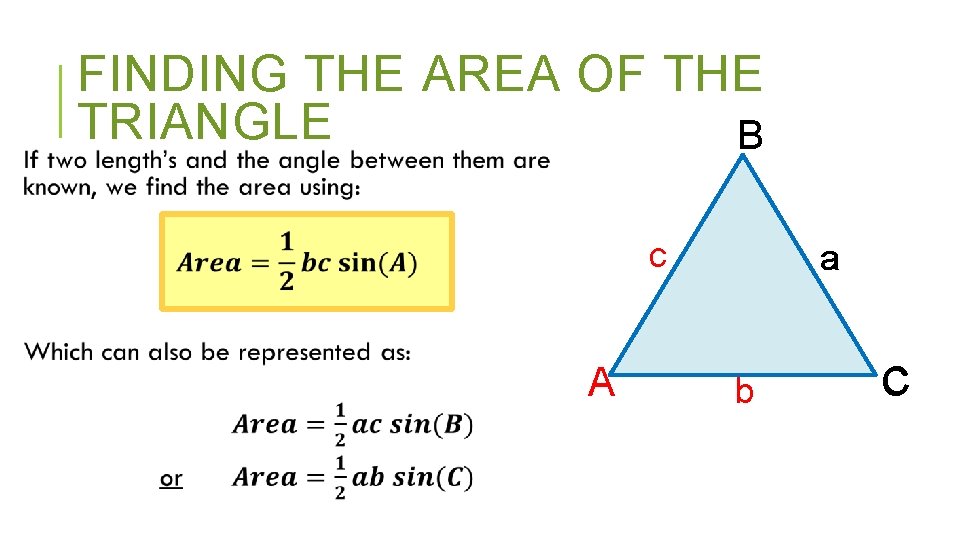
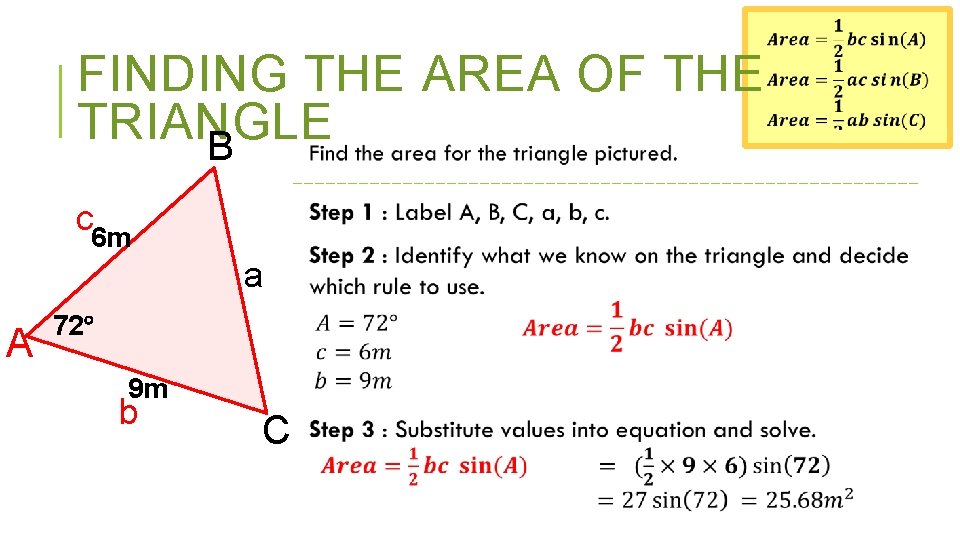
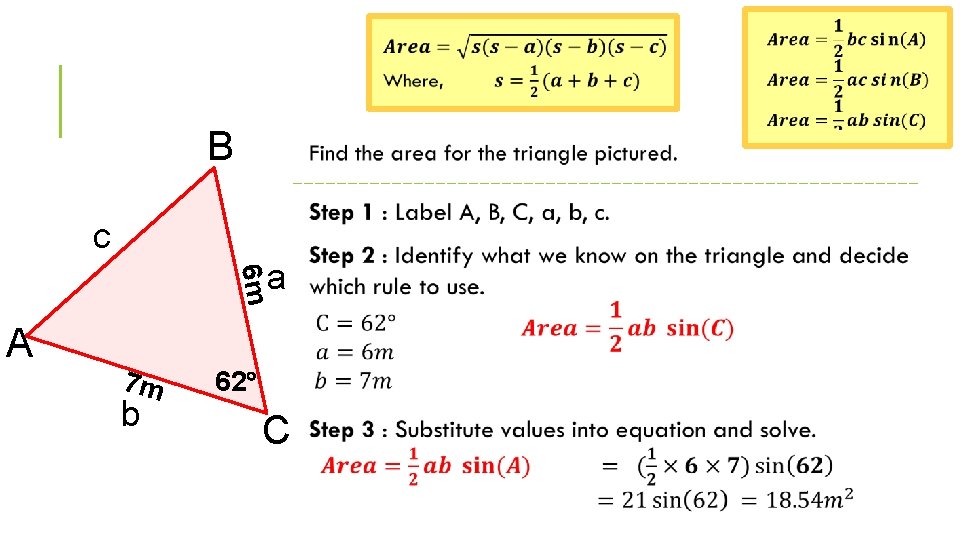
FINDING THE AREA OF THE TRIANGLE B c A a b C

FINDING THE AREA OF THE TRIANGLE B c 6 m a A 72° 9 m b C

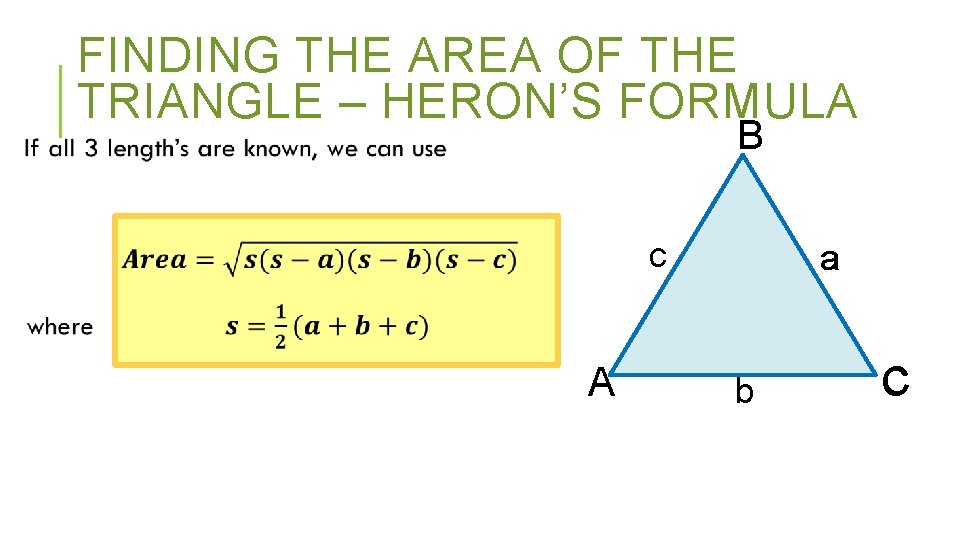
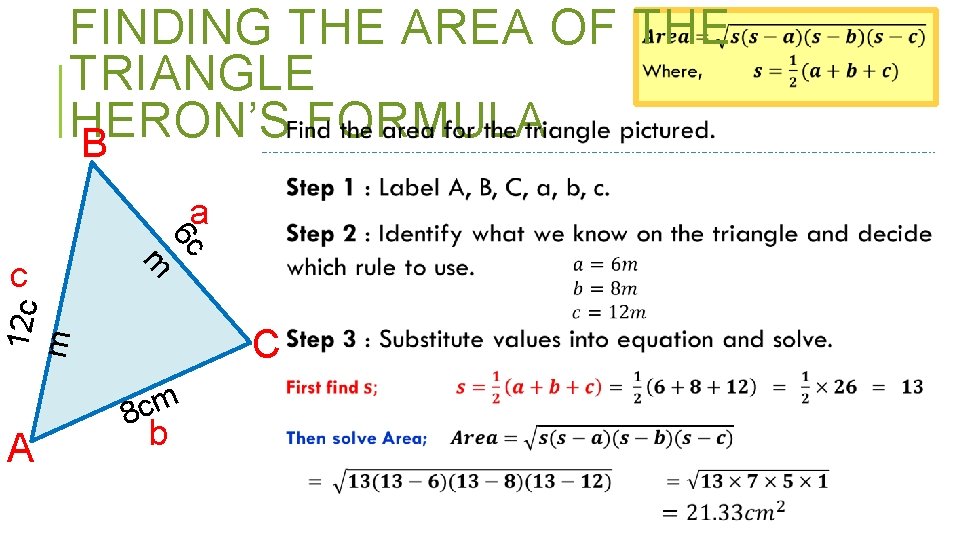
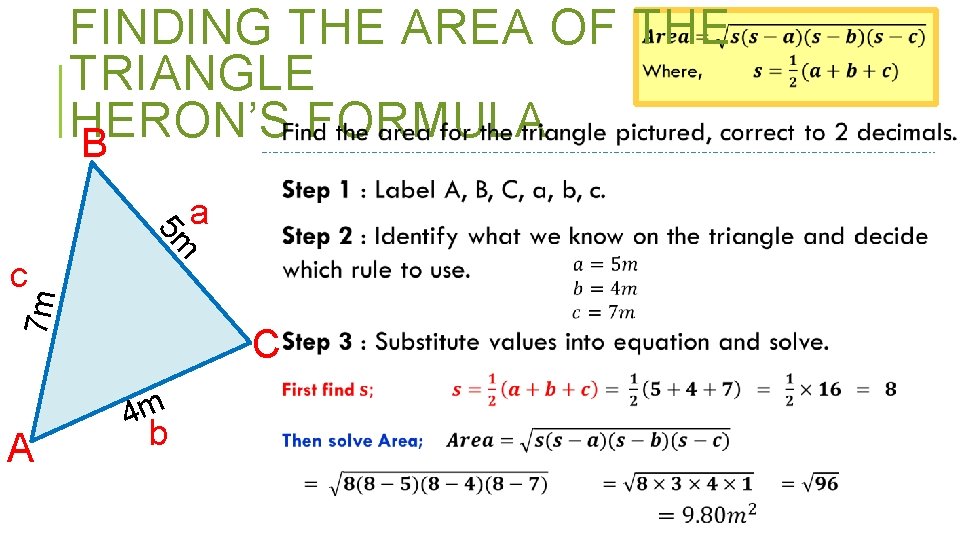
FINDING THE AREA OF THE TRIANGLE – HERON’S FORMULA B c A a b C

FINDING THE AREA OF THE TRIANGLE HERON’S FORMULA B a 6 c 12 c m m c A C 8 cm b

FINDING THE AREA OF THE TRIANGLE HERON’S FORMULA B 7 m c 5 m a A C 4 m b

B c 6 m a A 7 m b 62° C

NOW DO EXERCISE 7 E Questions 1, 3, 8, 10, 12, 15, 16, 18 – 20