TRIGONOMETRY Find trigonometric ratios using right triangles Solve

TRIGONOMETRY • Find trigonometric ratios using right triangles • Solve problems using trigonometric ratios Sextant

TRIGONOMETRIC RATIOS TRIGONOMETRY comes from two Greek terms: – trigon, meaning triangle – metron, meaning measure

TRIGONOMETRIC RATIOS TRIGONOMETRY comes from two Greek terms: – trigon, meaning triangle – metron, meaning measure A ratio of the lengths of sides of a right triangle is called a TRIGONOMETRIC RATIO.

TRIGONOMETRIC RATIOS The three most common trigonometric ratios are: • Sine • Cosine • Tangent

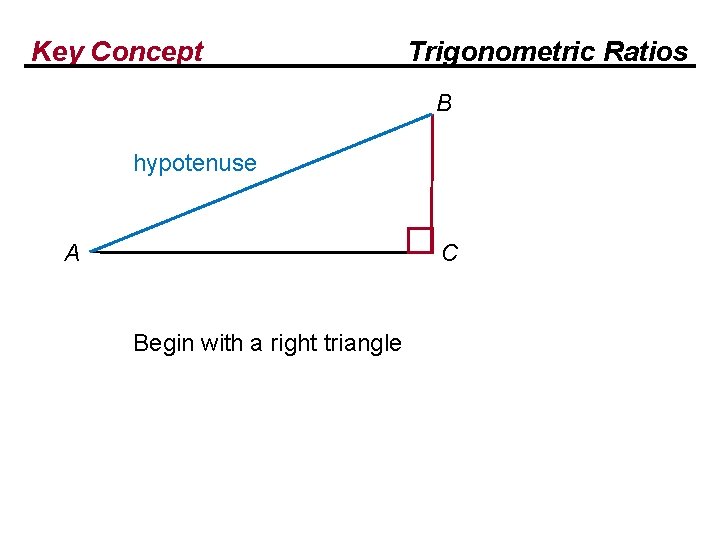
Key Concept Trigonometric Ratios B hypotenuse A C Begin with a right triangle

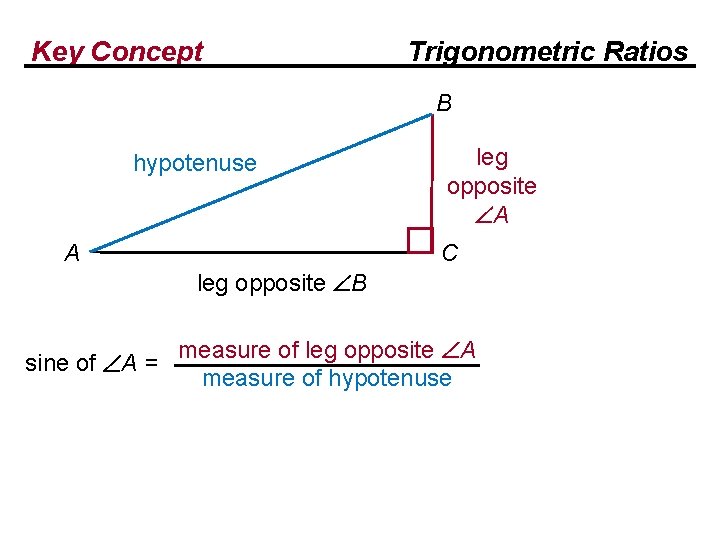
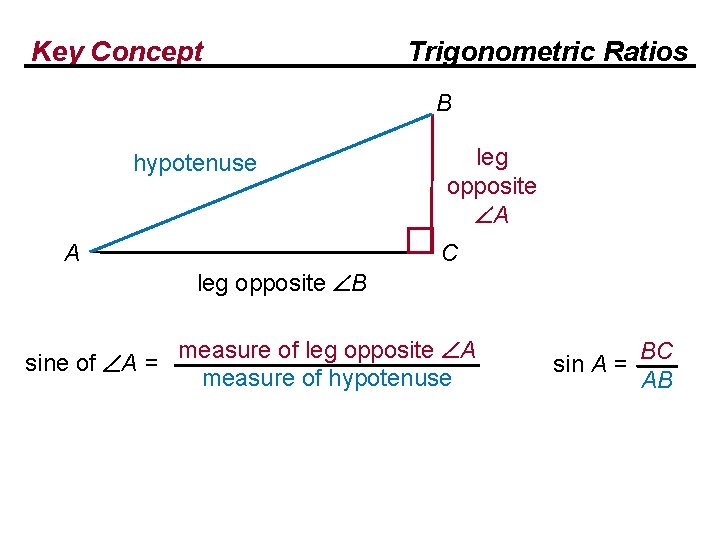
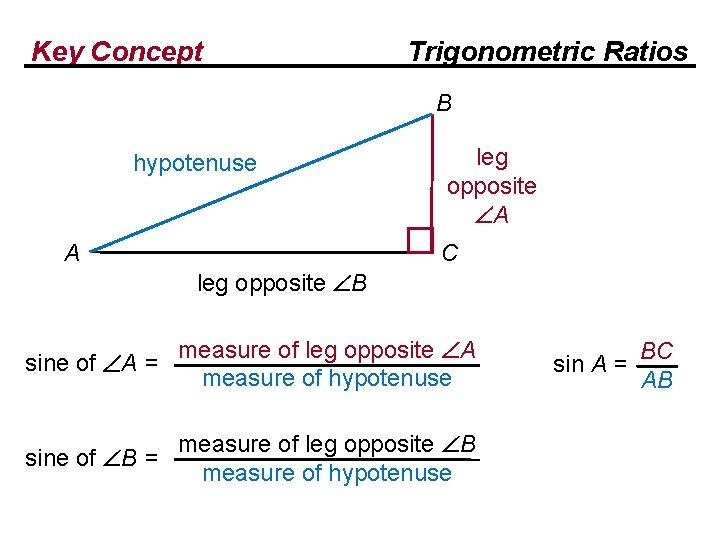
Key Concept Trigonometric Ratios B hypotenuse A leg opposite A C leg opposite B sine of A = measure of leg opposite A measure of hypotenuse

Key Concept Trigonometric Ratios B hypotenuse A leg opposite A C leg opposite B sine of A = measure of leg opposite A measure of hypotenuse BC sin A = AB

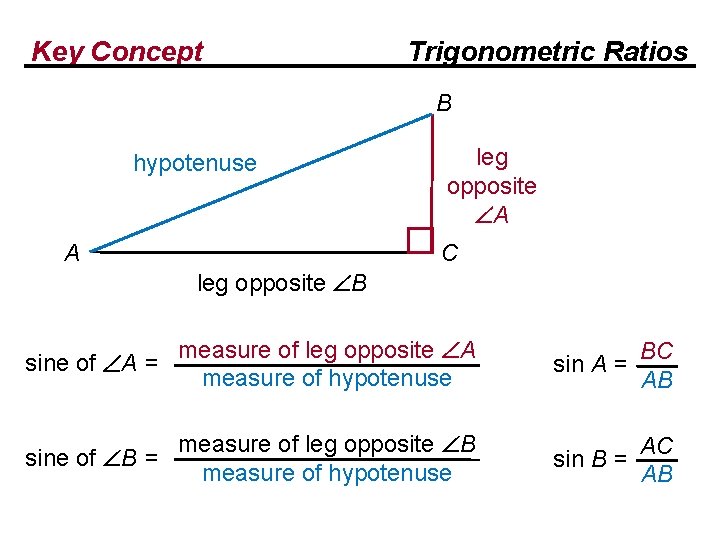
Key Concept Trigonometric Ratios B hypotenuse A leg opposite A C leg opposite B sine of A = measure of leg opposite A measure of hypotenuse measure of leg opposite B sine of B = measure of hypotenuse BC sin A = AB

Key Concept Trigonometric Ratios B hypotenuse A leg opposite A C leg opposite B sine of A = measure of leg opposite A measure of hypotenuse measure of leg opposite B sine of B = measure of hypotenuse BC sin A = AB sin B = AC AB

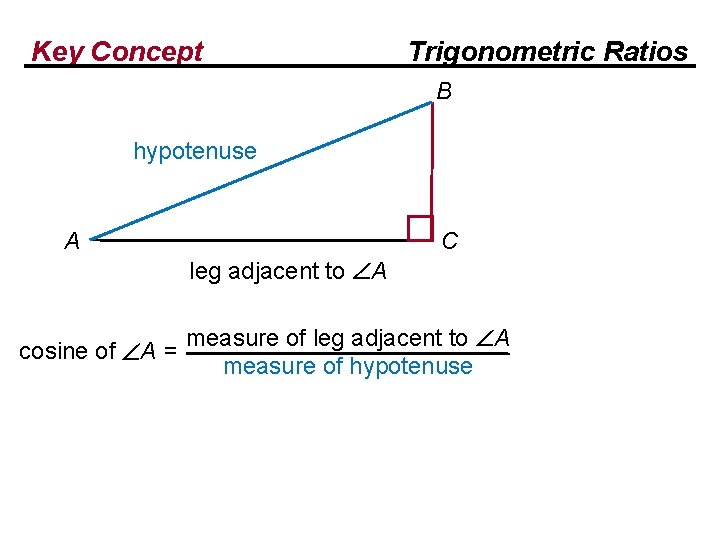
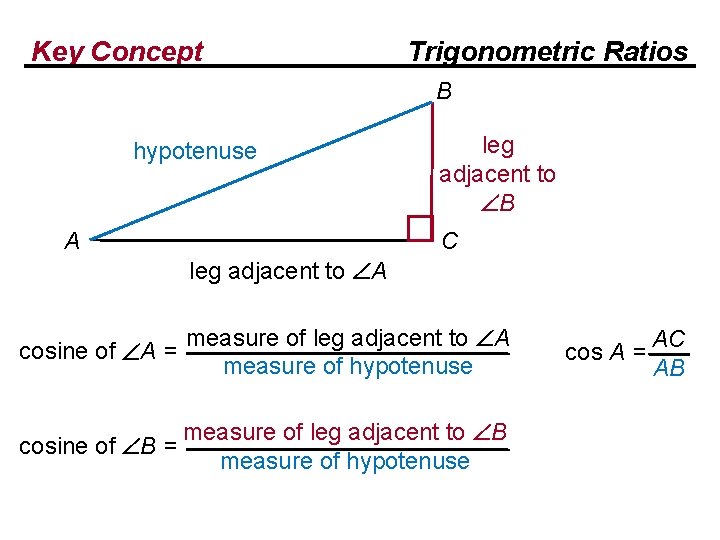
Key Concept Trigonometric Ratios B hypotenuse A C leg adjacent to A cosine of A = measure of leg adjacent to A measure of hypotenuse

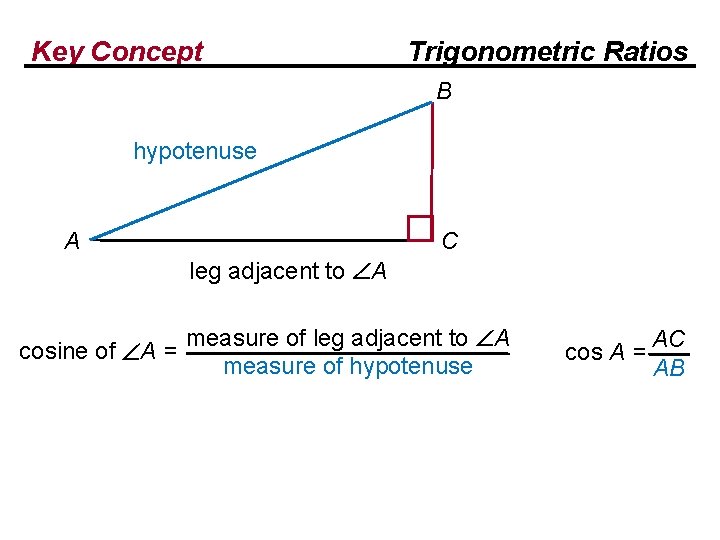
Key Concept Trigonometric Ratios B hypotenuse A C leg adjacent to A cosine of A = measure of leg adjacent to A measure of hypotenuse AC cos A = AB

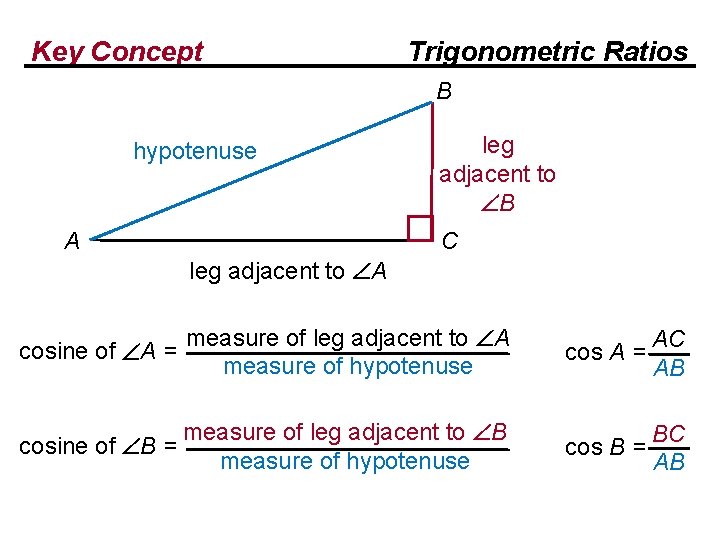
Key Concept Trigonometric Ratios B hypotenuse A leg adjacent to B C leg adjacent to A cosine of A = measure of leg adjacent to A measure of hypotenuse measure of leg adjacent to B cosine of B = measure of hypotenuse AC cos A = AB

Key Concept Trigonometric Ratios B hypotenuse A leg adjacent to B C leg adjacent to A cosine of A = measure of leg adjacent to A measure of hypotenuse measure of leg adjacent to B cosine of B = measure of hypotenuse AC cos A = AB cos B = BC AB

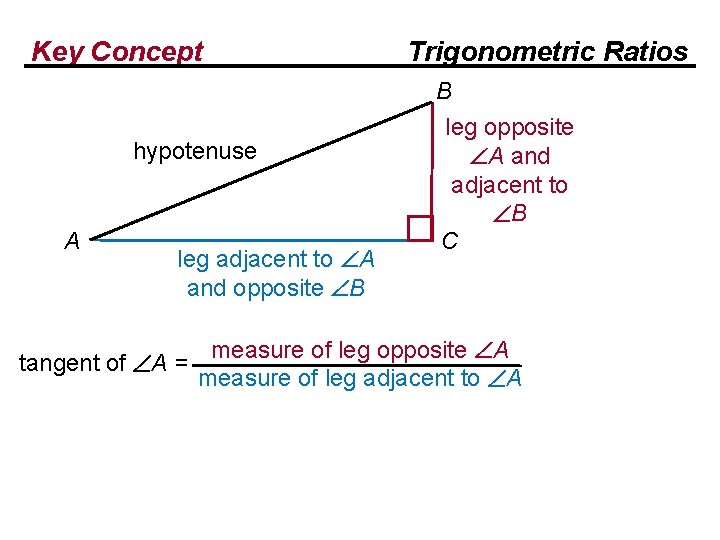
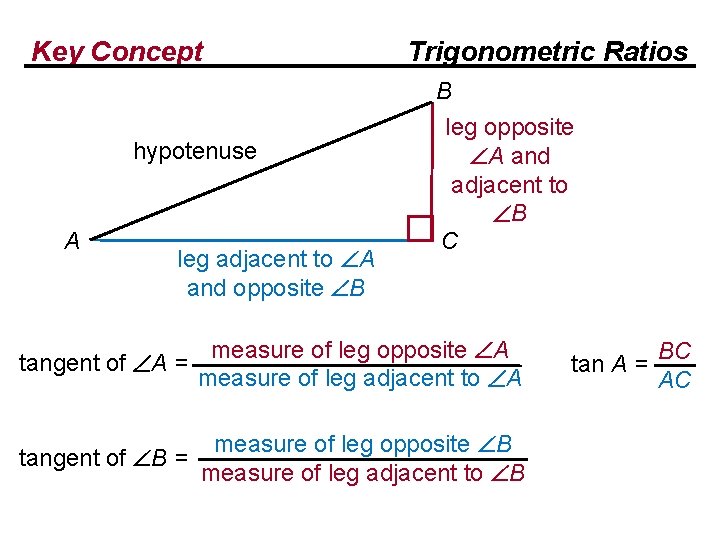
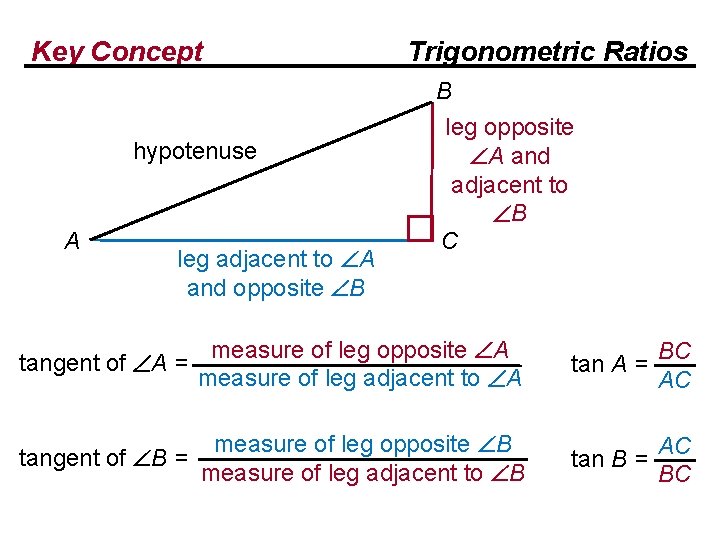
Key Concept hypotenuse A leg adjacent to A and opposite B tangent of A = Trigonometric Ratios B leg opposite A and adjacent to B C measure of leg opposite A measure of leg adjacent to A

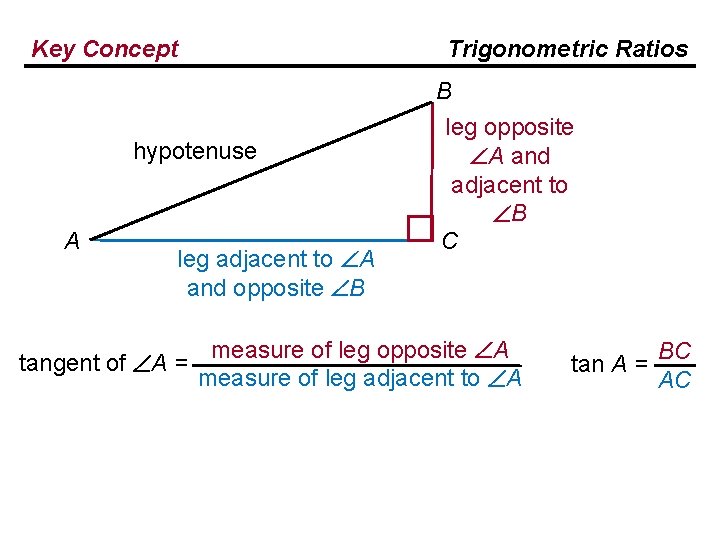
Key Concept Trigonometric Ratios hypotenuse A leg adjacent to A and opposite B tangent of A = B leg opposite A and adjacent to B C measure of leg opposite A measure of leg adjacent to A BC tan A = AC

Key Concept hypotenuse A leg adjacent to A and opposite B tangent of A = Trigonometric Ratios B leg opposite A and adjacent to B C measure of leg opposite A measure of leg adjacent to A measure of leg opposite B tangent of B = measure of leg adjacent to B BC tan A = AC

Key Concept hypotenuse A leg adjacent to A and opposite B tangent of A = Trigonometric Ratios B leg opposite A and adjacent to B C measure of leg opposite A measure of leg adjacent to A measure of leg opposite B tangent of B = measure of leg adjacent to B BC tan A = AC tan B = AC BC

Reading Math SOH – CAH – TOA opp sin A = hyp adj cos A = hyp opp tan A = adj

TRIGONOMETRIC RATIOS The three most common trigonometric ratios are: • Sine • Cosine • Tangent Sine function key Tangent function key Cosine function key