Trigonometry Doing Problems Find unknown sides of triangles

Trigonometry • What you have learned • Finding unknown sides in right angled triangles • Problem solving and Angles of Elevation and Depression

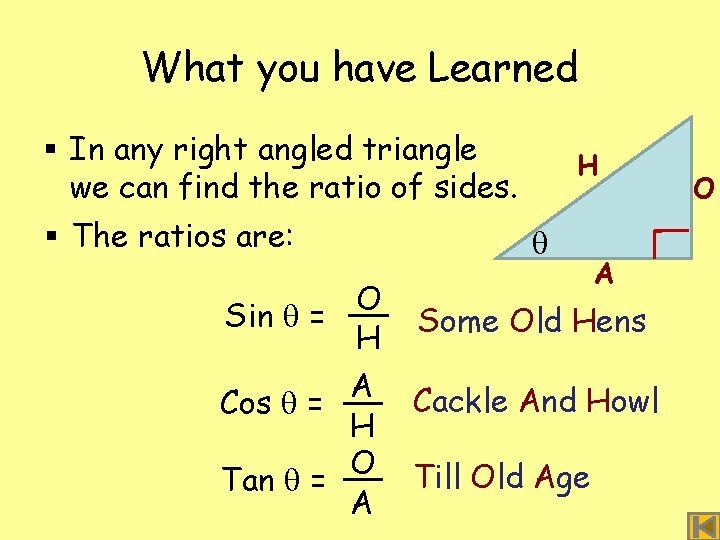
What you have Learned § In any right angled triangle we can find the ratio of sides. § The ratios are: O Sin = H A Cos = H O Tan = A H A Some Old Hens Cackle And Howl Till Old Age O

Find Sides: Example-1 Work only with ABC what angle you know § In triangle A = 25 or want to find. and AB = 7, 8 units. What is 7, 8 length Wethe don’t know of the. BC? adjacent side, leave § Letso. BC = xit out. Ask yourself – we are A 25 working with angle A: B x C Do we know the opposite side to 25 ? Yes - x Do we know the adjacent side to 25 ? No Do we know the hypotenuse? Yes – 7, 8

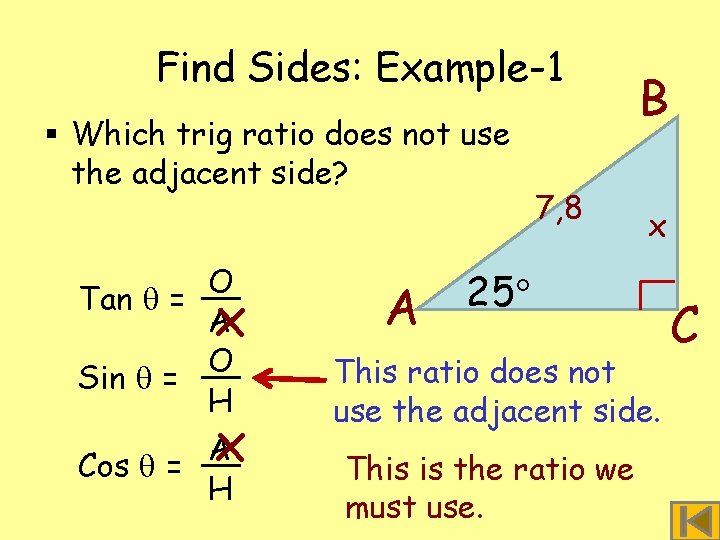
Find Sides: Example-1 § Which trig ratio does not use the adjacent side? O Tan = A O Sin = H x x A Cos = H A 7, 8 B x 25 This ratio does not use the adjacent side. This is the ratio we must use. C

Find Sides: Example-1 § Start with the sine ratio and put in the values. O Sin = H 7, 8 Sin 25 x 7, 8 = 1 7, 8 1 1 7, 8 Sin 25 = x 7, 8 0, 4226 = x A 25 7, 8 B x C To get x on its own multiply both sides by 7, 8. Now simplify. Find sin 25 on calculator. x = 3, 296

Find Sides: Example-2 Work only with PQR what angle you know § In triangle P = 37 or want to find. and PQ = 11, 3 units. What is 11, 3 length Wethe don’t know of the. PR? opposite side, leave § Letso. PR = xit out. 37 x Ask yourself – we are P working with angle P: Q R Do we know the opposite side to 37 ? No Do we know the adjacent side to 37 ? Yes - x Do we know the hypotenuse? Yes – 11, 3

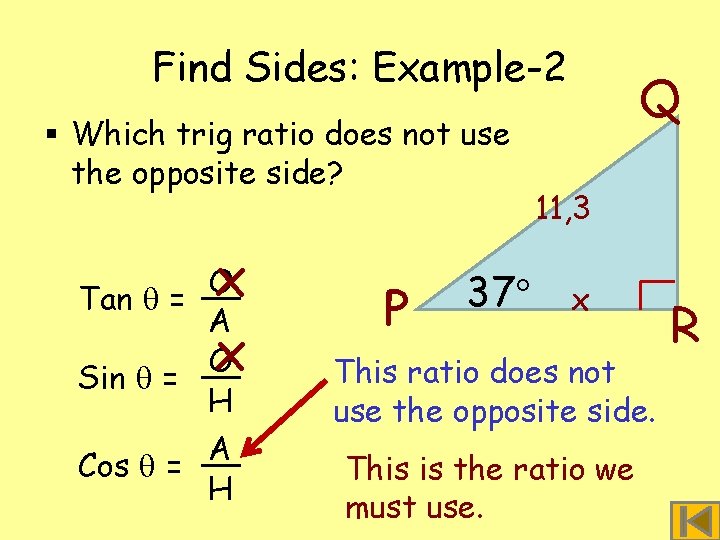
Find Sides: Example-2 § Which trig ratio does not use the opposite side? x x O Tan = A O Sin = H A Cos = H P 37 Q 11, 3 x This ratio does not use the opposite side. This is the ratio we must use. R

Find Sides: Example-2 § Start with the cosine ratio and put in the values. A cos = H 11, 3 cos 37 x 11, 3 = 1 11, 3 1 1 11, 3 cos 37 = x 11, 3 0, 7986 = x P 37 Q 11, 3 x R To get x on its own multiply both sides by 11, 3. Now simplify. Find cos 37 on calculator. x = 9, 024

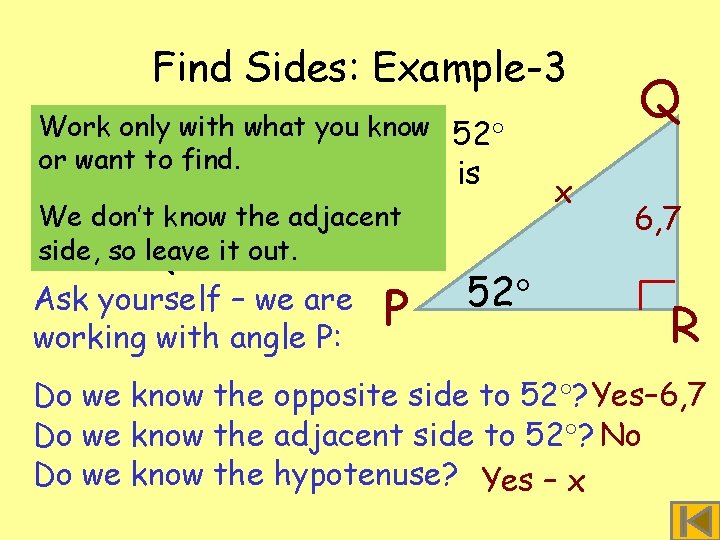
Find Sides: Example-3 Work only with PQR what angle you know § In triangle P = 52 or want to find. and QR = 6, 7 units. What is x length Wethe don’t know of the. PQ? adjacent side, leave § Letso. PQ = xit out. 52 Ask yourself – we are P working with angle P: Q 6, 7 R Do we know the opposite side to 52 ? Yes– 6, 7 Do we know the adjacent side to 52 ? No Do we know the hypotenuse? Yes – x

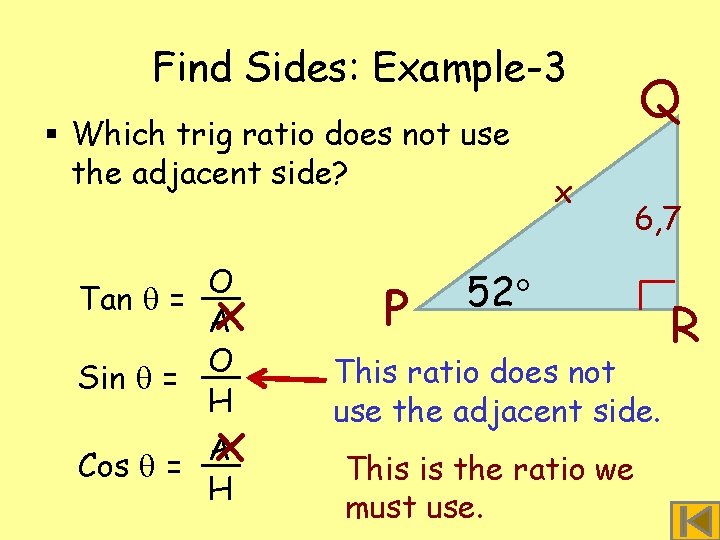
Find Sides: Example-3 § Which trig ratio does not use the adjacent side? O Tan = A O Sin = H x x A Cos = H P x Q 6, 7 52 This ratio does not use the adjacent side. This is the ratio we must use. R

Find Sides: Example-3 § Start with the sine ratio and put in the values. sin = x 1 x O H P sin 52 6, 7 x = 1 x 1 sin 52 = 6, 7 sin 52 x = 6, 7 sin 52 0, 788 x 52 Q 6, 7 R To get x on its own on top multiply both sides by x. Cancel the x’s. Divide both sides by sin 52. Simplify and find sin 52. x = 8, 502

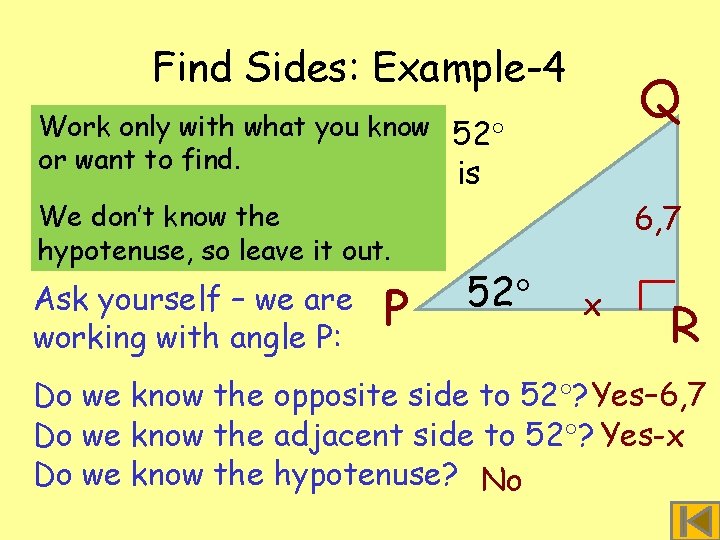
Find Sides: Example-4 Q Work only with PQR what angle you know § In triangle P = 52 or want to find. and QR = 6, 7 units. What is length Wethe don’t know of the. PR? hypotenuse, § Let PR = so x leave it out. 52 Ask yourself – we are P working with angle P: 6, 7 x R Do we know the opposite side to 52 ? Yes– 6, 7 Do we know the adjacent side to 52 ? Yes-x Do we know the hypotenuse? No

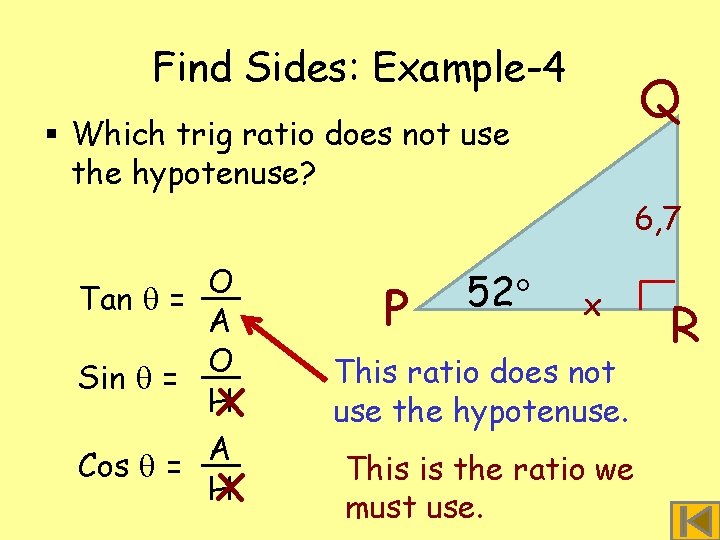
Find Sides: Example-4 Q § Which trig ratio does not use the hypotenuse? 6, 7 O Tan = A O Sin = H P 52 x x This ratio does not use the hypotenuse. x This is the ratio we must use. A Cos = H R

Q Find Sides: Example-4 § Start with the tan ratio and put in the values. O tan = A x 1 x P tan 52 6, 7 x = 1 x 1 tan 52 = 6, 7 tan 52 x = 6, 7 tan 52 1, 279 52 6, 7 x R To get x on its own on top multiply both sides by x. Cancel the x’s. Divide both sides by tan 52. Simplify and find tan 52. x = 5, 238

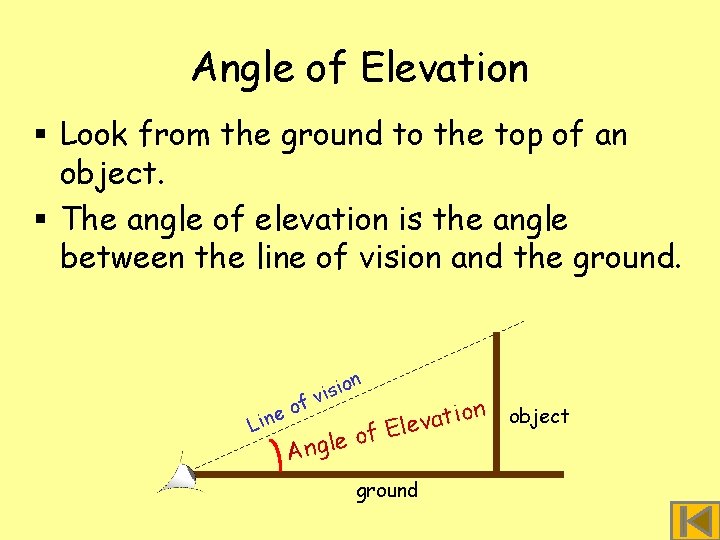
Angle of Elevation § Look from the ground to the top of an object. § The angle of elevation is the angle between the line of vision and the ground. L o e n i f n io s i v n object tio a v e l E f o e l Ang ground

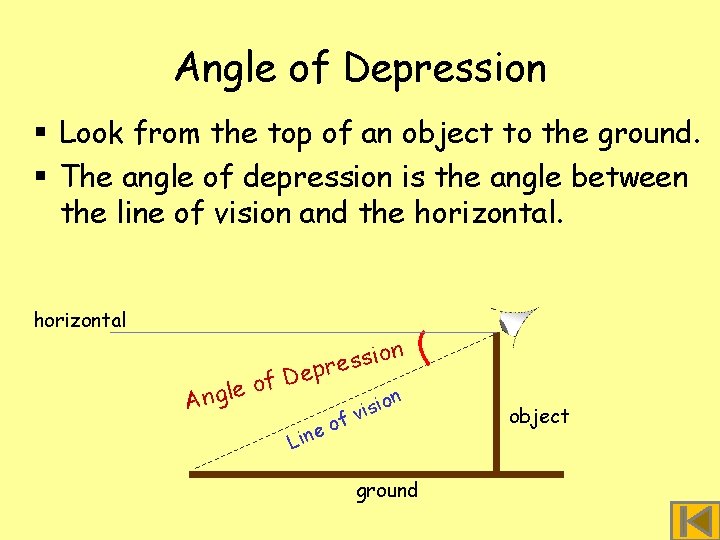
Angle of Depression § Look from the top of an object to the ground. § The angle of depression is the angle between the line of vision and the horizontal De f o Angle n o i s s pre Lin f eo io vis n ground object

A Typical Problem § You have to find the height of a tree. § From where you stand, 76 metres from the tree, the angle to the top of the tree is 32. Always draw a diagram. You don’t have to draw a work of art, just a simple sketch. o ine L 32 f ht g i s Tree Ground

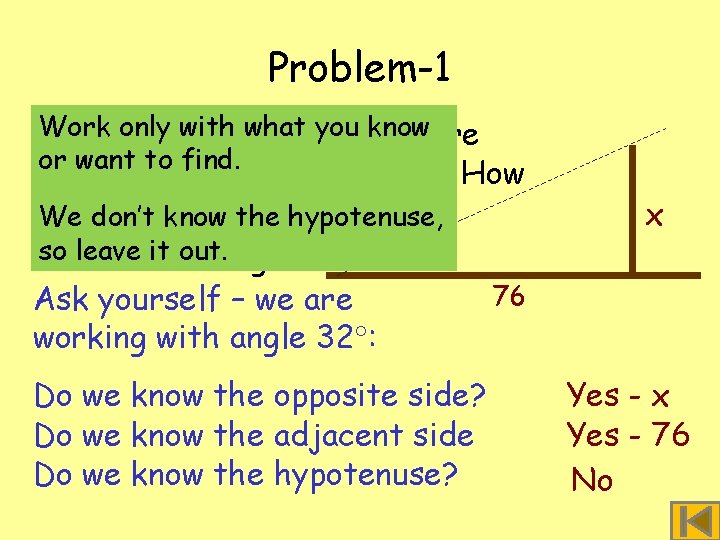
Problem-1 Work withiswhat § Theonly angle 32 you andknow we are or want to find. 76 metres from the tree. How the tree? Wehigh don’tisknow hypotenuse, so leavetree it out. § Let height = x 32 76 Ask yourself – we are working with angle 32 : Do we know the opposite side? Do we know the adjacent side Do we know the hypotenuse? x Yes - 76 No

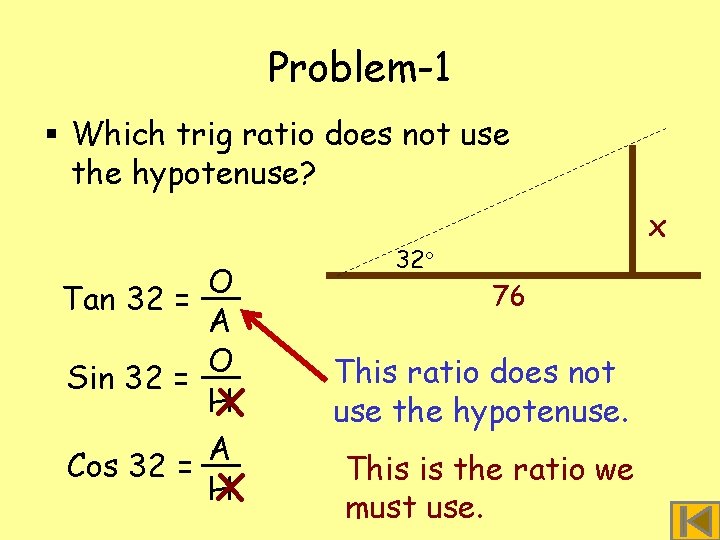
Problem-1 § Which trig ratio does not use the hypotenuse? O Tan 32 = A O Sin 32 = H x 32 76 x This ratio does not use the hypotenuse. x This is the ratio we must use. A Cos 32 = H

Problem-1 § Start with the tan ratio and put in the values. O Tan 32 = A x 32 76 76 1 76 Tan 32 x = 76 1 Tan 32 = x 76 0, 6248 = x 76 1 To get x on its own multiply both sides by 76. Now simplify. Find tan 32 on calculator. x = 4, 873

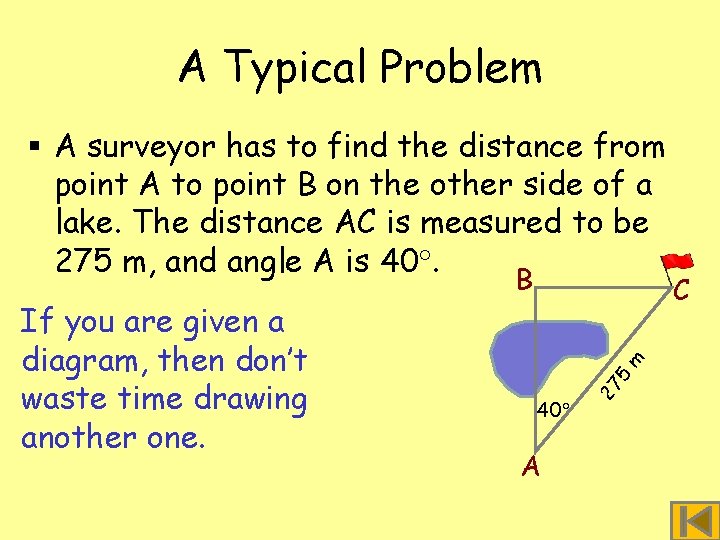
A Typical Problem § A surveyor has to find the distance from point A to point B on the other side of a lake. The distance AC is measured to be 275 m, and angle A is 40. 5 40 A 27 If you are given a diagram, then don’t waste time drawing another one. m B C

Problem 2 C x m 40 and AC = 275 m. What the know length AB? Weisdon’t theofopposite side, leave § Letso. AB = xit out. Ask yourself – we are working with angle A: B 40 27 5 Work only with ABC what angle you know § In triangle A is or want to find. A Do we know the opposite side to 40 ? No Do we know the adjacent side to 40 ? Yes-x Do we know the hypotenuse? Yes - 275

Problem 2 x A Cos = H C x m x O Tan = A O Sin = H B 40 27 5 § Which trig ratio does not use the opposite side? A This ratio does not use the opposite side. This is the ratio we must use.

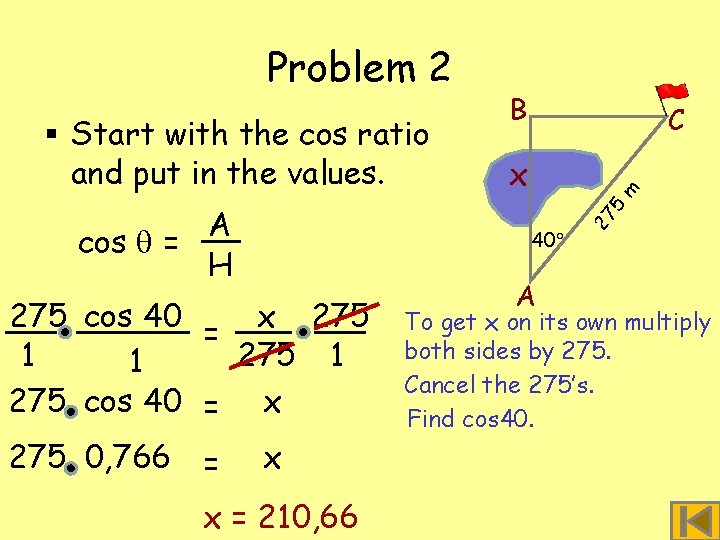
§ Start with the cos ratio and put in the values. = x x x = 210, 66 A 27 40 275 cos 40 x 275 = 1 275 1 1 275 cos 40 = x 275 0, 766 C 5 A cos = H B m Problem 2 To get x on its own multiply both sides by 275. Cancel the 275’s. Find cos 40.

Well Done!

Oops! Click to try again.