TRIGONOMETRY CHAPTER 2 TRIGONOMETRY What is it and

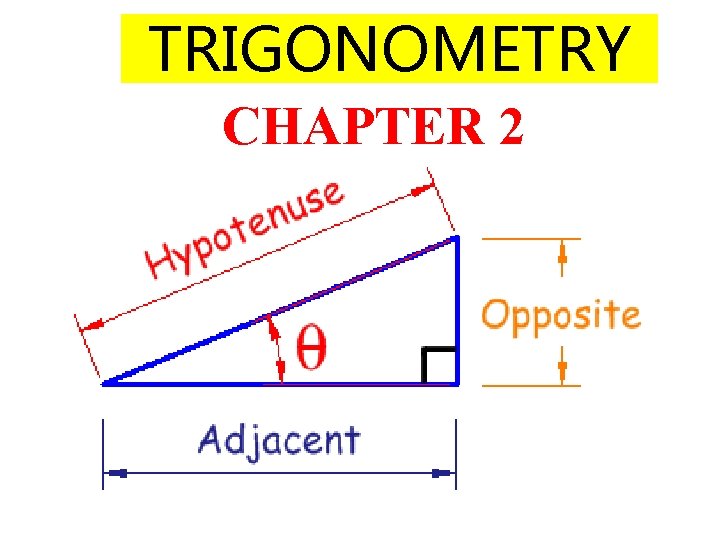
TRIGONOMETRY CHAPTER 2

TRIGONOMETRY What is it and what do we use it for? Trigonometry is a branch of mathematics that studies relationships involving lengths and angles of triangles.

What is it and what do we use it for? Trigonometry is commonly used in finding the height of towers and mountains. It is used in navigation to find the distance of the shore from a point in the sea It is used in oceanography in calculating the height of tides in oceans It is used in finding the distance between celestial bodies

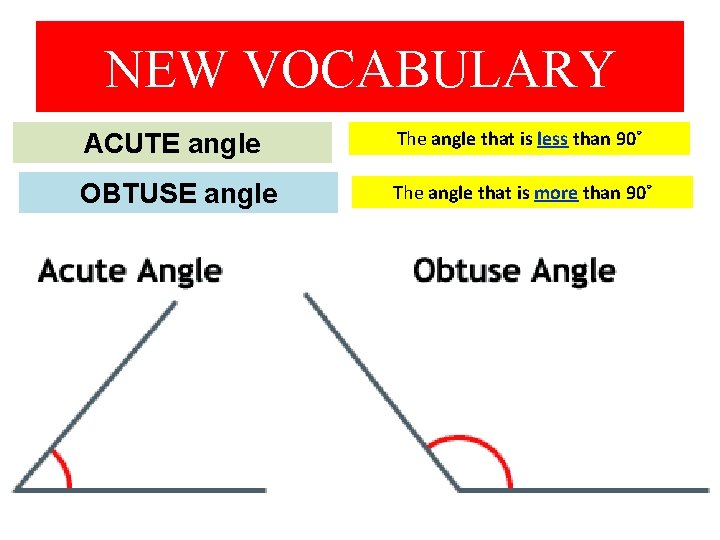
NEW VOCABULARY ACUTE angle The angle that is less than 90˚ OBTUSE angle The angle that is more than 90˚

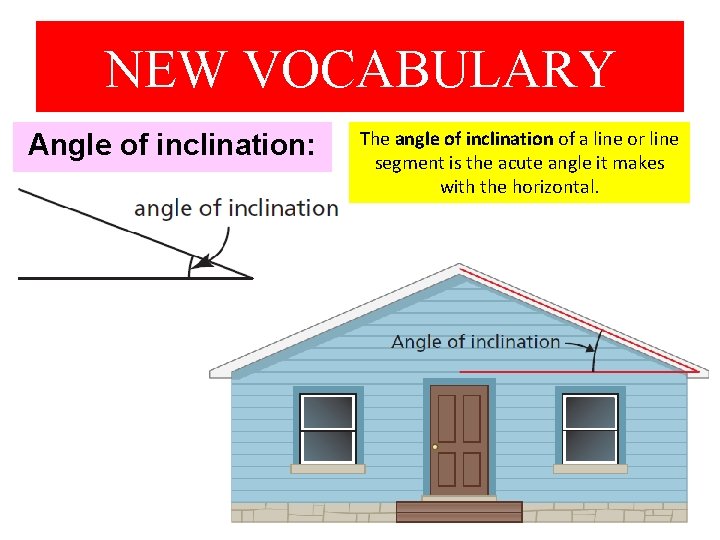
NEW VOCABULARY Angle of inclination: The angle of inclination of a line or line segment is the acute angle it makes with the horizontal.

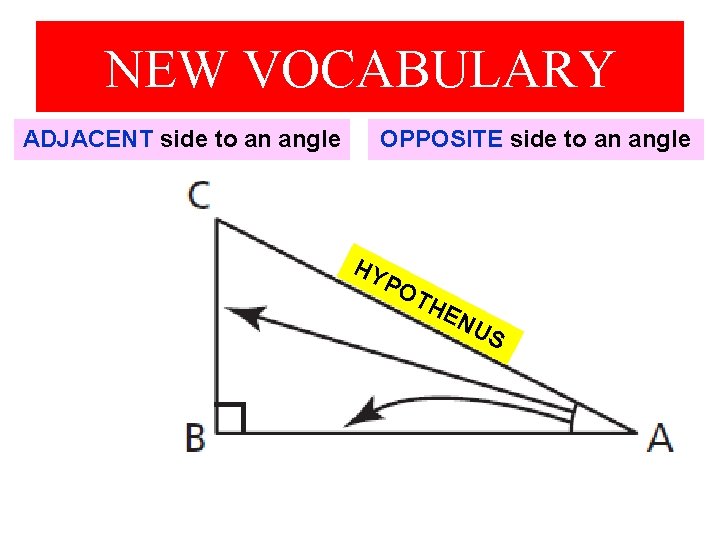
NEW VOCABULARY ADJACENT side to an angle OPPOSITE side to an angle HY PO TH EN US

Construct Understanding • Work with a partner. • You will need grid paper, a ruler, and a protractor. A. On grid paper, draw a right ∆ABC with ∠B = 90°. B. Each of you, draw a different right triangle that is similar to ∆ABC. (What are similar triangles? ) C. Measure the sides and angles of each triangle and label your diagrams with the measures. D. The two shorter sides of a right triangle are its legs. Calculate the ratio of the legs as a decimal, then the corresponding ratio for each of the similar triangles. E. How do the ratios compare? F. What do you think the value of each ratio depends on?

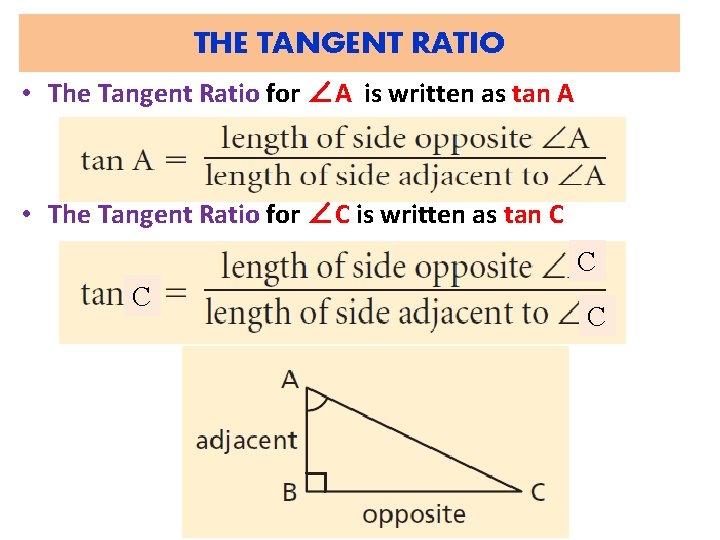
The Ratio of Legs = THE TANGENT RATIO • Length of side opposite ∠A : Length of side adjacent to ∠A • depends only on the measure of the angle, not on how large or small the triangle is. • Usually written as a fraction

THE TANGENT RATIO • The Tangent Ratio for ∠A is written as tan A • The Tangent Ratio for ∠C is written as tan C C

The Value of THE TANGENT RATIO • The value of this ratio is usually expressed as a decimal without a unit For Example: o If tan A = 1. 5, then in any similar triangle with ∠A, the length of side opposite to ∠A is 1. 5 times greater than the length of the side adjacent to ∠A

The Value of THE TANGENT RATIO For Example: o If tan A = 1. 5, then in any similar triangle with ∠A, the length of side opposite to ∠A is 1. 5 times greater than the length of the side adjacent to ∠A

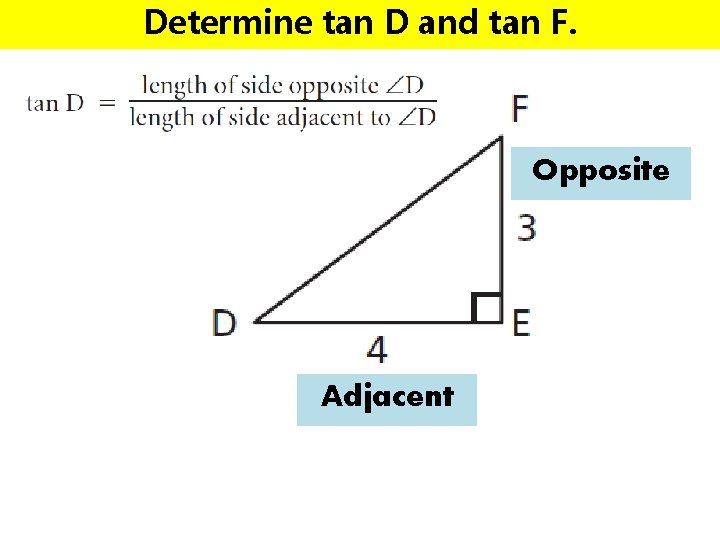
Determine tan D and tan F. Opposite Adjacent

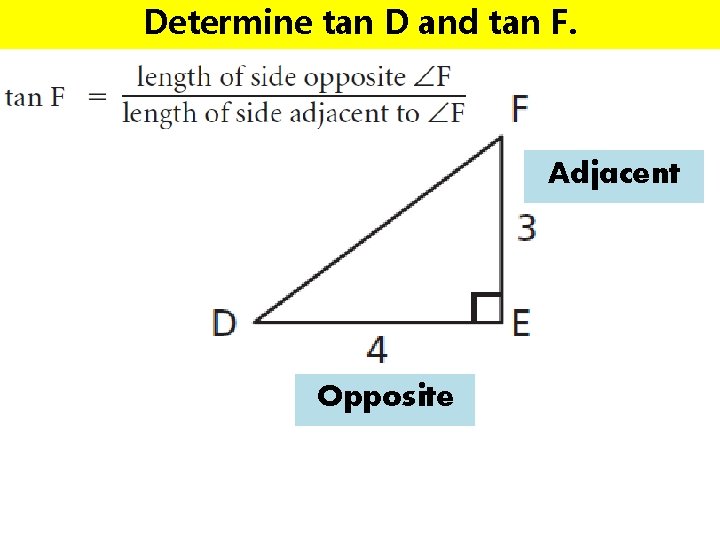
Determine tan D and tan F. Adjacent Opposite

POWERPOINT PRACTICE PROBLEM Determine tan X and tan Z.

The Value of THE TANGENT RATIO • The value of this ratio can also be used to find the value of an acute angle

The Value of THE TANGENT RATIO • The value of this ratio can also be used to find the value of an acute angle DEGREE MODE

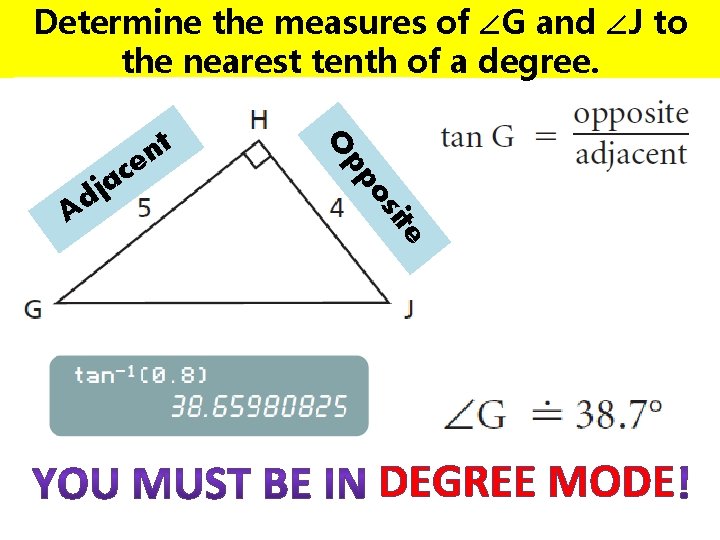
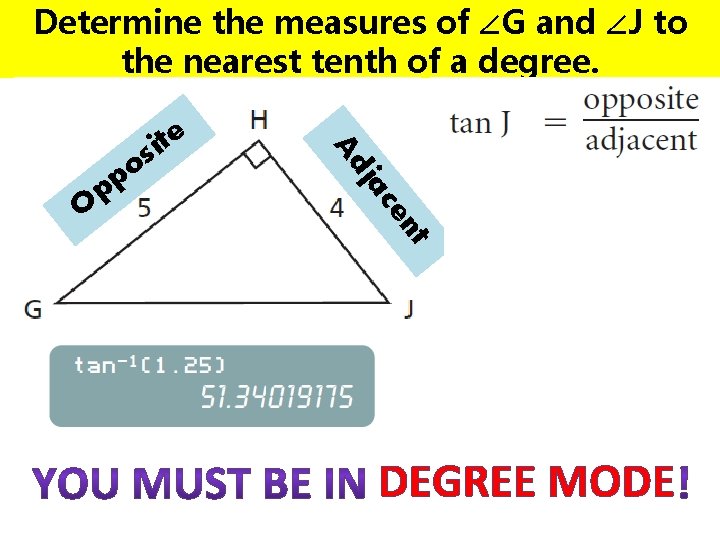
Determine the measures of ∠G and ∠J to the nearest tenth of a degree. os pp O ite A a j d t n ce DEGREE MODE

Determine the measures of ∠G and ∠J to the nearest tenth of a degree. nt ce ja Ad O o p p e t i s DEGREE MODE

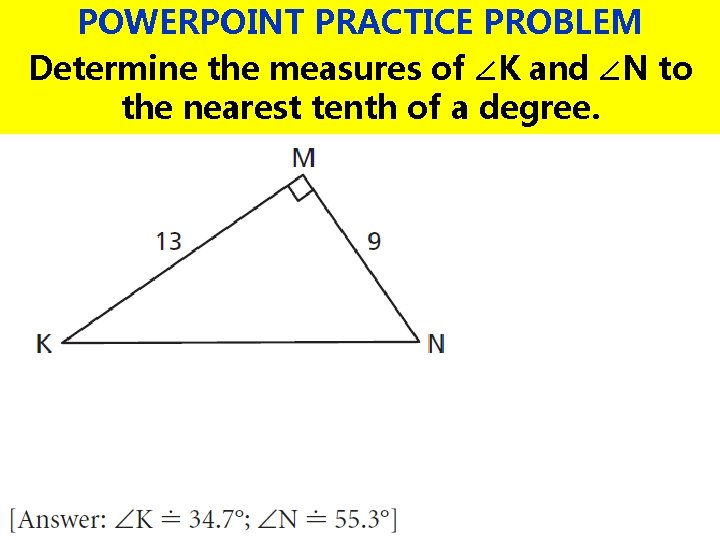
POWERPOINT PRACTICE PROBLEM Determine the measures of ∠K and ∠N to the nearest tenth of a degree.

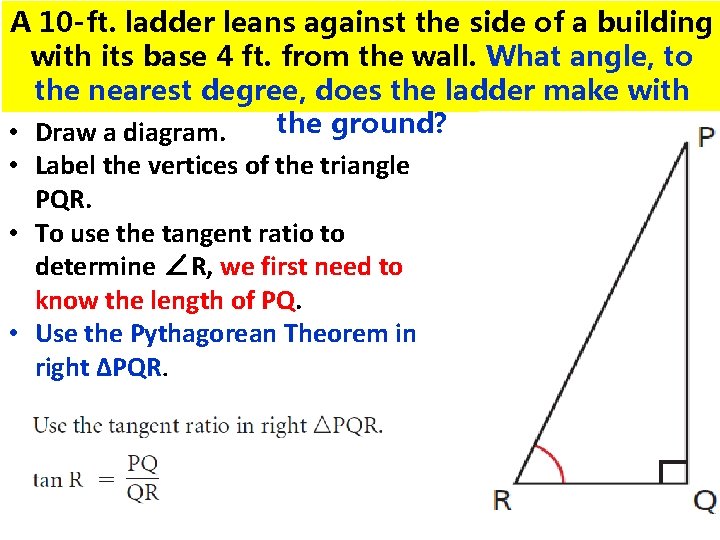
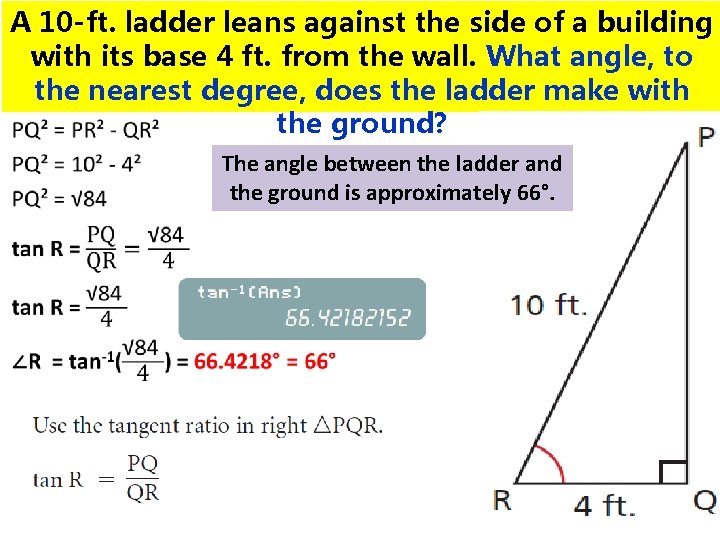
A 10 -ft. ladder leans against the side of a building with its base 4 ft. from the wall. What angle, to the nearest degree, does the ladder make with the ground?

A 10 -ft. ladder leans against the side of a building with its base 4 ft. from the wall. What angle, to the nearest degree, does the ladder make with the ground? • Draw a diagram. • Label the vertices of the triangle PQR. • To use the tangent ratio to determine ∠R, we first need to know the length of PQ. • Use the Pythagorean Theorem in right ∆PQR.

A 10 -ft. ladder leans against the side of a building with its base 4 ft. from the wall. What angle, to the nearest degree, does the ladder make with the ground? The angle between the ladder and the ground is approximately 66°.

HOMEWORK O PAGE: 75 - 77 O PROBLEMS: 3, 4, 5, 12, 17, 20, 21,