Trigonometry Chapter 14 Section 1 Basic Trig Graphs

Trigonometry Chapter 14 Section 1

Basic Trig Graphs If we take the values for sin that we determined from last chapter from x = 0 to x = 2π, we get a graph from these values: Sin of 00 900 1800 2700 3600

Basic Trig Graphs If we take the values for cos that we determined from last chapter from x = 0 to x = 2π, we get a graph from these values: cos of 00 900 1800 2700 3600

Basic Trig Graphs If we take the values for tan that we determined from last chapter from x = 0 to x = 2π, we get a graph from these values: tan of 00 900 1800 2700 3600

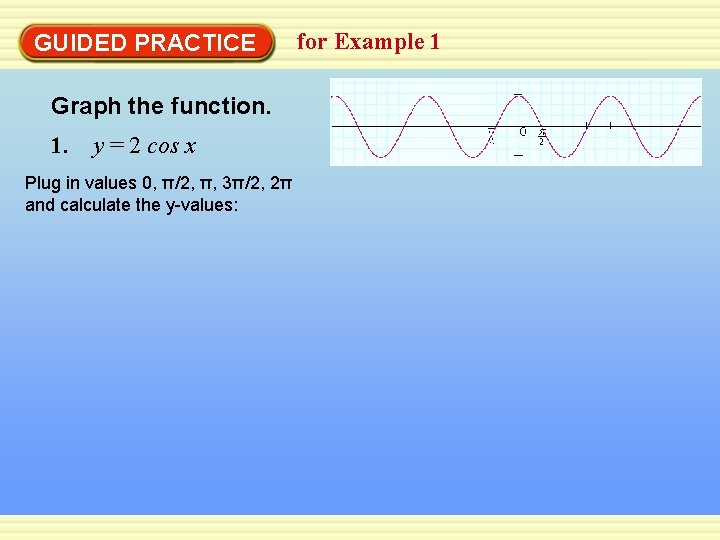
GUIDED PRACTICE Graph the function. 1. y = 2 cos x Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values: for Example 1

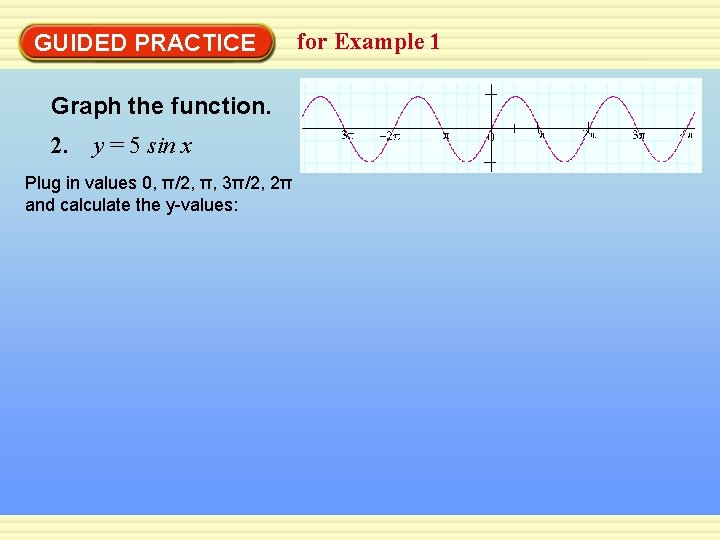
GUIDED PRACTICE Graph the function. 2. y = 5 sin x Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values: for Example 1

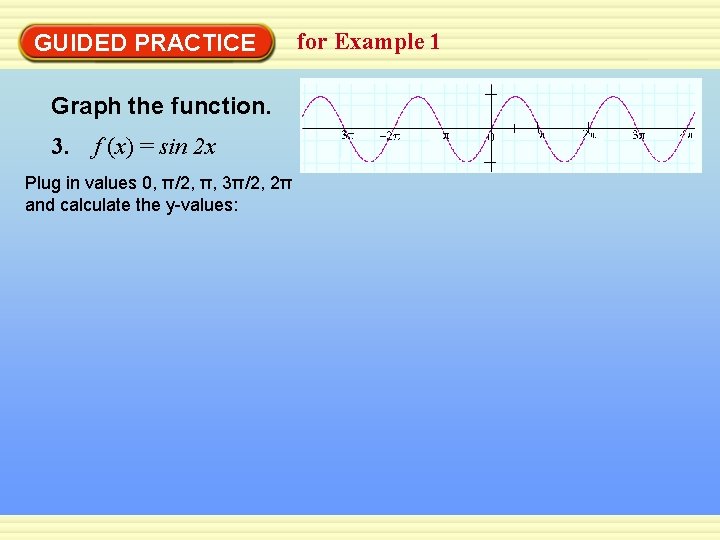
GUIDED PRACTICE Graph the function. 3. f (x) = sin 2 x Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values: for Example 1

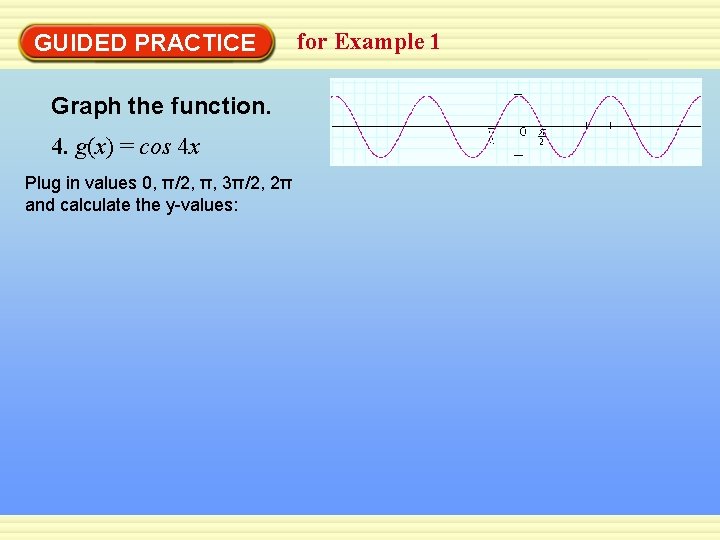
GUIDED PRACTICE Graph the function. 4. g(x) = cos 4 x Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values: for Example 1

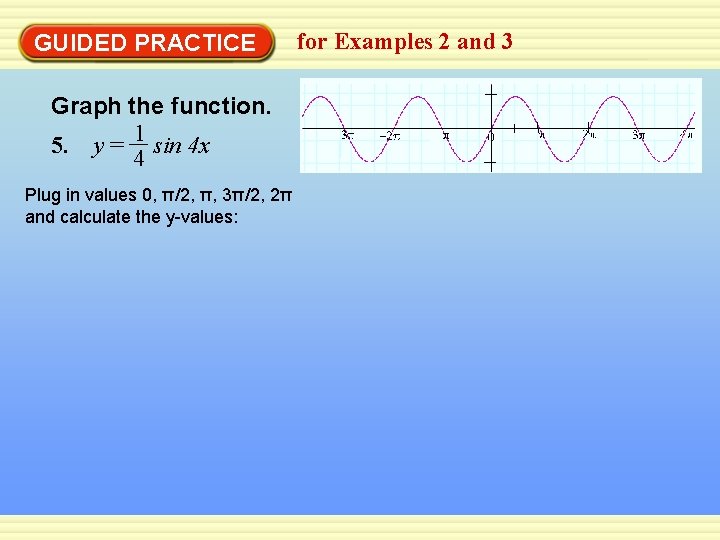
GUIDED PRACTICE Graph the function. 1 5. y = sin 4 x 4 Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values: for Examples 2 and 3

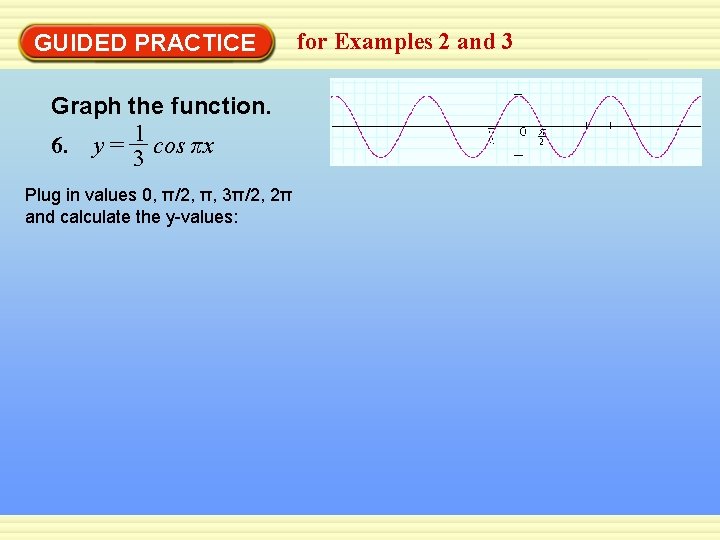
GUIDED PRACTICE Graph the function. 1 6. y = cos πx 3 Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values: for Examples 2 and 3

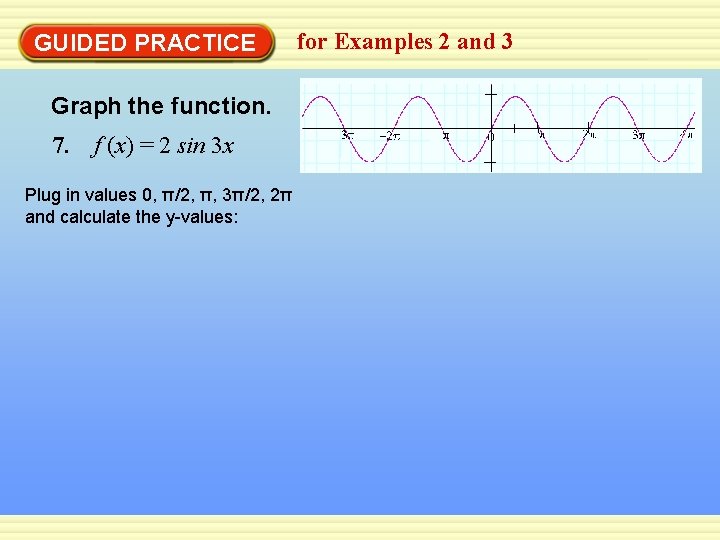
GUIDED PRACTICE Graph the function. 7. f (x) = 2 sin 3 x Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values: for Examples 2 and 3

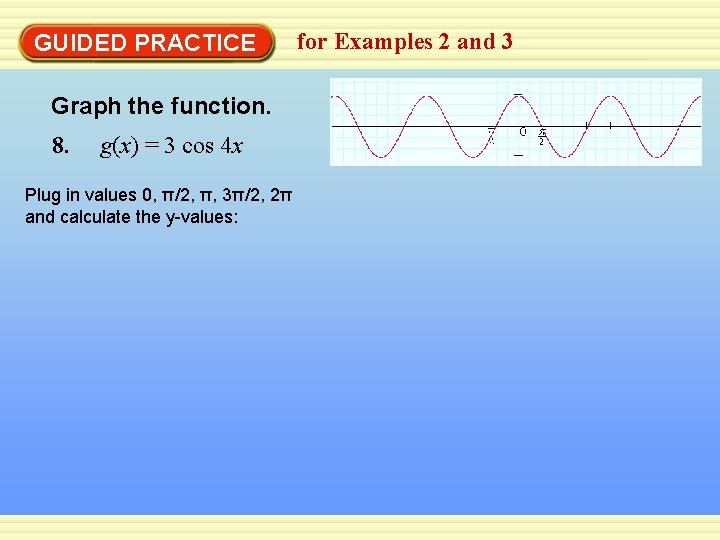
GUIDED PRACTICE Graph the function. 8. g(x) = 3 cos 4 x Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values: for Examples 2 and 3

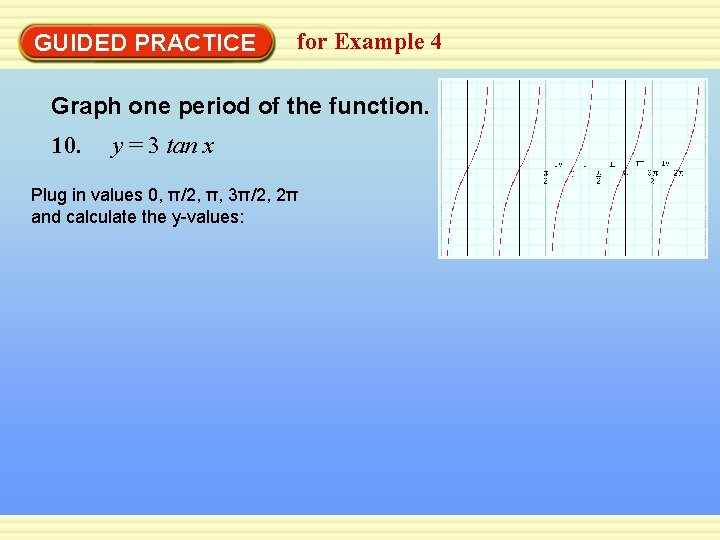
GUIDED PRACTICE for Example 4 Graph one period of the function. 10. y = 3 tan x Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values:

GUIDED PRACTICE for Example 4 Graph one period of the function. 11. y = tan 2 x

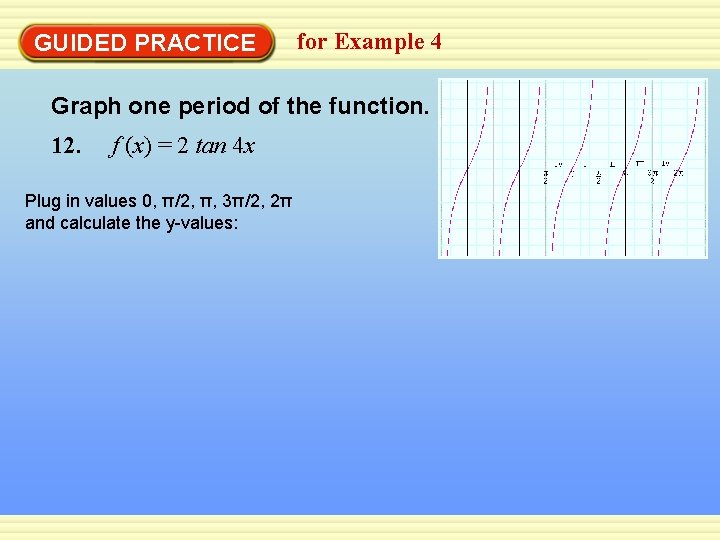
GUIDED PRACTICE for Example 4 Graph one period of the function. 12. f (x) = 2 tan 4 x Plug in values 0, π/2, π, 3π/2, 2π and calculate the y-values:

Trigonometry Chapter 14 Section 2

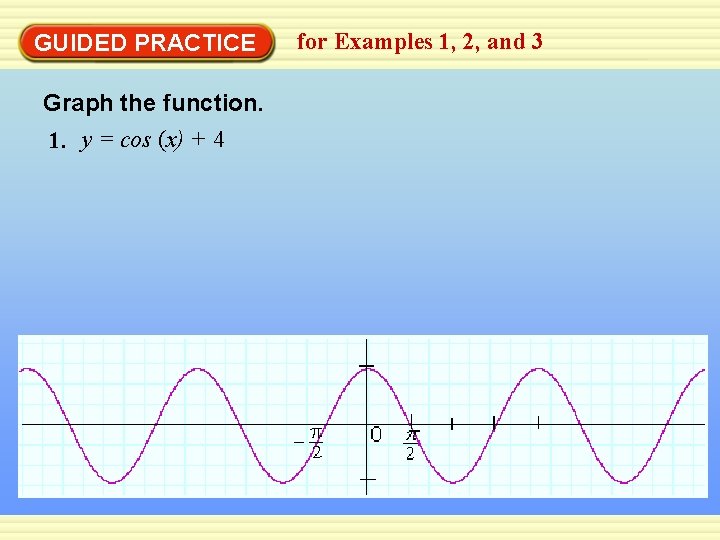
GUIDED PRACTICE Graph the function. 1. y = cos (x) + 4 for Examples 1, 2, and 3

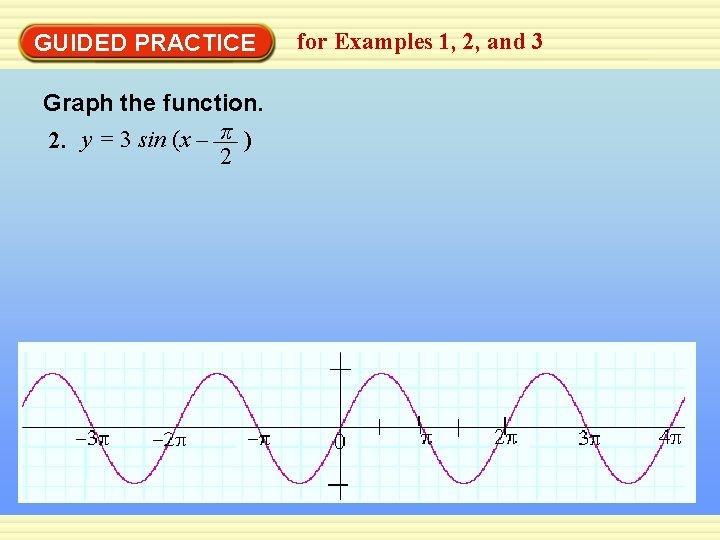
GUIDED PRACTICE Graph the function. 2. y = 3 sin (x – π ) 2 for Examples 1, 2, and 3

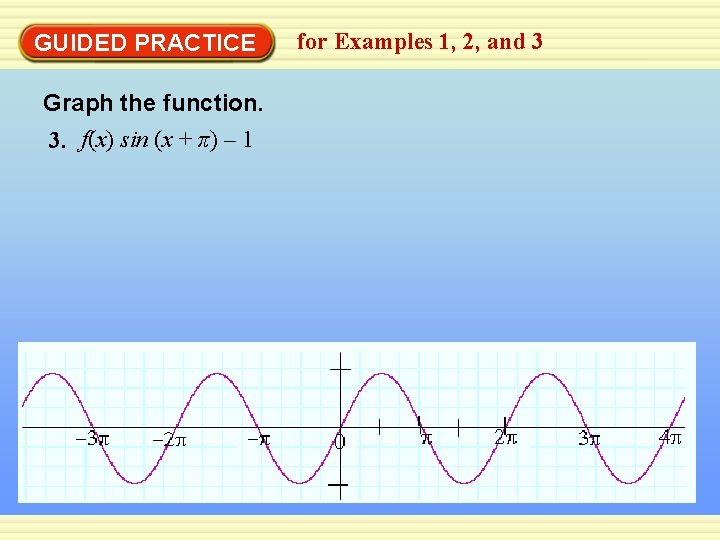
GUIDED PRACTICE Graph the function. 3. f(x) sin (x + π) – 1 for Examples 1, 2, and 3

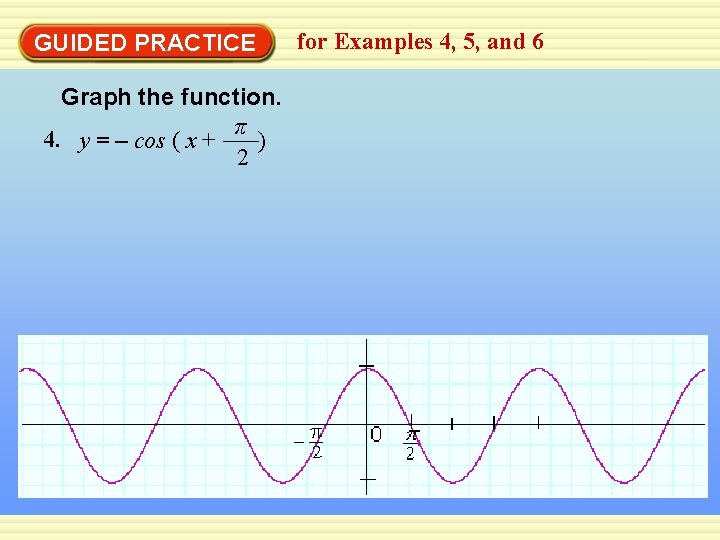
GUIDED PRACTICE Graph the function. π 4. y = – cos ( x + ) 2 for Examples 4, 5, and 6

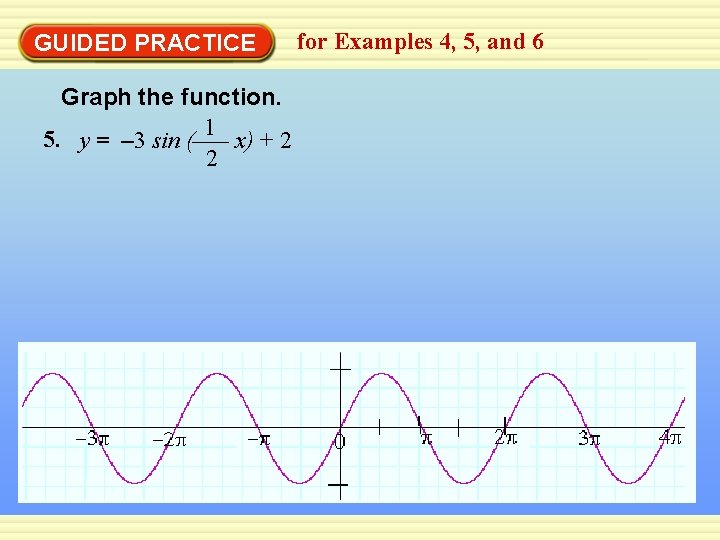
GUIDED PRACTICE Graph the function. 5. y = – 3 sin ( 1 x) + 2 2 for Examples 4, 5, and 6

GUIDED PRACTICE Graph the function. 6. f(x) = – tan (2 x) – 1 for Examples 4, 5, and 6

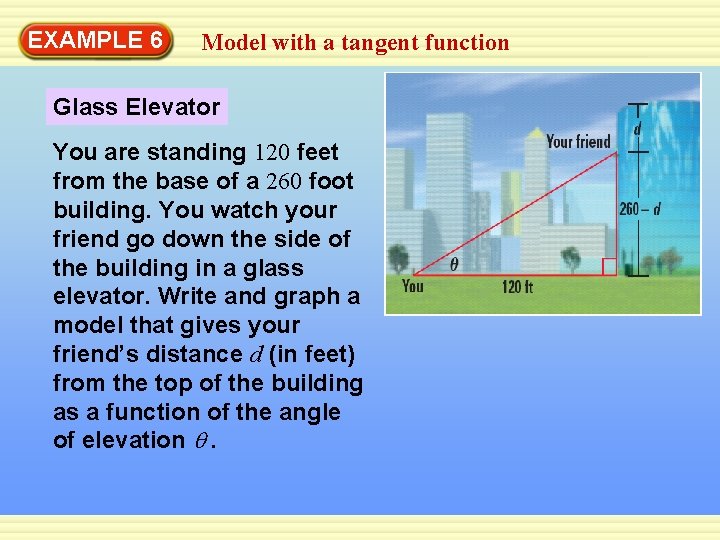
EXAMPLE 6 Model with a tangent function Glass Elevator You are standing 120 feet from the base of a 260 foot building. You watch your friend go down the side of the building in a glass elevator. Write and graph a model that gives your friend’s distance d (in feet) from the top of the building as a function of the angle of elevation q.

GUIDED PRACTICE for Examples 4, 5, and 6 7. What if ? In example 6, how does the model change if you are standing 150 feet from a building that is 400 feet tall ?

Trigonometry Chapter 14 Section 3

GUIDED PRACTICE for Examples 1, 2, and 3 Find the values of the other five trigonometric functions of q. 1. cos q = 1 , 0 < q < π 6 2

GUIDED PRACTICE for Examples 1, 2, and 3 Find the values of the other five trigonometric functions of q. 2. sin q = – 3 , π < q < 3π 7 2

Trig Identities

GUIDED PRACTICE for Examples 1, 2, and 3 Simplify the expression. 3. sin x cot x sec x 4. tan x csc x sec x 5. cos π – q – 1 2 1 + sin (–q )

GUIDED PRACTICE Verify the identity. 6. cot (–q ) = –cot q for Examples 4, 5, and 6

GUIDED PRACTICE for Examples 4, 5, and 6 7. csc 2 x (1 – sin 2 x) = cot 2 x

GUIDED PRACTICE 8. cos x csc x tan x = 1 for Examples 4, 5, and 6

GUIDED PRACTICE for Examples 4, 5, and 6 9. (tan 2 x + 1)(cos 2 x – 1) = – tan 2 x

Trigonometry Chapter 14 Section 4

GUIDED PRACTICE for Examples 1, 2, and 3 1. Find the general solution of the equation 2 sin x + 4 = 5.

GUIDED PRACTICE for Examples 1, 2, and 3 2. Solve the equation 3 csc 2 x = 4 in the interval 0 ≤ x <2π.

EXAMPLE 3 Oceanography Solve a real-life trigonometric equation The water depth d for the Bay of Fundy can be modeled by d = 35 – 28 cos π t 6. 2 where d is measured in feet and t is the time in hours. If t = 0 represents midnight, at what time(s) is the water depth 63 feet?

GUIDED PRACTICE for Examples 4, 5, and 6 Find the general solution of the equation. 4. sin 3 x – sin x = 0 5. 1 – cos x = 3 sin x

GUIDED PRACTICE for Examples 4, 5, and 6 Solve the equation in the interval 0 ≤ x <π. 6. 2 sin x = csc x 7. tan 2 x – sin x tan 2 x = 0

Trigonometry Chapter 14 Section 6

GUIDED PRACTICE for Examples 1 and 2 Find the exact value of the expression. 1. sin 105° 2. cos 75° 3. tan 5π 12 4. cos π 12

GUIDED PRACTICE 5. for Examples 1 and 2 π 8 Find sin (a – b) given that sin a = 17 with 0 < a < 2 3π and cos b = – 24 with π < b <. 2 25

GUIDED PRACTICE for Examples 3, 4, and 5 Simplify the expression. 6. sin (x + 2π) 7. cos (x – 2π) 8. tan (x – π)

GUIDED PRACTICE for Examples 3, 4, and 5 9. Solve 6 cos ( π t ) + 5 = – 24 sin ( π t + 22) + 5 for 0 ≤ t < 2π. 75 75

Trigonometry Chapter 14 Section 7

GUIDED PRACTICE for Examples 1, 2, and 3 Find the exact value of the expression. 1. tan π 8 2. sin 5π 8 3. cos 15°

GUIDED PRACTICE for Examples 1, 2, and 3 Find the exact value of the expression. a 4. Given sin a = 2 with 0 < a < π , find cos 2 a and tan. 2 2 2 5. Given cos a = – 3π 3 with π < a < , find sin 2 a and sin a. 2 5 2

GUIDED PRACTICE for Examples 1, 2, and 3 Simplify the expression. cos 2 q 6. sin q + cos q 7. tan 2 x tan x

GUIDED PRACTICE for Examples 5, 6, and 7 Solve the equation. 13. tan 2 x + tan x = 0 for 0 ≤ x <2π.

GUIDED PRACTICE Solve the equation. 14. 2 cos x + 1 = 0 2 for Examples 5, 6, and 7

GUIDED PRACTICE for Examples 5, 6, and 7 Verify the identity. 11. sin 3 x = 3 sin x – 4 sin 3 x SOLUTION

GUIDED PRACTICE for Examples 5, 6, and 7 Verify the identity. 12. 1 + cos 10 x = 2 cos 2 5 x