Trigonometry By Oscar Lopez Unit 1 Angles Degrees

Trigonometry By Oscar Lopez

Unit 1: Angles & Degrees Examples of Conversion An angle is an opening which is measured using degrees. Radians are the measurement where the radius and the arc length are equal to each other. When converting degrees to radians you multiply Pi over 180 degrees to find the measurement. When converting radians to degrees the 180 degrees switches and is placed over Pi.

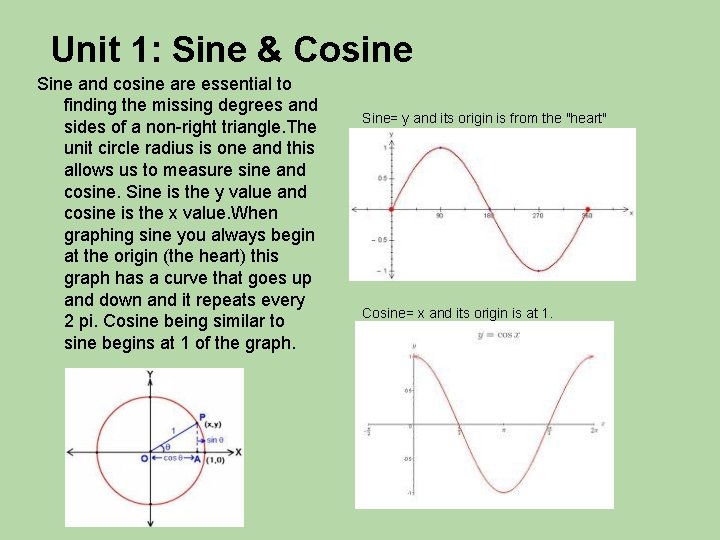
Unit 1: Sine & Cosine Sine and cosine are essential to finding the missing degrees and sides of a non-right triangle. The unit circle radius is one and this allows us to measure sine and cosine. Sine is the y value and cosine is the x value. When graphing sine you always begin at the origin (the heart) this graph has a curve that goes up and down and it repeats every 2 pi. Cosine being similar to sine begins at 1 of the graph. Sine= y and its origin is from the "heart" Cosine= x and its origin is at 1.

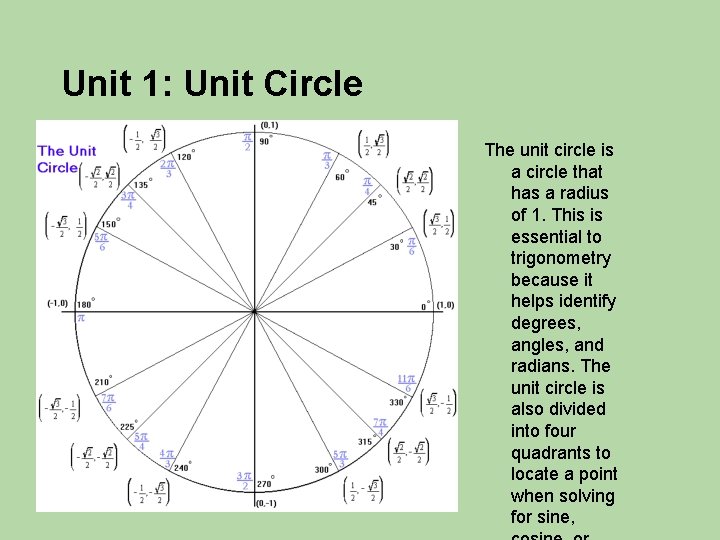
Unit 1: Unit Circle The unit circle is a circle that has a radius of 1. This is essential to trigonometry because it helps identify degrees, angles, and radians. The unit circle is also divided into four quadrants to locate a point when solving for sine,

Unit 2: Basic Trigonometric Functions SOHCAHTOA This a way to remember the basic trigonometric functions sine. cosine, and tangent. These functions are use to solve for missing angles and sides of any triangle.

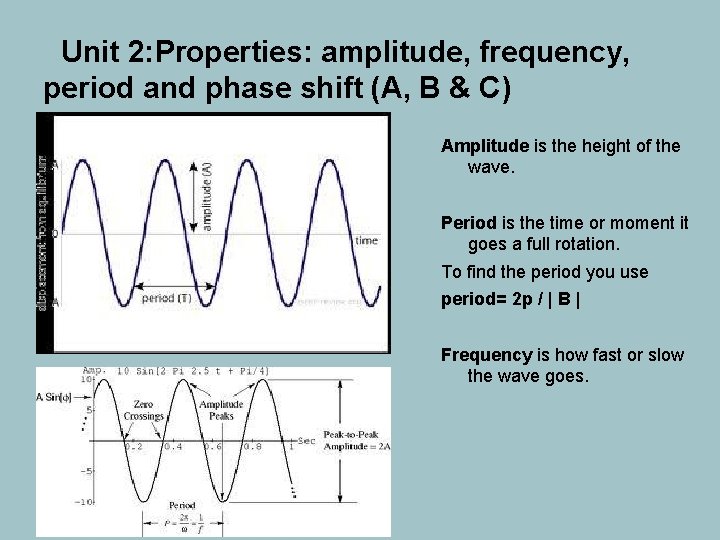
Unit 2: Properties: amplitude, frequency, period and phase shift (A, B & C) Amplitude is the height of the wave. Period is the time or moment it goes a full rotation. To find the period you use period= 2 p / | B | Frequency is how fast or slow the wave goes.

Unit 2: Functions of the form f(t)=A sin (Bt + C) & f(t)=A cos (Bt + C) When graphing f(t)=A sin (Bt + C)A stands for the amplitude B is the period which is 2 pi/ |B|and C is the phase shift. Both sine and cosine graphs have a period of 2 pi ( both make a full wave) f(t)=A cos (Bt + C): When having cosine it is similar to sine except that in this function it is reverse of sine.

Unit 3: Analytical Trigonometry

Applications of Trigonometry (Standard 16. 0) Term Technical Definition Vectors A vector has magnitude (how long it is) and direction. http: //www. mathsisfun. com/algebra/vect ors. html Parametric Equation A curve in the plane is said to be parameterized if the set of coordinates on the curve, (x, y), are represented as functions of a variable t. Namely, x = f(t), y = g(t) t. D. where D is a set of real numbers. The variable t is called a parameter and the relations between x, y and t are called parametric equations. Polar Equations The polar coordinate system consists of a pole and a polar axis. The pole is a fixed point, and the polar axis is a directed ray whose endpoint is the pole. Every point in the plane of the polar axis can be specified according to two coordinates: r , the distance between the point and the pole, and θ , the angle between the polar axis and the ray containing the point whose endpoint is also the pole. Examples https: //www. khanacademy. or g/math/linearalgebra/vectors_and_spaces /vectors/v/linear-algebra-- http: //colalg. math. csusb. ed u/~devel/precalcdemo/para m/src/param. html http: //www. sparknotes. com /math/precalc/parametrice quationsandpolarcoordinat es/section 2. rhtml

Applications of Trigonometry (Standard 16. 0) Summary/ Observation s A vector is the magnitude and direction. To find the vectors you first find the magnitude by using the equation below. |v|= (x^2 x^1)^2+(y^2+y^1)^2. Then after solving for the magnitude one can then find the distance. In a parametric you have an extra variable which is (t) usually known as time. First you solve for (t) then (x) and (y). Parametric is 3 factors x, y, and t that affects the coordinates. In polar equations one uses the unit circle to find the coordinates and it also consist of the assistance of the degree.