Trigonometry Basics Right Triangle Trigonometry Sine Function When

Trigonometry Basics Right Triangle Trigonometry

Sine Function • When you talk about the sin of an angle, that means you are working with the opposite side, and the hypotenuse of a right triangle.

The Trigonometric Functions we will be looking at SINE COSINE TANGENT

The Trigonometric Functions SINE COSINE TANGENT

SINE Pronounced “sign”

COSINE Pronounced “co-sign”

TANGENT Pronounced “tan-gent”

Greek Letter Prounounced “theta” Represents an unknown angle

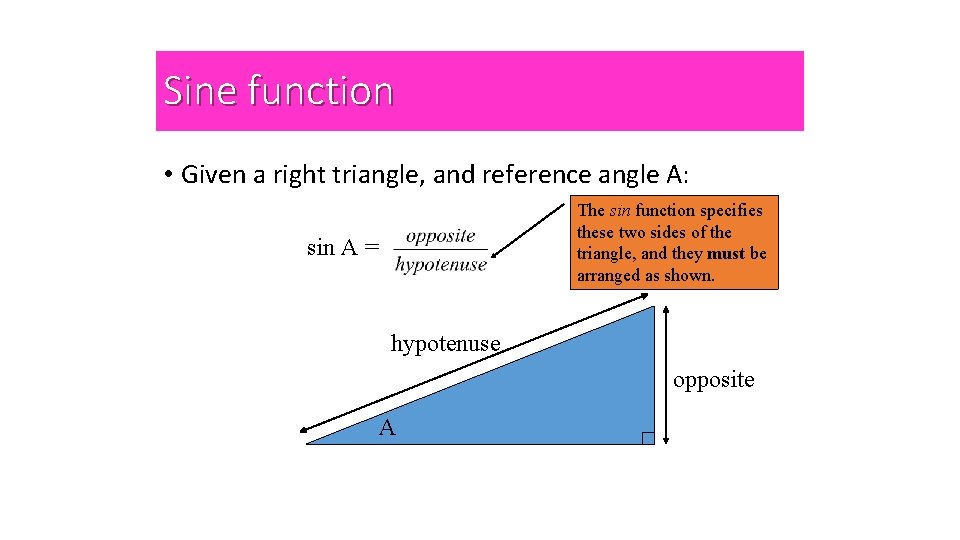
Sine function • Given a right triangle, and reference angle A: The sin function specifies these two sides of the triangle, and they must be arranged as shown. sin A = hypotenuse opposite A

Sine Function • For example to evaluate sin 40°… • Type-in 40 on your calculator (make sure the calculator is in degree mode), then press the sin key. • It should show a result of 0. 642787… • Note: If this did not work on your calculator, try pressing the sin key first, then type-in 40. Press the = key to get the answer.

Finding sin, cos, and tan. (Just writing a ratio or decimal. )

Sine. Function • Try each of these on your calculator: • sin 55° • sin 10° • sin 87°

Sine Function Try each of these on your calculator: n sin 55° = 0. 819 n sin 10° = 0. 174 n sin 87° = 0. 999 n

Inverse Sine. Function • Using sin-1 (inverse sin): If then 0. 7315 sin-1 (0. 7315) = • Solve for θ if sin θ = 0. 2419 = θ sin θ

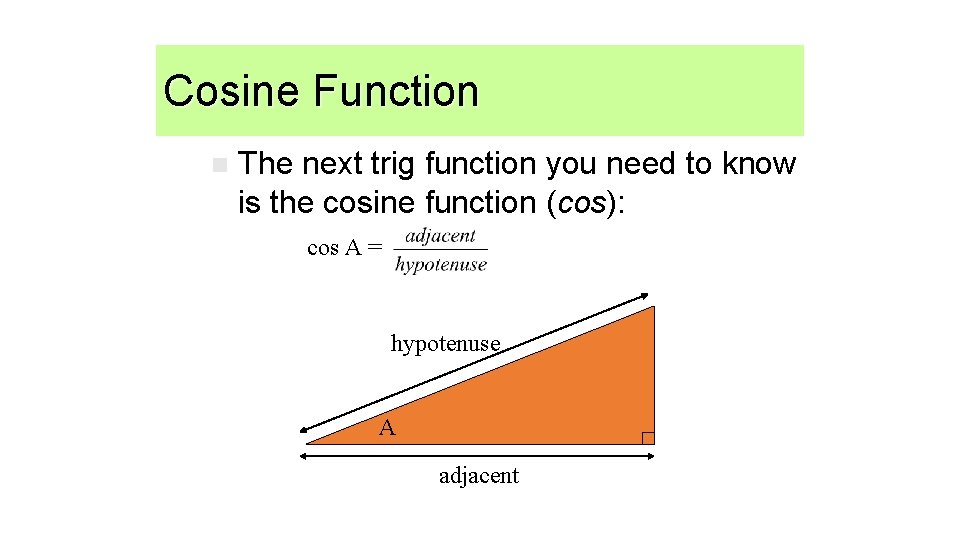
Cosine function Cosine Function n The next trig function you need to know is the cosine function (cos): cos A = hypotenuse A adjacent

Cosine Function • Use your calculator to determine cos 50° • First, type-in 50… • …then press the cos key. • You should get an answer of 0. 642787. . . • Note: If this did not work on your calculator, try pressing the cos key first, then type-in 50. Press the = key to get the answer.

Cosine Function • Try these on your calculator: • cos 25° • cos 0° • cos 90° • cos 45°

Cosine Function Try these on your calculator: n cos 25° = 0. 906 n cos 0° = 1 n cos 90° = 0 n cos 45° = 0. 707 n

Inverse Cosine Function • Using cos-1 (inverse cosine): If then 0. 9272 cos-1 (0. 9272) = • Solve for θ if cos θ = 0. 5150 = θ cos θ

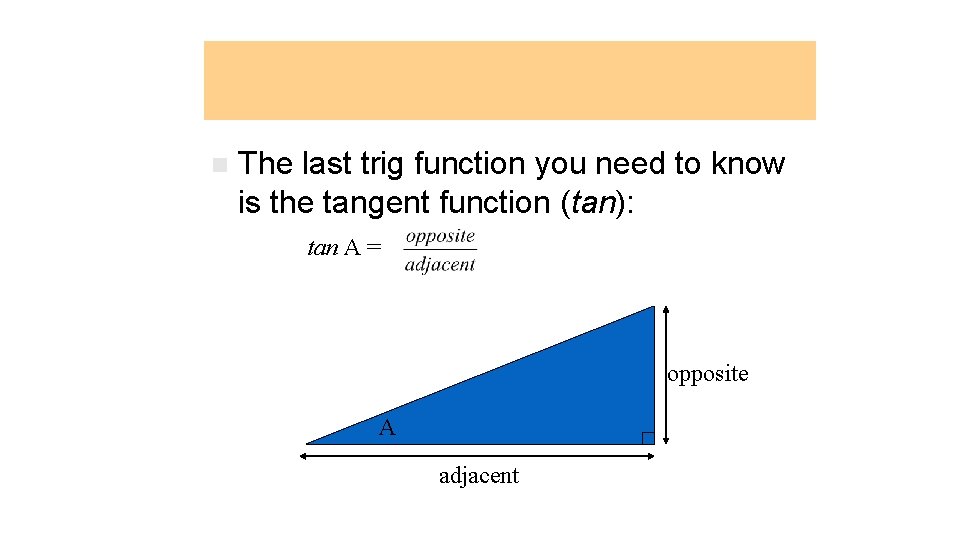
Tangent function Function n The last trig function you need to know is the tangent function (tan): tan A = opposite A adjacent

Tangent Function Use your calculator to determine tan 40° n First, type-in 40… n …then press the tan key. n You should get an answer of 0. 839. . . n ¨ Note: If this did not work on your calculator, try pressing the tan key first, then type-in 40. Press the = key to get the answer.

Tangent Function Try these on your calculator: n tan 5° n tan 30° n tan 85° n

Tangent Function Try these on your calculator: n tan 5° = 0. 087 n tan 30° = 0. 577 n tan 80° = 5. 671 n tan 85° = 11. 430 n

hypotenuse adjacent opposite

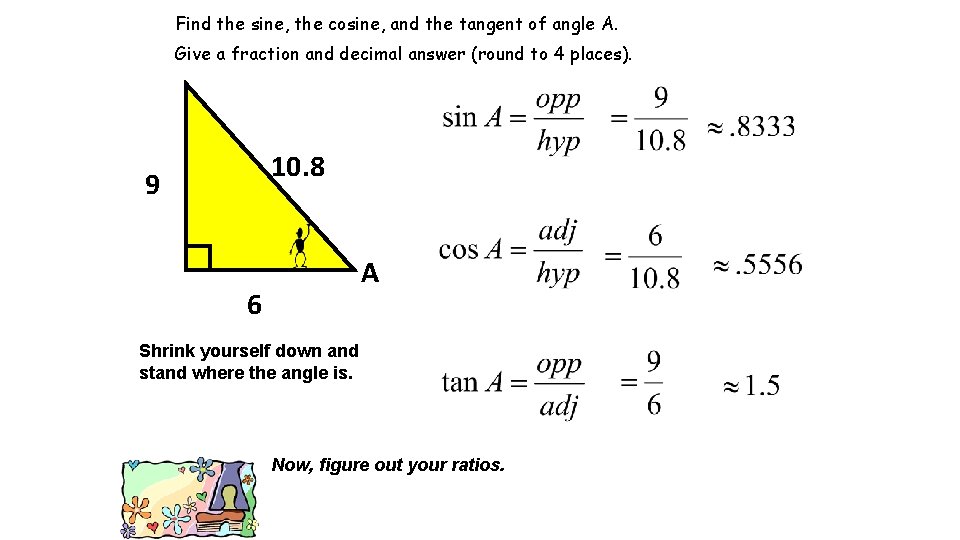
Find the sine, the cosine, and the tangent of angle A. Give a fraction and decimal answer (round to 4 places). 10. 8 9 A 6 Shrink yourself down and stand where the angle is. Now, figure out your ratios.

Find the sine, the cosine, and the tangent of angle A 8. 2 24. 5 Give a fraction and decimal answer (round to 4 decimal places). A 23. 1 Shrink yourself down and stand where the angle is. Now, figure out your ratios.

Finding a side. (Figuring out which ratio to use and getting to use a trig button. )

Ex: 1 Figure out which ratio to use. Find x. Round to the nearest tenth. 20 m x 20 tan Shrink yourself down and stand where the angle is. 55 ) Now, figure out which trig ratio you have and set up the problem.

Ex: 2 Find the missing side. Round to the nearest tenth. 80 ft x 80 ( tan 72 Shrink yourself down and stand where the angle is. Now, figure out which trig ratio you have and set up the problem. ) ) =

Ex: 3 Find the missing side. Round to the nearest tenth. x 283 m Shrink yourself down and stand where the angle is. Now, figure out which trig ratio you have and set up the problem.

Ex: 4 Find the missing side. Round to the nearest tenth. 20 ft x

Inverse Tangent Function • Using tan-1 (inverse tangent): If then 0. 5543 tan-1 (0. 5543) = • Solve for θ if tan θ = 28. 64 = θ tan θ

Finding an angle. (Figuring out which ratio to use and getting to use the 2 nd button and one of the trig buttons. )

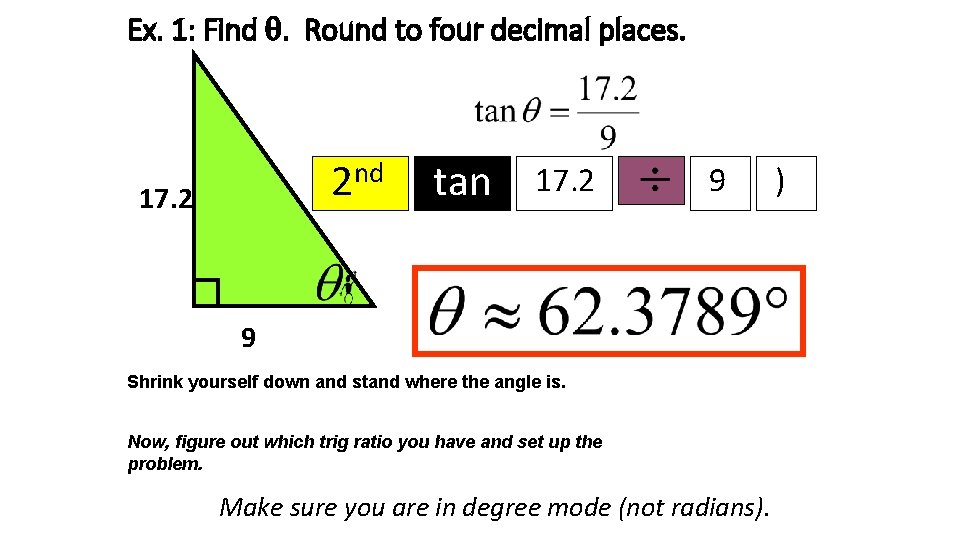
Ex. 1: Find . Round to four decimal places. 2 nd 17. 2 tan 17. 2 9 9 Shrink yourself down and stand where the angle is. Now, figure out which trig ratio you have and set up the problem. Make sure you are in degree mode (not radians). )

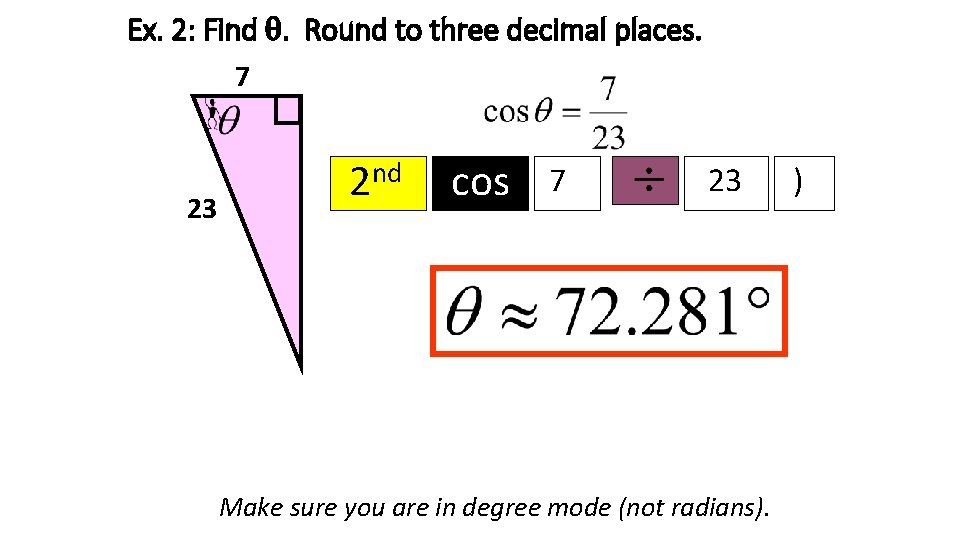
Ex. 2: Find . Round to three decimal places. 7 23 2 nd cos 7 23 Make sure you are in degree mode (not radians). )

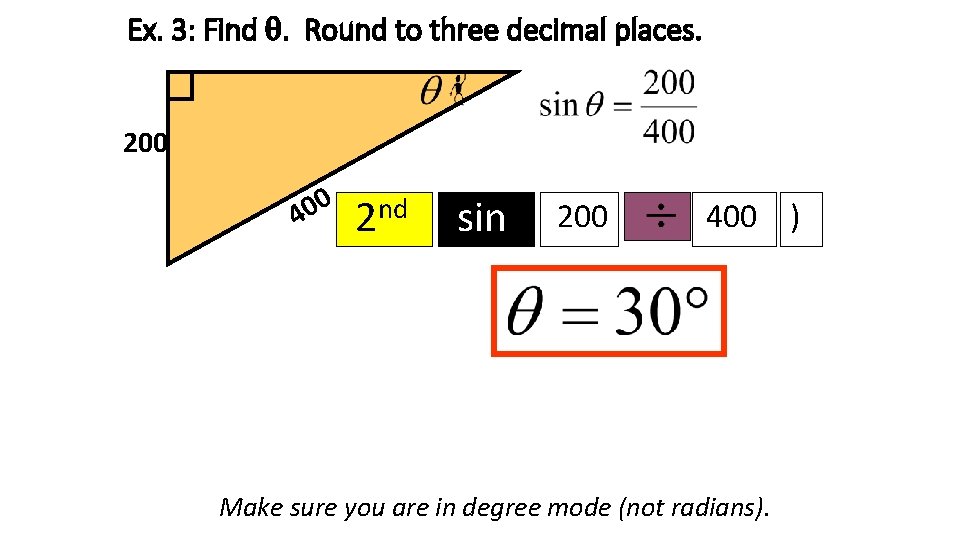
Ex. 3: Find . Round to three decimal places. 200 0 0 4 2 nd sin 200 400 ) Make sure you are in degree mode (not radians).

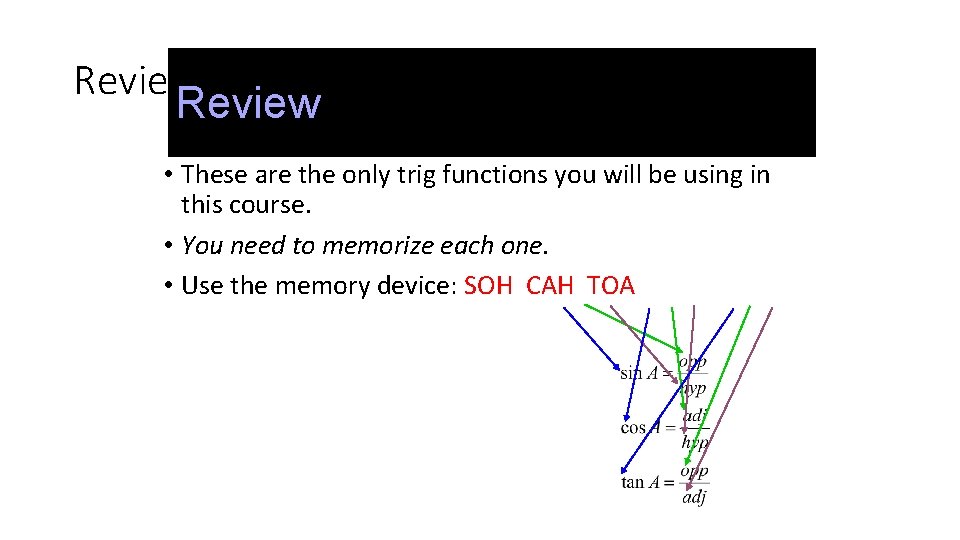
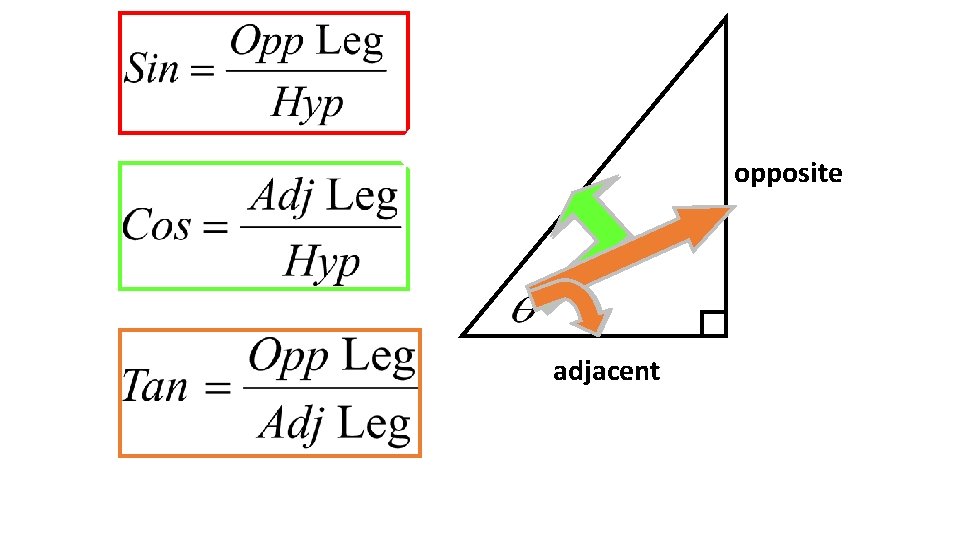
Review • These are the only trig functions you will be using in this course. • You need to memorize each one. • Use the memory device: SOH CAH TOA

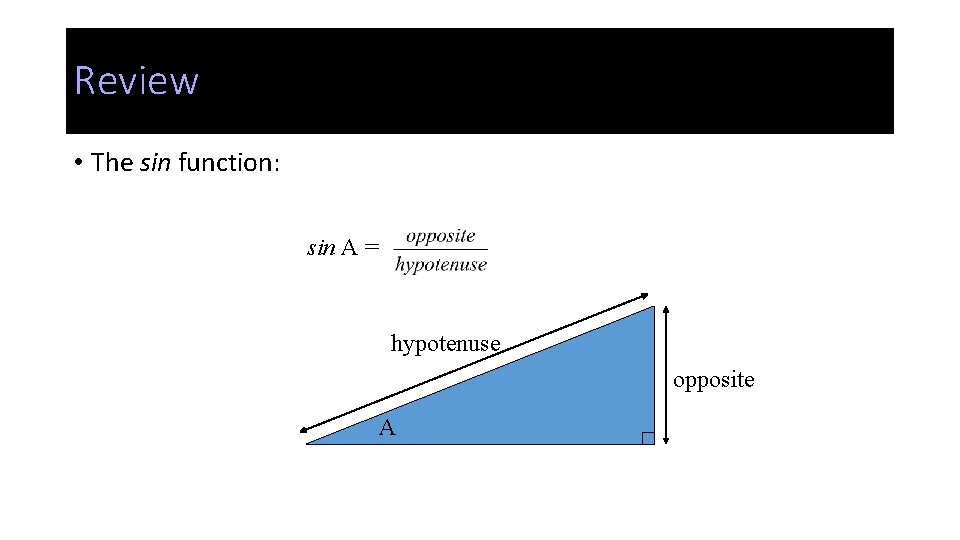
Review • The sin function: sin A = hypotenuse opposite A

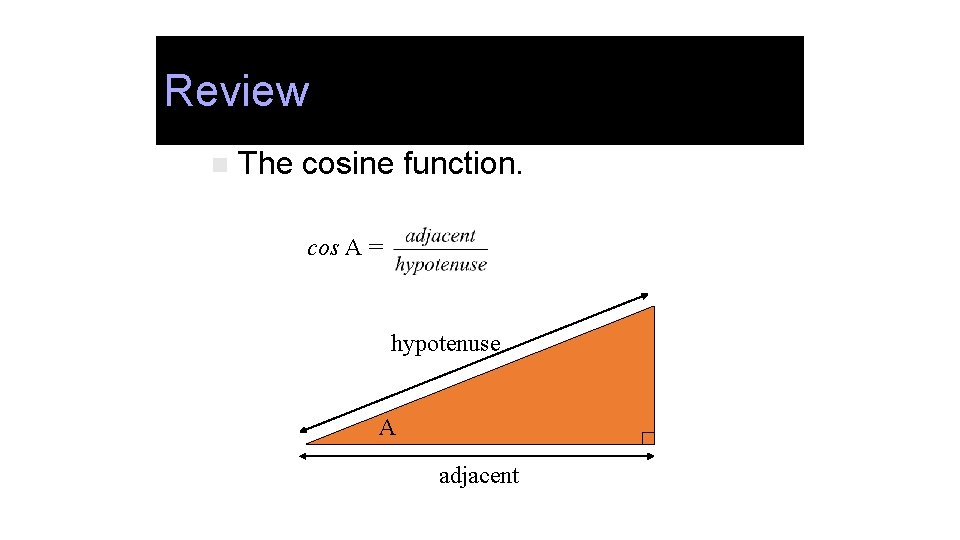
Review n The cosine function. cos A = hypotenuse A adjacent

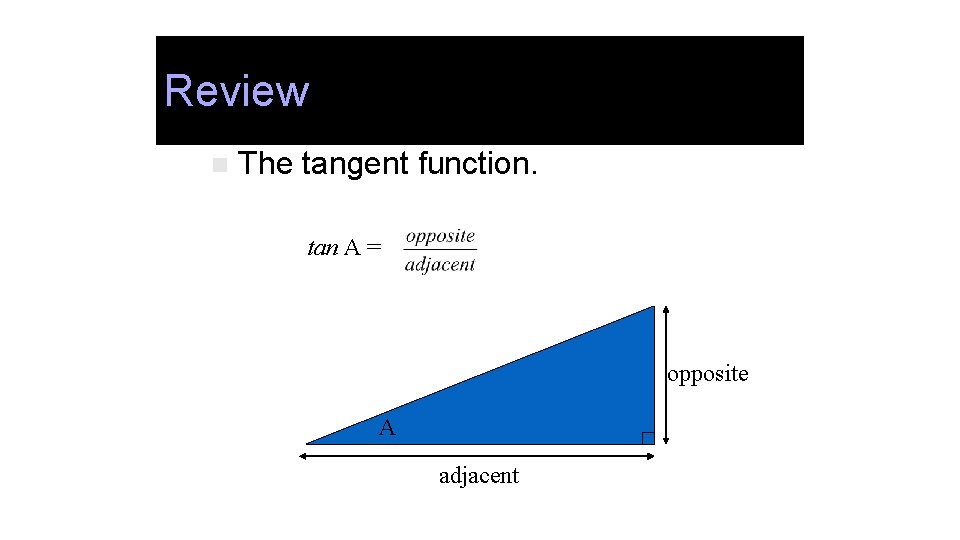
Review n The tangent function. tan A = opposite A adjacent

We need a way to remember all of these ratios…

When we are trying to find a side we use sin, cos, or tan. When we are trying to find an angle -1 -1 -1 we use sin , cos , or tan.