Trigonometry Addition formulas KUS objectives BAT derive the

Trigonometry: Addition formulas • KUS objectives BAT derive the double angle formulas BAT use the addition formulae to solve ‘show that’ problems BAT use the addition formulae to solve equations Starter:

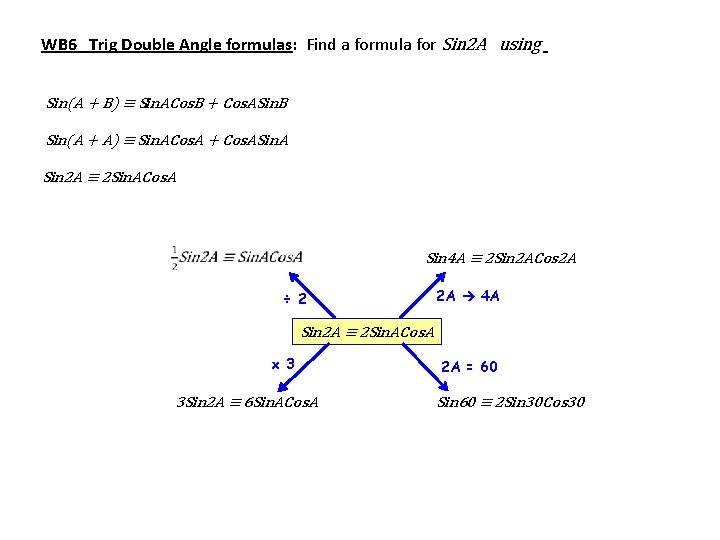
WB 6 Trig Double Angle formulas: Find a formula for Sin 2 A using Sin(A + B) ≡ Sin. ACos. B + Cos. ASin. B Sin(A + A) ≡ Sin. ACos. A + Cos. ASin. A Sin 2 A ≡ 2 Sin. ACos. A Sin 4 A ≡ 2 Sin 2 ACos 2 A ÷ 2 2 A 4 A Sin 2 A ≡ 2 Sin. ACos. A x 3 3 Sin 2 A ≡ 6 Sin. ACos. A 2 A = 60 Sin 60 ≡ 2 Sin 30 Cos 30

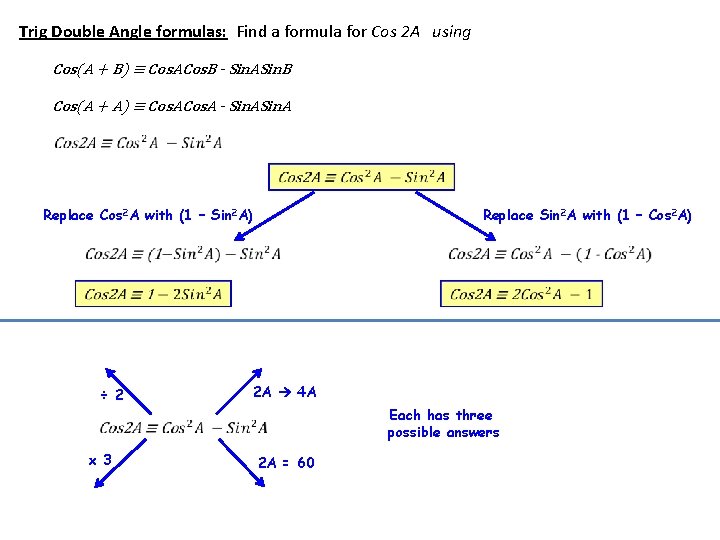
Trig Double Angle formulas: Find a formula for Cos 2 A using Cos(A + B) ≡ Cos. ACos. B - Sin. ASin. B Cos(A + A) ≡ Cos. A - Sin. A Replace Cos 2 A with (1 – Sin 2 A) ÷ 2 Replace Sin 2 A with (1 – Cos 2 A) 2 A 4 A Each has three possible answers x 3 2 A = 60

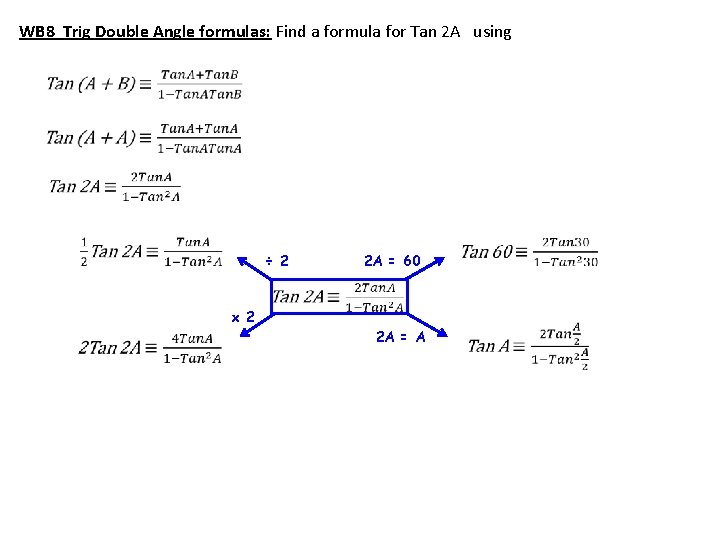
WB 8 Trig Double Angle formulas: Find a formula for Tan 2 A using ÷ 2 2 A = 60 x 2 2 A = A

2θ θ Replace the first part Rewrite

Double the angle parts Replace cos 4θ The 1 s cancel out

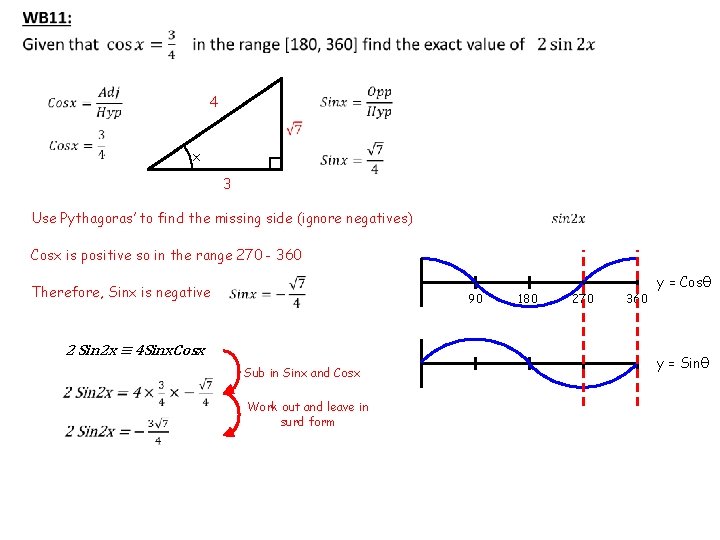
4 x 3 Use Pythagoras’ to find the missing side (ignore negatives) Cosx is positive so in the range 270 - 360 Therefore, Sinx is negative 90 2 Sin 2 x ≡ 4 Sinx. Cosx Sub in Sinx and Cosx Work out and leave in surd form 180 270 360 y = Cosθ y = Sinθ

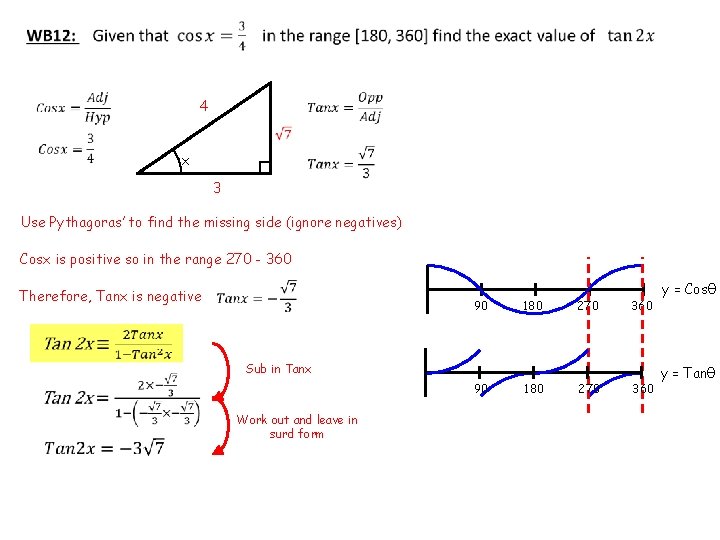
4 x 3 Use Pythagoras’ to find the missing side (ignore negatives) Cosx is positive so in the range 270 - 360 Therefore, Tanx is negative 90 180 270 360 Sub in Tanx 90 Work out and leave in surd form 180 270 360 y = Cosθ y = Tanθ

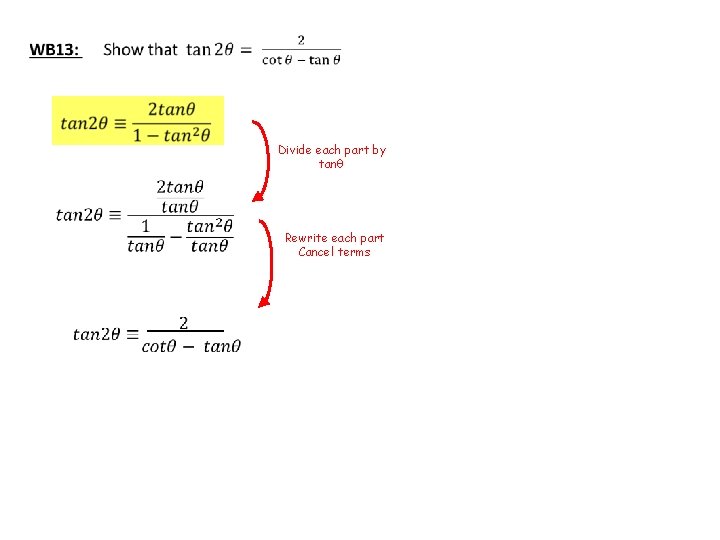
Divide each part by tanθ Rewrite each part Cancel terms

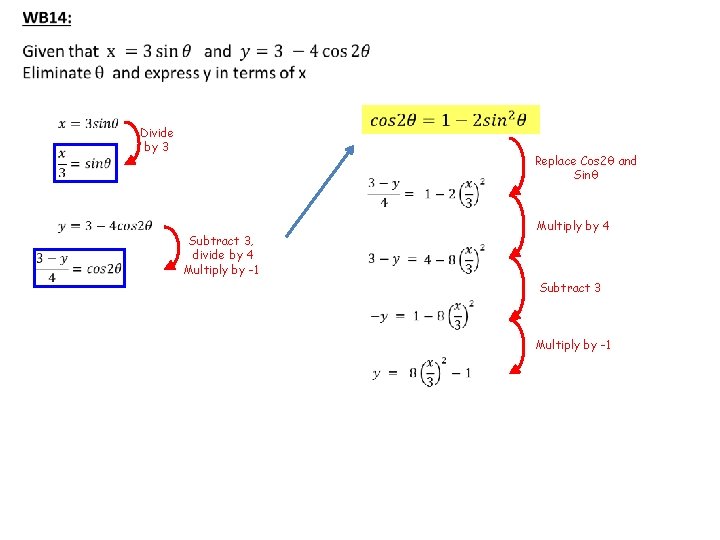
Divide by 3 Replace Cos 2θ and Sinθ Subtract 3, divide by 4 Multiply by -1 Multiply by 4 Subtract 3 Multiply by -1

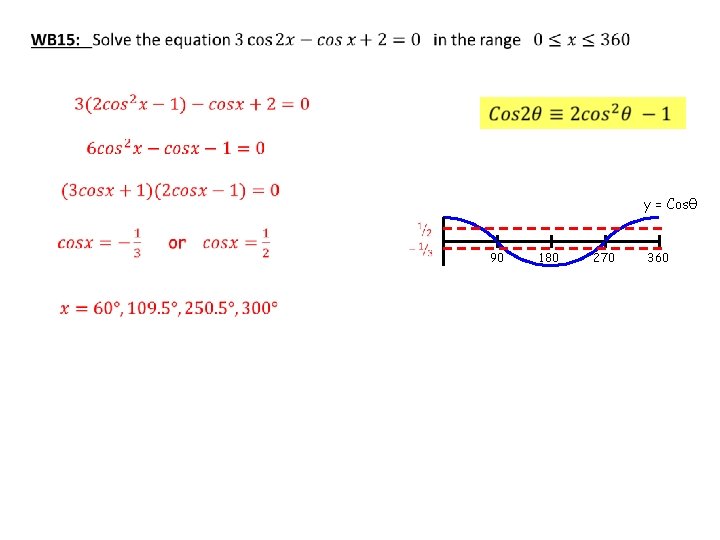
y = Cosθ 90 180 270 360

• KUS objectives BAT derive the double angle formulas BAT use the addition formulae to solve ‘show that’ problems BAT use the addition formulae to solve equations self-assess using: R / A / G ‘I am now able to ____. To improve I need to be able to ____’