Trigonometric Ratios In Trigonometry the comparison is between

Trigonometric Ratios In Trigonometry, the comparison is between sides of a triangle. Used to find a side of a right triangle given 1 side and 1 acute angle

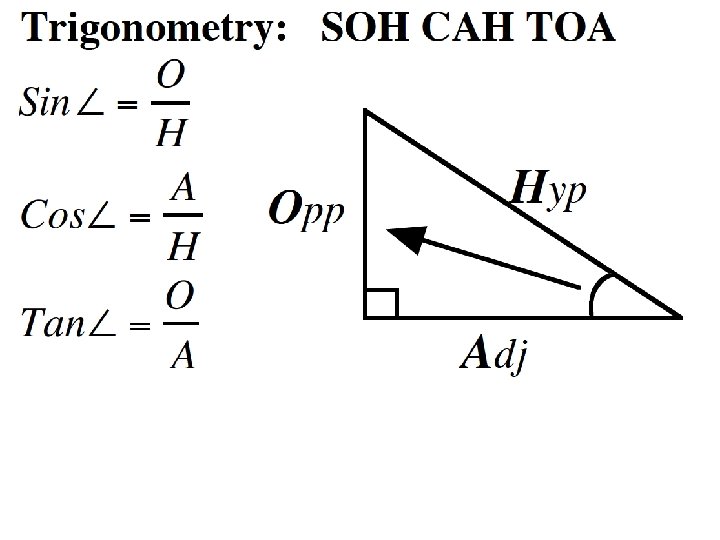
Three Trigonometric Ratios • Sine – abbreviated ‘sin’. – Ratio: sin θ = opposite side hypotenuse Θ this is the symbol for an unknown angle measure. It’s name is ‘Theta’. • Cosine - abbreviated ‘cos’. – Ratio: cos θ = adjacent side hypotenuse • Tangent - abbreviated ‘tan’. – Ratio: tan θ = opposite side adjacent side Easy way to remember trig ratios: SOH CAH TOA
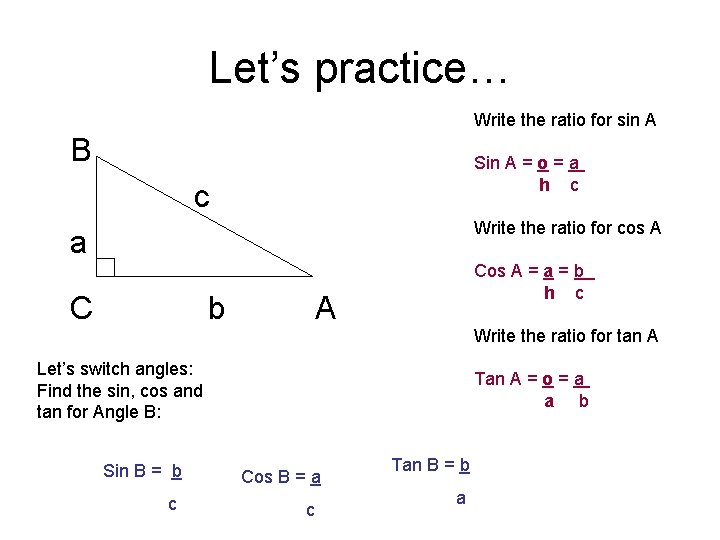
Let’s practice… Write the ratio for sin A B Sin A = o = a h c c Write the ratio for cos A a C b Cos A = a = b h c A Write the ratio for tan A Let’s switch angles: Find the sin, cos and tan for Angle B: Sin B = b c Tan A = o = a a b Cos B = a c Tan B = b a
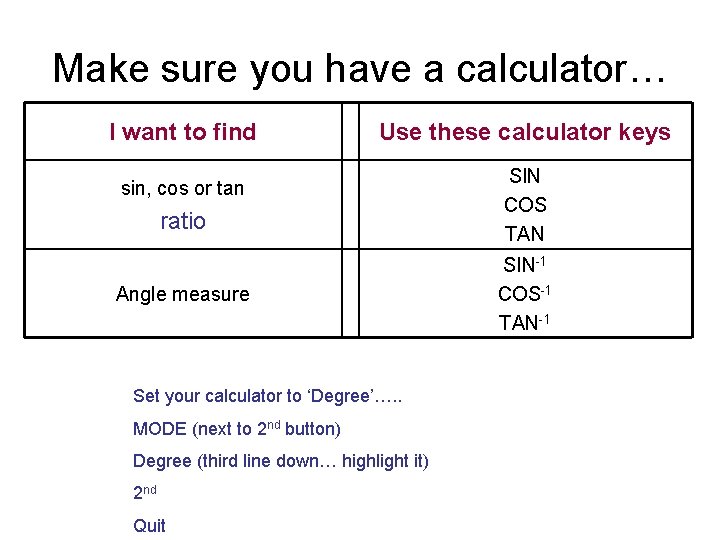
Make sure you have a calculator… I want to find Use these calculator keys sin, cos or tan ratio Angle measure Set your calculator to ‘Degree’…. . MODE (next to 2 nd button) Degree (third line down… highlight it) 2 nd Quit SIN COS TAN SIN-1 COS-1 TAN-1
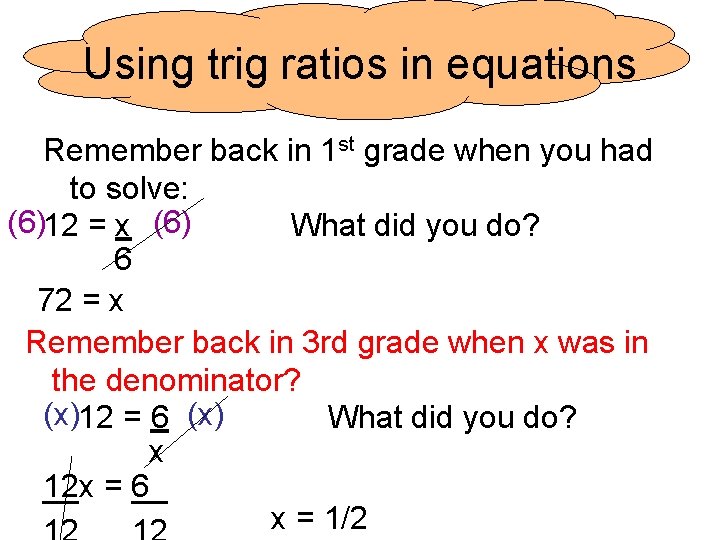
Using trig ratios in equations Remember back in 1 st grade when you had to solve: (6)12 = x (6) What did you do? 6 72 = x Remember back in 3 rd grade when x was in the denominator? (x)12 = 6 (x) What did you do? x 12 x = 6 __ __ x = 1/2

Trigonometric Ratios • When do we use them? – On right triangles that are NOT 45 -45 -90 or 30 -60 -90 Find: tan 45 1 Why? tan = opp hyp

Example: Find the value of x. Step 1: Mark the “Angle of Perspective”. Step 2: Label the sides (Hyp / Opp / Adj). Step 3: Select a trigonometry ratio (sin/ cos / tan). Sin = Step 4: Substitute the values into the equation. Sin 25 = If the variable is on top multiply If the variable is on the bottom Divide Step 5: Solve the equation : x = 12 Sin (25 x = 5. 07 cm opp Hyp Angle of Perspective Adj

Ask yourself: In relation to the angle, what pieces do I have? 34° 15 cm Opposite and hypotenuse Ask yourself: x cm What trig ratio uses Opposite and Hypotenuse? SINE Set up the equation and solve: (15) Sin 34 = x (15) 15 (15)Sin 34 = x 8. 39 cm = x

Ask yourself: In relation to the angle, what pieces do I have? 53° 12 cm Opposite and adjacent x cm Ask yourself: What trig ratio uses Opposite and adjacent? tangent Set up the equation and solve: (12)Tan 53 = x (12) 12 (12)tan 53 = x 15. 92 cm = x
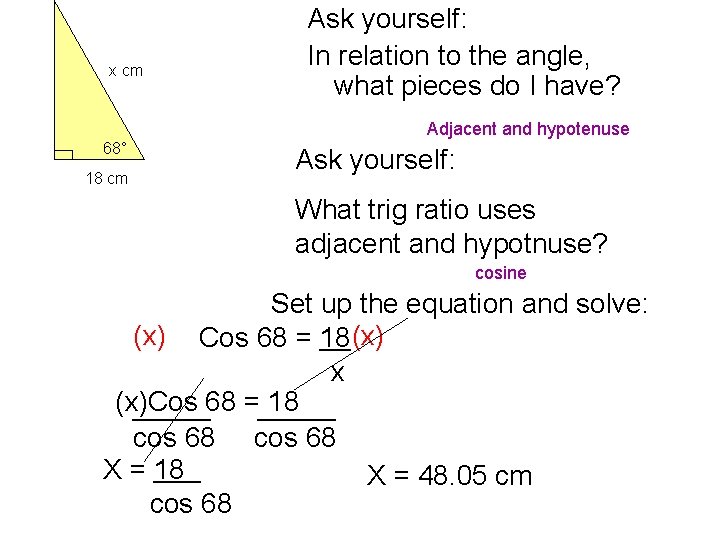
x cm Ask yourself: In relation to the angle, what pieces do I have? Adjacent and hypotenuse 68° 18 cm Ask yourself: What trig ratio uses adjacent and hypotnuse? cosine Set up the equation and solve: (x) Cos 68 = 18 (x) x (x)Cos 18 _____68 =_____ cos 68 X = 18 X = 48. 05 cm cos 68
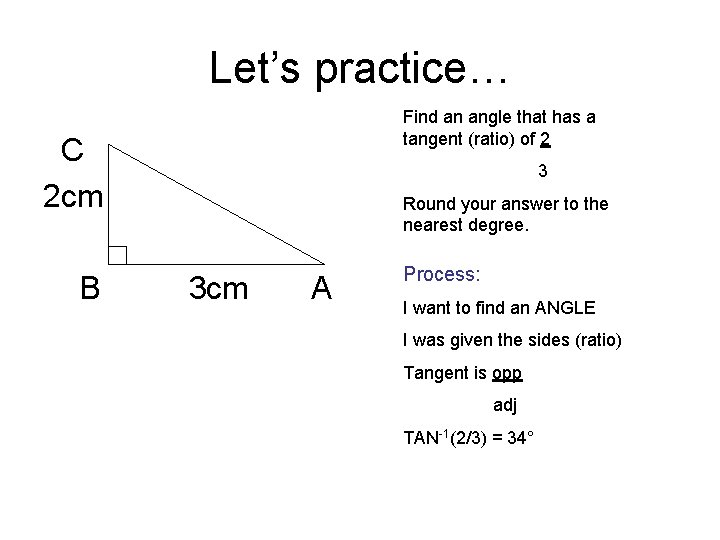
Let’s practice… Find an angle that has a tangent (ratio) of 2 C 2 cm B 3 Round your answer to the nearest degree. 3 cm A Process: I want to find an ANGLE I was given the sides (ratio) Tangent is opp adj TAN-1(2/3) = 34°
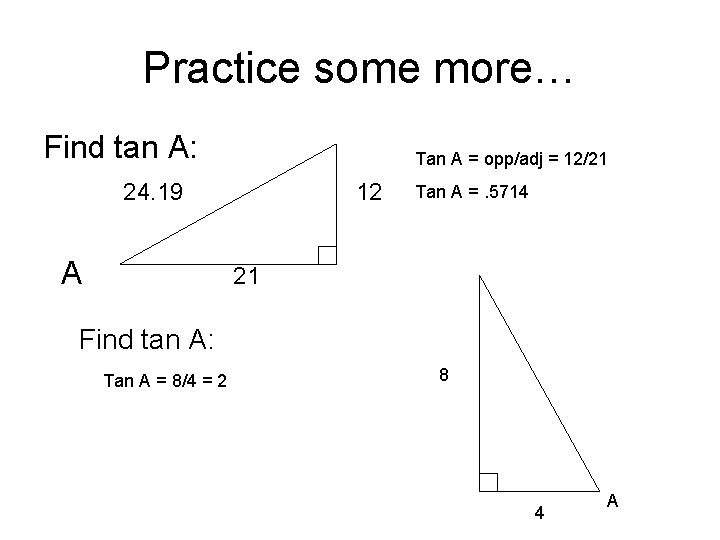
Practice some more… Find tan A: Tan A = opp/adj = 12/21 24. 19 A 12 Tan A =. 5714 21 Find tan A: Tan A = 8/4 = 2 8 4 A
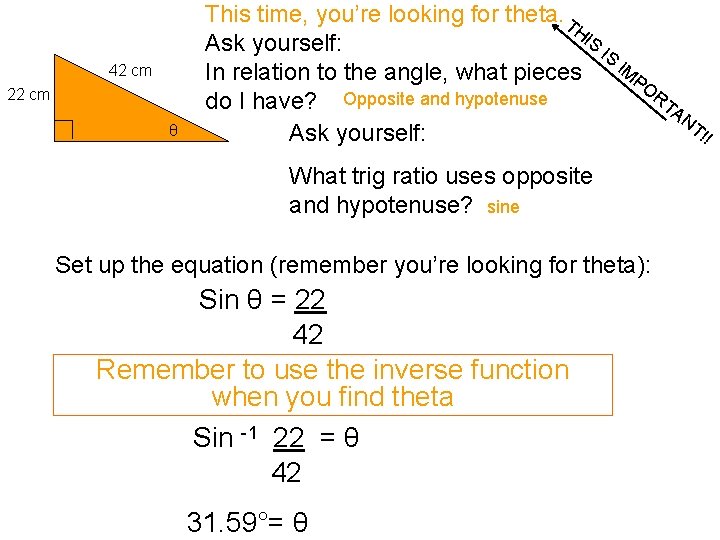
42 cm 22 cm θ This time, you’re looking for theta. T HI S Ask yourself: IS In relation to the angle, what pieces IMPO RT do I have? Opposite and hypotenuse AN T! Ask yourself: ! What trig ratio uses opposite and hypotenuse? sine Set up the equation (remember you’re looking for theta): Sin θ = 22 42 Remember to use the inverse function when you find theta Sin -1 22 = θ 42 31. 59°= θ
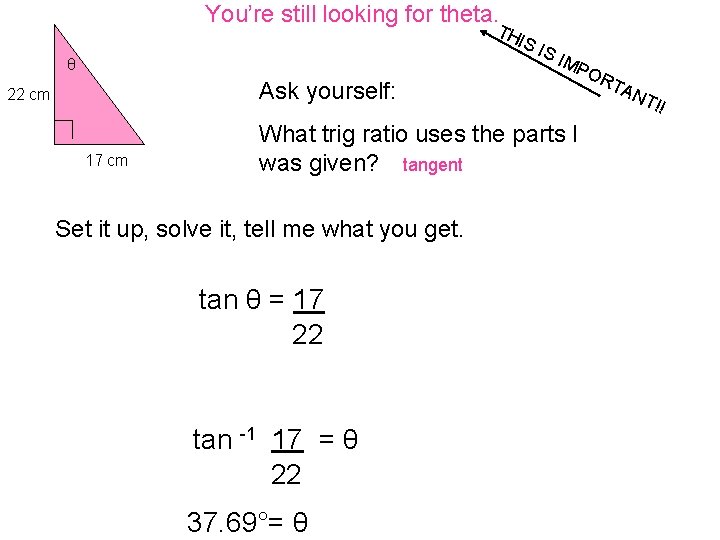
You’re still looking for theta. TH IS θ IS IMP Ask yourself: 22 cm 17 cm What trig ratio uses the parts I was given? tangent Set it up, solve it, tell me what you get. tan θ = 17 22 tan -1 17 = θ 22 37. 69°= θ OR T AN T!!
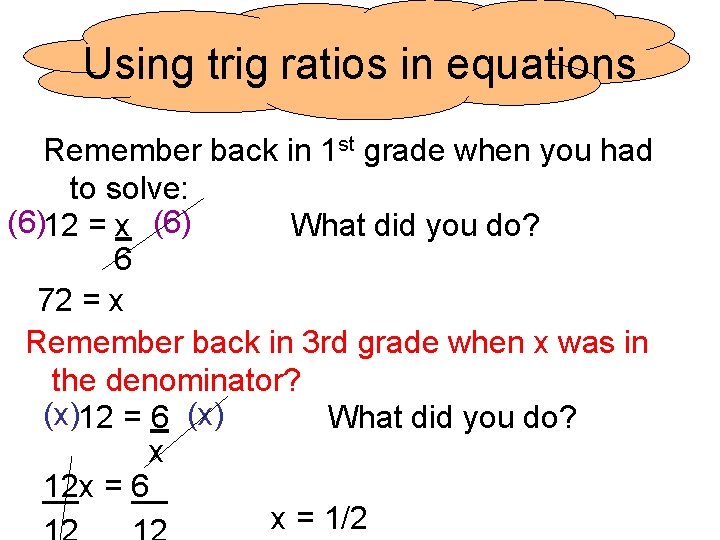
Using trig ratios in equations Remember back in 1 st grade when you had to solve: (6)12 = x (6) What did you do? 6 72 = x Remember back in 3 rd grade when x was in the denominator? (x)12 = 6 (x) What did you do? x 12 x = 6 __ __ x = 1/2

- Slides: 18


































