Trigonometric ratios In right triangles The segment across






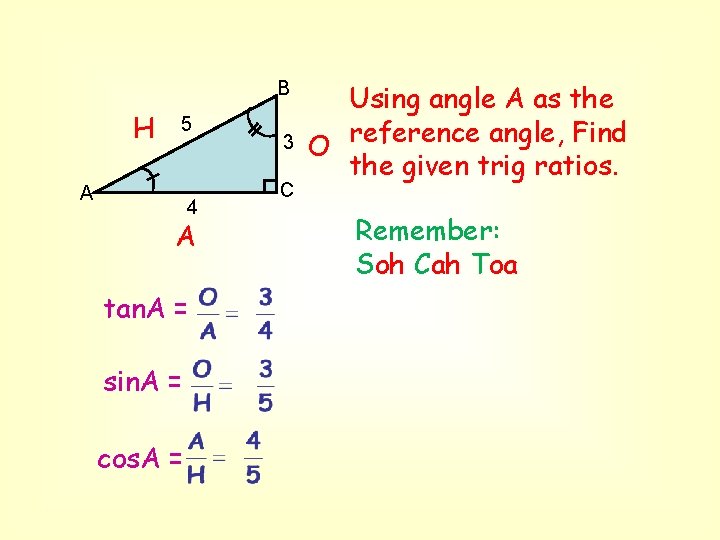





- Slides: 15

Trigonometric ratios

In right triangles : • The segment across from the right angle ( “Hyp. ”. ) is labeled the hypotenuse Hyp. Opp. Angle of Perspective Adj. • The “angle of perspective” determines how to label the sides. • Segment opposite from the Angle of Perspective( ) is labeled “Opp. ” • Segment adjacent to (next to) the Angle of Perspective ( ) is labeled “Adj. ”. * The angle of Perspective is never the right angle. Lesson 9. 5 Trigonometry Ratios 2

Labeling sides depends on the Angle of Perspective If is the Angle of Perspective then …… Angle of Perspective Hyp. Adj. Opp. *”Opp. ” means segment opposite from Angle of Perspective “Adj. ” means segment connected to Angle of Perspective Lesson 9. 5 Trigonometric Rations 3

If the Angle of Perspective is then Adj Hyp then Opp Lesson 9. 5 Trigonometry Ratios Hyp Adj 4

First, a little reference… In RIGHT triangle ABC, suppose you are standing at A. B Opposite C Hy po ten us Adjacent The longest side as you know is called the HYPOTENUSE. e A The leg nearest you is called the ADJACENT LEG. The leg farthest away is called the OPPOSITE LEG. Stop

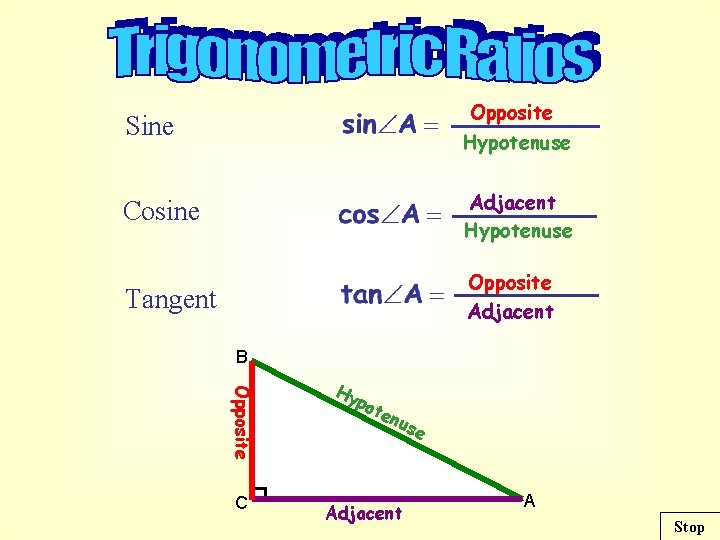
Opposite Sine Hypotenuse Cosine Adjacent Hypotenuse Tangent Opposite Adjacent B Opposite C Hy pot enu Adjacent se A Stop

os in an Stop

Sometimes, these are hard not to mix up. Most people just remember one thing… Pronounced “Soak a Toe…Ahhhhhh!” Stop
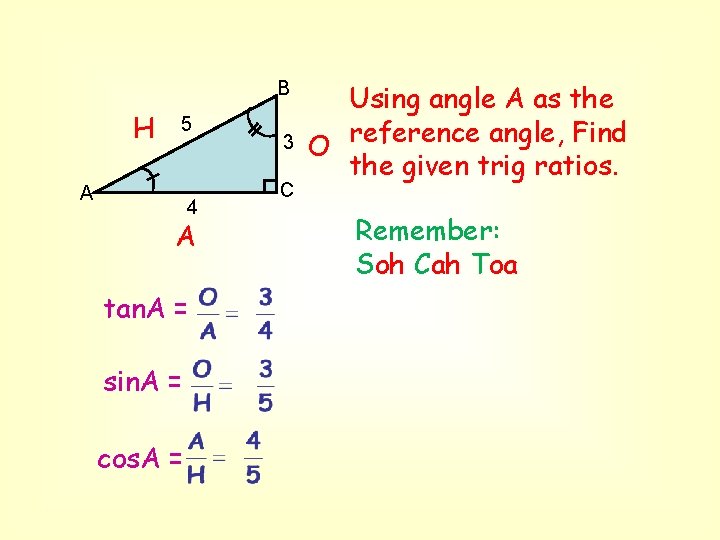
B H 5 A 4 A tan. A = sin. A = cos. A = 3 C Using angle A as the reference angle, Find O the given trig ratios. Remember: Soh Cah Toa

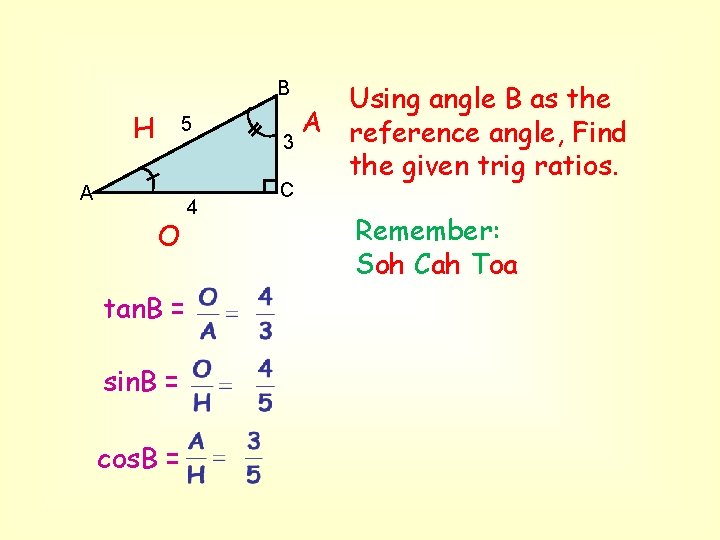
B H 5 A O tan. B = sin. B = cos. B = 4 Using angle B as the A reference angle, Find 3 the given trig ratios. C Remember: Soh Cah Toa

Trigonometry Ratios If Sin is the Angle of Perspective then …. . . = Hyp Opp Cos = tan = Adj Angle of Perspective Lesson 9. 5 Trigonometry Ratios 11

Trigonometric Procedures

1) Is this a right triangle? This is an important 1 st step!!! B 10 6 A C 8 1) Yes, the right angle symbol is in the picture or the problem states that you have a right angle. 2. Label angle of perspective and sides. Hypotenuse Opposite Leg Adjacent leg 3) Think SOH CAH TOA B opp 6 Hyp 10 C adj 8 A

EXAMPLE: Use trig to find the length of the missing side. 1) Think! *Right Triangle? *What sides and angles do you have? *Can you use Pythagorean? 2) Label! *Angle of perspective * Hypotenuse, Opposite, Adjacent 3) Select ratio and substitute values 4) Solve for the variable! Cross Multiply and solve for x 5) Calculate! x 18 40° opp x hyp 18 40°

Solving Trigonometric Equations Sin ∠= O Sin 25° = H x = (12) (Sin 25) x = 5. 071 cm O Sin 25° = Sin 25 = H Sin ∠ = = x = 28. 394 cm Lesson 9. 5 Trigonometric Rations 15