Trigonometric Polar Form of Complex Numbers How is

Trigonometric (Polar) Form of Complex Numbers

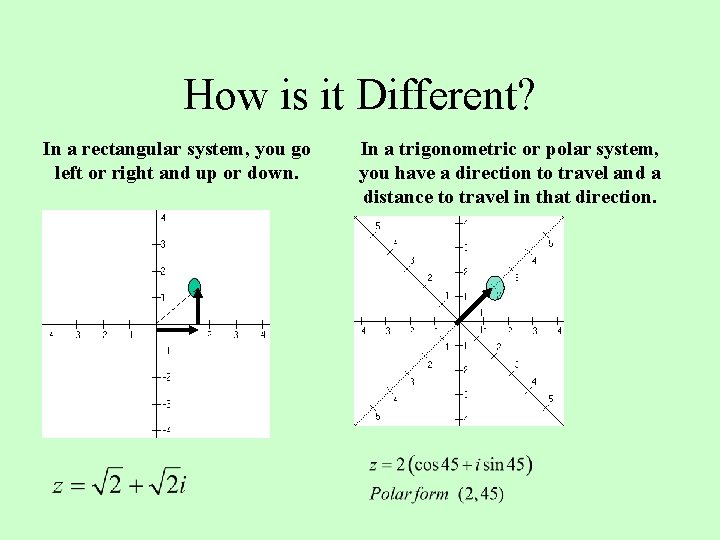
How is it Different? In a rectangular system, you go left or right and up or down. In a trigonometric or polar system, you have a direction to travel and a distance to travel in that direction.

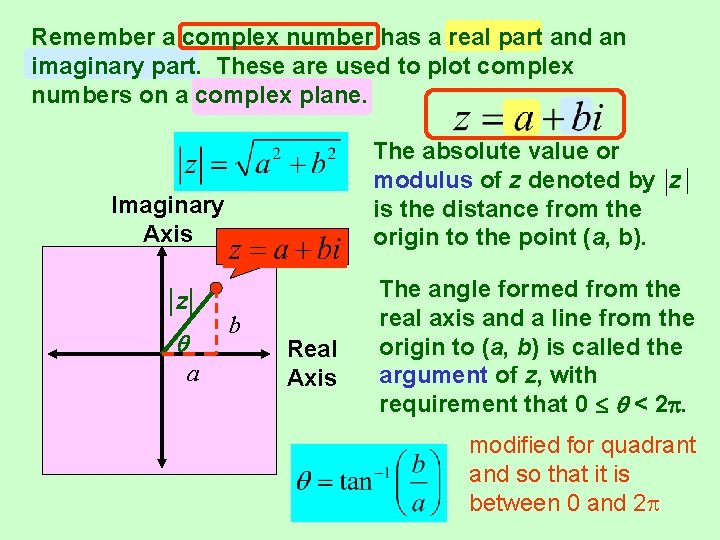
Remember a complex number has a real part and an imaginary part. These are used to plot complex numbers on a complex plane. The absolute value or modulus of z denoted by z is the distance from the origin to the point (a, b). Imaginary Axis z a b Real Axis The angle formed from the real axis and a line from the origin to (a, b) is called the argument of z, with requirement that 0 < 2. modified for quadrant and so that it is between 0 and 2

Trigonometric Form of a Complex Number r b a Note: You may use any other trig functions and their relationships to the right triangle as well as tangent.

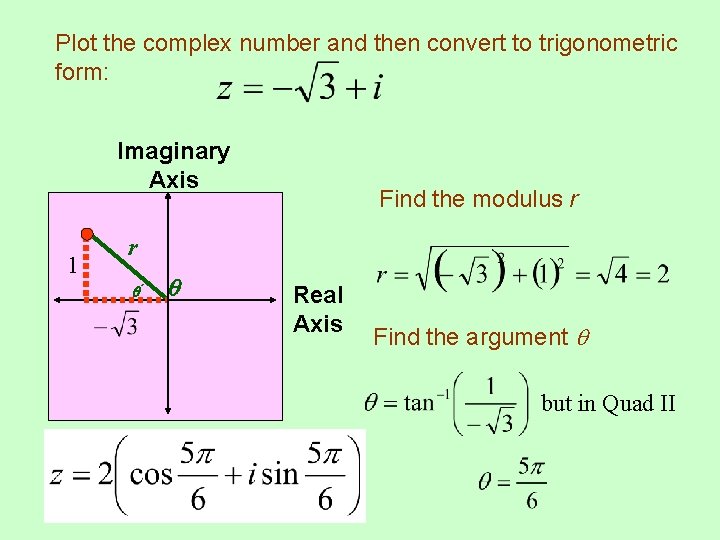
Plot the complex number and then convert to trigonometric form: Imaginary Axis 1 Find the modulus r r Real Axis Find the argument but in Quad II

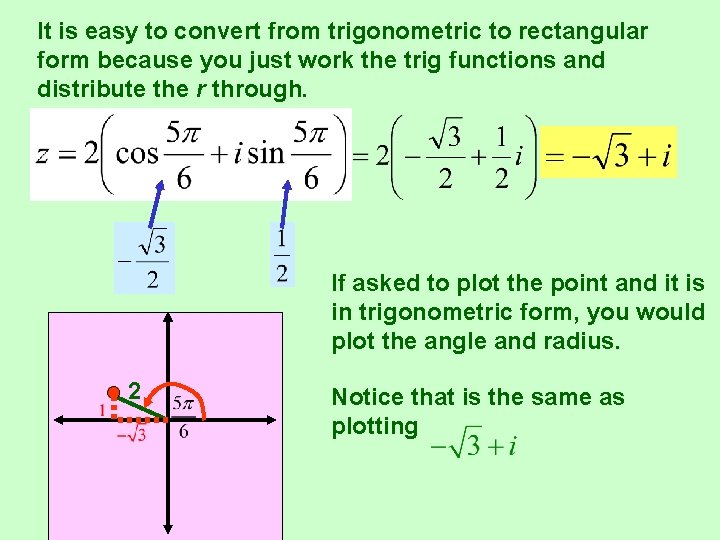
It is easy to convert from trigonometric to rectangular form because you just work the trig functions and distribute the r through. If asked to plot the point and it is in trigonometric form, you would plot the angle and radius. 2 Notice that is the same as plotting

Graphing Utility: Write the complex number in standard form a + bi. [2 nd]

Multiplying Complex Numbers To multiply complex numbers in rectangular form, you would FOIL and convert i 2 into – 1. To multiply complex numbers in trig form, you simply multiply the rs and thetas. The formulas are scarier than they are.

Let's try multiplying two complex numbers in trigonometric form together. Look at where we started and where we ended up and see if you can make a statement as to what happens to Must FOIL these two complex the r 's and the 's when you multiply numbers. Replace i 2 with -1 and group real terms and then imaginary terms Multiply the Moduli and Add the Arguments use sum formula for cos use sum formula for sin

Example Rectangular form Trig form

Dividing Complex Numbers In rectangular form, you rationalize using the complex conjugate. In trig form, you just divide the rs and subtract theta.

(This says to multiply two complex numbers in polar form, multiply the moduli and add the arguments) (This says to divide two complex numbers in polar form, divide the moduli and subtract the arguments)

multiply the moduli add the arguments (the i sine term will have same argument) If you want the answer in rectangular coordinates simply compute the trig functions and multiply the 24 through.

divide the moduli subtract the arguments In polar form we want an angle between 0 and 360° so add 360° to the -80° In rectangular coordinates:

Example Rectangular form Trig form

Powers of Complex Numbers This is horrible in rectangular form. The best way to expand one of these is using Pascal’s triangle and binomial expansion. You’d need to use an ichart to simplify. It’s much nicer in trig form. You just raise the r to the power and multiply theta by the exponent.

Roots of Complex Numbers • There will be as many answers as the index of the root you are looking for – Square root = 2 answers – Cube root = 3 answers, etc. • Answers will be spaced symmetrically around the circle – You divide a full circle by the number of answers to find out how far apart they are

General Process 1. Problem must be in trig form 2. Take the nth root of n. All answers have the same value for n. 3. Divide theta by n to find the first angle. 4. Divide a full circle by n to find out how much you add to theta to get to each subsequent answer.

The formula k starts at 0 and goes up to n-1 This is easier than it looks.

Example 1. Find the 4 th root of 81 2. Divide theta by 4 to get the first angle. 3. Divide a full circle (360) by 4 to find out how far apart the answers are. 4. List the 4 answers. • The only thing that changes is the angle. • The number of answers equals the number of roots.