Trigonometric Method of Adding Vectors Analytic Method of

Trigonometric Method of Adding Vectors

Analytic Method of Addition Resolution of vectors into components: YOU MUST KNOW & UNDERSTAND TRIGONOMETERY TO UNDERSTAND THIS!!!!

Vector Components • Any vector can be expressed as the sum of two other vectors, called its components. Usually, the other vectors are chosen so that they are perpendicular to each other. • Consider the vector V in a plane (say, the xy plane) • We can express V in terms of COMPONENTS Vx , Vy • Finding THE COMPONENTS Vx & Vy is EQUIVALENT to finding 2 mutually perpendicular vectors which, when added (with vector addition) will give V.

• We can express any vector V in terms of COMPONENTS Vx , Vy • Finding Vx & Vy is EQUIVALENT to finding 2 mutually perpendicular vectors which, when added (with vector addition) will give V.

• We can express any vector V in terms of COMPONENTS Vx , Vy • Finding Vx & Vy is EQUIVALENT to finding 2 mutually perpendicular vectors which, when added (with vector addition) will give V. • That is, we want to find Vx & Vy such that V Vx + V y (Vx || x axis, Vy || y axis) Finding Components “Resolving into Components”

• Mathematically, a component is a projection of a vector along an axis. – Any vector can be completely described by its components • It is useful to use Rectangular Components – These are the projections of the vector along the x- and y-axes

V is Resolved Into Components: Vx & Vy V Vx + Vy (Vx || x axis, Vy || y axis) • By the parallelogram method, clearly THE VECTOR SUM IS: V = Vx + Vy In 3 dimensions, we also need a Vz.

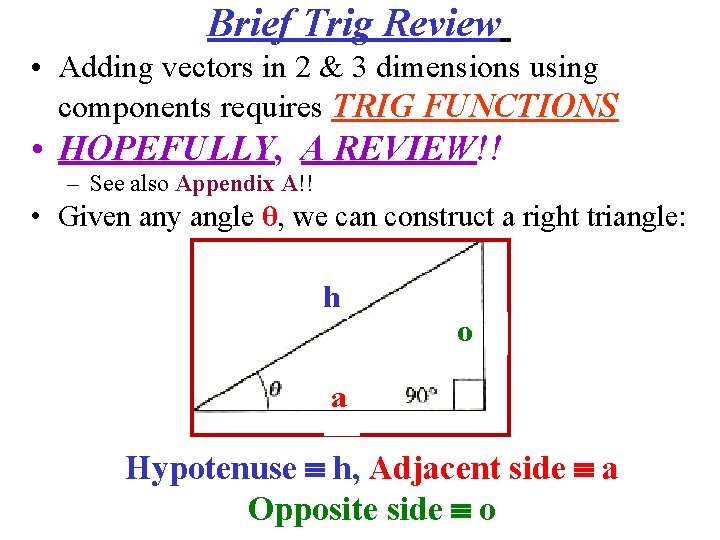
Brief Trig Review • Adding vectors in 2 & 3 dimensions using components requires TRIG FUNCTIONS • HOPEFULLY, A REVIEW!! – See also Appendix A!! • Given any angle θ, we can construct a right triangle: h o a Hypotenuse h, Adjacent side a Opposite side o

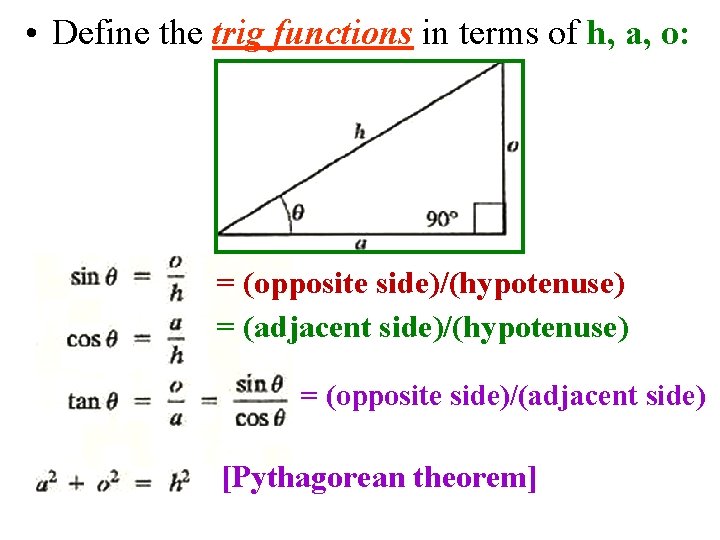
• Define the trig functions in terms of h, a, o: = (opposite side)/(hypotenuse) = (adjacent side)/(hypotenuse) = (opposite side)/(adjacent side) [Pythagorean theorem]

Trig Summary • Pythagorean Theorem: r 2 = x 2 + y 2 • Trig Functions: sin θ = (y/r), cos θ = (x/r) tan θ = (y/x) • Trig Identities: sin² θ + cos² θ = 1 • Other identities are in Appendix B & the back cover.

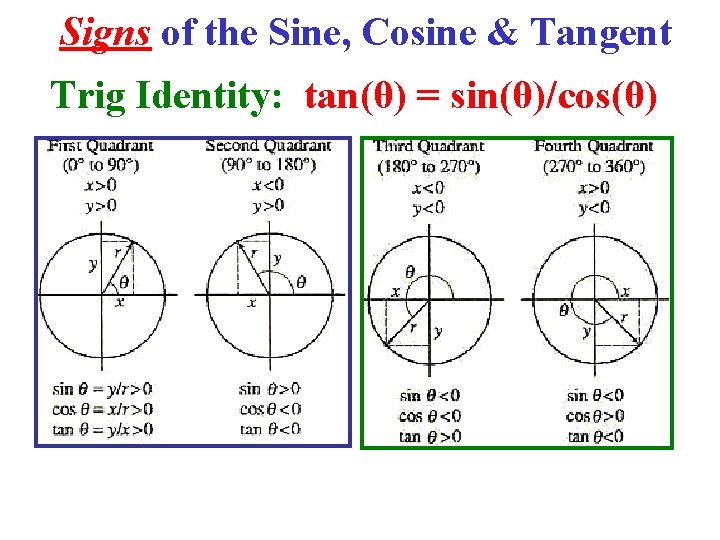
Signs of the Sine, Cosine & Tangent Trig Identity: tan(θ) = sin(θ)/cos(θ)

Inverse Functions and Angles • To find an angle, use an inverse trig function. • If sin = y/r then = sin-1 (y/r) • Also, angles in the triangle add up to 90° + = 90° • Complementary angles sin α = cos β

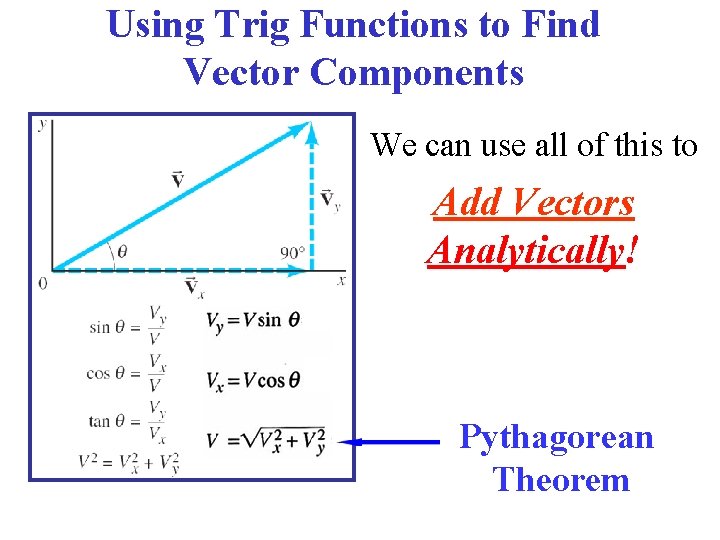
Using Trig Functions to Find Vector Components We can use all of this to Add Vectors Analytically! Pythagorean Theorem

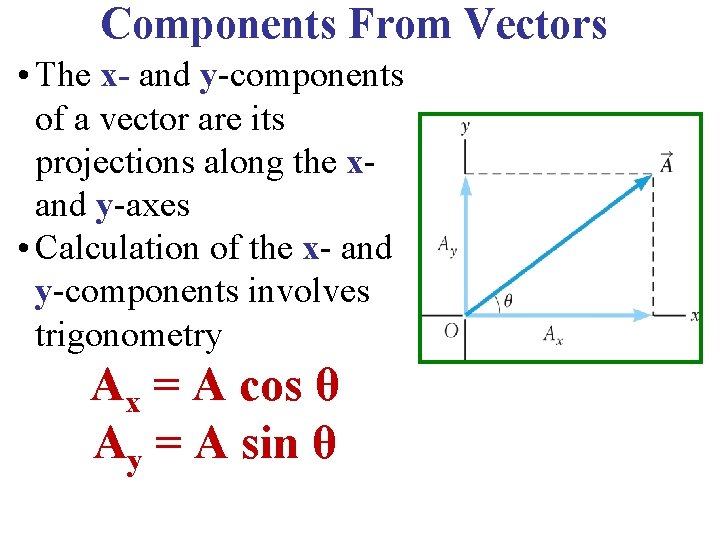
Components From Vectors • The x- and y-components of a vector are its projections along the xand y-axes • Calculation of the x- and y-components involves trigonometry Ax = A cos θ Ay = A sin θ

Vectors From Components • If we know the components, we can find the vector. • Use the Pythagorean Theorem for the magnitude: • Use the tan-1 function to find the direction:

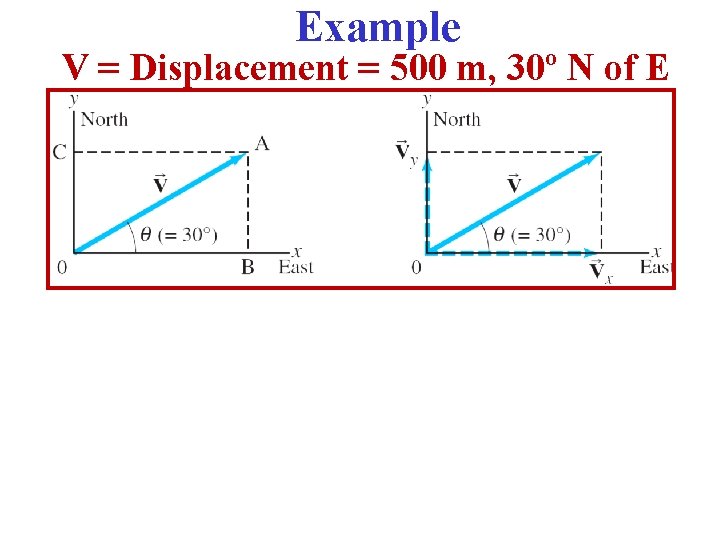
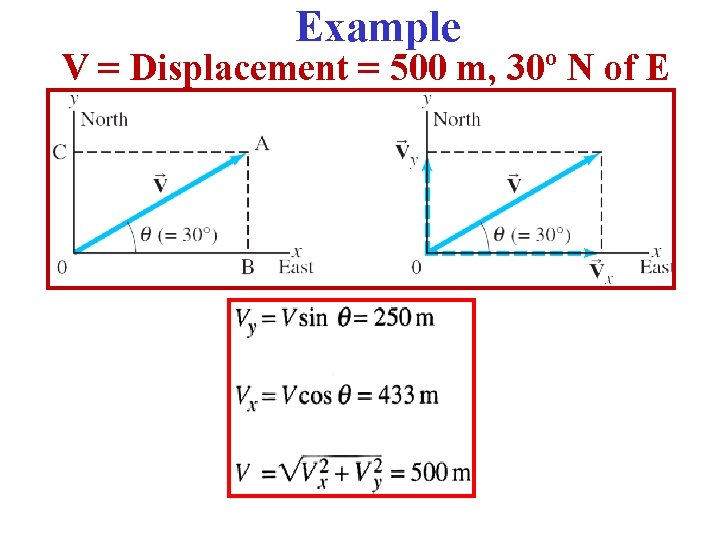
Example V = Displacement = 500 m, 30º N of E

Example V = Displacement = 500 m, 30º N of E

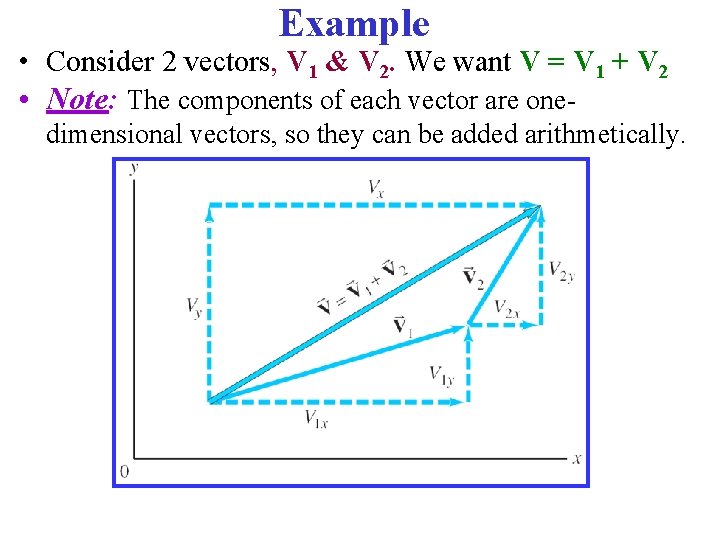
Example • Consider 2 vectors, V 1 & V 2. We want V = V 1 + V 2 • Note: The components of each vector are onedimensional vectors, so they can be added arithmetically.

We want the sum V = V 1 + V 2 “Recipe” for adding 2 vectors using trig & components: 1. Sketch a diagram to roughly add the vectors graphically. Choose x & y axes. 2. Resolve each vector into x & y components using sines & cosines. That is, find V 1 x, V 1 y, V 2 x, V 2 y. (V 1 x = V 1 cos θ 1, etc. ) 3. Add the components in each direction. (Vx = V 1 x + V 2 x, etc. ) 4. Find the length & direction of V by using:

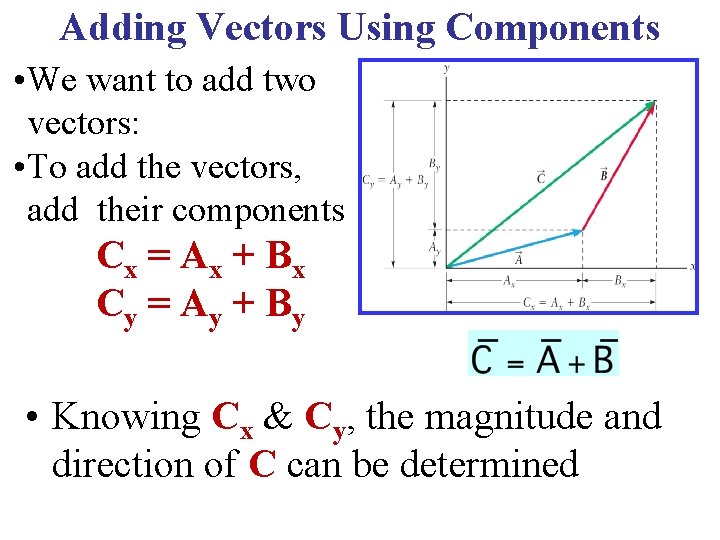
Adding Vectors Using Components • We want to add two vectors: • To add the vectors, add their components Cx = A x + B x Cy = A y + B y • Knowing Cx & Cy, the magnitude and direction of C can be determined

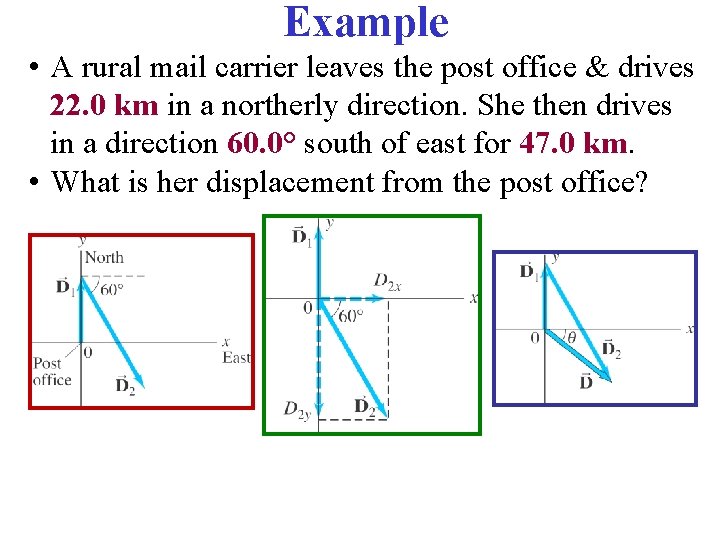
Example • A rural mail carrier leaves the post office & drives 22. 0 km in a northerly direction. She then drives in a direction 60. 0° south of east for 47. 0 km. • What is her displacement from the post office?

Solution, page 1 A rural mail carrier leaves the post office & drives 22. 0 km in a northerly direction. She then drives in a direction 60. 0° south of east for 47. 0 km. What is her displacement from the post office?

Solution, page 2 A rural mail carrier leaves the post office & drives 22. 0 km in a northerly direction. She then drives in a direction 60. 0° south of east for 47. 0 km. What is her displacement from the post office?

Example • A plane trip involves 3 legs, with 2 stopovers: 1) Due east for 620 km, 2) Southeast (45°) for 440 km, 3) 53° south of west, for 550 km. Calculate the plane’s total displacement.

Solution, Page 1 A plane trip involves 3 legs, with 2 stopovers: 1) Due east for 620 km, 2) Southeast (45°) for 440 km, 3) 53° south of west, for 550 km. Calculate the plane’s total displacement.

Solution, Page 2 A plane trip involves 3 legs, with 2 stopovers: 1) Due east for 620 km, 2) Southeast (45°) for 440 km, 3) 53° south of west, for 550 km. Calculate the plane’s total displacement.

Problem Solving You cannot solve a vector problem Without sketching a diagram!

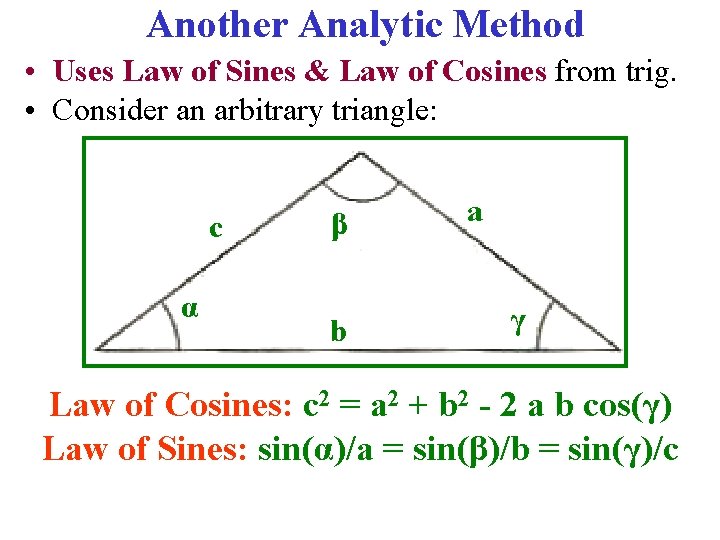
Another Analytic Method • Uses Law of Sines & Law of Cosines from trig. • Consider an arbitrary triangle: c α β b a γ Law of Cosines: c 2 = a 2 + b 2 - 2 a b cos(γ) Law of Sines: sin(α)/a = sin(β)/b = sin(γ)/c

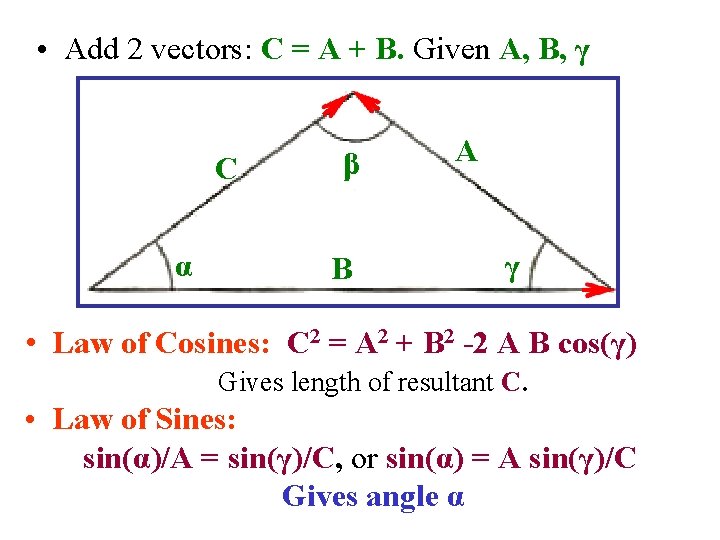
• Add 2 vectors: C = A + B. Given A, B, γ C α β B B A A γ • Law of Cosines: C 2 = A 2 + B 2 -2 A B cos(γ) Gives length of resultant C. • Law of Sines: sin(α)/A = sin(γ)/C, or sin(α) = A sin(γ)/C Gives angle α