Trigonometric Identities 1 of 10 Boardworks 2013 Information

Trigonometric Identities 1 of 10 © Boardworks 2013

Information 2 of 10 © Boardworks 2013

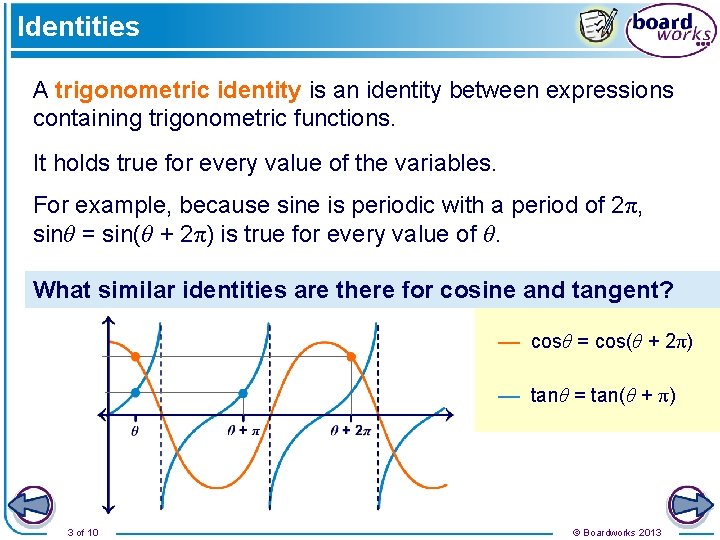
Identities A trigonometric identity is an identity between expressions containing trigonometric functions. It holds true for every value of the variables. For example, because sine is periodic with a period of 2π, sinθ = sin(θ + 2π) is true for every value of θ. What similar identities are there for cosine and tangent? –– cosθ = cos(θ + 2π) –– tanθ = tan(θ + π) 3 of 10 © Boardworks 2013

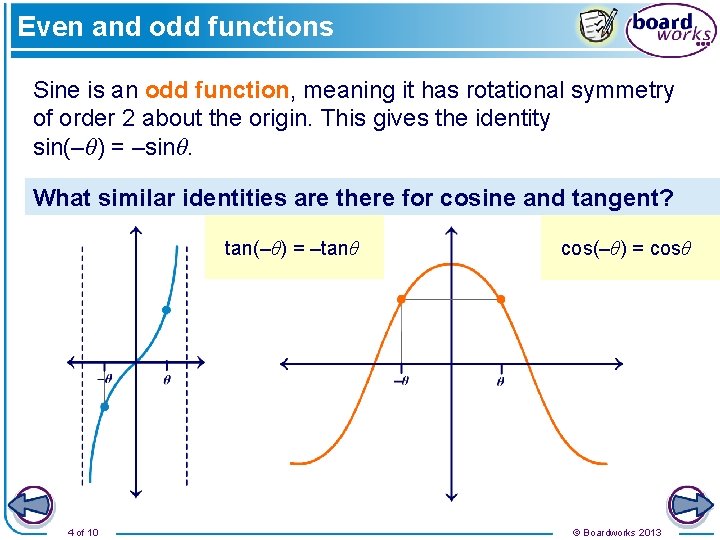
Even and odd functions Sine is an odd function, meaning it has rotational symmetry of order 2 about the origin. This gives the identity sin(–θ) = –sinθ. What similar identities are there for cosine and tangent? tan(–θ) = –tanθ 4 of 10 cos(–θ) = cosθ © Boardworks 2013

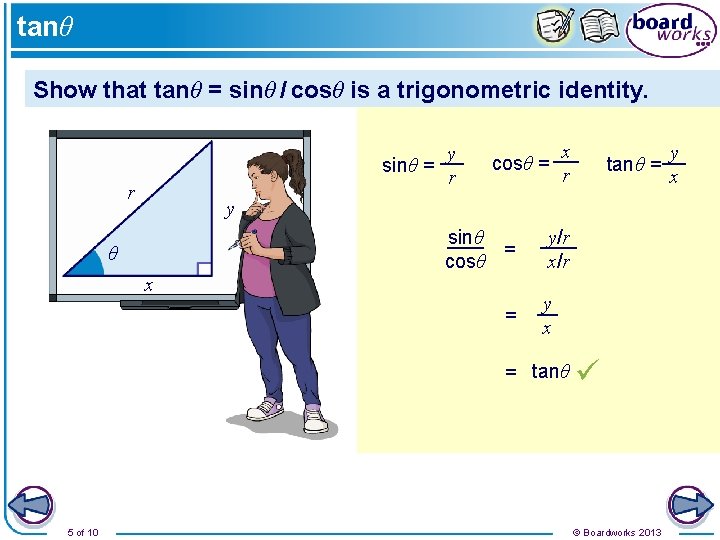
tanθ Show that tanθ = sinθ / cosθ is a trigonometric identity. sinθ = r y r cosθ = x r y sinθ = cosθ θ x = y/r x/r y x = tanθ 5 of 10 tanθ = © Boardworks 2013 y x

sin 2θ + cos 2θ Show that sin 2θ + cos 2θ = 1 is a trigonometric identity. y r sinθ = r y θ x x r cosθ = sin 2θ + cos 2θ = ( y r )2 + ( x r )2 x 2 + y 2 = r 2 Pythagorean theorem: x 2 + y 2 = r 2 sin 2θ + cos 2θ 2 r =1 6 of 10 © Boardworks 2013

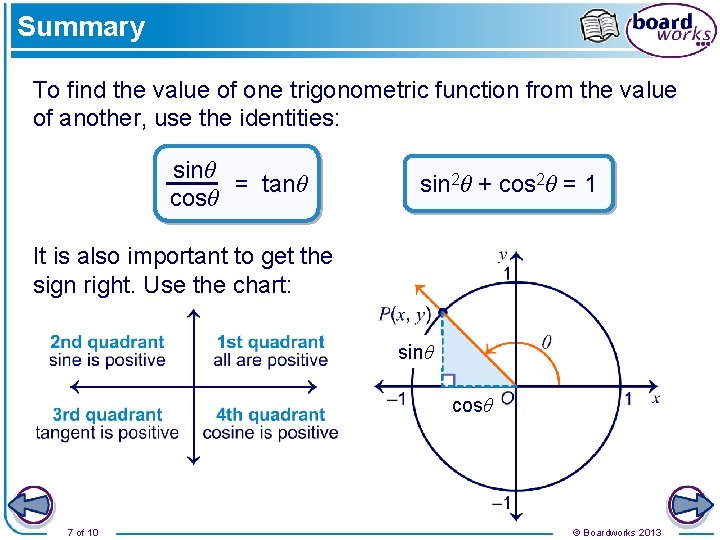
Summary To find the value of one trigonometric function from the value of another, use the identities: sinθ = tanθ cosθ sin 2θ + cos 2θ = 1 It is also important to get the sign right. Use the chart: sinθ cosθ 7 of 10 © Boardworks 2013

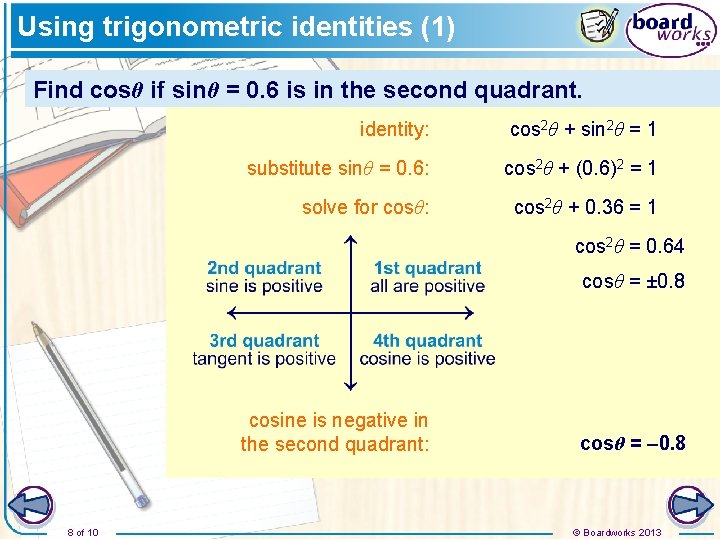
Using trigonometric identities (1) Find cosθ if sinθ = 0. 6 is in the second quadrant. identity: cos 2θ + sin 2θ = 1 substitute sinθ = 0. 6: cos 2θ + (0. 6)2 = 1 solve for cosθ: cos 2θ + 0. 36 = 1 cos 2θ = 0. 64 cosθ = ± 0. 8 cosine is negative in the second quadrant: 8 of 10 cosθ = – 0. 8 © Boardworks 2013

Using trigonometric identities (2) Find sinθ if tanθ = 0. 4 is in the fourth quadrant. identity: tanθ = sinθ cosθ substitute tanθ = 0. 4: 0. 4 = sinθ cosθ 0. 16 = sin 2θ cos 2θ square: substitute cos 2θ =1– sin 2θ: solve for sinθ: sin 2θ 0. 16 = 1 – sin 2θ = 0. 16(1 – sin 2θ) sin 2θ = 0. 16 – 0. 16 sin 2θ 1. 16 sin 2θ = 0. 16 sine is negative in the fourth quadrant: 9 of 10 sin 2θ = 0. 138 sinθ = – 0. 37 © Boardworks 2013