Trigonometric Functions Unit Circle Approach Radians vs Degrees

Radians vs. Degrees Measurements of common angles

Unit Circle Unit circle: Circle with radius 1 centered at the origin Equation: x

Unit Circle Travel t units around circle, starting from the point (1, 0), ending

Trigonometric Functions Let t be a real number and P = (x, y) the

Signs of the Trigonometric Functions ALL I STUDENTS II TAKE III CALCULUS IV

Exact Values Using Points on the Circle A point on the unit circle will

Exact Values Using Points on the Circle Example. Let t be a real number

Exact Values for Quadrantal Angles Example. Find the values of the trigonometric functions of

Exact Values for Quadrantal Angles Example. Find the exact values of (a) Problem: sin(90°)

Exact Values for Standard Angles Example. Find the values of the trigonometric functions of

Exact Values for Standard Angles Example. Find the values of the following expressions (a)

Circles of Radius r Theorem. For an angle θ in standard position, let P

Circles of Radius r Example. Problem: Find the exact values of each of the

Slides: 21

Download presentation

Trigonometric Functions: Unit Circle Approach

Radians vs. Degrees Measurements of common angles

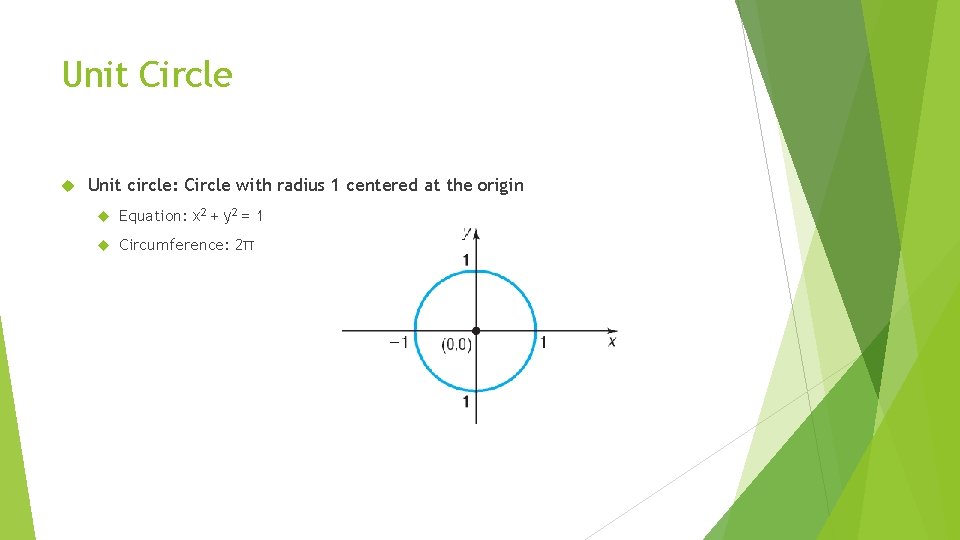
Unit Circle Unit circle: Circle with radius 1 centered at the origin Equation: x 2 + y 2 = 1 Circumference: 2π

Unit Circle Travel t units around circle, starting from the point (1, 0), ending at the point P = (x, y). Remember radians is the arc length in number of radii travelled as an angle rotates. The point P = (x, y) is used to define the trigonometric functions of t.

Trigonometric Functions Let t be a real number and P = (x, y) the point on the unit circle corresponding to t: Sine function: y-coordinate of P sin t = y Cosine function: x-coordinate of P cos t = x Tangent function: if x 0

Trigonometric Functions Let t be a real number and P = (x, y) the point on the unit circle corresponding to t: Cosecant function: if y 0 Secant function: if x 0 Cotangent function: if y 0

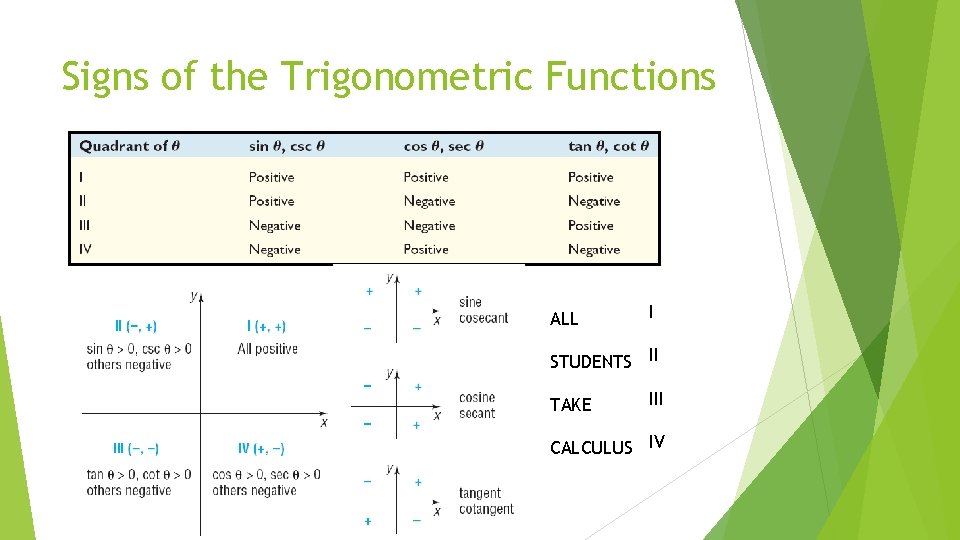
Signs of the Trigonometric Functions ALL I STUDENTS II TAKE III CALCULUS IV

Exact Values Using Points on the Circle A point on the unit circle will satisfy the equation x 2 + y 2 = 1 Use this information together with the definitions of the trigonometric functions.

Exact Values Using Points on the Circle Example. Let t be a real number and P = circle that corresponds to t. the point on the unit Problem: Find the values of sin t, cos t, tan t, csc t, sec t and cot t

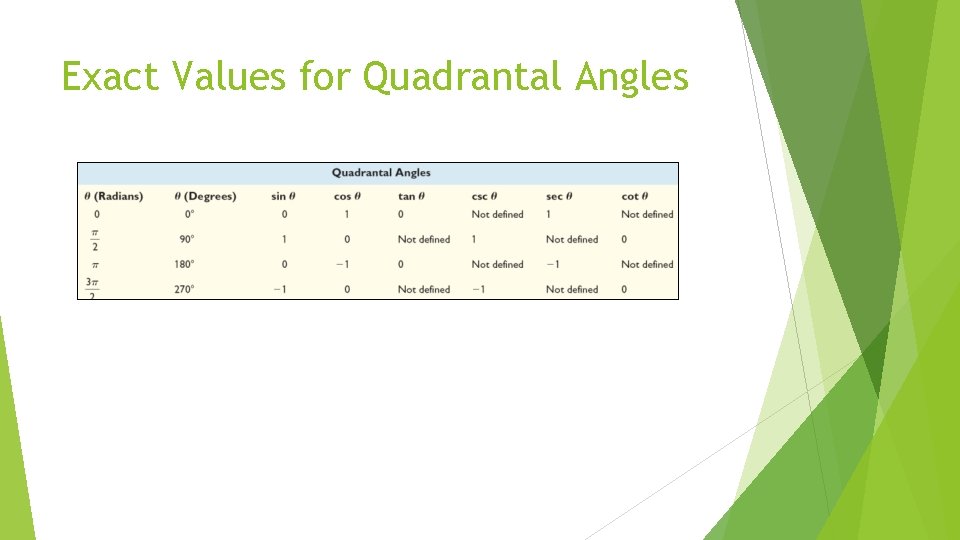
Exact Values for Quadrantal Angles Example. Find the values of the trigonometric functions of θ Problem: θ = = 90°

Exact Values for Quadrantal Angles Example. Find the values of the trigonometric functions of θ Problem: θ = π = 180°

Exact Values for Quadrantal Angles Example. Find the values of the trigonometric functions of θ Problem: θ= = 270°

Exact Values for Quadrantal Angles

Exact Values for Quadrantal Angles Example. Find the exact values of (a) Problem: sin(90°) (b) Problem: cos(5π)

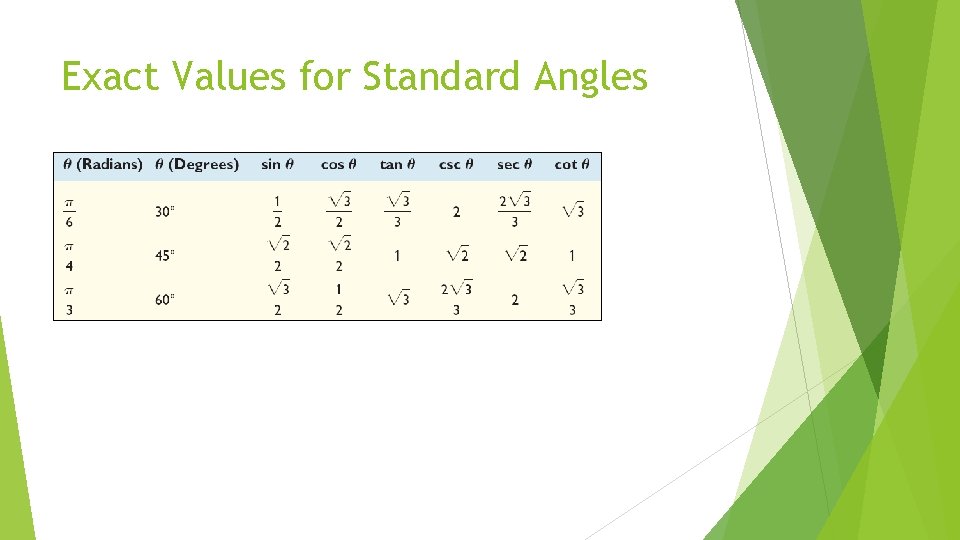
Exact Values for Standard Angles Example. Find the values of the trigonometric functions of θ Problem: θ = = 45°

Exact Values for Standard Angles Example. Find the values of the trigonometric functions of θ Problem: θ = = 60°

Exact Values for Standard Angles Example. Find the values of the trigonometric functions of θ Problem: θ = = 30°

Exact Values for Standard Angles

Exact Values for Standard Angles Example. Find the values of the following expressions (a) Problem: sin(315°) (b) Problem: cos(120°) (c) Problem:

Circles of Radius r Theorem. For an angle θ in standard position, let P = (x, y) be the point on the terminal side of θ that is also on the circle x 2 + y 2 = r 2. Then

Circles of Radius r Example. Problem: Find the exact values of each of the trigonometric functions of an angle µ if (-12, -5) is a point on its terminal side.