Trigonometric Functions The Unit Circle Section 4 2

Trigonometric Functions: The Unit Circle Section 4. 2

Objectives • Identify a unit circle and describe its relationship to real numbers. • Evaluate trigonometric functions using the unit circle. • Recognize the domain and range of sine and cosine functions • Find the exact values of the trig functions at /4 • Use even and odd trig functions • Recognize and use fundamental identities • Periodic functions

Trigonometric Ratios • The word trigonometry originates from two Greek terms, trigon, which means triangle, and metron, which means measure. Thus, the study of trigonometry is the study of triangle measurements. • A ratio of the lengths of the sides of a right triangle is called a trigonometric ratio. The three most common trigonometric ratios are sine, cosine, and tangent.

Trigonometric Ratios Only Apply to Right Triangles

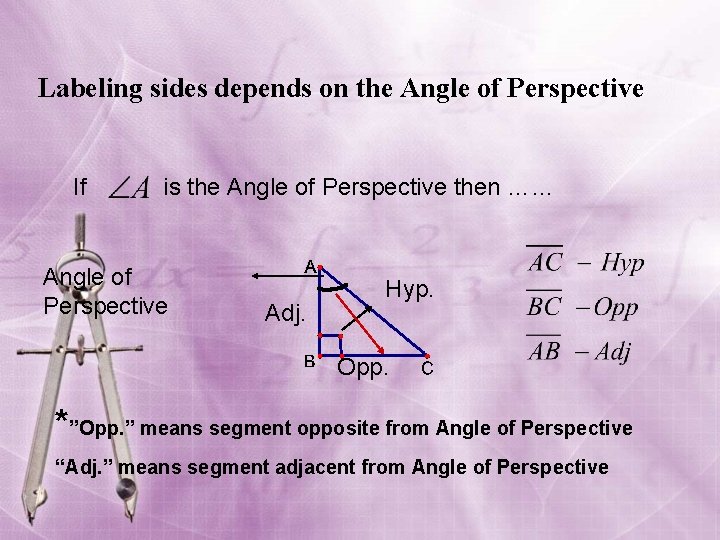
In right triangles : • The segment across from the right angle ( ) is labeled the hypotenuse “Hyp. ”. Hyp. Opp. Angle of Perspective Adj. • The “angle of perspective” determines how to label the sides. • Segment opposite from the Angle of Perspective( ) is labeled “Opp. ” • Segment adjacent to (next to) the Angle of Perspective ( ) is labeled “Adj. ”. * The angle of Perspective is never the right angle.

Labeling sides depends on the Angle of Perspective If is the Angle of Perspective then …… Angle of Perspective Adj. Hyp. Opp. *”Opp. ” means segment opposite from Angle of Perspective “Adj. ” means segment adjacent from Angle of Perspective

If the Angle of Perspective is then Adj Hyp then Opp Hyp Adj

The 3 Trigonometric Ratios • The 3 ratios are Sine, Cosine and Tangent

The Amazing Legend of… Chief Soh. Cah. Toa

Chief Soh. Cah. Toa • Once upon a time there was a wise old Native American Chief named Chief Soh. Cah. Toa. • He was named that due to a chance encounter with his coffee table in the middle of the night. • He woke up hungry, got up and headed to the kitchen to get a snack. • He did not turn on the light and in the darkness, stubbed his big toe on his coffee table…. Please share this story with Mr. Gustin for historical credibility.

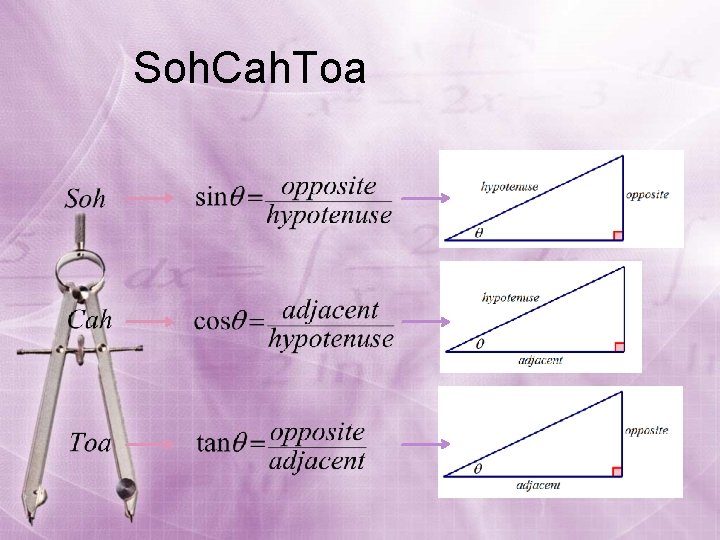
Trigonometric Ratios To help you remember these A trigonometric relationships, Sin A = Opposite side SOH you can use the mnemonic Hypotenuse Cos A = Adjacent side CAH device, SOH-CAH-TOA, Hypotenuse b where the first letter of Tan A = Opposite side TOA Adjacent side each word of the trigonometric ratios is represented in the correct C order. c a B

Soh. Cah. Toa

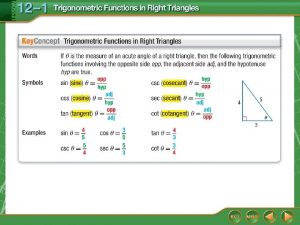
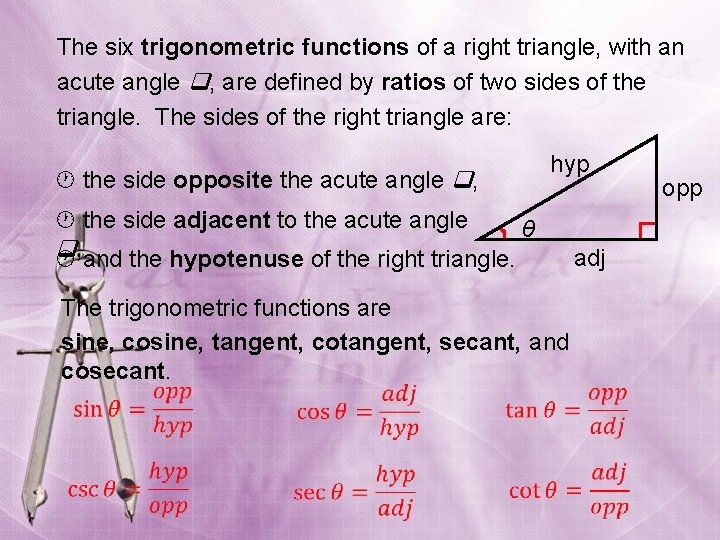
The six trigonometric functions of a right triangle, with an acute angle , are defined by ratios of two sides of the triangle. The sides of the right triangle are: hyp the side opposite the acute angle , the side adjacent to the acute angle θ , and the hypotenuse of the right triangle. adj The trigonometric functions are sine, cosine, tangent, cotangent, secant, and cosecant. opp

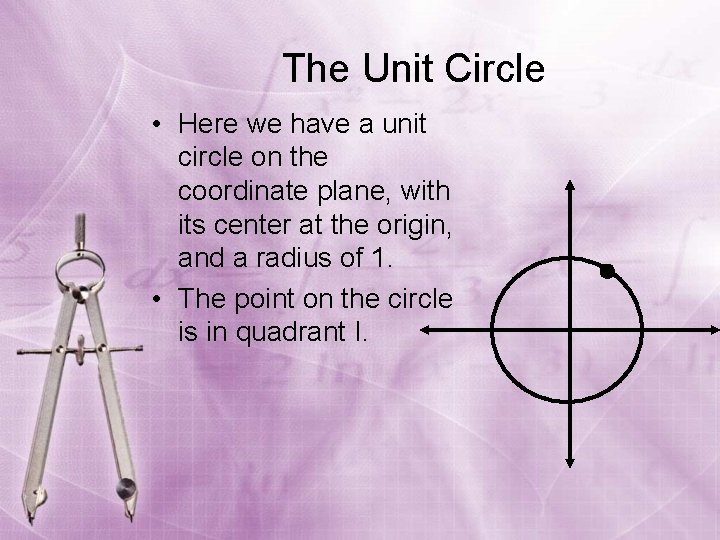
The Unit Circle • Here we have a unit circle on the coordinate plane, with its center at the origin, and a radius of 1. • The point on the circle is in quadrant I.

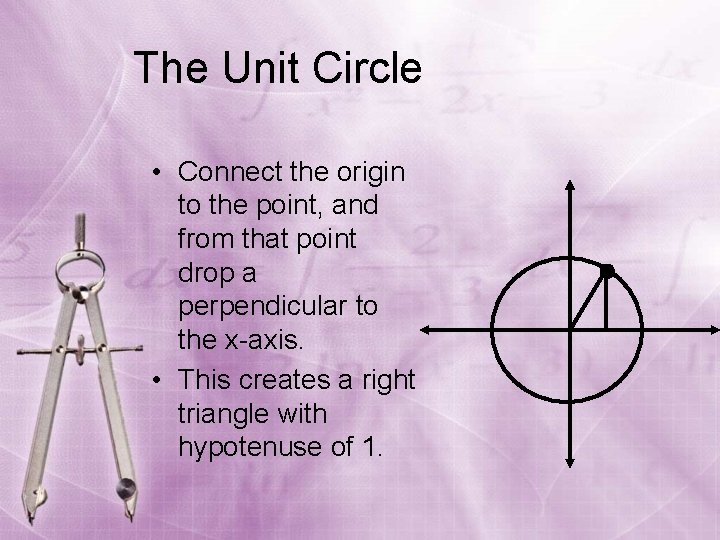
The Unit Circle • Connect the origin to the point, and from that point drop a perpendicular to the x-axis. • This creates a right triangle with hypotenuse of 1.

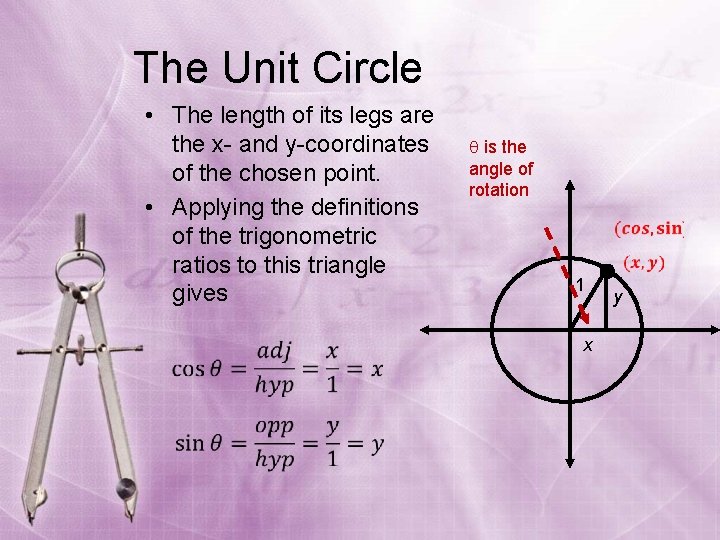
The Unit Circle • The length of its legs are the x- and y-coordinates of the chosen point. • Applying the definitions of the trigonometric ratios to this triangle gives is the angle of rotation 1 x y

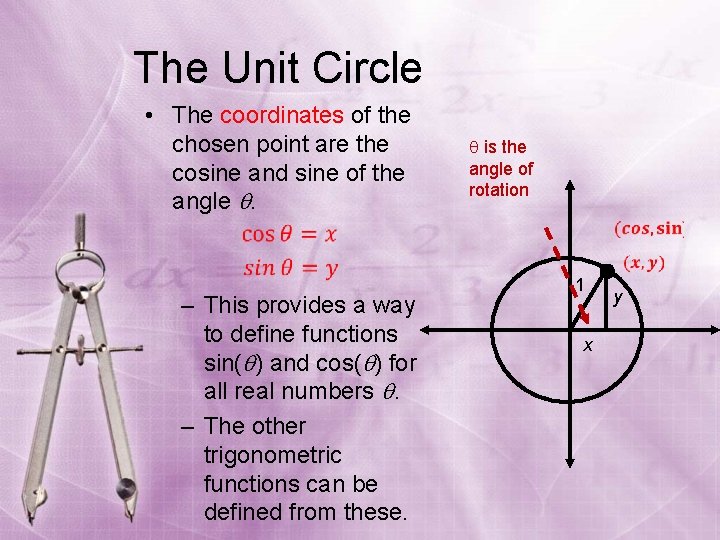
The Unit Circle • The coordinates of the chosen point are the cosine and sine of the angle . is the angle of rotation – This provides a way to define functions sin( ) and cos( ) for all real numbers . – The other trigonometric functions can be defined from these. 1 x y

Trigonometric Functions is the angle of rotation 1 x These functions are reciprocals of each other. y

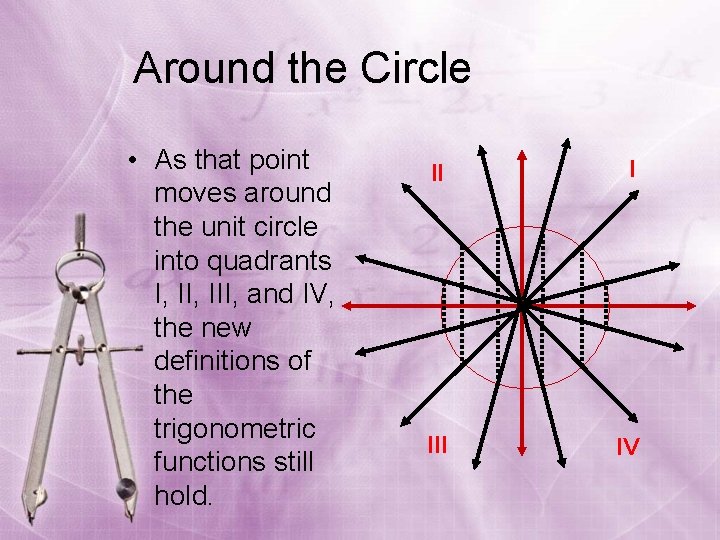
Around the Circle • As that point moves around the unit circle into quadrants I, III, and IV, the new definitions of the trigonometric functions still hold. II I III IV

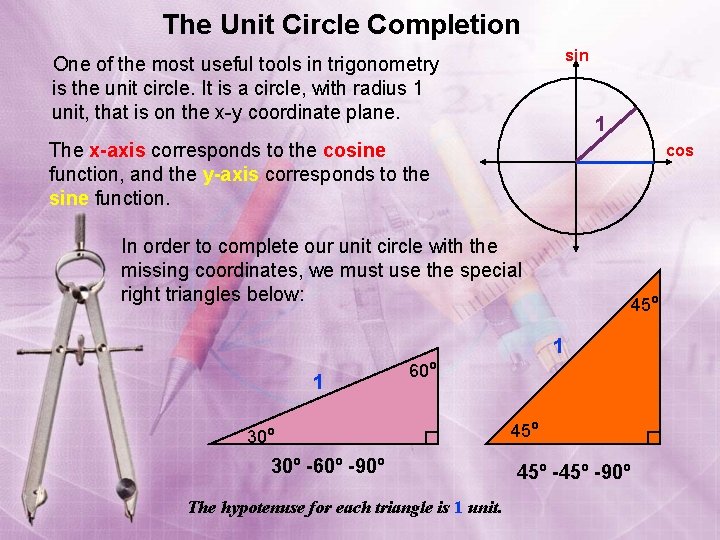
The Unit Circle Completion sin One of the most useful tools in trigonometry is the unit circle. It is a circle, with radius 1 unit, that is on the x-y coordinate plane. 1 The x-axis corresponds to the cosine function, and the y-axis corresponds to the sine function. cos In order to complete our unit circle with the missing coordinates, we must use the special right triangles below: 45º 1 1 60º 30º -60º -90º The hypotenuse for each triangle is 1 unit. 45º -45º -90º

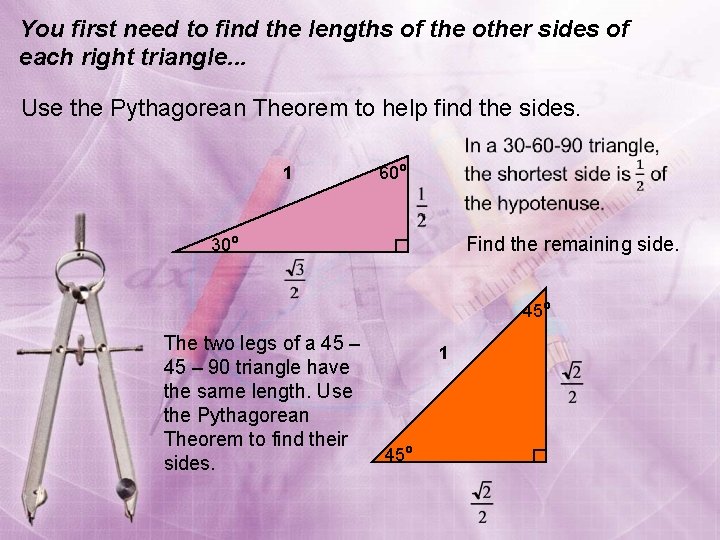
You first need to find the lengths of the other sides of each right triangle. . . Use the Pythagorean Theorem to help find the sides. 1 60º 30º Find the remaining side. 45º The two legs of a 45 – 90 triangle have the same length. Use the Pythagorean Theorem to find their 45º sides. 1

Usefulness of Knowing Trigonometric Functions of Special Angles: 30 o, 45 o, 60 o • The trigonometric function values derived from knowing the side ratios of the 30 -60 -90 and 45 -4590 triangles are “exact” numbers, not decimal approximations as could be obtained from using a calculator • You will often be asked to find exact trig function values for angles other than 30 o, 45 o and 60 o angles that are somehow related to trig function values of these angles

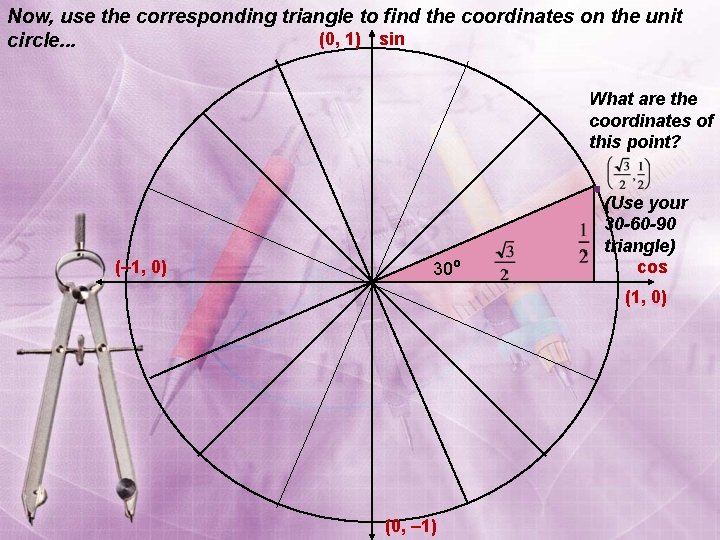
Now, use the corresponding triangle to find the coordinates on the unit (0, 1) sin circle. . . What are the coordinates of this point? (– 1, 0) 30º (Use your 30 -60 -90 triangle) cos (1, 0) (0, – 1)

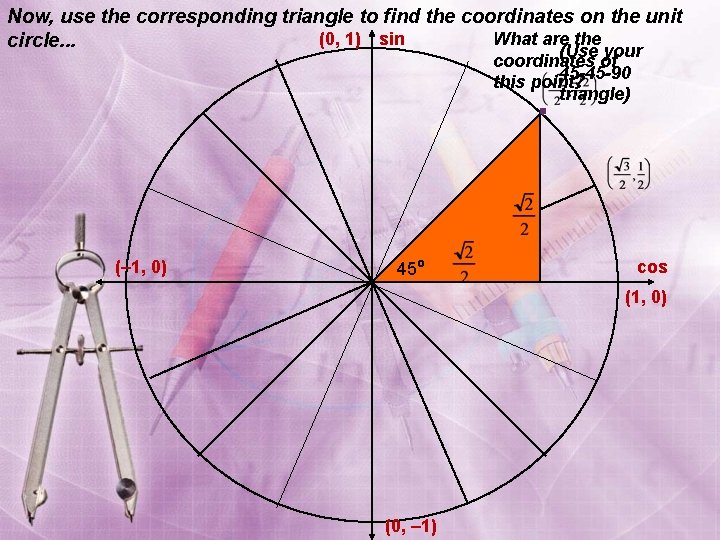
Now, use the corresponding triangle to find the coordinates on the unit What are the (0, 1) sin circle. . . (Use your coordinates of 45 -45 -90 this point? triangle) (– 1, 0) 45º cos (1, 0) (0, – 1)

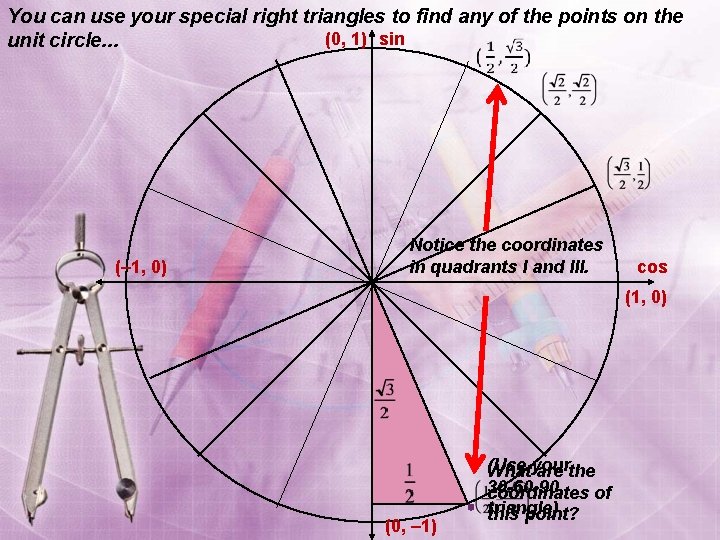
You can use your special right triangles to find any of the points on the (0, 1) sin unit circle. . . (Use your 30 -60 -90 triangle) What are the coordinates of this point? (– 1, 0) cos (1, 0) (0, – 1)

You can use your special right triangles to find any of the points on the (0, 1) sin unit circle. . . (– 1, 0) Notice the coordinates in quadrants I and III. cos (1, 0) (0, – 1) (Use Whatyour are the 30 -60 -90 coordinates of triangle) this point?

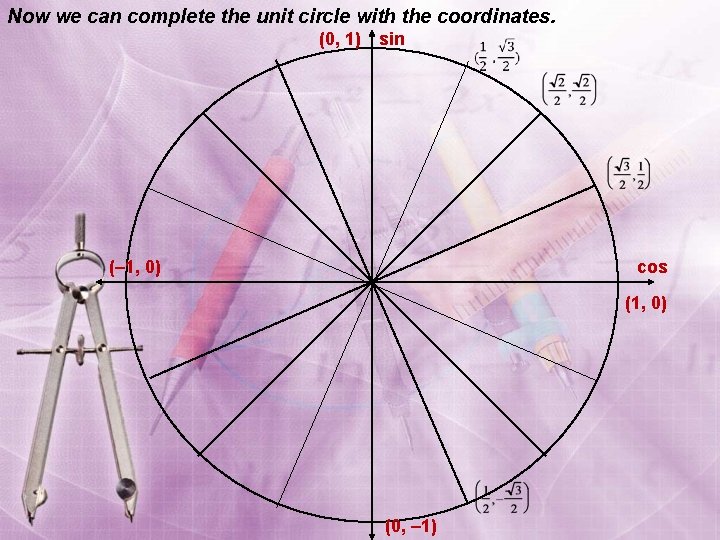
Now we can complete the unit circle with the coordinates. (0, 1) sin (– 1, 0) cos (1, 0) (0, – 1)

Let’s look at a quick way to get the coordinates (in-class only) (0, 1) (– 1, 0) (0, – 1)

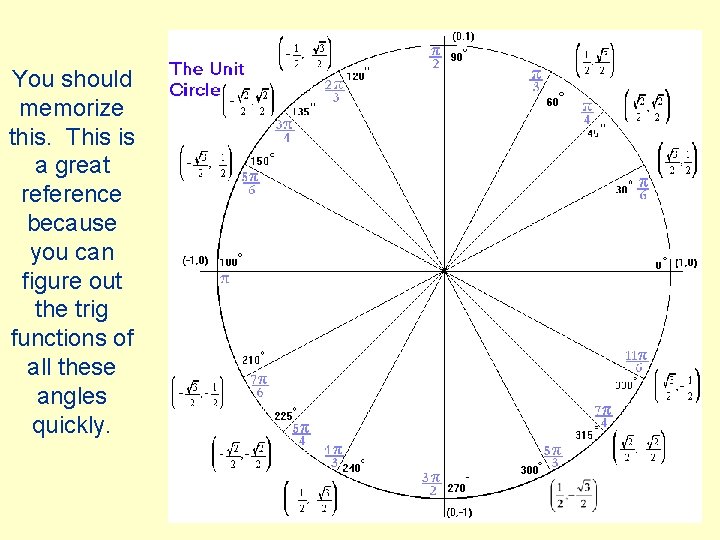
You should memorize this. This is a great reference because you can figure out the trig functions of all these angles quickly.

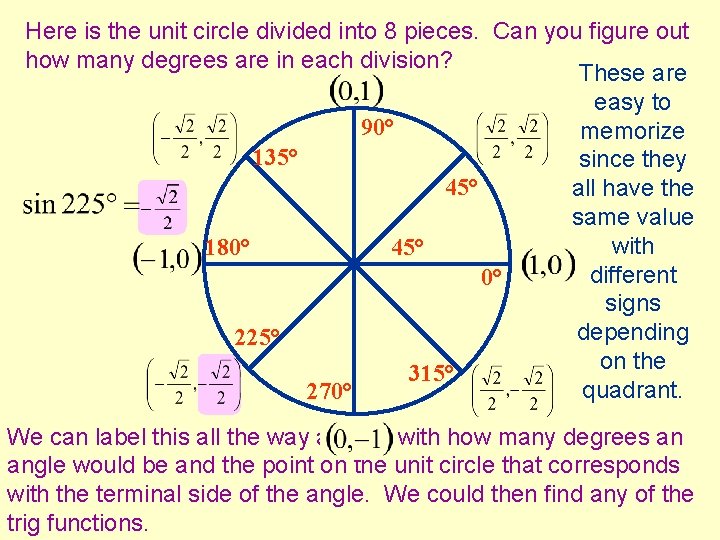
Here is the unit circle divided into 8 pieces. Can you figure out how many degrees are in each division? These are easy to 90° memorize 135° since they 45° all have the same value with 180° 45° different 0° signs depending 225° on the 315° quadrant. 270° We can label this all the way around with how many degrees an angle would be and the point on the unit circle that corresponds with the terminal side of the angle. We could then find any of the trig functions.

Can you figure out what these angles would be in radians? 90° 135° 45° 180° 0° 225° 270° 315° The circle is 2 all the way around so half way is . The upper half is divided into 4 pieces so each piece is /4.

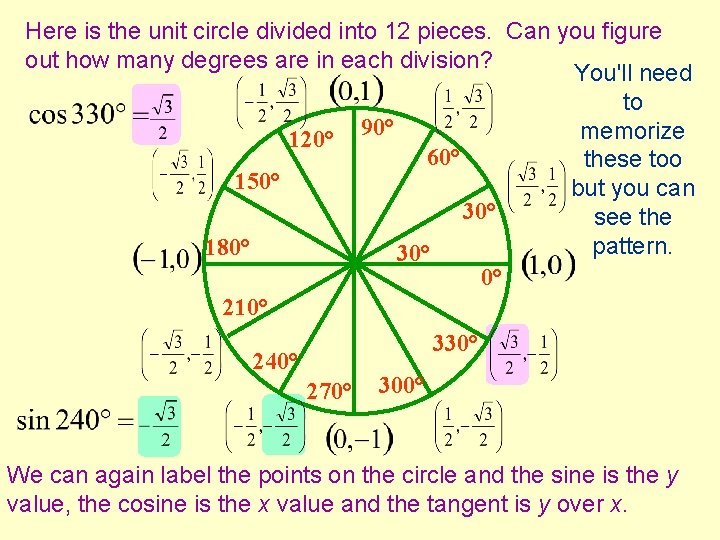
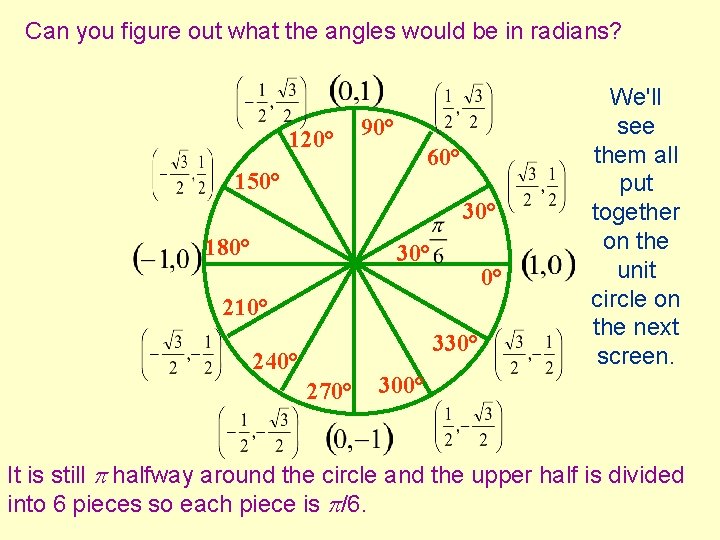
Here is the unit circle divided into 12 pieces. Can you figure out how many degrees are in each division? You'll need to memorize 120° 90° 60° these too 150° but you can 30° see the pattern. 180° 30° 0° 210° 330° 240° 270° 300° We can again label the points on the circle and the sine is the y value, the cosine is the x value and the tangent is y over x.

Can you figure out what the angles would be in radians? 120° 90° 60° 150° 30° 180° 30° 0° 210° 330° 240° 270° We'll see them all put together on the unit circle on the next screen. 300° It is still halfway around the circle and the upper half is divided into 6 pieces so each piece is /6.

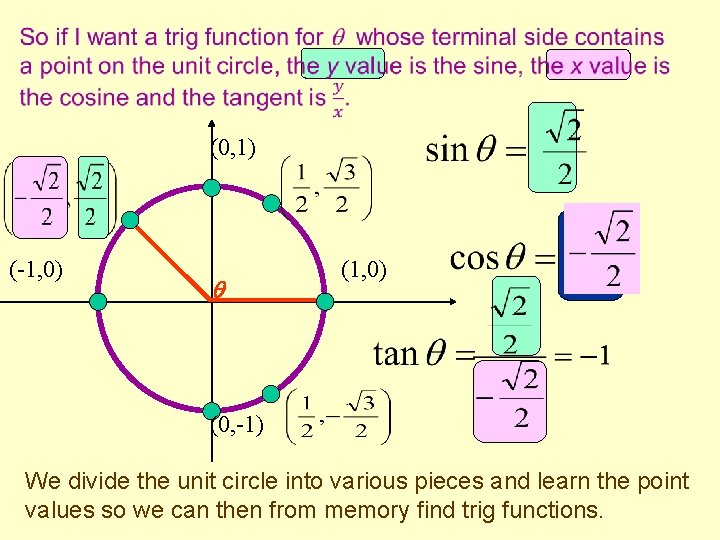
(0, 1) (-1, 0) (0, -1) We divide the unit circle into various pieces and learn the point values so we can then from memory find trig functions.

We know all of the sides of this triangle. The bottom leg is just the x value of the point, the other leg is just the y value and the hypotenuse is always 1 because it is a radius of the unit circle. (0, 1) (-1, 0) (0, -1) Notice the sine is just the y value of the unit circle point and the cosine is just the x value.

Finding Values of the Trigonometric Functions What are the coordinates?

Finding Values of the Trigonometric Functions What are the coordinates?

Let’s look at an applet. http: //www. analyzemath. com/unitcircle/unit_circle_applet. ht ml What is the domain of sine and cosine? All real numbers What is the range of sine and cosine?

Even and Odd Trig Functions

This is an even function. Think “same as”. Remember negative angle means to go clockwise

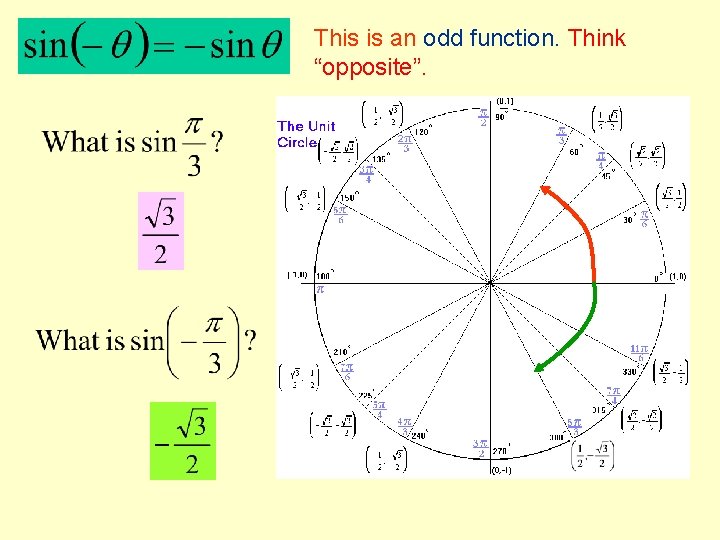
This is an odd function. Think “opposite”.

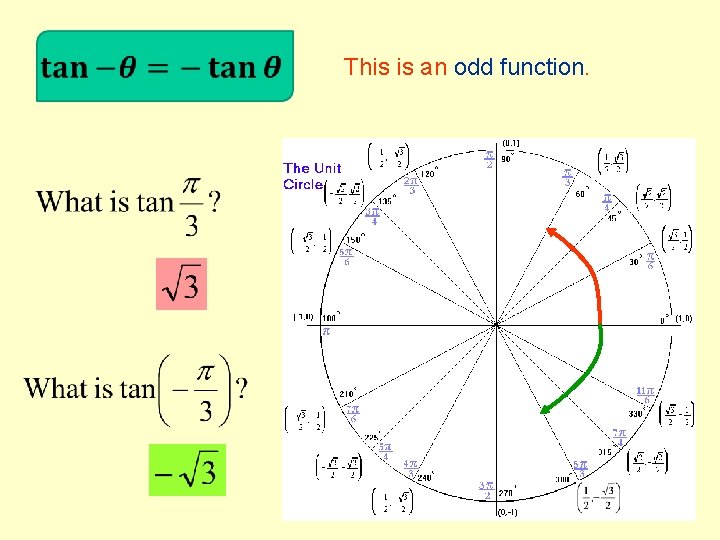
This is an odd function.

Using Even and Odd Functions to Find Values of Trig Functions

Using Even and Odd Functions to Find Values of Trig Functions

Reciprocal Identities

Quotient Identities

Using Quotient and Reciprocal Identities

Using Quotient and Reciprocal Identities

Using Quotient and Reciprocal Identities

Using Quotient and Reciprocal Identities

Pythagorean Identities

Pythagorean Identities

Pythagorean Identities

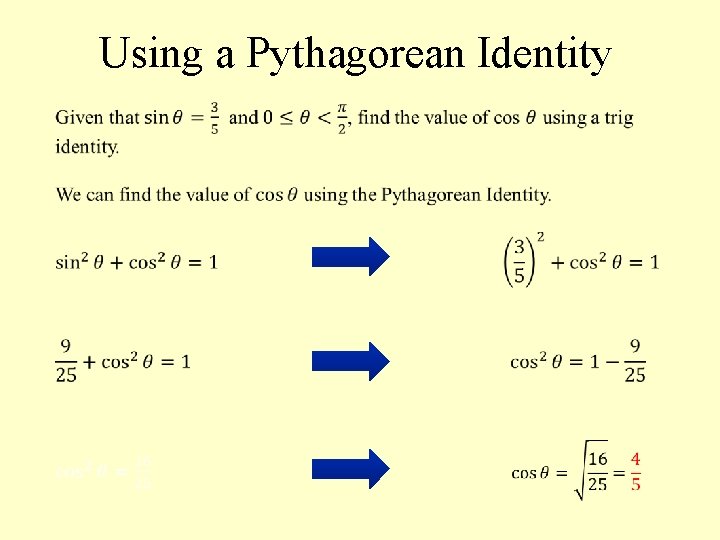
Using a Pythagorean Identity

Periodic Functions

Periodic Properties of the Sine and Cosine Functions

Periodic Properties of the Tangent and Cotangent Functions

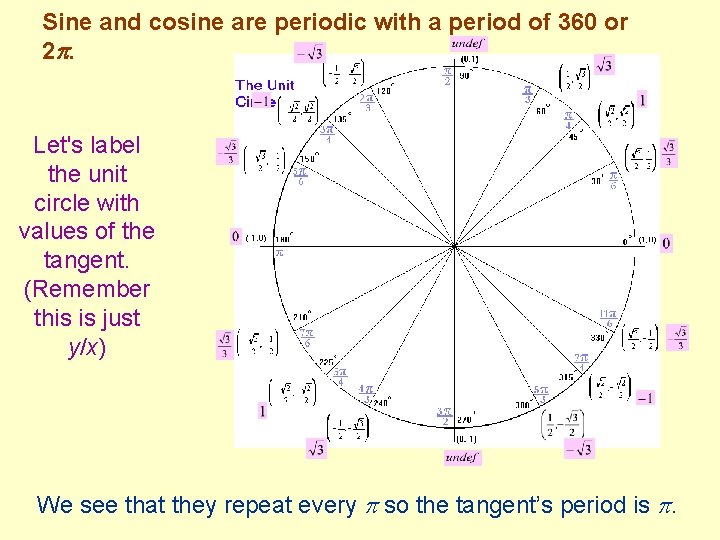
Sine and cosine are periodic with a period of 360 or 2 . Let's label the unit circle with values of the tangent. (Remember this is just y/x) We see that they repeat every so the tangent’s period is .

Reciprocal functions have the same period. PERIODIC PROPERTIES sin( + 2 ) = sin csc( + 2 ) = csc cos( + 2 ) = cos sec( + 2 ) = sec tan( + ) = tan cot( + ) = cot 1 This would have the same value as (you can count around on unit circle or subtract the period twice. )

EXAMPLES: Evaluate the trigonometric function using its period as an aid

EXAMPLES: Evaluate the trigonometric function using its period as an aid