Trigonometric Functions Right Triangle Approach Copyright Cengage Learning

Trigonometric Functions: Right Triangle Approach Copyright © Cengage Learning. All rights reserved.

6. 1 Angle Measure Copyright © Cengage Learning. All rights reserved.

Objectives ► Angle Measure ► Angles in Standard Position ► Length of a Circular Arc ► Area of a Circular Sector ► Circular Motion 3

Angle Measure An angle AOB consists of two rays R 1 and R 2 with a common vertex O (see Figure 1). We often interpret an angle as a rotation of the ray R 1 onto R 2. Negative angle Positive angle Figure 1 4

Angle Measure In this case, R 1 is called the initial side, and R 2 is called the terminal side of the angle. If the rotation is counterclockwise, the angle is considered positive, and if the rotation is clockwise, the angle is considered negative. 5

Angle Measure The measure of an angle is the amount of rotation about the vertex required to move R 1 onto R 2. Intuitively, this is how much the angle “opens. ” One unit of measurement for angles is the degree. An angle of measure 1 degree is formed by rotating the initial side of a complete revolution. In calculus and other branches of mathematics, a more natural method of measuring angles is used—radian measure. 6

Angle Measure hjdf Figure 2 7

Angle Measure The circumference of the circle of radius 1 is 2 and so a complete revolution has measure 2 rad, a straight angle has measure rad, and a right angle has measure /2 rad. An angle that is subtended by an arc of length 2 along the unit circle has radian measure 2 (see Figure 3). Radian measure Figure 3 8

Angle Measure 9

Example 1 – Converting Between Radians and Degrees (a) Express 60 in radians. (b) Express rad in degrees. Solution: The relationship between degrees and radians gives (a) 60 (b) = 30 10

Angle Measure A note on terminology: We often use a phrase such as “a 30 angle” to mean an angle whose measure is 30. Also, for an angle , we write = 30 or = /6 to mean the measure of is 30 or /6 rad. When no unit is given, the angle is assumed to be measured in radians. 11

Angles in Standard Position 12

Angles in Standard Position An angle is in standard position if it is drawn in the xy-plane with its vertex at the origin and its initial side on the positive x-axis. Figure 5 gives examples of angles in standard position. (a) (b) (c) (d) Angles in standard position Figure 5 13

Angles (continued) An angle is called a quadrantal angle if its terminal side lies on the x-axis or on the y-axis. Angle is an example of a quadrantal angle. 14

Drawing Angles in Standard Position The figure illustrates that when the terminal side makes one full revolution, it forms an angle whose radian measure is The figure shows the quadrantal angles formed by 3/4, 1/2, and 1/4 of a revolution. 15

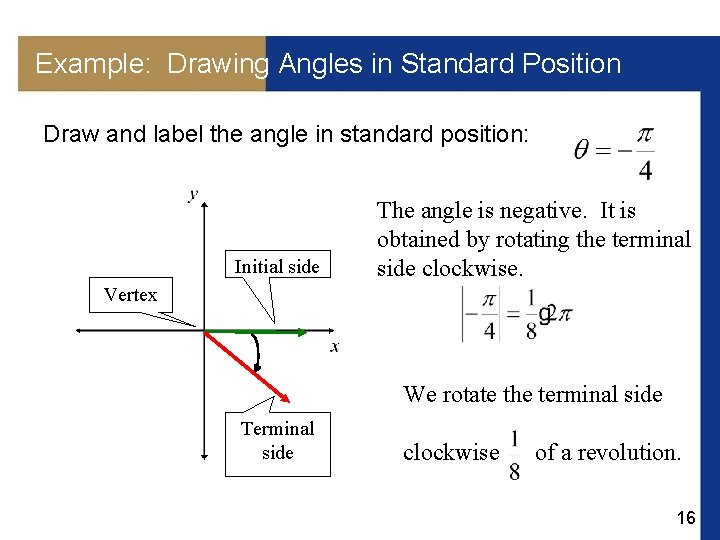
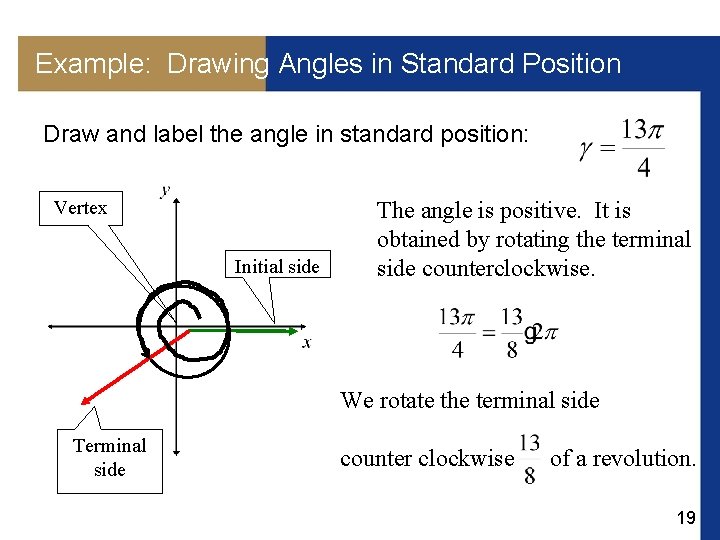
Example: Drawing Angles in Standard Position Draw and label the angle in standard position: Initial side The angle is negative. It is obtained by rotating the terminal side clockwise. Vertex We rotate the terminal side Terminal side clockwise of a revolution. 16

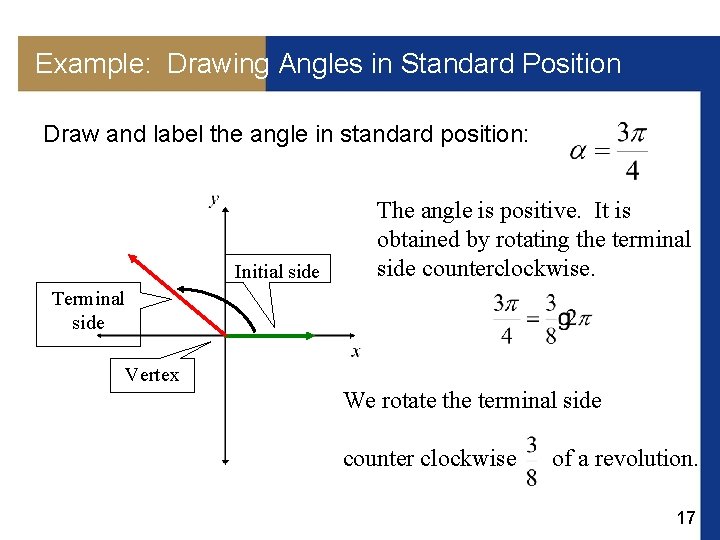
Example: Drawing Angles in Standard Position Draw and label the angle in standard position: Initial side The angle is positive. It is obtained by rotating the terminal side counterclockwise. Terminal side Vertex We rotate the terminal side counter clockwise of a revolution. 17

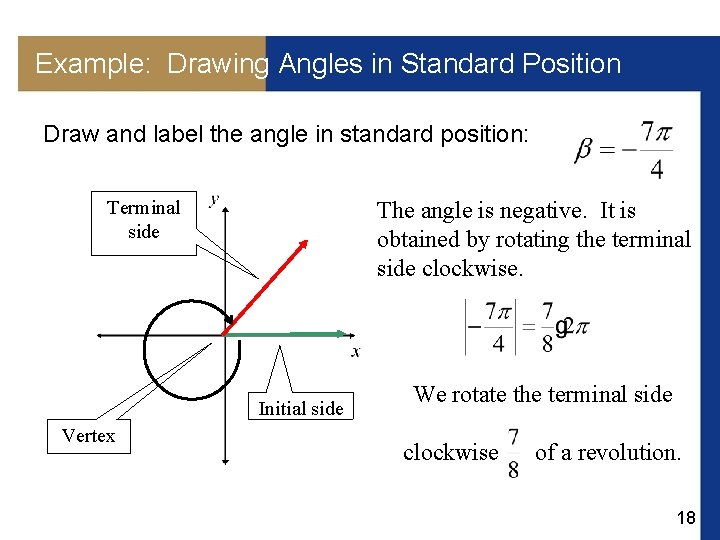
Example: Drawing Angles in Standard Position Draw and label the angle in standard position: Terminal side The angle is negative. It is obtained by rotating the terminal side clockwise. Initial side Vertex We rotate the terminal side clockwise of a revolution. 18

Example: Drawing Angles in Standard Position Draw and label the angle in standard position: Vertex Initial side The angle is positive. It is obtained by rotating the terminal side counterclockwise. We rotate the terminal side Terminal side counter clockwise of a revolution. 19

20

21

22

23

Angles are commonly measured in either 1) Degrees 2) Radians 3) Revolutions (or Rotations) 4) Degrees, Minutes, Seconds 24

Angles in Standard Position Two angles in standard position are coterminal if their sides coincide. In other words, two angles with the same initial and terminal sides but possibly different rotations are called coterminal angles. In Figure 5 the angles in (a) and (c) are coterminal. 25

Finding Coterminal Angles 26

Example 2 – Coterminal Angles (a) Find angles that are coterminal with the angle = 30 in standard position. (b) Find angles that are coterminal with the angle = in standard position. Solution: (a) To find positive angles that are coterminal with , we add any multiple of 360. 27

Example 2 – Solution cont’d Thus 30° + 360° = 390° and 30° + 720° = 750° are coterminal with = 30. To find negative angles that are coterminal with , we subtract any multiple of 360°. Thus 30° – 360° = – 330° and 30° – 720° = – 690° are coterminal with . 28

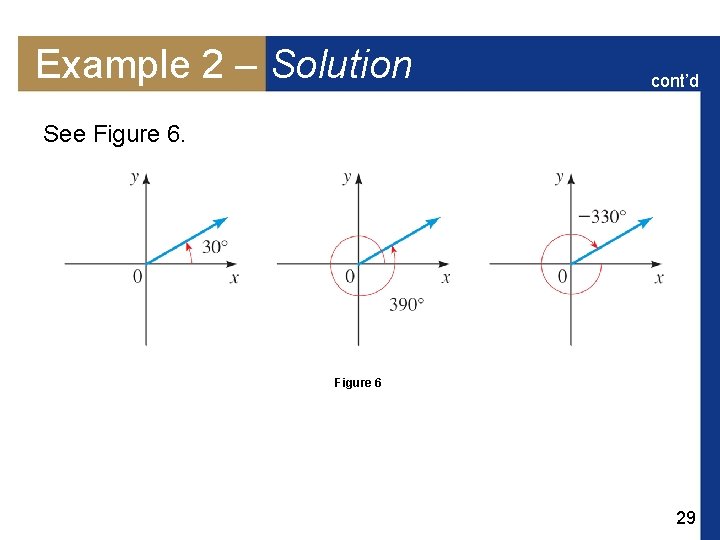
Example 2 – Solution cont’d See Figure 6 29

Example 2 – Solution cont’d (b) To find positive angles that are coterminal with , we add any multiple of 2. Thus and are coterminal with = /3. To find negative angles that are coterminal with , we subtract any multiple of 2. 30

Example 2 – Solution cont’d Thus and are coterminal with = /3. To find negative angles that are coterminal with , we subtract any multiple of 2. 31

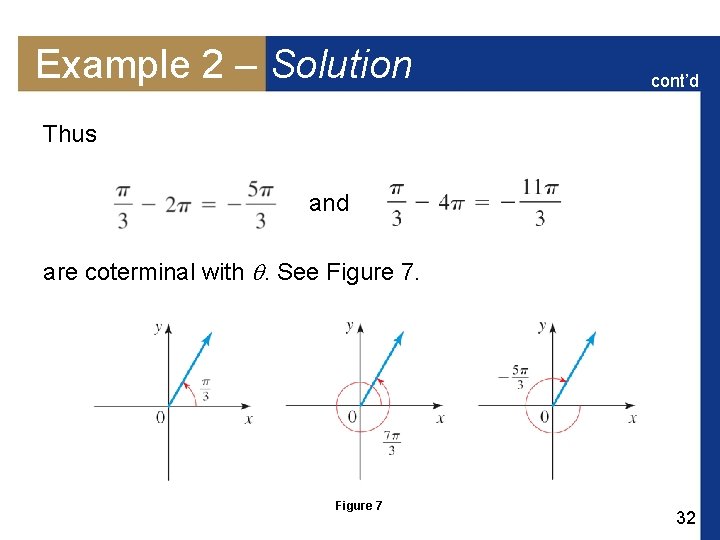
Example 2 – Solution cont’d Thus and are coterminal with . See Figure 7 32

Example 3 – Coterminal Angles 33

Length of a Circular Arc 34

Length of a Circular Arc Solving for , we get the important formula 35

Length of a Circular Arc This formula allows us to define radian measure using a circle of any radius r : The radian measure of an angle is s/r, where s is the length of the circular arc that subtends in a circle of radius r (see Figure 10). The radian measure of is the number of “radiuses” that can fit in the arc that subtends ; hence the term radian. Figure 10 36

Example 4 – Arc Length and Angle Measure (a) Find the length of an arc of a circle with radius 10 m that subtends a central angle of 30. (b) A central angle in a circle of radius 4 m is subtended by an arc of length 6 m. Find the measure of in radians. Solution: (a) From Example 1(b) we see that 30 = /6 rad. So the length of the arc is s = r = = 37

Example 4 – Solution cont’d (b) By the formula = s/r, we have 38

Area of a Circular Sector 39

Area of a Circular Sector 40

Example 5 – Area of a Sector Find the area of a sector of a circle with central angle 60 if the radius of the circle is 3 m. Solution: To use the formula for the area of a circular sector, we must find the central angle of the sector in radians: 60° = 60( /180) rad = /3 rad. Thus, the area of the sector is 41

Circular Motion 42

Circular Motion Suppose a point moves along a circle as shown in Figure 12. There are two ways to describe the motion of the point: linear speed angular speed. Linear speed is the rate at which the distance traveled is changing, so linear speed is the distance traveled divided by the time elapsed. Figure 12 43

Circular Motion Angular speed is the rate at which the central angle is changing, so angular speed is the number of radians this angle changes divided by the time elapsed. 44

Example 6 – Finding Linear and Angular Speed A boy rotates a stone in a 3 -ft-long sling at the rate of 15 revolutions every 10 seconds. Find the angular and linear velocities of the stone. Solution: In 10 s, the angle changes by 15 2 = 30 radians. So the angular speed of the stone is 45

Example 6 – Solution cont’d The distance traveled by the stone in 10 s is s = 15 2 r = 15 2 3 = 90 ft. So the linear speed of the stone is 46

Circular Motion 47

Example 7 – Finding Linear Speed from Angular Speed A woman is riding a bicycle whose wheels are 26 inches in diameter. If the wheels rotate at 125 revolutions per minute (rpm), find the speed at which she is traveling, in mi/h. Solution: The angular speed of the wheels is 2 125 = 250 rad/min. Since the wheels have radius 13 in. (half the diameter), the linear speed is v = r = 13 250 10, 210. 2 in. /min 48

Example 7 – Solution cont’d Since there are 12 inches per foot, 5280 feet per mile, and 60 minutes per hour, her speed in miles per hour is 9. 7 mi/h 49