Trigonometric Functions Contents 1 Radian Measure 2 AreaCircumference

Trigonometric Functions - Contents 1. Radian Measure 2. Area/Circumference/ Length of Arc 3. Area of a Sector 4. Area of a minor segment 5. Small Angles 6. 7. 8. 9. Trigonometric Results Trigonometric Graphs Graphical Solutions Derivatives of Trigonometric Functions 10. Integrals of Trigonometric Functions (Right Click Mouse Pointer Options Arrow Options Visible)

Radian Measure 1 t ni U 1 c 1 Unit One radian is the angle that a one unit arc makes with centre of a unit circle. Proof Circumference = 2πr = 2π (1) = 2π The circumference is 2π 2π = 360 o π = 180 o π radians = 180 o

Radian Measure Conversions Example 1 Convert 5π into degrees. 3 5π = 5 x 180 3 3 o = 300 o π = 180 Example 2 Convert 45 o into radians. 180 o = π radians 1 o = π/180 radians Example 3 Convert 1. 6 c into degrees. 45 o = π radians = 180 o 1 radians = 180/π deg 1. 6 radians = 180/ π x 1. 6 deg = 91 o 40’ π/ 180 x 45 radians = 45π/ 180 = π/ radians 4 radians

Area/Circumference/Length of Arc Circumference = 2 r = D Area = r 2 r Length of Arc l = r ( is in radians)

Area/Circumference/Length of Arc Circumference = 2 r = 2 D x 3 = 6 (exact) ≈ 18. 8 cm 4 Area = r 2 3 cm (Approximate) = x 32 = 9 (exact) Length of Arc ≈ 28. 3 cm 2 l = r (Approximate) ( is in radians) = 3 x /4 = 3 /4 (exact) ≈ 2. 4 cm (Approximate)

Area of a Sector Area of Sector A = ½ r 2 ( is in radians) r Proof Area of Sector = Angle Example Area of Circle Revolution A = Find the area of a sector with radius r 2 2 3 cm and angle /6. r 2 A = ½ r 2 = ½ 3 2 x /. 6 = 3 /4 cm 2. ≈ 2. 36 cm 2.

Area of a Minor Segment Area of Sector A = ½ r 2 ( - sin ) a b r ( is in radians) Find the area of a minor segment formed with radius 3 cm and angle /6. = ½ r 2 ( - sin ) Proof Area = ½ab sin Area of = Minor Sector Triangle Segment = ½ r 2 - ½ r 2 sin = ½ 32 x ( /6 - sin /6) = ½ 3 2 x ( / - ½ ) 6 = (3 /4 – 3/8)cm 2 ≈ 1. 98 cm 2. - Example = ½ r 2 ( - sin )

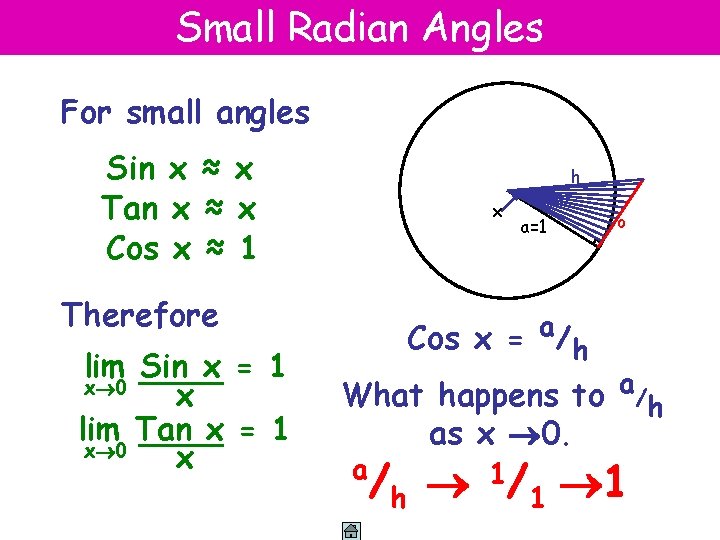
Small Radian Angles For small angles Sin x ≈ x Tan x ≈ x Cos x ≈ 1 Therefore lim Sin x = 1 x 0 x lim Tan x = 1 x 0 x h x a=1 o Cos x = a/h What happens to a/h as x 0. a /h 1/ 1 1

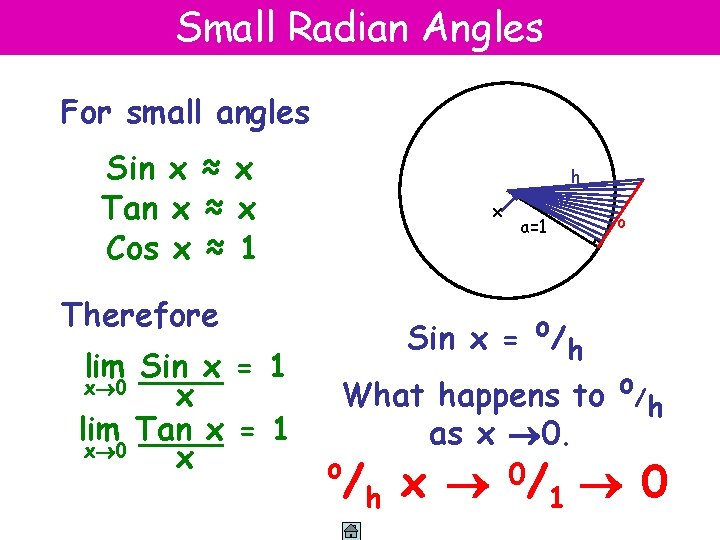
Small Radian Angles For small angles Sin x ≈ x Tan x ≈ x Cos x ≈ 1 Therefore lim Sin x = 1 x 0 x lim Tan x = 1 x 0 x h x o a=1 Sin x = o/h What happens to o/h as x 0. o /h x 0/ 1 0

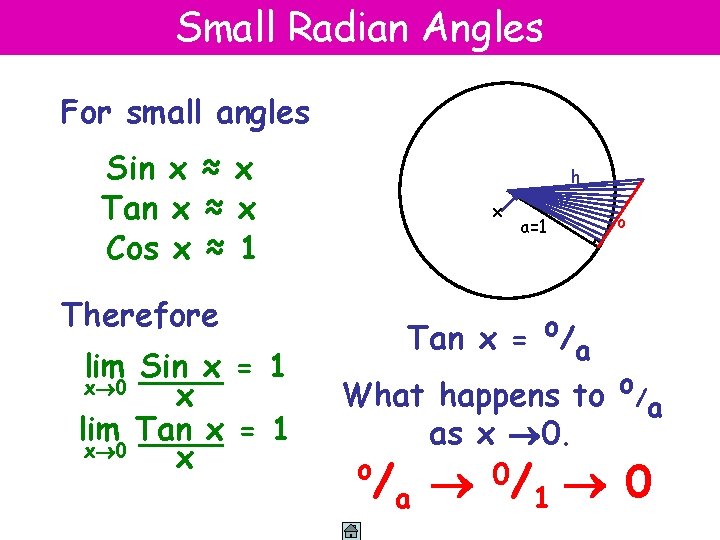
Small Radian Angles For small angles Sin x ≈ x Tan x ≈ x Cos x ≈ 1 Therefore lim Sin x = 1 x 0 x lim Tan x = 1 x 0 x h x a=1 o Tan x = o/a What happens to o/a as x 0. o /a 0/ 1 0

Small Radian Angles Example: Evaluate: lim Sin 5 x x 0 x lim Sin 5 x = lim 5(Sin 5 x) x 0 x 5 x (Sin 5 x) = 5 lim x 0 5 x = 5 x 1 = 5

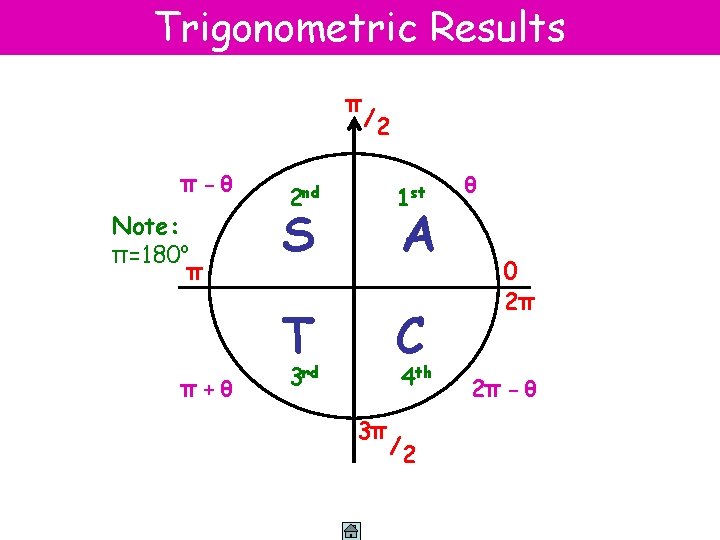
Trigonometric Results π π-θ Note: π=180 o π /2 2 nd 1 st S A T π+θ C 3 rd 4 th 3π /2 θ 0 2π 2π - θ

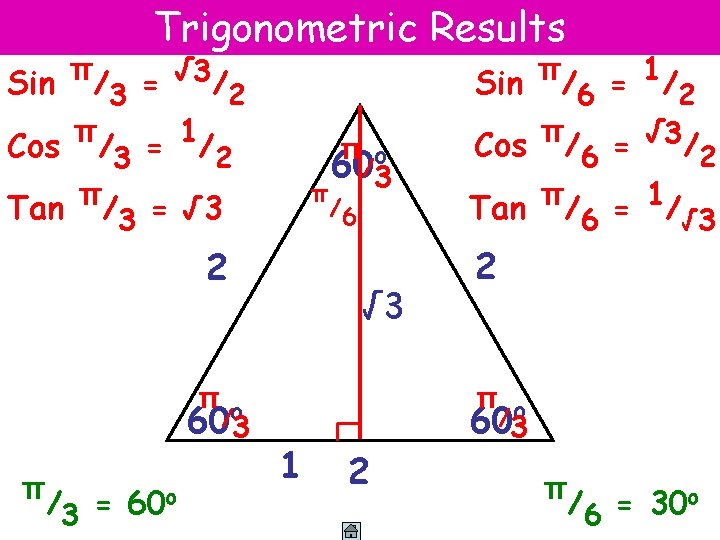
Trigonometric Results π √ Sin /3 = 3/2 π 1 Cos / = / 3 πo 60/3 π 2 Tan π/3 = √ 3 /6 2 πo 60/3 π/ = 60 o 3 √ 3 1 2 π 1 Sin /6 = /2 π √ 3 Cos / = / 6 2 Tan π/6 = 1/√ 3 2 π o 60/3 π/ = 30 o 6

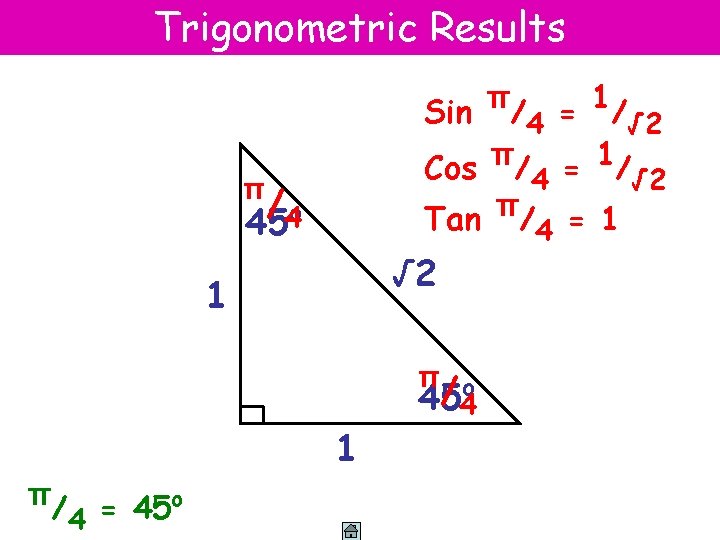
Trigonometric Results Sin π/4 = 1/√ 2 Cos π/4 = 1/√ 2 π Tan / = 1 π / 454 o √ 2 1 1 π/ = 45 o 4 π o /4 45 4

Trigonometric Results Find the exact value of: Sin 5π = Sin 5 x 180 4 4 = Sin 225 o o o = -Sin 45 = -1 √ 2 A T C Sin is -ve in the 3 rd Quadrant. o = Sin (180 + 45 ) o S

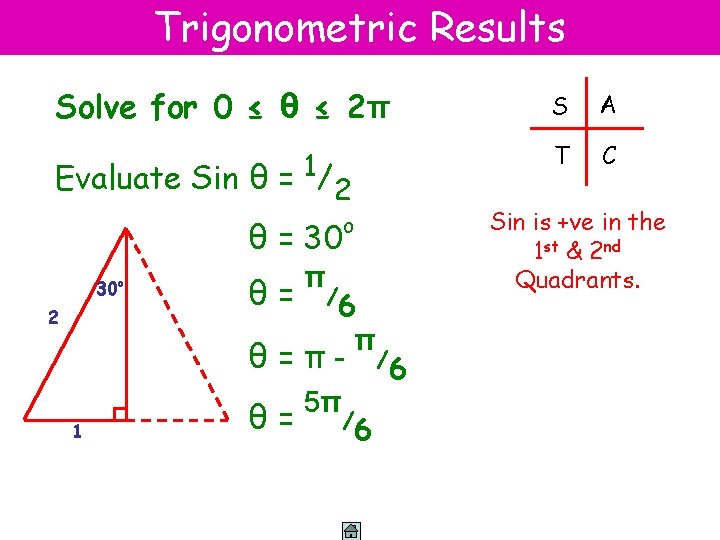
Trigonometric Results Solve for 0 ≤ θ ≤ 2π Evaluate Sin θ = 1/ 2 θ = 30 30 o 2 θ= π /6 θ=π1 θ= 5π /6 A T C Sin is +ve in the 1 st & 2 nd Quadrants. o π S /6

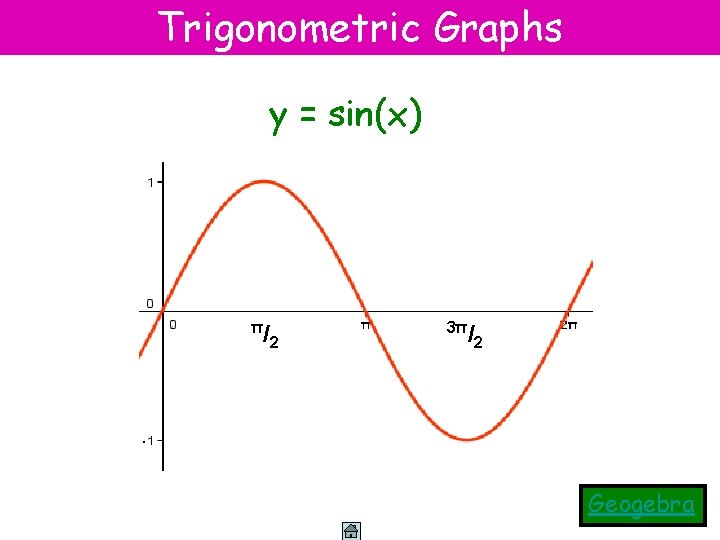
Trigonometric Graphs y = sin(x) π /2 3π /2 Geogebra

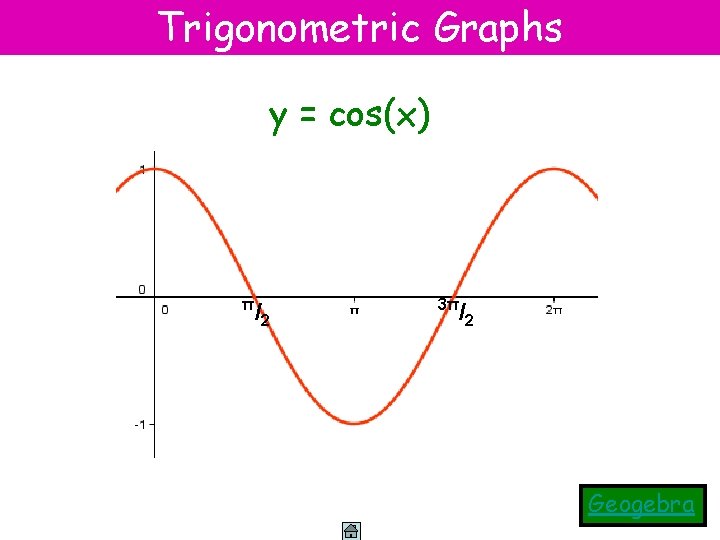
Trigonometric Graphs y = cos(x) π /2 3π /2 Geogebra

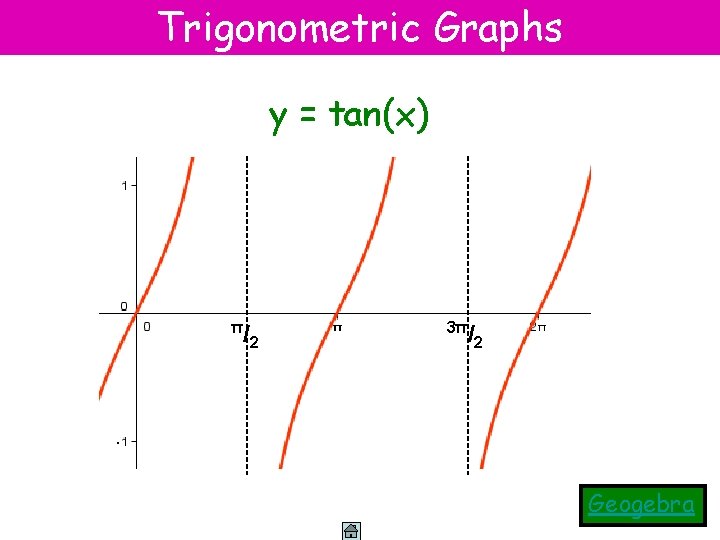
Trigonometric Graphs y = tan(x) π /2 3π /2 Geogebra

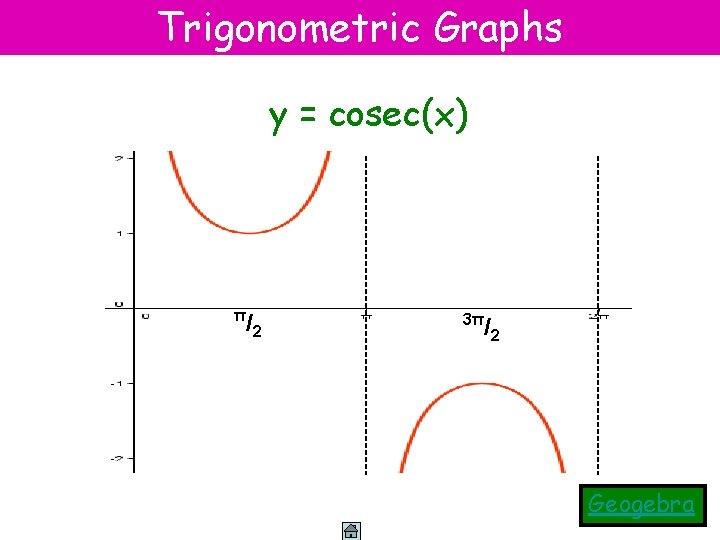
Trigonometric Graphs y = cosec(x) π /2 3π /2 Geogebra

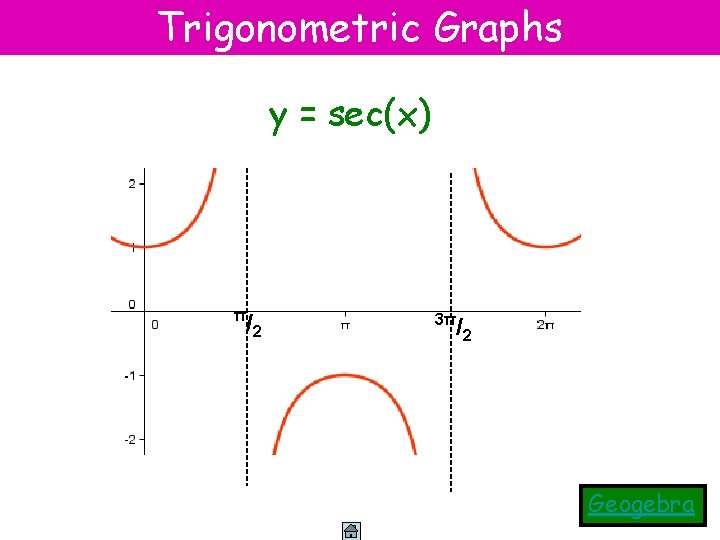
Trigonometric Graphs y = sec(x) π /2 3π /2 Geogebra

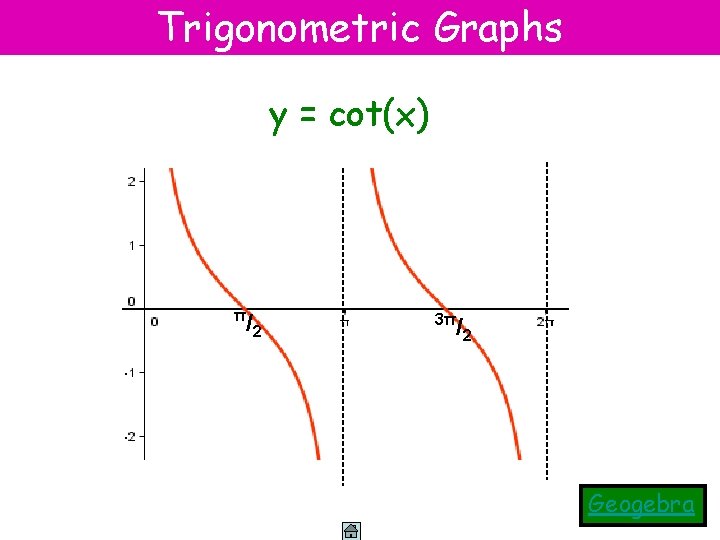
Trigonometric Graphs y = cot(x) π /2 3π /2 Geogebra

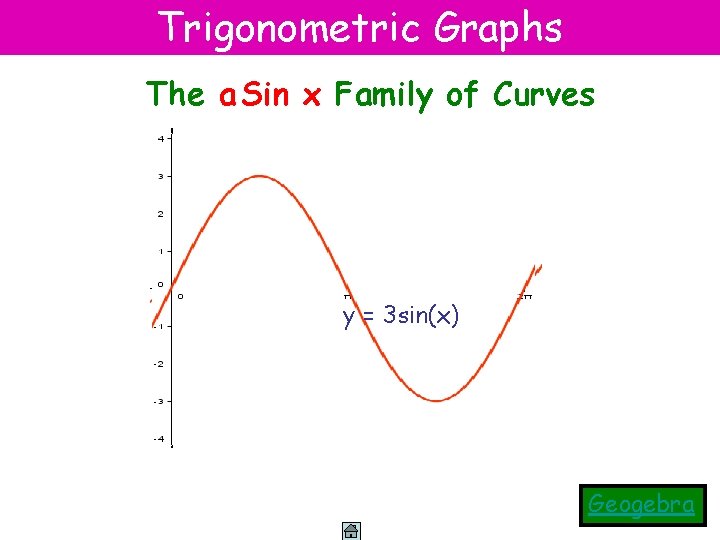
Trigonometric Graphs The a Sin x Family of Curves 3 sin(x) y =yy 4==sin(x) 2 sin(x) y = sin(x) Geogebra

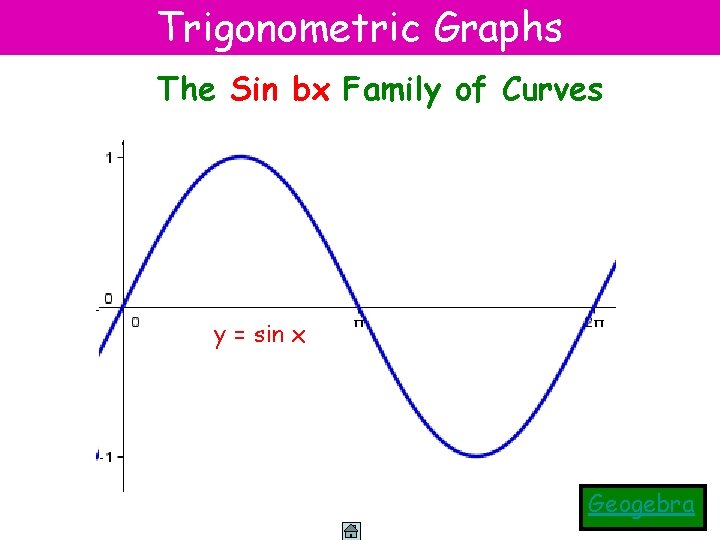
Trigonometric Graphs The Sin bx Family of Curves yy ==ysin 2 x sin = sin 3 x 4 x x Geogebra

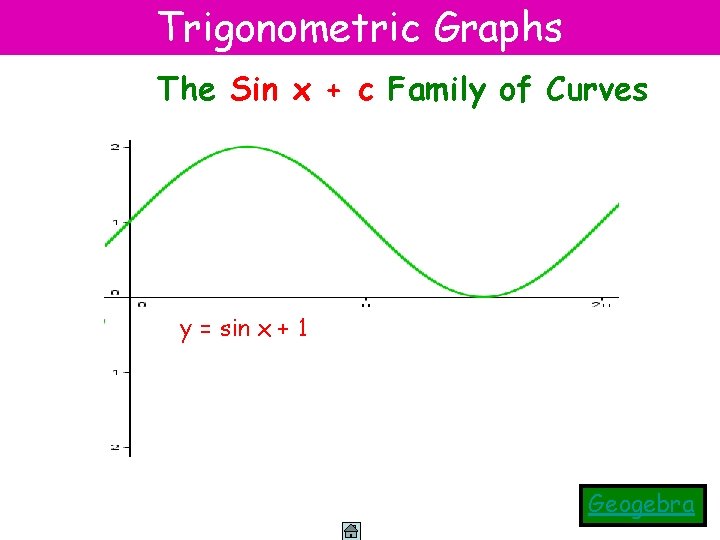
Trigonometric Graphs The Sin x + c Family of Curves y y= =sin sinx x+ 1 y = sin x - 1 Geogebra

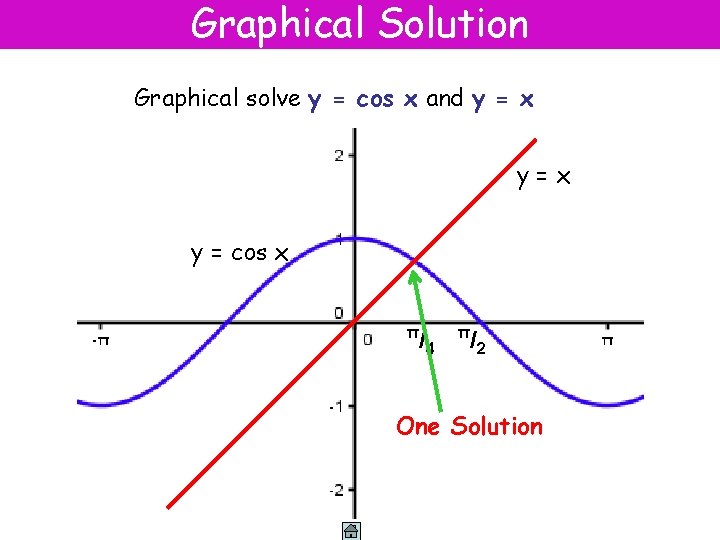
Graphical Solution Graphical solve y = cos x and y = x y=x y = cos x π /4 π /2 One Solution

Derivative of Trigonometric Functions Derivative Sin x Function of Function Rule d (sin x) = cos x dx d dx [sin f(x)] = f’(x) cos f(x) d (cos x) = sin x dx d [cos f(x)] = -f’(x) sin f(x) dx Cos x Tan x d (tan x) = sec 2 x dx d [tan f(x)] = f’(x) sec 2 f(x) dx

Derivative of Trigonometric Functions Derivative Examples Sin 4 x d (sin 4 x) = 4 cos 4 x dx d f(x)](3 x = f’(x) Tan + cos 1) f(x) dx [sin d [tan (3 x + 1)] = 3 sec 2 (3 x + 1) dx d [tan f(x)]2 = f’(x) sec 2 f(x) dx. Cos (x - 2 x + 1) d [cos (x 2 - 2 x + 1)] = -(2 x - 2) sin (x 2 -2 x + 1) dx 2 -2 x + 1) = 2(1 x) sin (x d [cos f(x)] = -f’(x) sin f(x) dx

Integrals of Trigonometric Functions Sin x Function of Function Rule Integral ∫sin x dx = - cos x + C 1 sin (ax +b) dx = /a cos (ax + b) + C ∫ Cos x ∫cos x dx = sin x + C cos (ax +b) dx = 1/ sin (ax + b) + C ∫ a Tan x ∫sec x dx = tan x + c 1 ∫sec (ax +b) dx = /a tan (ax + b) + C 2 2

Integral of Trigonometric Functions Integration Examples ∫ sin (ax +b) dx = - 1 /a cos (ax + b) + C ∫sin (3 x +2) dx = - /3 cos (3 x + 2) + C 1

Integral of Trigonometric Functions Integration Examples ∫sin x dx = - cos x + C π ∫sin x dx = 0 2 π - cos x 2 0 = - cosπ 2 - (-cos 0) = 0 – (-1) =1