Trigonometric Functions Angles and Their Measure 1 Measuring

Trigonometric Functions Angles and Their Measure 1

Measuring Angles l Two usual ways of measuring l Degrees l 360± l in one rotation Radians l 2¼ radians in one rotation 2

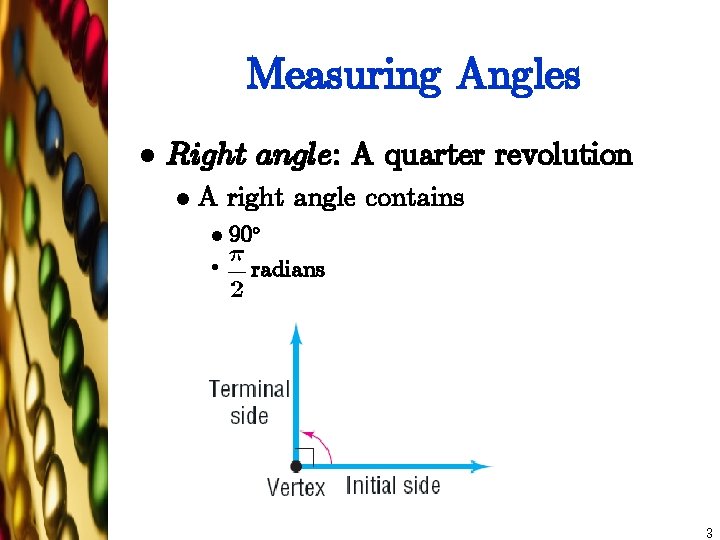
Measuring Angles l Right angle: A quarter revolution l A right angle contains l 90± l radians 3

Measuring Angles l Straight angle: A half revolution. l A straight angle contains: l 180± l¼ radians 4

Degrees, Minutes and Seconds l l One complete revolution = 360± One minute: One-sixtieth of a degree l One minute is denoted 10 l 1± = 600 l l One second: One-sixtieth of a minute l One second is denoted 100 l 10 = 6000 l 5

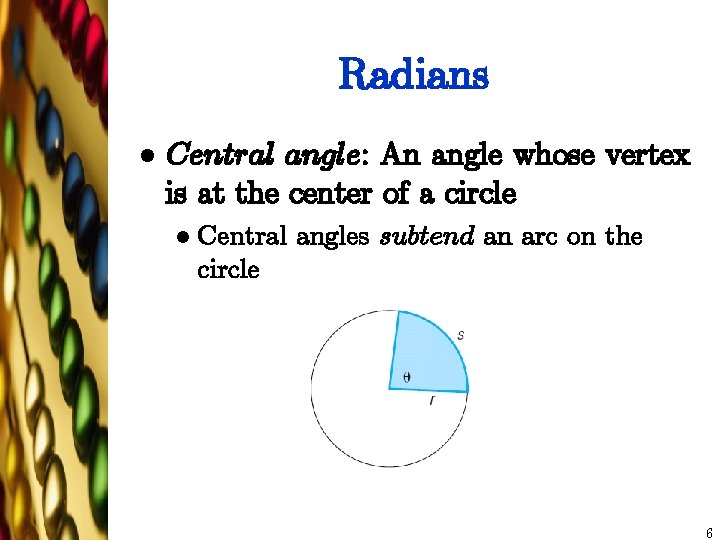
Radians l Central angle: An angle whose vertex is at the center of a circle l Central angles subtend an arc on the circle 6

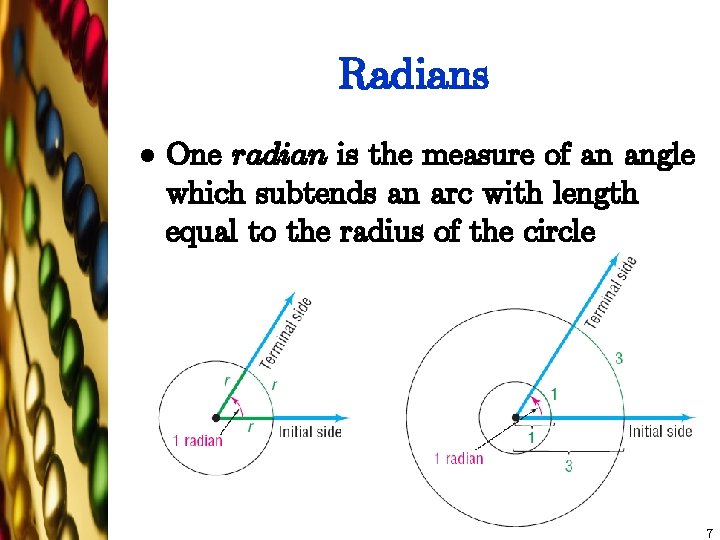
Radians l One radian is the measure of an angle which subtends an arc with length equal to the radius of the circle 7

Radians IMPORTANT! Radians are dimensionless l If an angle appears with no units, it must be assumed to be in radians l 8

Radians vs. Degrees l 9

Radians vs. Degrees l Measurements of common angles 10

Trigonometric Functions 11

Circles of Radius r l Theorem. For an angle µ in standard position, let P = (x, y) be the point on the terminal side of µ that is also on the circle x 2 + y 2 = r 2. Then 12

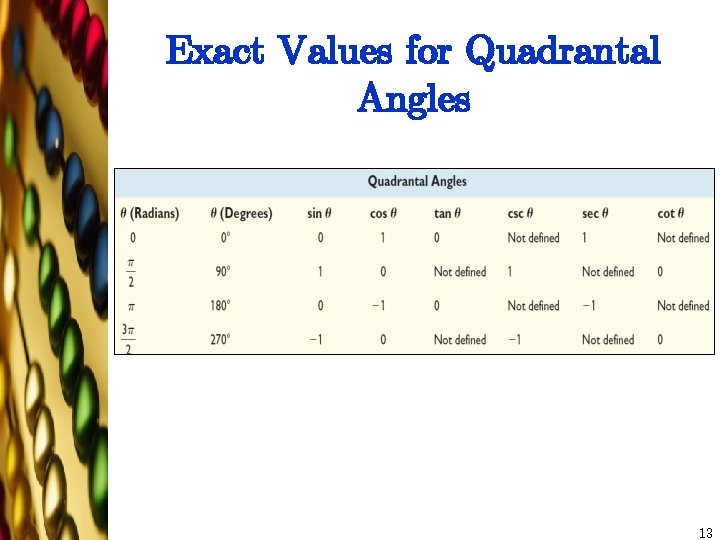
Exact Values for Quadrantal Angles 13

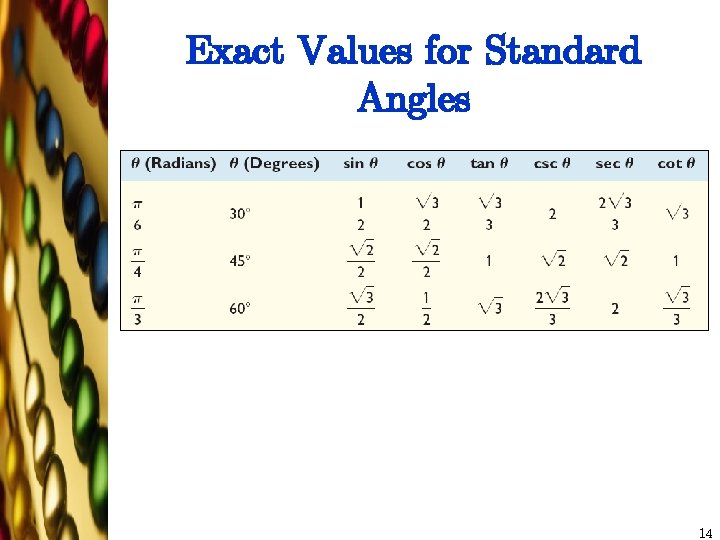
Exact Values for Standard Angles 14

Properties of the Trigonometric Functions 15

Domains of Trigonometric Functions l l l Domain of sine and cosine functions is the set of all real numbers Domain of tangent and secant functions is the set of all real numbers, except odd integer multiples of = 90± Domain of cotangent and cosecant functions is the set of all real numbers, except integer multiples of ¼ = 180± 16

Ranges of Trigonometric Functions l Sine and cosine have range [{1, 1] {1 · sin µ · 1; jsin µj · 1 l {1 · cos µ · 1; jcos µj · 1 l l Range of cosecant and secant is ({1, {1] [ [1, 1) jcsc µj ¸ 1 l jsec µj ¸ 1 l l Range of tangent and cotangent functions is the set of all real numbers 17

Periods of Trigonometric Functions l Periodic Properties: sin(µ + 2¼) = sin µ cos(µ + 2¼) = cos µ tan(µ + ¼) = tan µ csc(µ + 2¼) = csc µ sec(µ + 2¼) = sec µ cot(µ + ¼) = cot µ l l Sine, cosecant and secant have period 2¼ Tangent and cotangent have period ¼ 18

Signs of the Trigonometric Functions l P = (x, y) corresponding to angle µ l l Definitions of functions, where defined Find the signs of the functions Quadrant l I: x > 0, y > 0 II: x < 0, y > 0 III: x < 0, y < 0 IV: x > 0, y < 0 19

Signs of the Trigonometric Functions 20

Pythagorean Identities l l Unit circle: x 2 + y 2 = 1 (sin µ)2 + (cos µ)2 = 1 sin 2 µ + cos 2 µ = 1 tan 2 µ + 1 = sec 2 µ 1 + cot 2 µ = csc 2 µ 21

Even-Odd Properties l l A function f is even if f({µ) = f(µ) for all µ in the domain of f A function f is odd if f({µ) = {f(µ) for all µ in the domain of f 22

Even-Odd Properties l Theorem. [Even-Odd Properties] sin({µ) = {sin(µ) cos({µ) = cos(µ) tan({µ) = {tan(µ) csc({µ) = {csc(µ) sec({µ) = sec(µ) cot({µ) = {cot(µ) l l Cosine and secant are even functions The other functions are odd functions 23

Fundamental Trigonometric Identities l Quotient Identities l Reciprocal Identities l Pythagorean Identities l Even-Odd Identities 24