Trigonometric Function Graphs General Right Triangle B c

Trigonometric Function Graphs

General Right Triangle B c A a b C General Trigonometric Ratios SOH CAH TOA

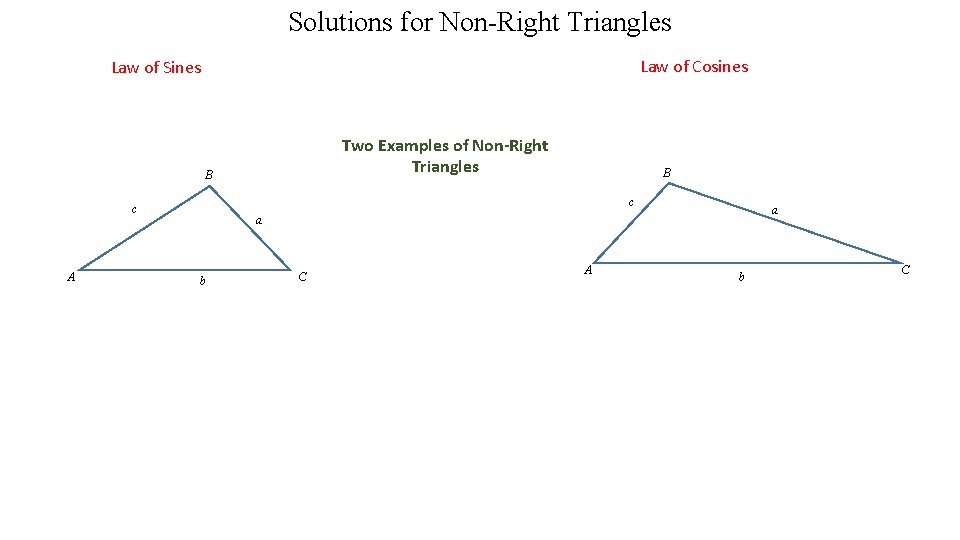
Solutions for Non-Right Triangles Law of Cosines Law of Sines Two Examples of Non-Right Triangles B c c A B a a b C A b C

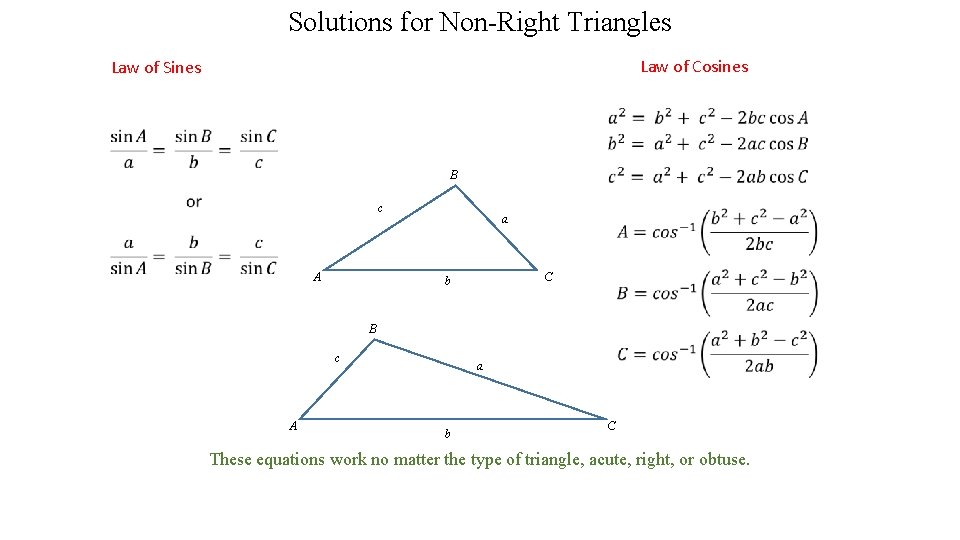
Solutions for Non-Right Triangles Law of Cosines Law of Sines B c A a C b B c A a b C These equations work no matter the type of triangle, acute, right, or obtuse.

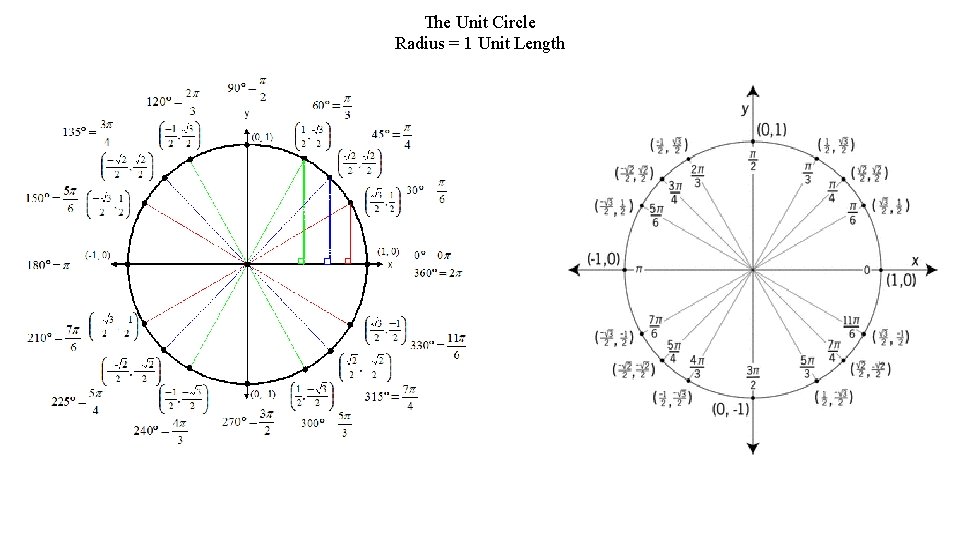
The Unit Circle Radius = 1 Unit Length

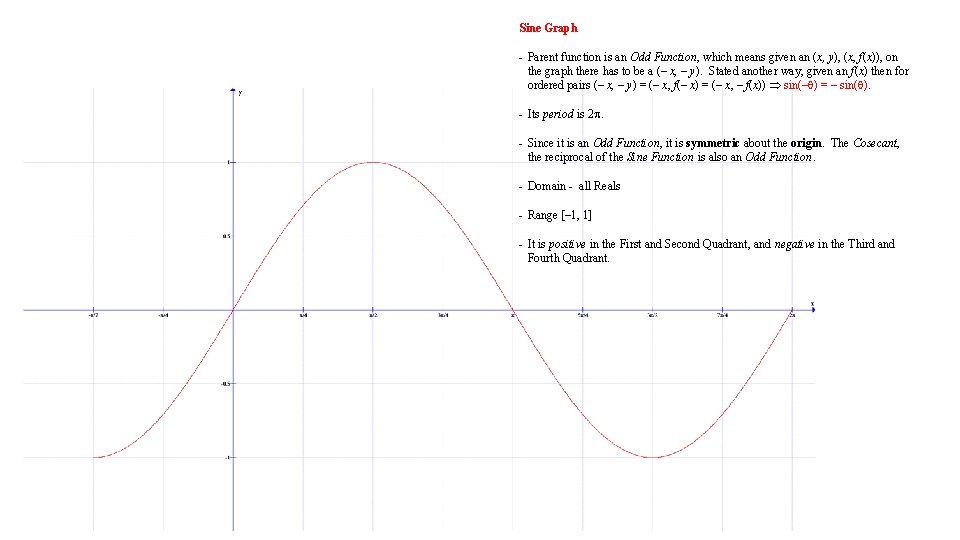
Sine Graph - Parent function is an Odd Function, which means given an (x, y), (x, f(x)), on the graph there has to be a (– x, – y). Stated another way, given an f(x) then for ordered pairs (– x, – y) = (– x, f(– x) = (– x, – f(x)) sin(– ) = – sin( ). - Its period is 2. - Since it is an Odd Function, it is symmetric about the origin. The Cosecant, the reciprocal of the Sine Function is also an Odd Function. - Domain - all Reals - Range [– 1, 1] - It is positive in the First and Second Quadrant, and negative in the Third and Fourth Quadrant.

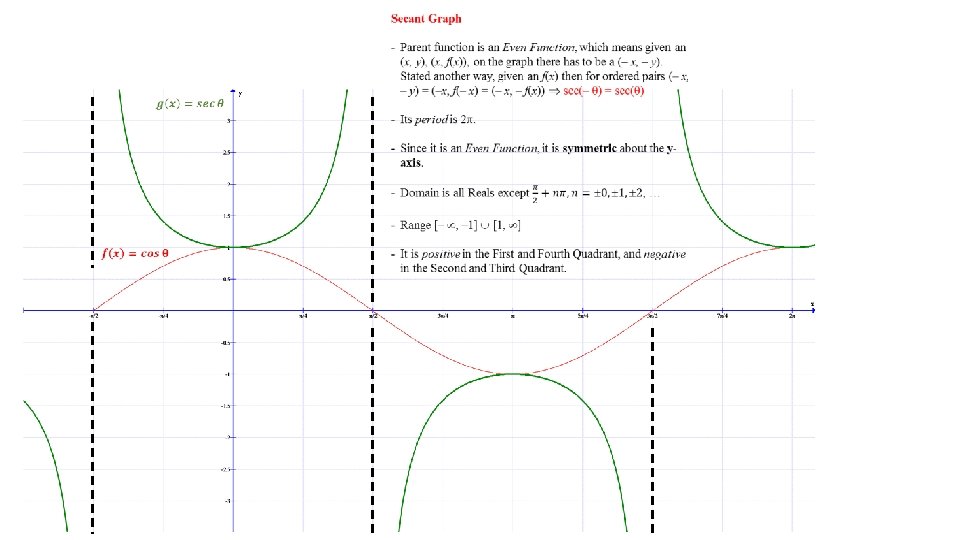
Cosine Graph - Parent function is an Even Function, which means given an (x, y), (x, f(x)), on the graph there has to be a (– x, y). Stated another way, given an f(x) then for ordered pairs (– x, y) = (– x, f(– x) = (– x, f(x)) cos(– ) = cos( ) - Its period is 2. - Since it is an Even Function, it is symmetric about the y-axis. The Secant, the reciprocal of the Cosine Function, is also an Even Function. - Domain - all Reals - Range [– 1, 1] - It is positive in the First and Fourth Quadrant, and negative in the Second and Third Quadrant

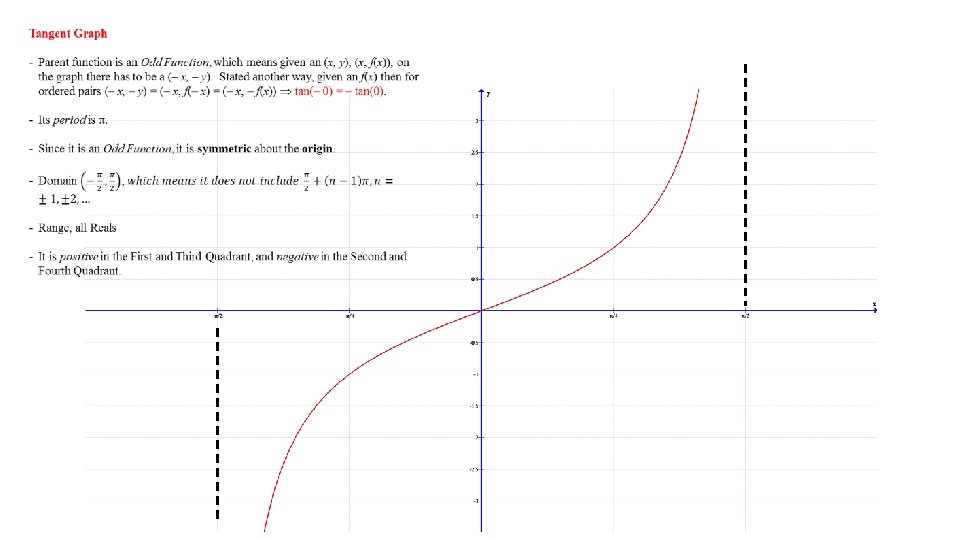
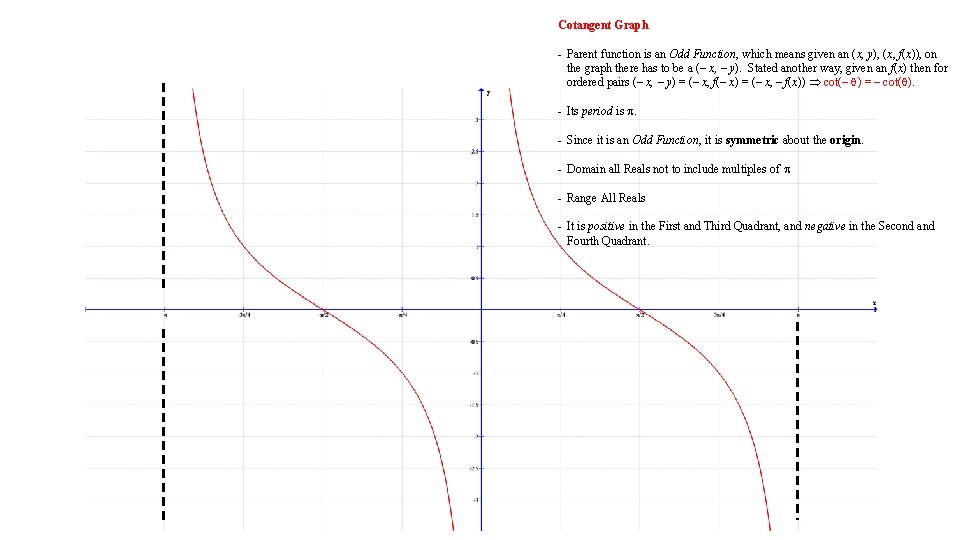
Cotangent Graph - Parent function is an Odd Function, which means given an (x, y), (x, f(x)), on the graph there has to be a (– x, – y). Stated another way, given an f(x) then for ordered pairs (– x, – y) = (– x, f(– x) = (– x, – f(x)) cot(– ) = – cot( ). - Its period is . - Since it is an Odd Function, it is symmetric about the origin. - Domain all Reals not to include multiples of - Range All Reals - It is positive in the First and Third Quadrant, and negative in the Second and Fourth Quadrant.

Arc Functions

Arccosine, cos– 1, Function - It is the inverse function of the cosine, which means cos– 1(cos ) = and cos(cos– 1 ½) = ½. - Domain [– 1, 1] - Range [0, ] - The value of the arccosine is an angle.

END OF LINE