Trigonometric Equations with Multiple Angles The diagram shows

Trigonometric Equations with Multiple Angles

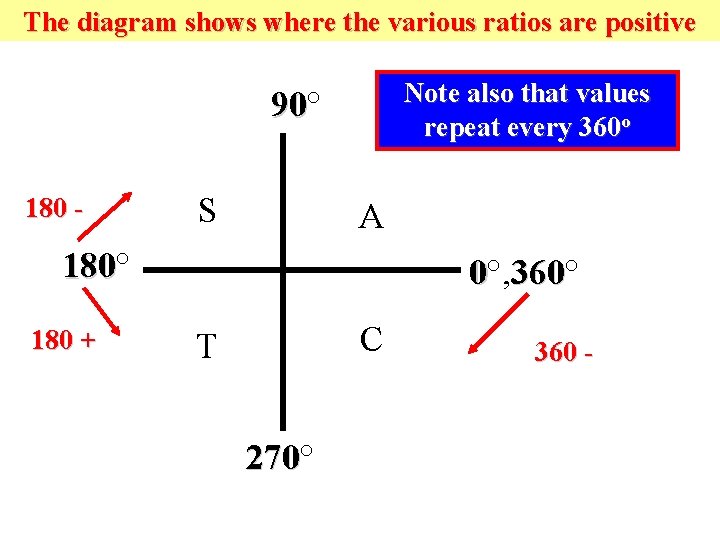
The diagram shows where the various ratios are positive Note also that values repeat every 360 o 90° 90 180 - S A 180° 180 + 0°, 360° 360 C T 270° 270 360 -

Solve cos 3 x = – 1/√ 2 for values of x such that 0 < x < π First of all consider the range of values If 0 < x < π then 0 < 3 x < 3π (540 o) o = to o Work in Remember degrees then 3π change = 3 × 180 back 540 radians later Now find BASE angle cos -1 (1/√ 2 ) = 45 o π/ 4 S 180 – A Since cosine negative T C o o o 3 x = 135 , 225 495 180 + Now change back to radians using multiples of π/4 3 x = 3π/4 , 5π/4 , 11π/4 So x = 3π/12 , 5π/12 , 11π/12

Solve sin 2 x = 1/2 for values of x such that 0 < x < 2π First of all consider the range of values If 0 < x < 2π then 0 < 2 x < 4π (720 o) o = to o Work in Remember degrees. Now then find change back angle radians later 4π = 4 BASE × 180 720 sin -1 (1/2 ) = 30 o π/ 6 S 180 – A Since sine positive T C o o 2 x = 30 , 150 390 , 510 Now change back to radians using multiples of π/6 2 x = π/6 , 5π/6 , 13π/6 , 17π/6 So x = π/12 , 5π/12 , 13π/12 , 17π/12

Solve tan 4 x = √ 3 for values of x such that 0 < x < π First of all consider the range of values If 0 < x < π then 0 < 4 x < 4π (720 o) o =to o Work in degrees Remember Now then find 4πchange =BASE 4 × 180 back angle 720 radians later tan -1 (√ 3 ) = 60 o π/ 3 S A Since tangent positive T C 180 + o o 4 x = 60 , 240 420 , 600 Now change back to radians using multiples of π/3 4 x = π/3 , 4π/3 , 7π/3 , 10π/3 So x = π/12 , π/3 , 7π/12 , 5π/6

Solve 2 sin (2 x – π/6) = √ 3 for values of x such that 0 < x < 2π First of all consider the range of values If 0 < x < 2π then 0 < 2 x – π/6 < 4π – π/6) (690 o) π/ change o – to o = 690 olater Work Remember in degrees Now 2πthen –find = BASE 2 × 180 back angle 30 radians 6 sin -1 (√ 3/2 ) = 60 o 2 x – π/ 6 = 60 o , π/ 120 o 180 - 3 420 o , 480 o S A T C Now change back to radians using multiples of π/3 2 x – π/6 = π/3 , 2π/3 , 7π/3 , 8π/3 2 x = 3π/ 6 , 5π/ 6 , 15π/ 6 , 17π/ 6 So x = π/4 , 5π/12 , 5π/6 , 17π/12