Trigonometria no Tringulo Retngulo Relacionando lados e ngulos

Trigonometria no Triângulo Retângulo

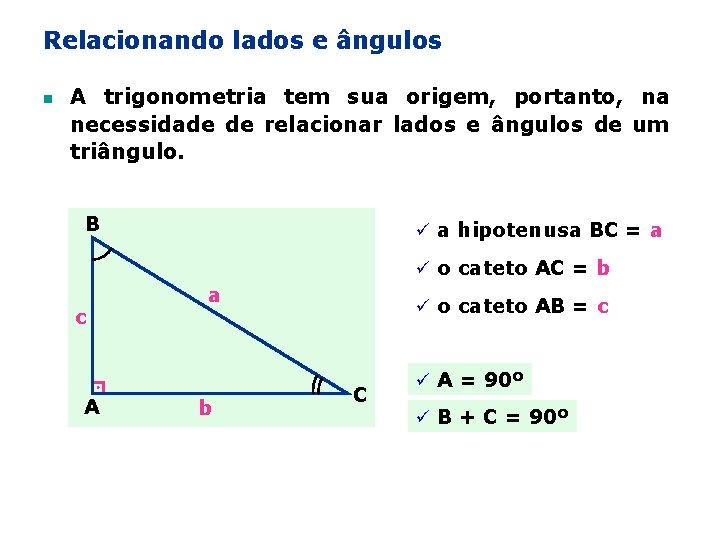
Relacionando lados e ângulos n A trigonometria tem sua origem, portanto, na necessidade de relacionar lados e ângulos de um triângulo. B ü a hipotenusa BC = a ü o cateto AC = b c A a b ü o cateto AB = c C ü A = 90º ü B + C = 90º

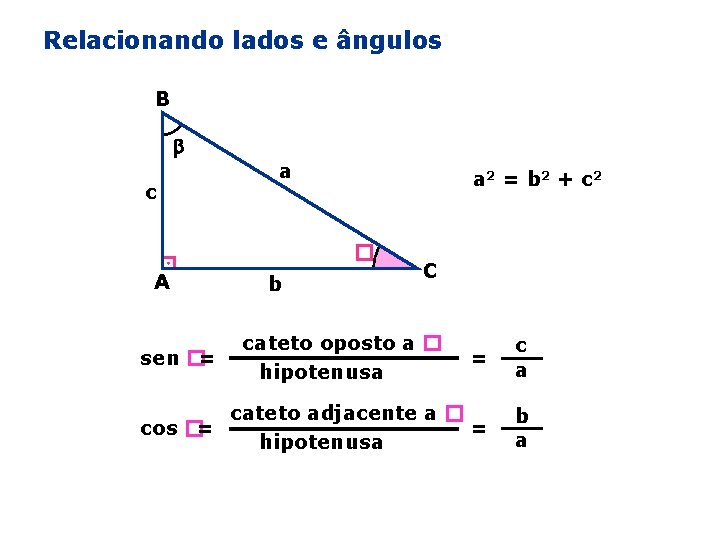
Relacionando lados e ângulos B c a a 2 = b 2 + c 2 � A sen �= cos �= b C cateto oposto a � hipotenusa = c a cateto adjacente a � = hipotenusa b a

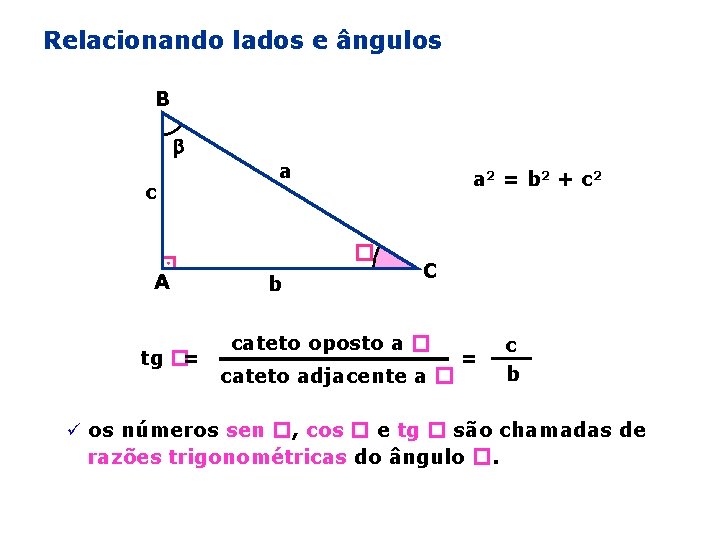
Relacionando lados e ângulos B c a a 2 = b 2 + c 2 � A tg �= b C cateto oposto a � cateto adjacente a � = c b ü os números sen �, cos � e tg � são chamadas de razões trigonométricas do ângulo �.

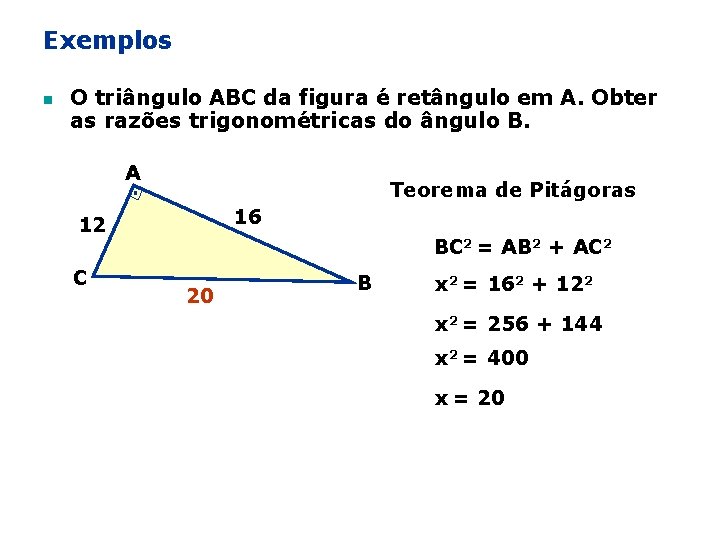
Exemplos n O triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas do ângulo B. A Teorema de Pitágoras 16 12 C BC 2 = AB 2 + AC 2 20 B x 2 = 162 + 122 x 2 = 256 + 144 x 2 = 400 x = 20

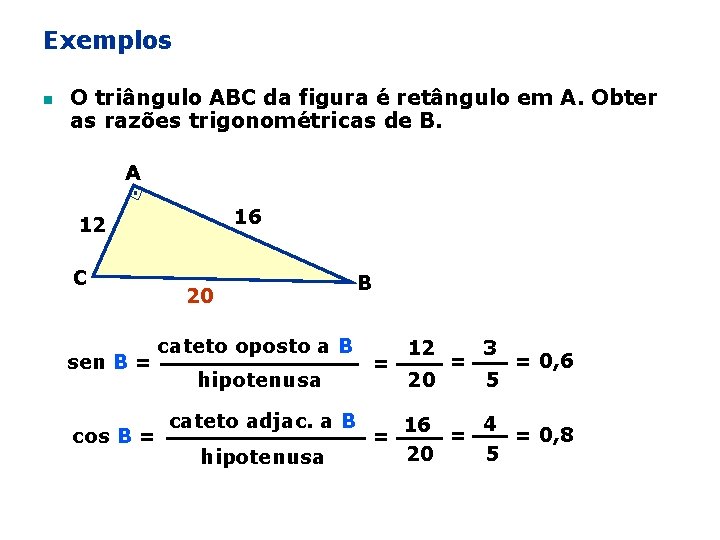
Exemplos n O triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas de B. A 16 12 C sen B = cos B = 20 cateto oposto a B hipotenusa cateto adjac. a B hipotenusa B = = 12 20 = 3 5 = 0, 6 4 16 = = 0, 8 20 5

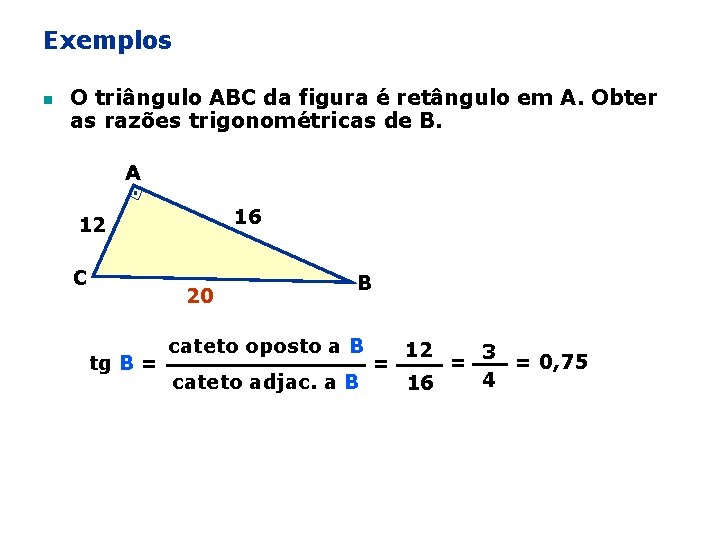
Exemplos n O triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas de B. A 16 12 C 20 tg B = B cateto oposto a B cateto adjac. a B = 12 16 = 3 = 0, 75 4

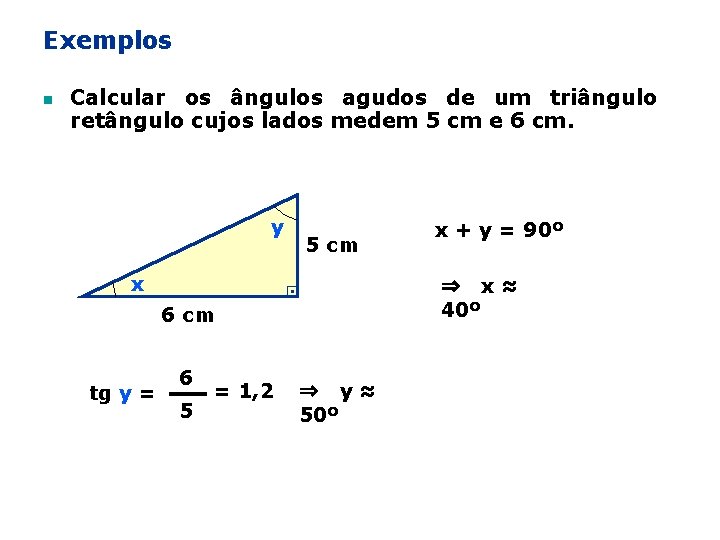
Exemplos n Calcular os ângulos agudos de um triângulo retângulo cujos lados medem 5 cm e 6 cm. 16 y 5 cm x ⇒ x≈ 40º 6 cm tg y = 6 5 = 1, 2 x + y = 90º ⇒ y≈ 50º

Outras razões trigonométricas

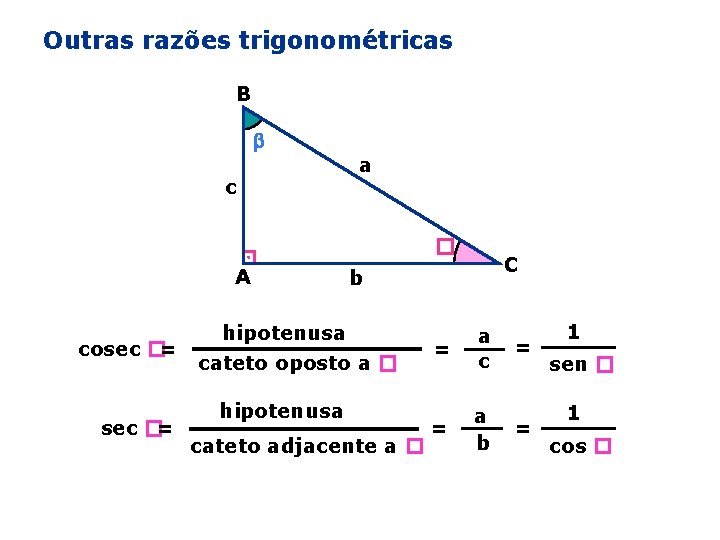
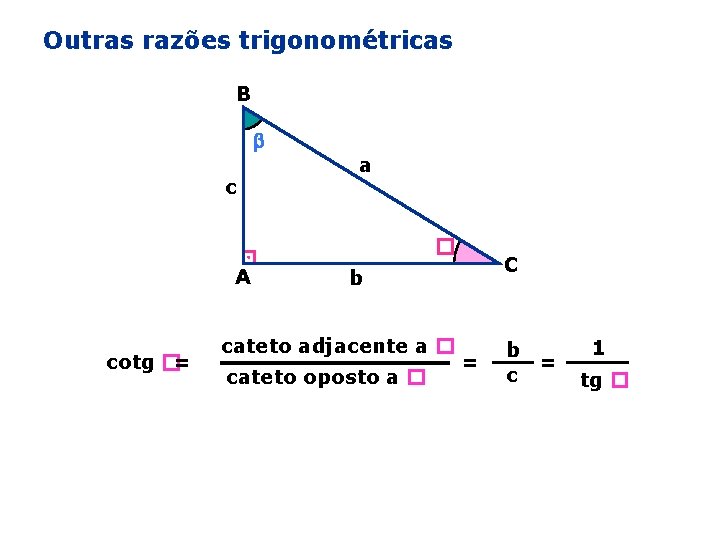
Outras razões trigonométricas B c a � A cosec �= C b hipotenusa cateto oposto a � hipotenusa cateto adjacente a � = a c = = a b = 1 sen � 1 cos �

Outras razões trigonométricas B c a � A cotg �= C b cateto adjacente a � cateto oposto a � = b = c 1 tg �

Seno, co-seno e tangente de ângulos complementares

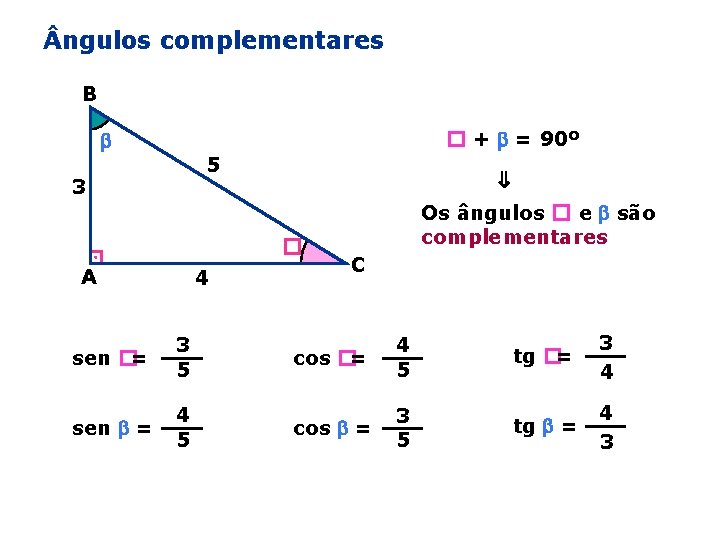
ngulos complementares B � + = 90º 3 ⇒ 5 � A 4 sen �= 3 5 sen = 4 5 Os ângulos � e são complementares C cos �= 4 5 tg �= 3 4 cos = 3 5 tg = 4 3

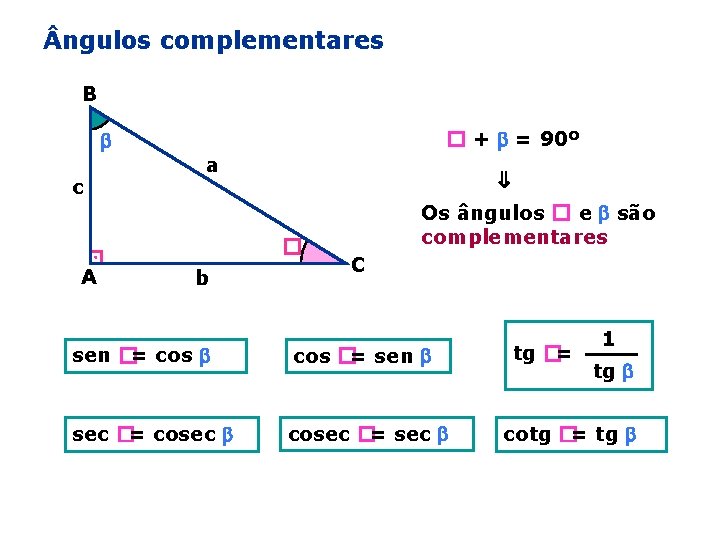
ngulos complementares B a ⇒ c � + = 90º � A b Os ângulos � e são complementares C sen �= cos �= sen sec �= cosec �= sec tg �= 1 tg cotg �= tg

Exemplo n No triângulo retângulo da figura, temos: I. sen t = ½ II. sec t = III. tg t = 2 √ 5 2 1 cm t 2 cm A(s) afirmativa(s) verdadeira(s) é(são): a) I b) II c) III d) II e III e) I, II e III

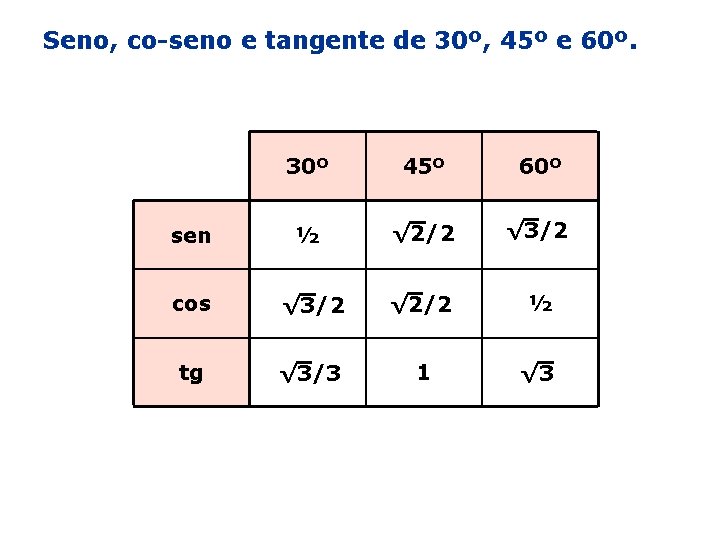
Seno, co-seno e tangente de 30º, 45º e 60º.

Seno, co-seno e tangente de 30º, 45º e 60º. 30º 45º 60º sen ½ √ 2/2 √ 3/2 cos √ 3/2 √ 2/2 ½ tg √ 3/3 1 √ 3

Exemplos n A partir dos dados apresentados na figura, determinar as medidas indicadas por x e y. cm 16 2 1 x 30º y sen 30º = cos 30º = x 12 y 12 ⇒ x = 12. 1/2 ⇒ x = 12. √ 3/2 ⇒ ⇒ x = 6 cm x = 6 √ 3 cm

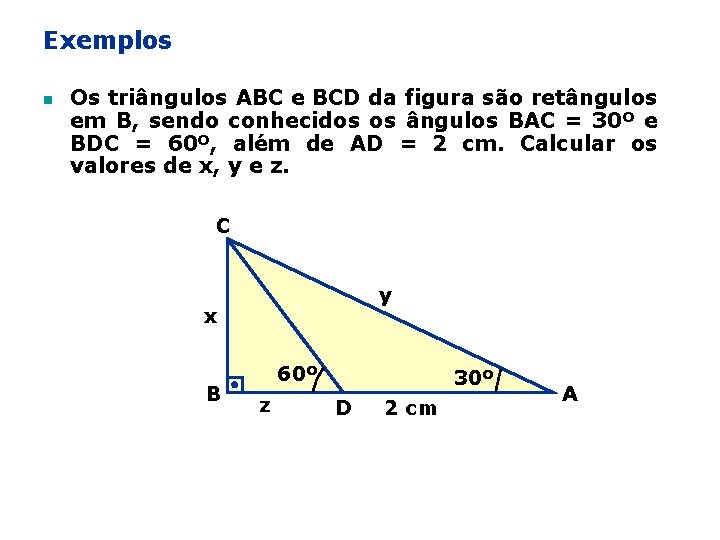
Exemplos n Os triângulos ABC e BCD da figura são retângulos em B, sendo conhecidos os ângulos BAC = 30º e BDC = 60º, além de AD = 2 cm. Calcular os valores de x, y e z. C y x B 60º z 30º D 2 cm A

Identidades trigonométricas

Identidades trigonométricas n Ferramentas de utilizadas para: grande aplicabilidade sendo ü Obter uma razão trigonométrica, para um dado ângulo, a partir de outra razão cujo valor seja conhecido. ü Simplificar expressões extensas envolvendo várias relações trigonométricas para um mesmo ângulo.

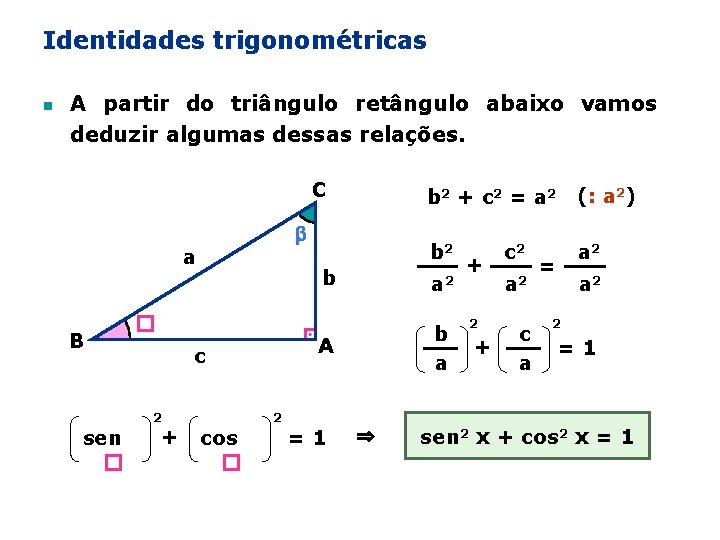
Identidades trigonométricas n A partir do triângulo retângulo abaixo vamos deduzir algumas dessas relações. C a � B c sen � 2 + cos � 2 b 2 + c 2 = a 2 (: a 2) b 2 a 2 b a 2 A b a =1 ⇒ + 2 + c 2 a 2 c a = a 2 2 =1 sen 2 x + cos 2 x = 1

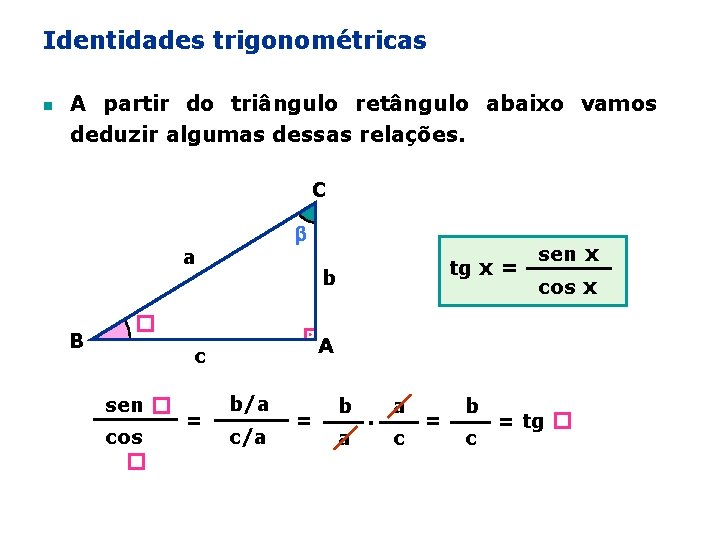
Identidades trigonométricas n A partir do triângulo retângulo abaixo vamos deduzir algumas dessas relações. C a B b � cos � = sen x cos x A c sen � tg x = b/a c/a = b a . a c = b c = tg �

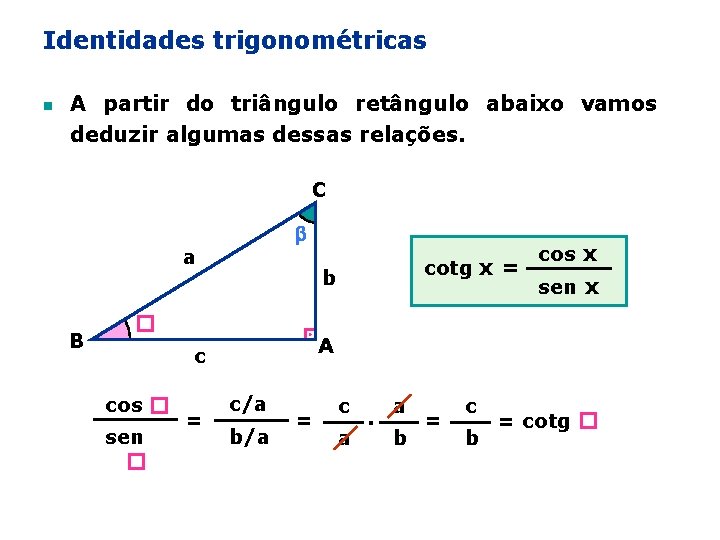
Identidades trigonométricas n A partir do triângulo retângulo abaixo vamos deduzir algumas dessas relações. C a B b � sen � = cos x sen x A c cos � cotg x = c/a b/a = c a . a b = cotg �

Identidades trigonométricas - Resumo 1) sen 2 x + cos 2 x = 1 2) tg x = sen x ü (cos x ≠ 0) cos x 3) cotg x = 4) sec x = ü Relação fundamental sen x 1 cos x 5) cosec x = = 1 tg x ü (sen x ≠ 0) ü (cos x ≠ 0) 1 sen x ü (sen x ≠ 0)

Exemplos n Demonstre que sec 2 x = 1 + tg 2 x. sec x = 1 cos x ⇒ sec 2 x = ⇒ 1 cos 2 x sen 2 x + cos 2 x sen 2 x cos 2 x + sec 2 x = tg 2 x + 1 cos 2 x

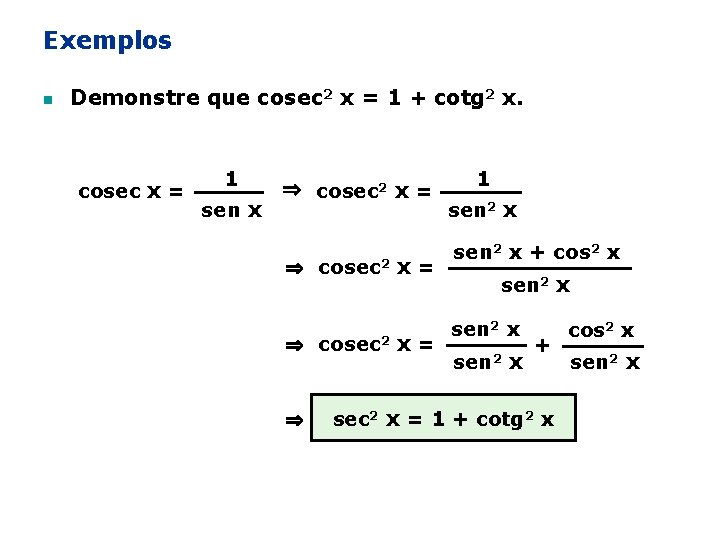
Exemplos n Demonstre que cosec 2 x = 1 + cotg 2 x. cosec x = 1 sen x ⇒ cosec 2 x = ⇒ 1 sen 2 x + cos 2 x sen 2 x + sec 2 x = 1 + cotg 2 x cos 2 x sen 2 x

Exemplos n Sabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno, tangente, cotangente, secante e a co-secante desse ângulo. sen 2 x + cos 2 x ⇒ ⇒ 3 5 9 25 2 + cos 2 x = 1 ⇒ cos 2 x = 1 – 25 – 9 9 = 25 25 = ⇒ cos x = ± 4/5 ⇒ cos x = 4/5 16 25

Exemplos n Sabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno, tangente, cotangente, secante e a co-secante desse ângulo. tg x = sen x cos x cotg x = 1 tg x = = 3 5 4 5 1 3 4 3 = 4 4 = 3

Exemplos n Sabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno, tangente, cotangente, secante e a co-secante desse ângulo. sec x = 1 cos x cosec x = 1 4 5 = 1 sen x = = 1 3 5 5 4 5 = 3

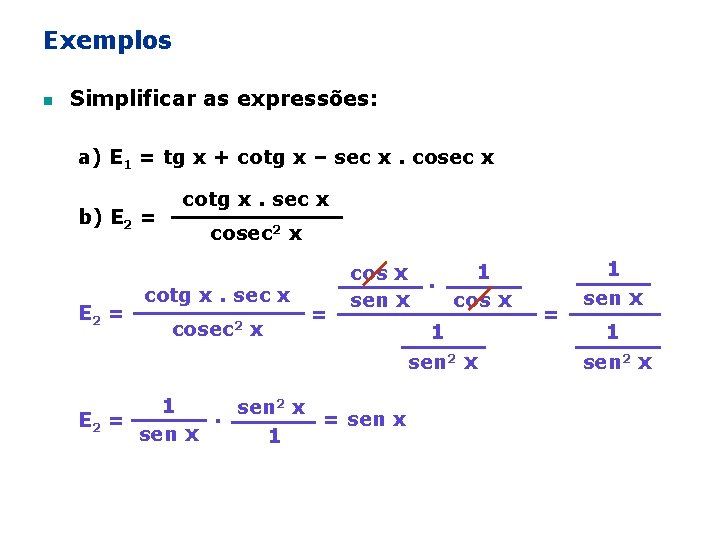
Exemplos n Simplificar as expressões: a) E 1 = tg x + cotg x – sec x. cosec x b) E 2 = cotg x. sec x cosec 2 x E 1 = tg x + cotg x – sec x. cosec x sen x E 1 = cos x + sen x 1 1. – cos x sen 2 x + cos 2 x – 1 E 1 = sen x. cos x = 1– 1 sen x. cos x =0

Exemplos n Simplificar as expressões: a) E 1 = tg x + cotg x – sec x. cosec x b) E 2 = cotg x. sec x cosec 2 x = 1 cos x. sen x cos x 2 x 1 sen. = sen x E 2 = sen x 1 1 sen 2 x = 1 sen x 1 sen 2 x

ngulos e arcos na circunferência

Circunferência A B P r r O r E r D C

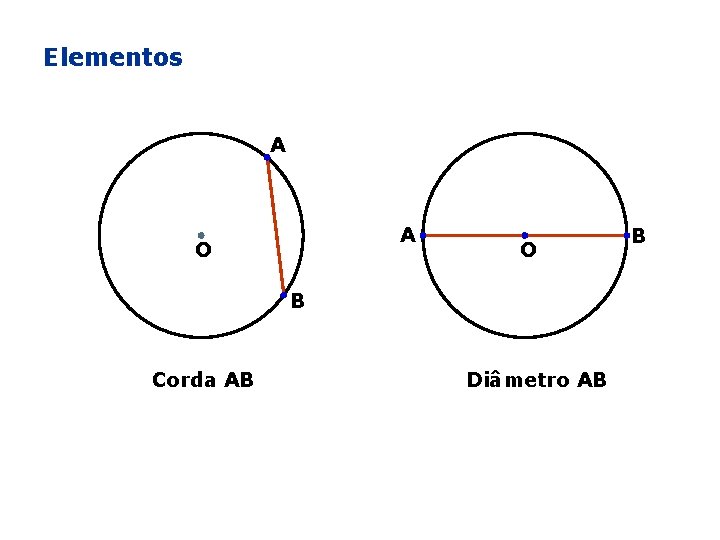
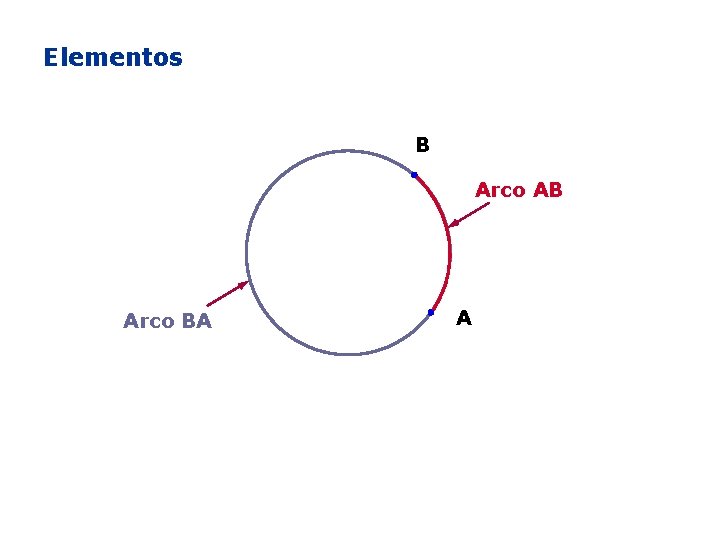
Elementos A A O O B Corda AB Diâmetro AB B

Elementos B Arco AB Arco BA A

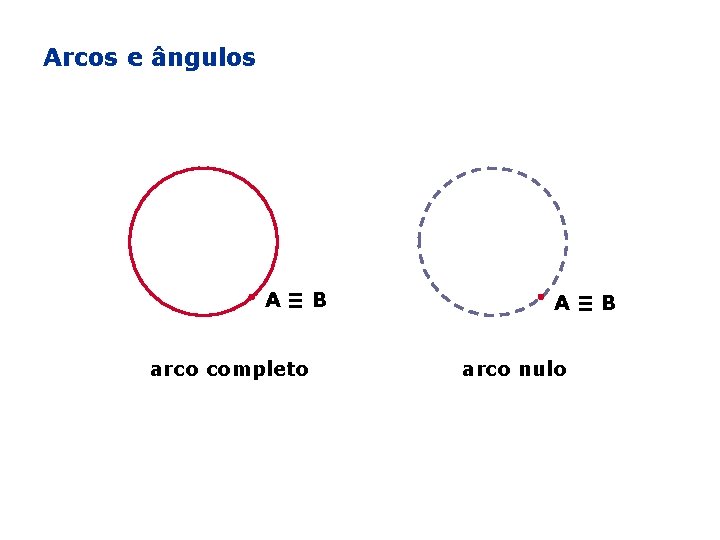
Arcos e ângulos A≡B arco completo A≡B arco nulo

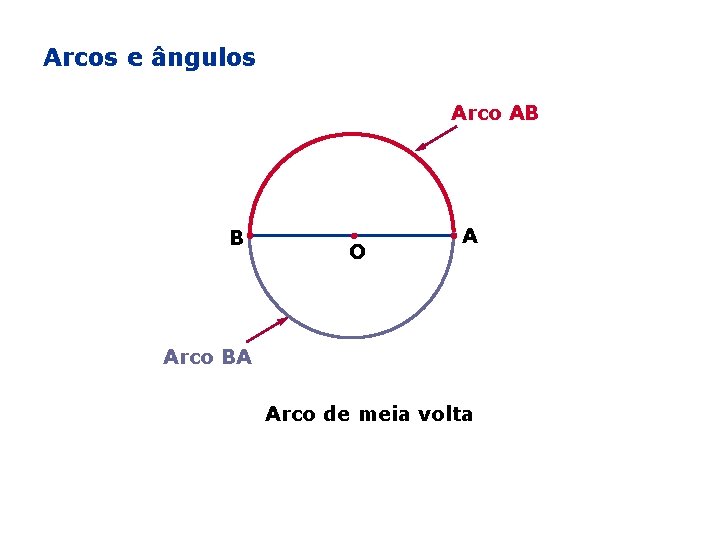
Arcos e ângulos Arco AB B O A Arco BA Arco de meia volta

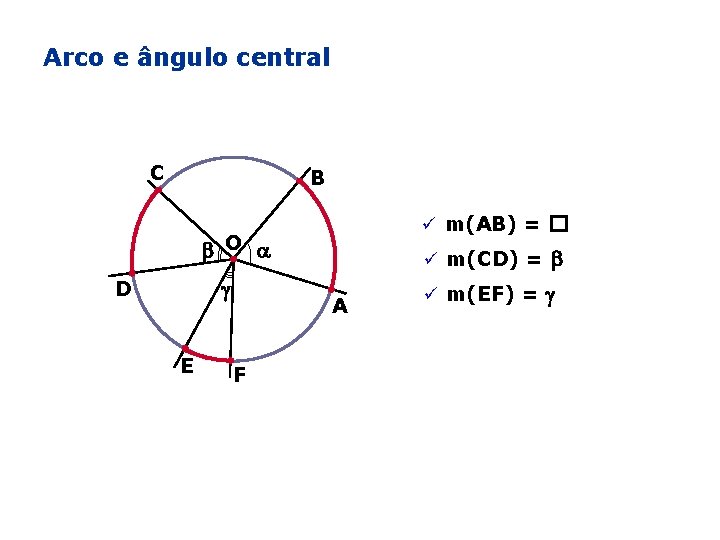
Arco e ângulo central C B ü m(AB) = � O D E ü m(CD) = A F ü m(EF) =

O grau como unidade de medida 120 o 110 o 100 o 90 o 80 o 70 o 60 o 130 o 50 o 140 o 150 o 30 o 160 o 20 o 170 o 180 o 0 o 190 o 350 o 200 o 340 o 210 o 330 o 220 o 320 o 230 o 310 o 240 o 250 o 260 o 270 o 280 o 290 o 300 o

O grau como unidade de medida 120 o 110 o 100 o 90 o 80 o 70 o 60 o 130 o 50 o 140 o 150 o 30 o 160 o 20 o 170 o 180 o 0 o 190 o 350 o 200 o 340 o 210 o 330 o 220 o 320 o 230 o 310 o 240 o 250 o 260 o 270 o 280 o 290 o 300 o

O grau como unidade de medida 120 o 110 o 100 o 90 o 80 o 70 o 60 o 130 o 50 o 140 o 150 o 30 o 160 o 20 o 170 o 180 o 0 o 190 o 1 o 350 o 200 o 340 o 210 o 330 o 220 o 320 o 230 o 310 o 240 o 250 o 260 o 270 o 280 o 290 o 300 o 1º = 1 360

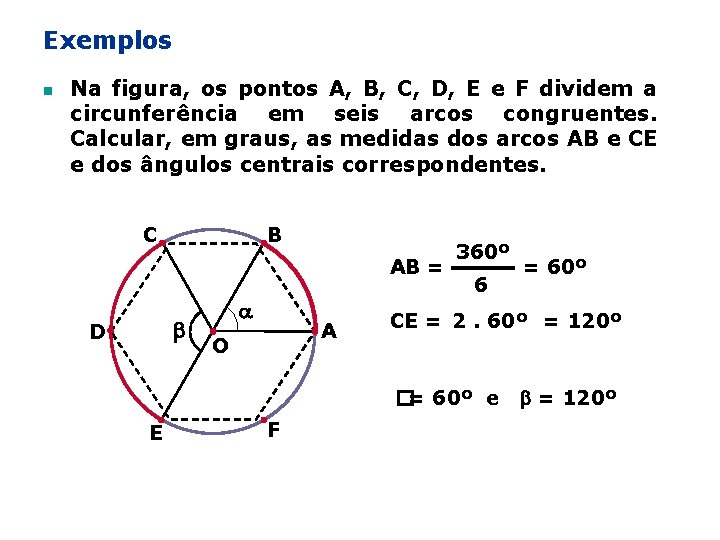
Exemplos n Na figura, os pontos A, B, C, D, E e F dividem a circunferência em seis arcos congruentes. Calcular, em graus, as medidas dos arcos AB e CE e dos ângulos centrais correspondentes. C B AB = D A O 360º 6 CE = 2. 60º = 120º �= 60º e E F = 60º = 120º

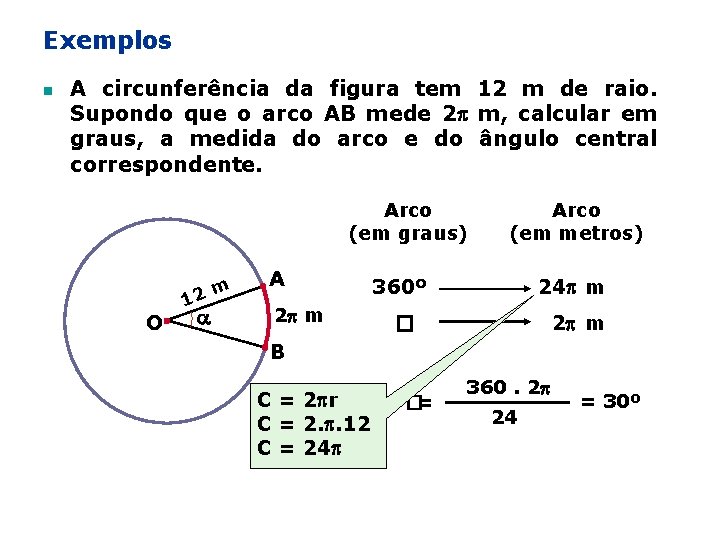
Exemplos n A circunferência da figura tem 12 m de raio. Supondo que o arco AB mede 2 m, calcular em graus, a medida do arco e do ângulo central correspondente. Arco (em graus) O m 12 A 2 m Arco (em metros) 24 m 360º 2 m � B C = 2 r C = 2. . 12 C = 24 �= 360. 2 24 = 30º

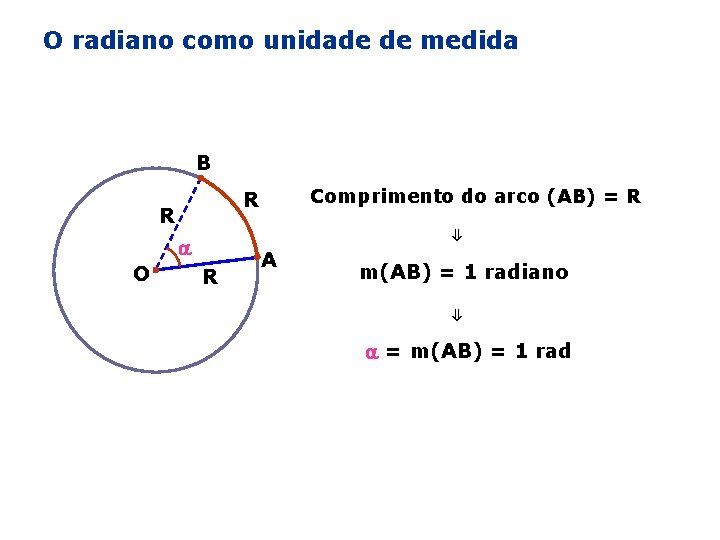
O radiano como unidade de medida B R ⇓ O Comprimento do arco (AB) = R R R A m(AB) = 1 radiano ⇓ = m(AB) = 1 rad

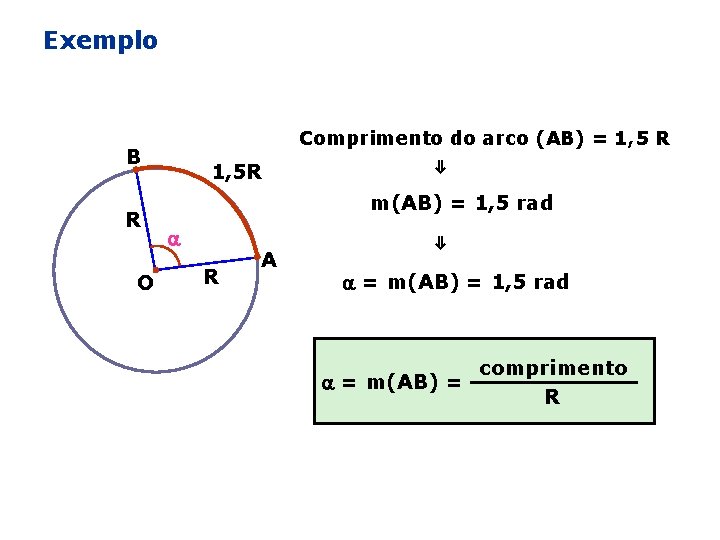
Exemplo Comprimento do arco (AB) = 1, 5 R B R O 1, 5 R ⇓ m(AB) = 1, 5 rad R A ⇓ = m(AB) = 1, 5 rad comprimento = m(AB) = R

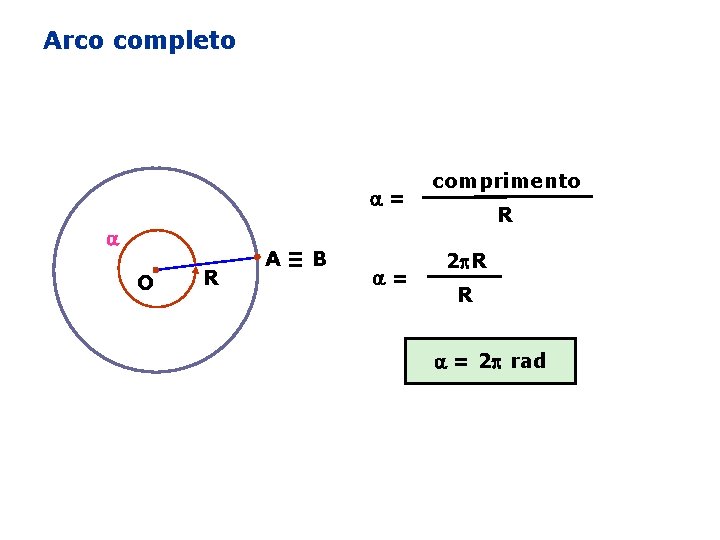
Arco completo = O R A≡B = comprimento R 2 R R = 2 rad

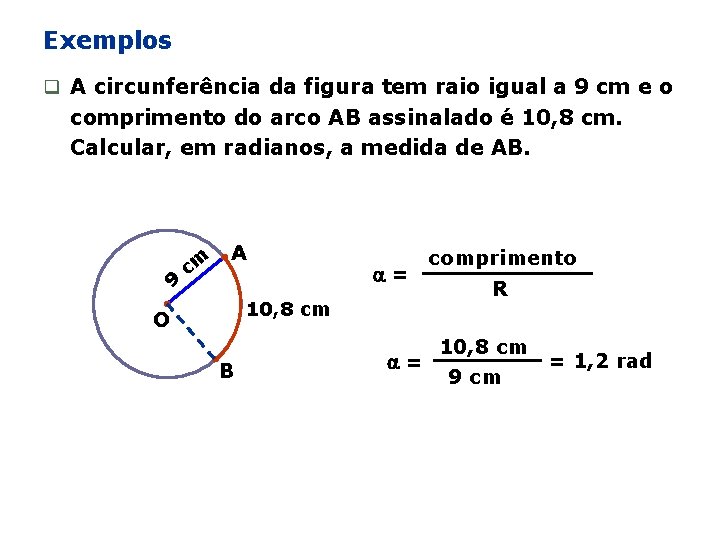
Exemplos q A circunferência da figura tem raio igual a 9 cm e o comprimento do arco AB assinalado é 10, 8 cm. Calcular, em radianos, a medida de AB. 9 cm A = 10, 8 cm O B = comprimento R 10, 8 cm 9 cm = 1, 2 rad

Exemplos q O arco AB da figura tem medida de 30º e o raio da circunferência é de 4 cm. Calcular, em cm, o comprimento do arco AB. m c O 4 ângulo A 2 R x 360º 30º B comprimento x= 2 . 4. 30 360 = 2 3 ≈ 2, 1 cm

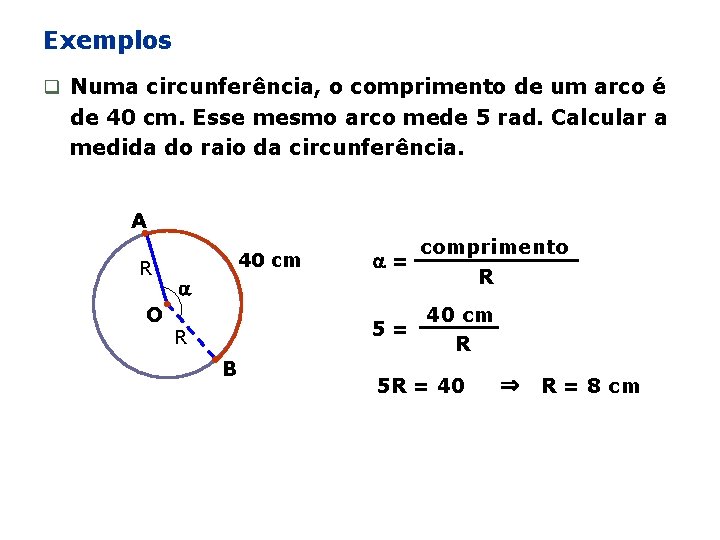
Exemplos q Numa circunferência, o comprimento de um arco é de 40 cm. Esse mesmo arco mede 5 rad. Calcular a medida do raio da circunferência. A R O 40 cm = comprimento R 5= R B 40 cm R 5 R = 40 ⇒ R = 8 cm

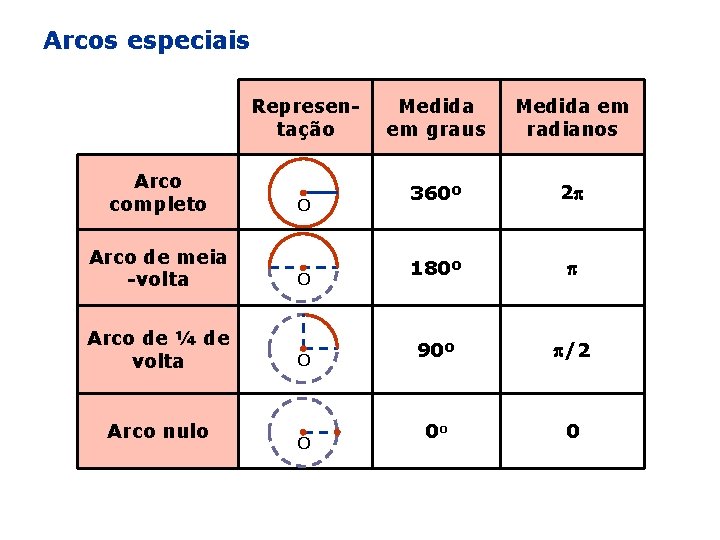
Arcos especiais Representação Arco completo O Arco de meia -volta O Arco de ¼ de volta O Arco nulo O Medida em graus Medida em radianos 360º 2 180º 90º /2 0 o 0

Transformando unidades As medidas de um arco em graus e radianos são proporcionais. Por isso podemos transformar uma unidade em outra por uma regra de três. 180º correspondem a rad

Exemplos q Transformar 72º em radianos. 180º rad 72º x x= 72. 180 = 2 rad 5

Exemplos q Exprimir 5 4 rad em graus. rad equivale a 180º. x= 5. 4 = 5. 180 4 = 225º