Trigonometra Plana Idea de ngulo Rectas que se

Trigonometría Plana

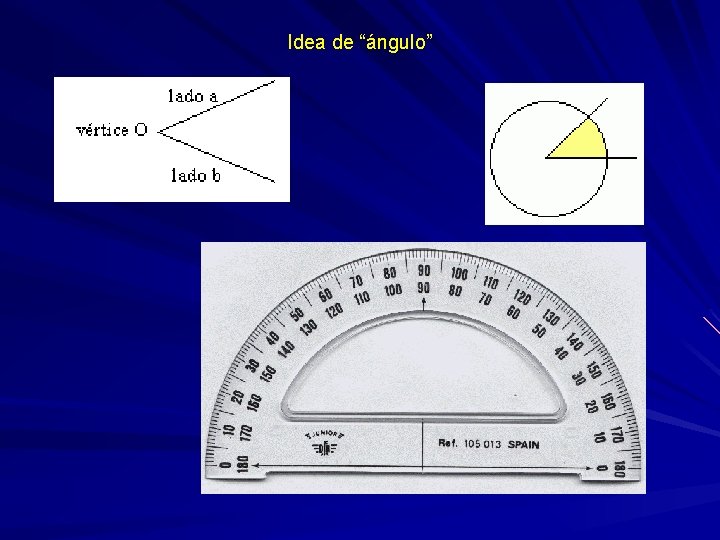
Idea de “ángulo”

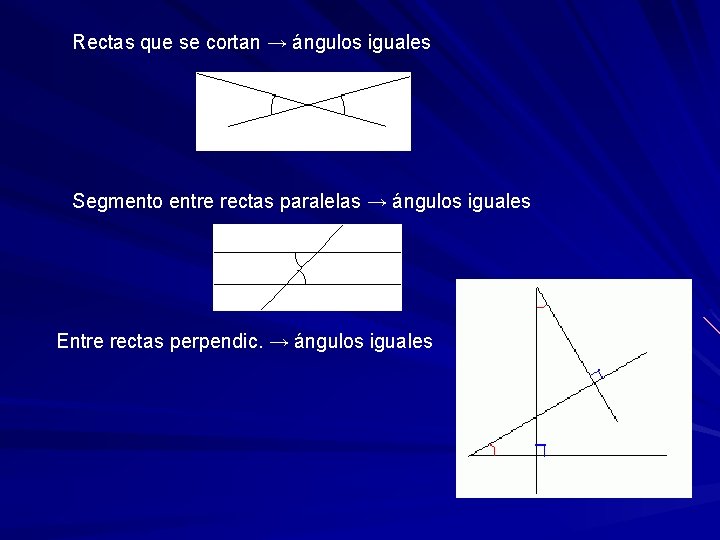
Rectas que se cortan → ángulos iguales Segmento entre rectas paralelas → ángulos iguales Entre rectas perpendic. → ángulos iguales

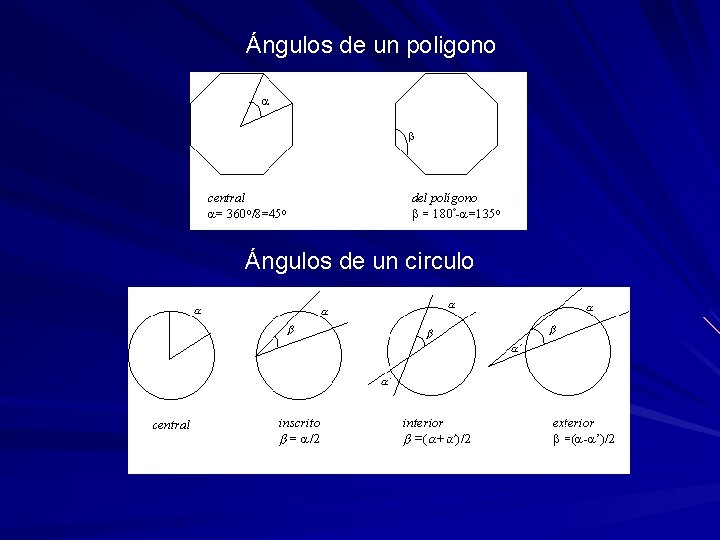
Ángulos de un poligono Ángulos de un circulo

ÁNGULOS EN RADIANES Se define el radian como el ángulo que en una circunferencia subtiende respecto del centro O un arco MN con igual longitud que el radio r. N s O r M Para una circunferencia de radio r, y un cierto ángulo α subtendiendo un arco de longitud s, el cociente s/r nos da el valor de ese ángulo en radianes.

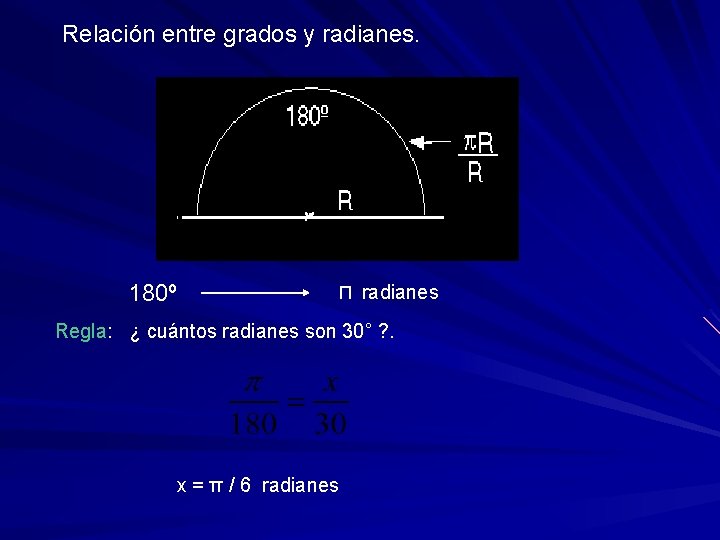
Relación entre grados y radianes. 180º Π radianes Regla: ¿ cuántos radianes son 30° ? . x = π / 6 radianes

¿ cuántos grados son 0, 357 radianes ? . * Es interesante también recordar que 1 radián son 180°/π , es decir, 57, 29. . . grados. Mientras que 1 grado son π /180° , o sea, 0, 1745. . . radianes. Propiedad importante: * puede establecerse la siguiente relación entre un ángulo α y el arco de circunferencia subtendido: s = α. R (para α en radianes)

Algunas relaciones entre ángulos y radianes: Ejemplo 1: Queremos conocer rápidamente a qué equivalen 75° , entonces: 75° = 60° + 15° π/3 + (1/2) π/6 5 π/12 Ejemplo 2: Queremos conocer rápidamente a qué equivalen 265° , entonces: 265° = 270° - 5° 3 π/2 - (1/6) π/6 53 π/36

Relaciones Circulares R. Fundamental: sin 2 α + cos 2 α = 1 Proyecciones x = R cos α y = R sin α

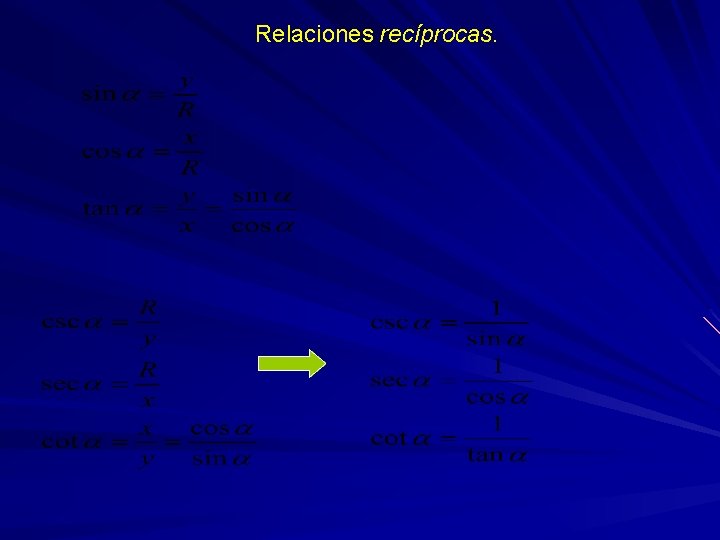
Relaciones recíprocas.

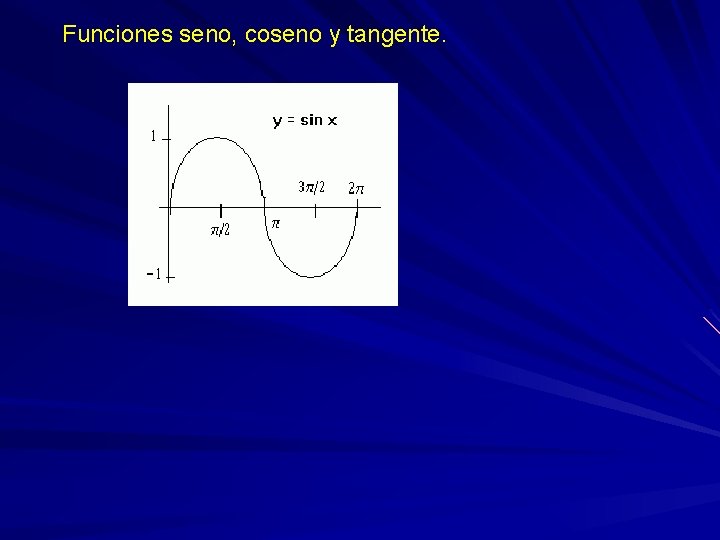
Funciones seno, coseno y tangente.

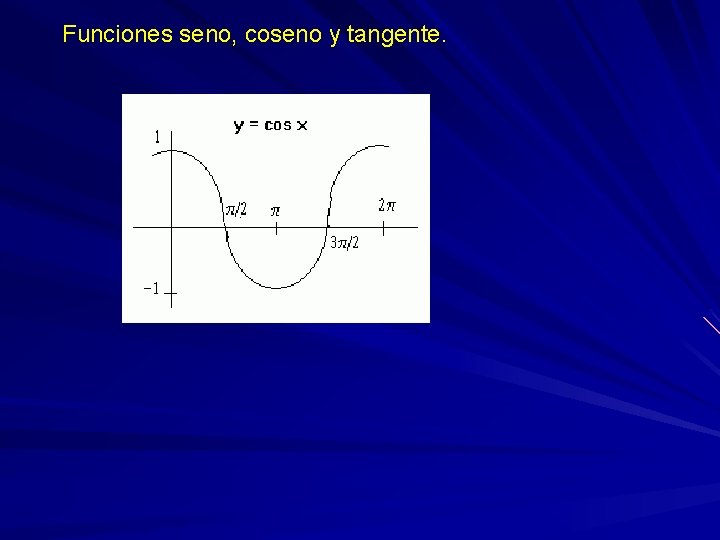
Funciones seno, coseno y tangente.

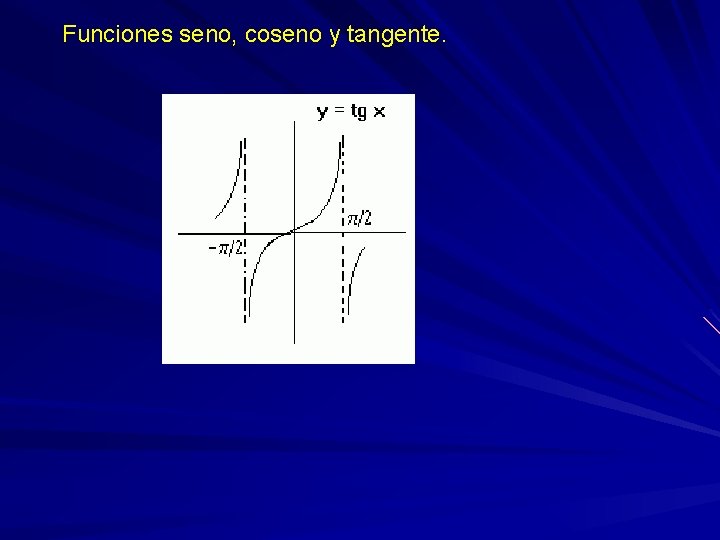
Funciones seno, coseno y tangente.

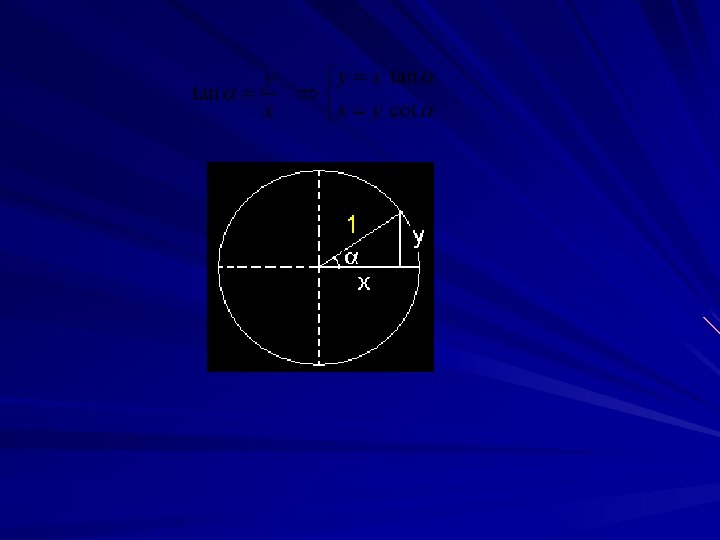
La circunferencia Trigonométrica s = α. R s = α Las relaciones circulares en la circunf. Trigonométrica sin α = y / R cos α = x / R tan α = y/x = sin α / cos α En la circ. Trig. (con R = 1): sin α = y cos α = x

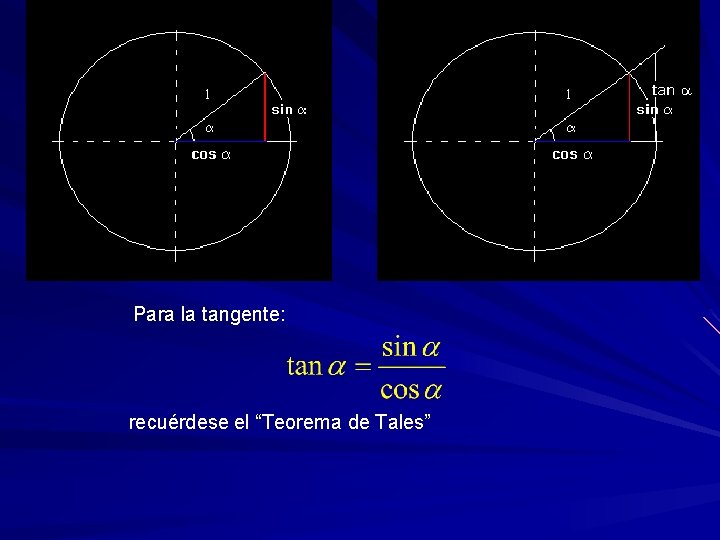
Para la tangente: recuérdese el “Teorema de Tales”

Atención: En el anterior ejemplo tanto el seno como el coseno eran positivos, pues se encuentran o bien arriba del eje horizontal, o bien a la derecha del vertical. Pero pueden darse otros casos: Para la tangente hay que ver en qué cuadrante se halla.

Este tipo de circunferencias trigonométricas sirve para hacer diversas consideraciones sobre senos y cosenos de ciertos ángulos. sin (α + π/2) = cos α cos (α + π/2) = - sin α sin (π - α ) = sin α cos ( π - α ) = - cos α

EJERCICIOS 1) Dibuje una circunferencia trigonométrica con dos ángulos a y b, siendo a pequeño y siendo b = π/2 - α (dos ángulos complementarios). Establezca las relaciones entre senos y cosenos de los ángulos complementarios. 2) Considere una circunferencia trigonométrica con dos ángulos α y β, siendo α pequeño y siendo β = α + π. Establezca las relaciones entre senos y cosenos de estos dos ángulos. 3) Sean dos ángulos α y β, siendo α pequeño y siendo β = 3π/2 -α. Establezca con la ayuda de la circunferencia trigonométrica las relaciones entre senos y cosenos de estos dos ángulos. 4) Sean dos ángulos α y β, siendo α pequeño y siendo β = -α (también puede expresarse β = 2π - α). Establezca con la ayuda de la circunferencia trigonométrica las relaciones entre senos y cosenos de estos dos ángulos.

Relación fundamental

Razones trigonométricas de la suma Razones trigonométricas de la resta

Razones del ángulo doble Razones del ángulo mitad

Suma y resta de razones trigon.