Tries Fredkin CACM 1960 Compacted Trie Performance 0

Tries

[Fredkin, CACM 1960] (Compacted) Trie Performance: 0 • Search ≈ O(|P|) time • Space ≈ O(K + N) 1 y 2 stile zyg (2; 3, 5) 5 1 etic ial 2 3 s z aibelyite 2 omo 7 5 czecin ygy 4 systile syzygetic syzygial syzygy 6 szaibelyite szczecin szomo

[Fredkin, CACM 1960] (Compacted) Trie Performance: 0 • Search ≈ O(|P|) time • Space ≈ O(K + N) 1 y . . . But in practice… 2 • Search: random memory accesses stile • Space: len + pointers + strings zyg (2; 3, 5) 5 1 etic ial 2 3 s z aibelyite 2 omo 7 5 czecin ygy 4 systile syzygetic syzygial syzygy 6 szaibelyite szczecin szomo

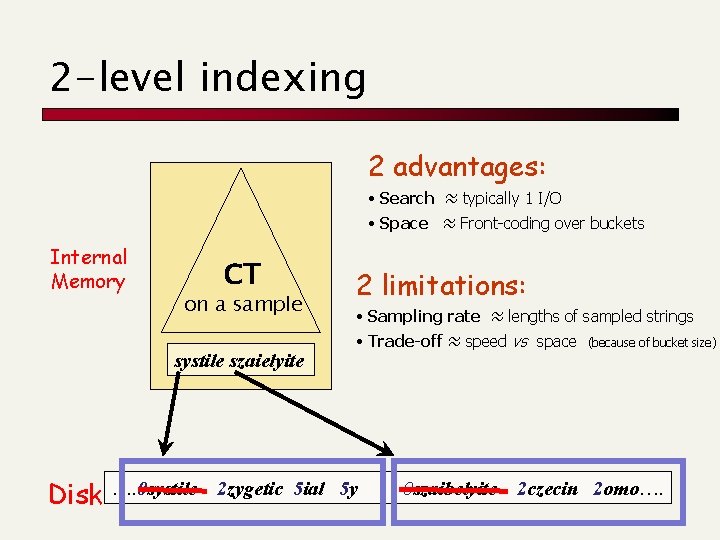
2 -level indexing 2 advantages: • Search ≈ typically 1 I/O • Space ≈ Front-coding over buckets Internal Memory CT on a sample systile szaielyite Disk …. 0 systile 2 limitations: • Sampling rate ≈ lengths of sampled strings • Trade-off ≈ speed vs space 2 zygetic 5 ial 5 y 0 szaibelyite (because of bucket size) 2 czecin 2 omo….

[Morrison, J. ACM 1968] An old idea: Patricia Trie 0 1 y 2 stile zyg etic 2 3 2 omo 7 5 ygy ial z aibelyite 5 1 s 4 czecin 6

[Ferragina-Grossi, J. ACM 1999] A new search 0 Search(P): • Phase 1: tree navigation • Phase 2: Compute LCP • Phase 3: tree navigation y 1 2 s 5 z g < ya z Three-phase search: P = syzyyea s P’s position 2 0 1 2 o 5 c Only 1 string ise checked y i Trie Space ≈ #strings, NOT their length …. systile syzygetic syzygial syzygy szaibelyite szczecin szomo….

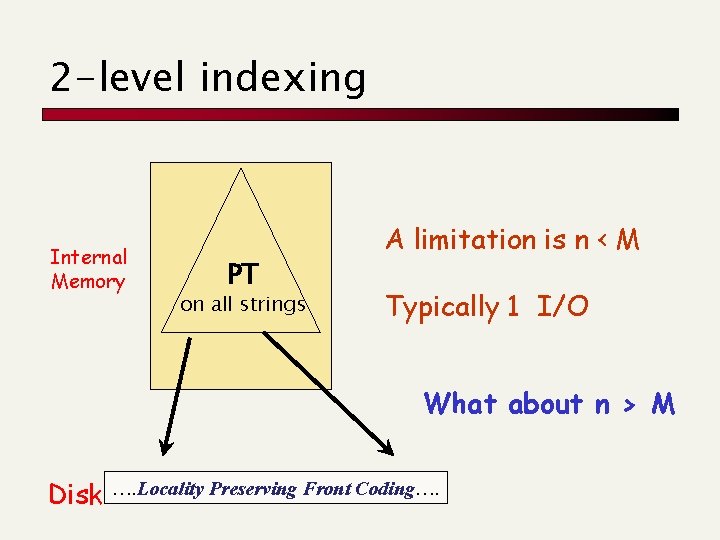
2 -level indexing Internal Memory PT on all strings A limitation is n < M Typically 1 I/O What about n > M Disk …. Locality Preserving Front Coding….

[Ferragina-Grossi, J. ACM 1999] The String B-tree + Search(P) • O((p/B) log. B n) I/Os • O(occ/B) I/Os 1 string checked : O(p/B) PT 29 13 20 18 3 O(log. B n) levels 23 It is dynamic. . . PT 29 2 PT 26 13 PT 29 1 9 20 25 PT 5 2 26 10 4 PT 6 PT 7 13 Lexicographic position of P 20 16 28 18 3 14 PT 8 25 6 12 15 22 18 21 23 PT 3 27 24 11 PT 14 21 17 23 Knuth, vol 3°, pag. 489: “elegant”

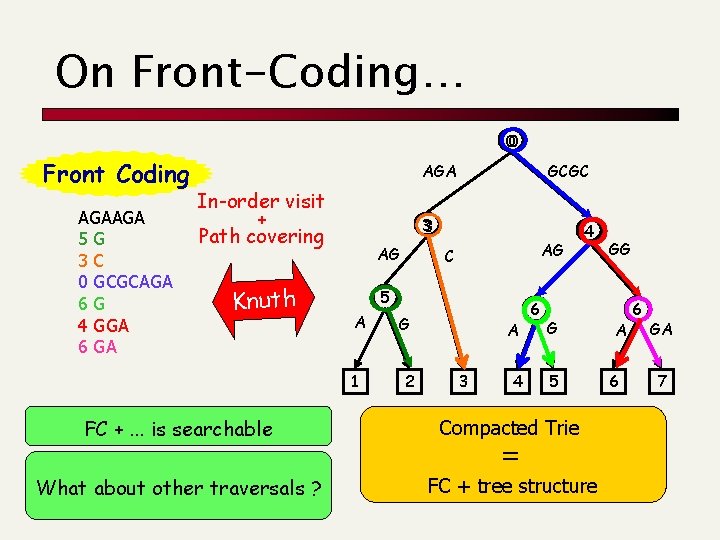
On Front-Coding… 00 Front Coding AGAAGA 5 G 3 C 0 GCGCAGA 6 G 4 GGA 6 GA AGA In-order visit + Path covering Knuth GCGC 3 3 AG AG C 5 A 1 G 2 A 3 4 6 4 G 5 FC +. . . is searchable Compacted Trie What about other traversals ? FC + tree structure = GG A 6 6 GA 7

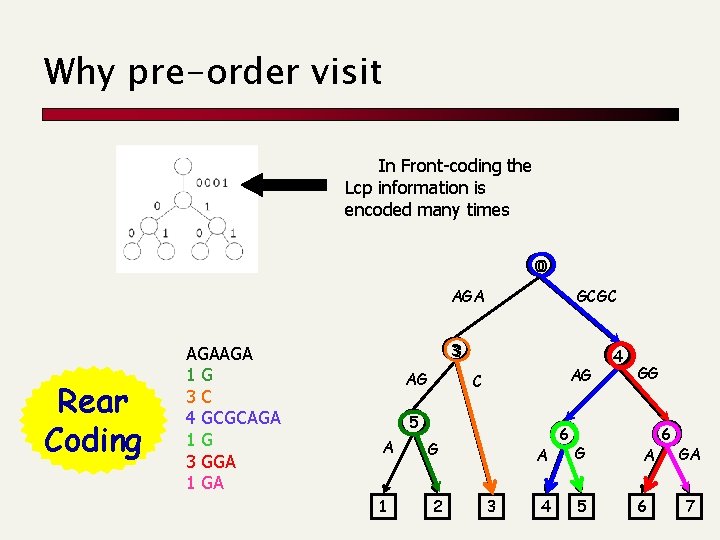
Why pre-order visit In Front-coding the Lcp information is encoded many times 00 AGA Rear Coding AGAAGA 1 G 3 C 4 GCGCAGA 1 G 3 GGA 1 GA GCGC 3 3 AG AG C 5 A 1 G 2 A 3 4 6 G 5 4 GG A 6 6 GA 7

Text Indexing

What do we mean by “Indexing” ? q Word-based indexes, here a notion of “word” must be devised ! » Inverted lists, Signature files, Bitmaps. q Full-text indexes, no constraint on text and queries ! » Suffix Array, Suffix tree, String B-tree, . . .

Basic notation and facts Pattern P occurs at position i of T iff P is a prefix of the i-th suffix of T (ie. T[i, N]) i P T T[i, N] Occurrences of P in T = All suffixes of T having P as a prefix P = si T = mississippi 4, 7 SUF(T) = Sorted set of suffixes of T Reduction From substring search To prefix search

The Suffix Tree # ssi T# = mississippi# 2 4 6 8 10 2 i 2 1 ppi# i# 3 ppi# 7 1 10 pi# 5 si i# pp 8 p ssi ppi# ssippi# 11 4 1 ssip ppi# Maximal repeated substring = node mississippi# 1 # Search pattern P s i 12 Space: #nodes 0 6 3 4 9 Label = <pos, len>

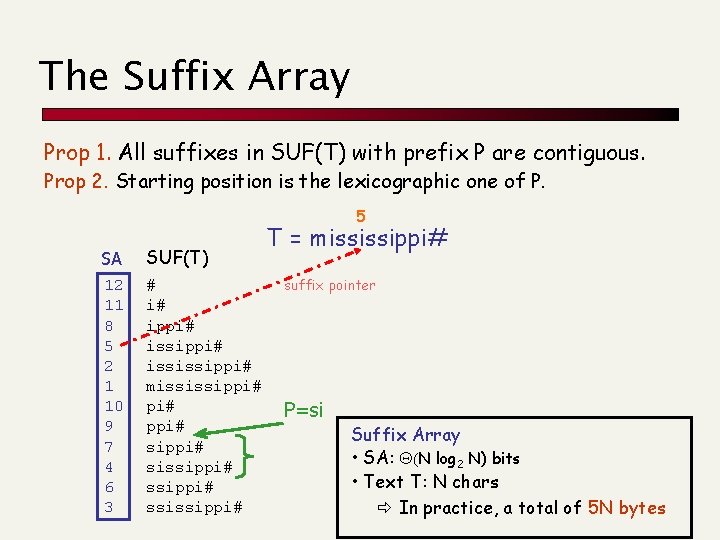
The Suffix Array Prop 1. All suffixes in SUF(T) with prefix P are contiguous. Prop 2. Starting position is the lexicographic one of P. 5 SA SUF(T) 12 11 8 5 2 1 10 9 7 4 6 3 # i# ippi# ississippi# mississippi# sissippi# ssissippi# T = mississippi# suffix pointer P=si Suffix Array • SA: Q(N log 2 N) bits • Text T: N chars In practice, a total of 5 N bytes

Searching a pattern Indirected binary search on SA: O(p) time per suffix cmp SA 12 11 8 5 2 1 10 9 7 4 6 3 T = mississippi# P is larger 2 accesses per step P = si

Searching a pattern Indirected binary search on SA: O(p) time per suffix cmp SA 12 11 8 5 2 1 10 9 7 4 6 3 T = mississippi# P is smaller P = si Suffix Array search • O(log 2 N) binary-search steps • Each step takes O(p) char cmp overall, O(p log 2 N) time + [Manber-Myers, ’ 90]

Locating the occurrences SA occ=2 T = mississippi# 12 11 8 5 where 2 1 10 si# 9 7 sippi 4 sissippi 6 3 si$ 4 7 Suffix Array search • O (p + log 2 N + occ) time #< S<$

Text mining Lcp[1, N-1] = longest-common-prefix between suffixes adjacent in SA Lcp 0 1 1 4 0 0 1 0 2 1 3 SA • How long is the common prefix between T[i, . . . ] and T[j, . . . ] ? 12 # • Min of the subarray Lcp[h, k-1] s. t. SA[h]=i and SA[k]=j i# 11 8 ippi# 5 issippi# 2 ississippi# 1 mississippi 10 pi# 9 ppi# 7 sippi# 4 sissippi# 6 ssippi# 3 ssissippi# Lcp(7, 3) = 1 = min{2, 1, 3}

Text mining Lcp[1, N-1] = longest-common-prefix between suffixes adjacent in SA Lcp 0 1 1 4 0 0 1 0 2 1 3 SA 12 # • Does it exist a repeated substring of length ≥ L ? • Maximal Lcp of a suffix is with its adjacent i# 11 8 ippi# • Search for Lcp[i] ≥ L 5 issippi# 2 ississippi# 1 mississippi 10 pi# 9 ppi# 7 sippi# 4 sissippi# 6 ssippi# 3 ssissippi#

Text mining Lcp[1, N-1] = longest-common-prefix between suffixes adjacent in SA Does exist a substring of length ≥ L occurring ≥ C times ? Lcp 0 1 1 4 0 0 1 0 2 1 3 SA 12 # 11 8 5 2 1 10 9 7 4 6 3 • Exist ≥ C equal substrings of length ≥ L chars i# • Exist ≥ C suffixes sharing a prefix of ≥ L chars ippi# issippi# • These suffixes may be not contiguous, but. . . ississippi# mississippi • Their “block” has a common prefix of ≥ L chars pi# • Search for Lcp[i, i+C-2] whose entries are ≥ L ppi# sissippi# ssissippi# L = 1, C = 4

How to construct SA from T ? SA 12 # 11 8 5 2 1 10 9 7 4 6 3 i# ippi# ississippi# mississippi pi# ppi# sissippi# ssissippi# Elegant but inefficient Input: T = mississippi# Obvious inefficiencies: • Q(n 2 log n) time in the worst-case • Q(n log n) cache misses or I/O faults

T(n) = O(split) + T(2 n/3) + O(|S 1|) + O(merge) = O(n) The skew algorithm n The key problem: Compare efficiently two suffixes n Brute-force = Q(n) time per cmp, Q(n 2 log n) total In order to sort the suffixes of S 1. Divide the suffixes of S in two groups n n S 0, 2 = suffixes starting at positions 0 mod 3 or 2 mod 3 S 1 = suffixes starting at positions 1 mod 3 2 a. Sort recursively S 0, 2 (they are 2 n/3) 2 b. Sort S 1: suffix(3 i+1) = S[3 i+1] suff(3 i+2) 3. Merge the sorted S 0, 2 with the sorted S 1

Sort recursively S 0, 2 We turn this problem into the SA-construction of a shorter string of length (2/3)n. 1 2 3 4 5 6 7 8 9 10 11 12 13 S=AAT GTG AGA TGA $$$ n n Radix. Sort all triplets that start at positions 0, 2 mod 3 n T = {ATG, TGT, TGA, GAG, GAT, ATG, GA$, A$$} n Sort(T) = (A$$, ATG, GA$, GAG, GAT, TGA, TGT) Assign lexicographic names (log n bits) n n A$$=1, ATG=2, GA$=3, … Build s 0, 2 and encode it: n n ATG TGA GAT GA$ TGT GAG ATG A$$ 2 6 5 3 7 4 2 1

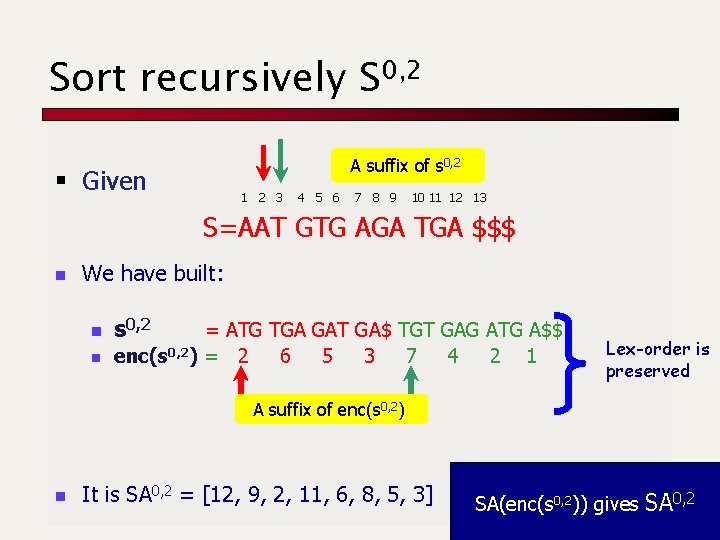
Sort recursively S 0, 2 A suffix of s 0, 2 § Given 1 2 3 4 5 6 7 8 9 10 11 12 13 S=AAT GTG AGA TGA $$$ n We have built: n n s 0, 2 = ATG TGA GAT GA$ TGT GAG ATG A$$ enc(s 0, 2) = 2 6 5 3 7 4 2 1 Lex-order is preserved A suffix of enc(s 0, 2) n It is SA 0, 2 = [12, 9, 2, 11, 6, 8, 5, 3] SA(enc(s 0, 2)) gives SA 0, 2

Sort S 1 We turn this problem into the sort of pairs Suffix of S 1 1 2 3 4 5 6 7 8 9 10 11 12 13 S=AAT GTG AGA TGA $$$ Key observation: suff(1) = <A, pos(2)> = <A, 3> suff(7) = <A, pos(8)> = <A, 6> SA 0, 2 = [12, 9, 2, 11, 6, 8, 5, 3] SA 1 = [1, 7, 4, 10]

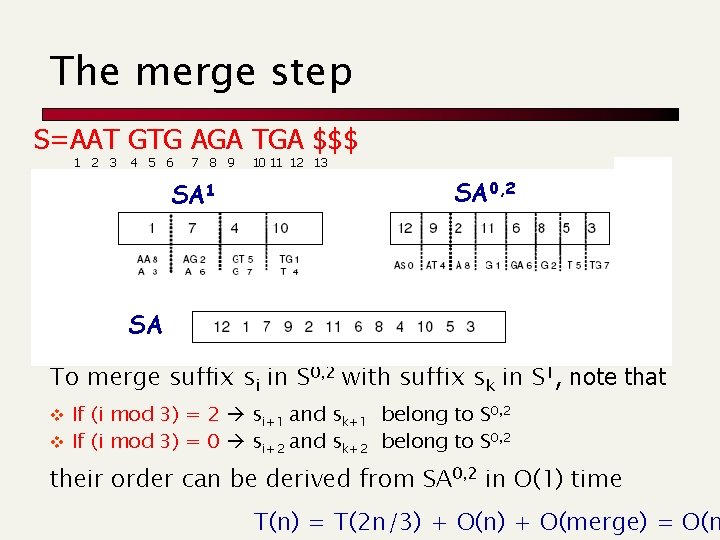
The merge step S=AAT GTG AGA TGA $$$ 1 2 3 4 5 6 7 8 9 SA 1 10 11 12 13 SA 0, 2 SA To merge suffix si in S 0, 2 with suffix sk in S 1, note that v If (i mod 3) = 2 si+1 and sk+1 belong to S 0, 2 v If (i mod 3) = 0 si+2 and sk+2 belong to S 0, 2 their order can be derived from SA 0, 2 in O(1) time T(n) = T(2 n/3) + O(n) + O(merge) = O(n