Tries and Digital Search Trees Tries 1 Tries

Tries and Digital Search Trees Tries - 1

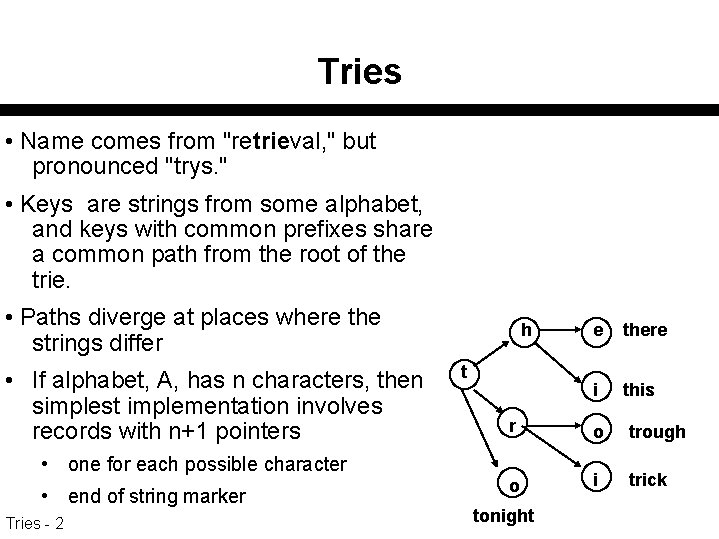
Tries • Name comes from "retrieval, " but pronounced "trys. " • Keys are strings from some alphabet, and keys with common prefixes share a common path from the root of the trie. • Paths diverge at places where the strings differ • If alphabet, A, has n characters, then simplest implementation involves records with n+1 pointers • one for each possible character • end of string marker Tries - 2 h t e there i this r o trough o i trick tonight

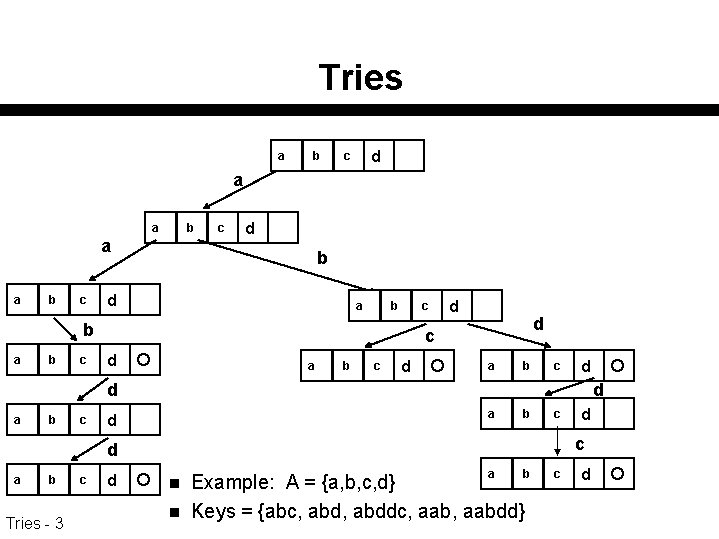
Tries a b d c a a b c c d b d a b c b a b c d d c d a b c d a d b c c d a b Tries - 3 c d d n n a b Example: A = {a, b, c, d} Keys = {abc, abddc, aabdd} c d

Tries n n If all words are equally likely to occur, the average number of letters we need to inspect to distinguish the query can be less than for a binary search tree. Number of characters examined during a random search is logm. N for nodes with m links and N random keys stored in the trie. h t Tries - 4 e there i this r o trough o i trick

Issues n How do we store the set of nonempty links at a node? n Is there some way to compress the trie? – For example, nodes in the trie with only one non-empty link add no information and slow down search Tries - 5

Issues n Strings are sequences of characters, so it made sense to branch on characters, but what about arbitrary bit strings? – Each level of the trie can branch on a single bit – digital search tries – But generally, we could branch on any number of k bits Tries - 6

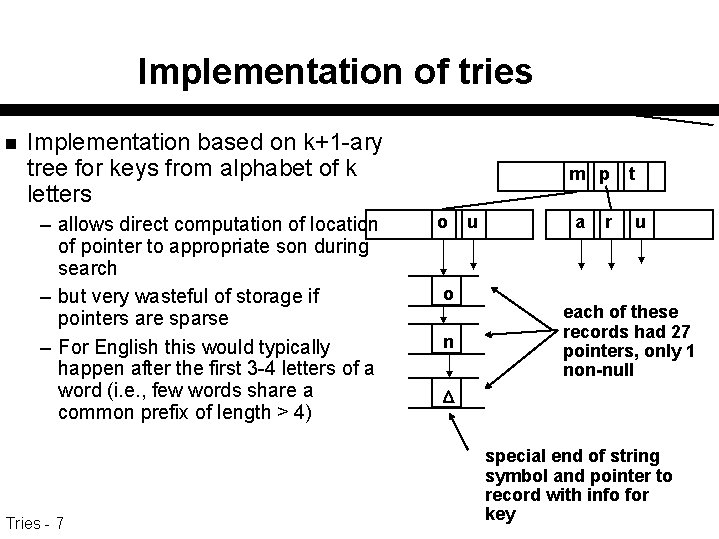
Implementation of tries n Implementation based on k+1 -ary tree for keys from alphabet of k letters – allows direct computation of location of pointer to appropriate son during search – but very wasteful of storage if pointers are sparse – For English this would typically happen after the first 3 -4 letters of a word (i. e. , few words share a common prefix of length > 4) Tries - 7 m p o o n u a r t u each of these records had 27 pointers, only 1 non-null special end of string symbol and pointer to record with info for key

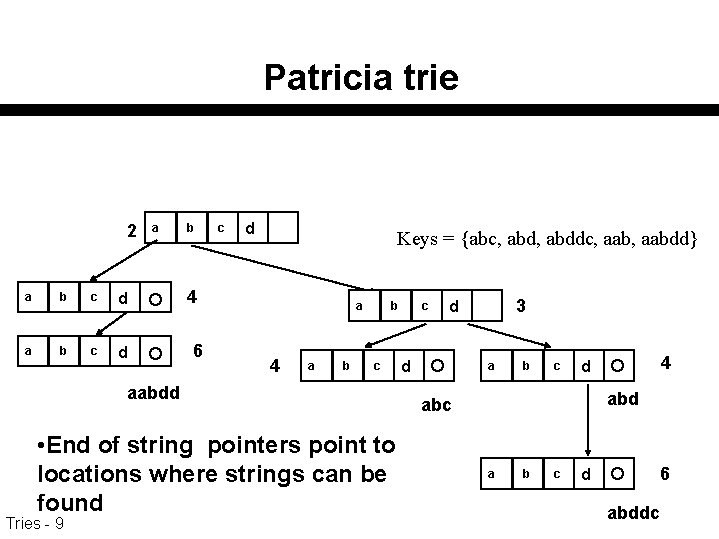
Patricia Trees Practical algorithm to retrieve information coded in alphanumeric n Eliminate nodes with only one nonempty child n Store with each node the index of the character position on which that node discriminates n – When lookup encounters a node labeled i and the i'th character of the search key is the j'th possible symbol, follow the j'th pointer from that node – if the search key has fewer than i characters, it is not in the trie. n Key is no longer uniquely determined by path, so must store key itself at an end of path field Tries - 8

Patricia trie 2 a b c d Keys = {abc, abddc, aabdd} 4 6 a 4 a b b c aabdd • End of string pointers point to locations where strings can be found Tries - 9 c 3 d d a b c 4 d abc a b c 6 d abddc

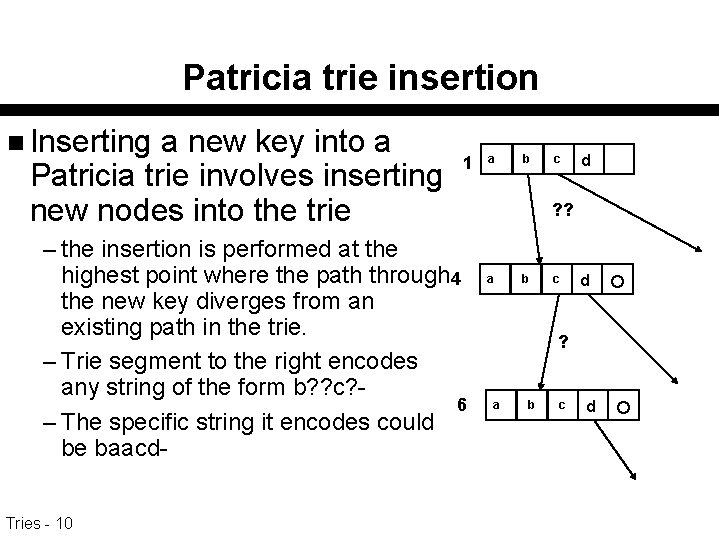
Patricia trie insertion n Inserting a new key into a Patricia trie involves inserting new nodes into the trie 1 – the insertion is performed at the highest point where the path through 4 the new key diverges from an existing path in the trie. – Trie segment to the right encodes any string of the form b? ? c? 6 – The specific string it encodes could be baacd. Tries - 10 a b c d ? ? a b c d

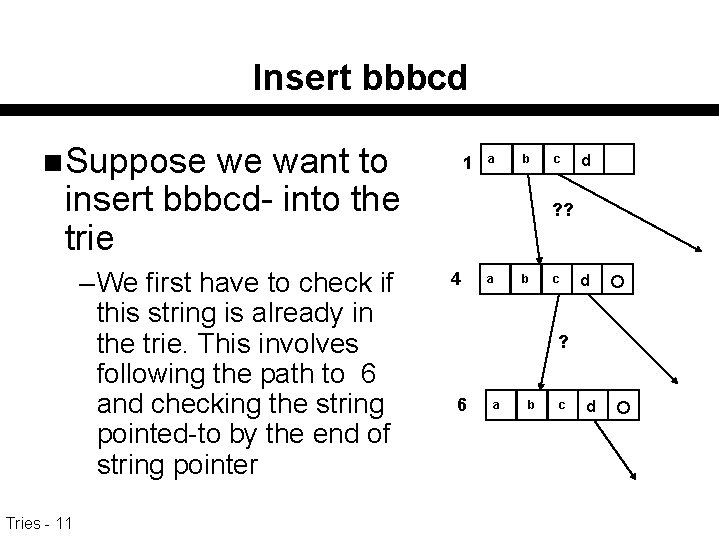
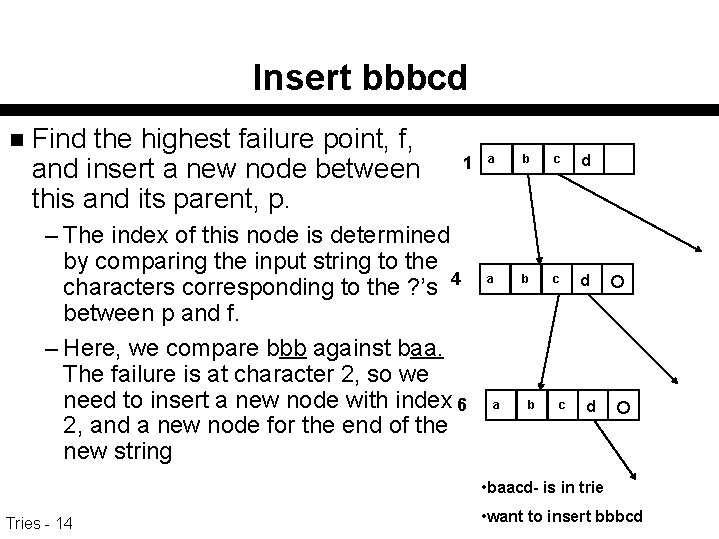
Insert bbbcd n Suppose we want to insert bbbcd- into the trie – We first have to check if this string is already in the trie. This involves following the path to 6 and checking the string pointed-to by the end of string pointer Tries - 11 1 a b c d ? ? 4 a b c d ? 6 a b c d

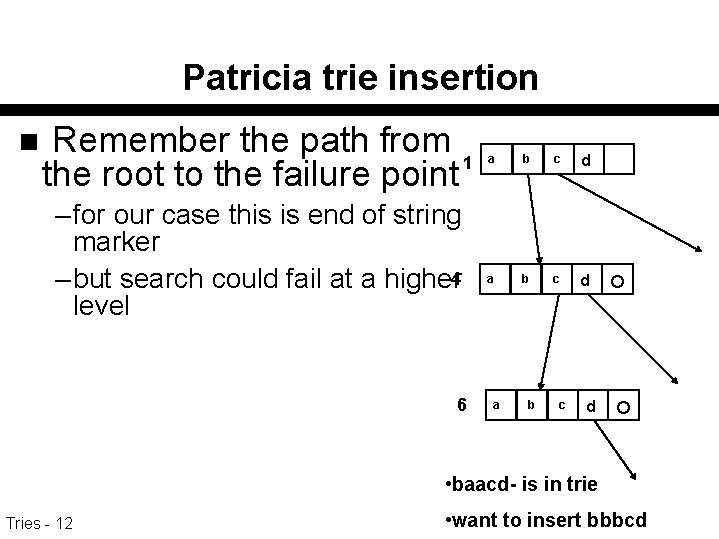
Patricia trie insertion n Remember the path from 1 the root to the failure point – for our case this is end of string marker – but search could fail at a higher 4 level 6 a b c d • baacd- is in trie Tries - 12 • want to insert bbbcd

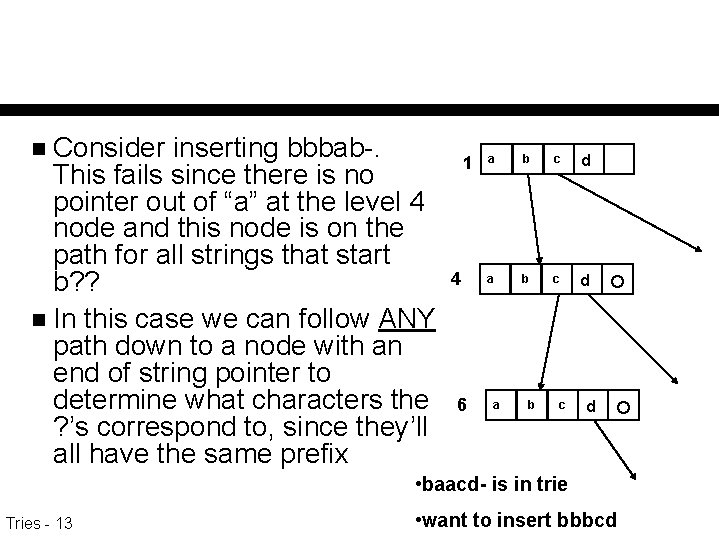
Consider inserting bbbab-. This fails since there is no pointer out of “a” at the level 4 node and this node is on the path for all strings that start b? ? n In this case we can follow ANY path down to a node with an end of string pointer to determine what characters the ? ’s correspond to, since they’ll all have the same prefix n 1 4 6 a b c d • baacd- is in trie Tries - 13 • want to insert bbbcd

Insert bbbcd n Find the highest failure point, f, and insert a new node between this and its parent, p. 1 – The index of this node is determined by comparing the input string to the characters corresponding to the ? ’s 4 between p and f. – Here, we compare bbb against baa. The failure is at character 2, so we need to insert a new node with index 6 2, and a new node for the end of the new string a b c d • baacd- is in trie Tries - 14 • want to insert bbbcd

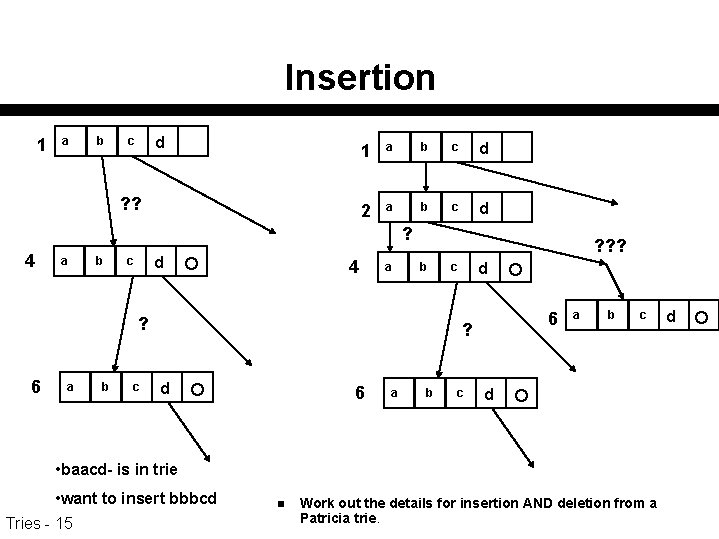
Insertion 1 a b d c ? ? 1 a b c d 2 a b c d ? 4 a b d c 4 a ? ? ? b ? 6 a b c d c 6 ? d 6 a b c d • baacd- is in trie • want to insert bbbcd Tries - 15 n Work out the details for insertion AND deletion from a Patricia trie. d

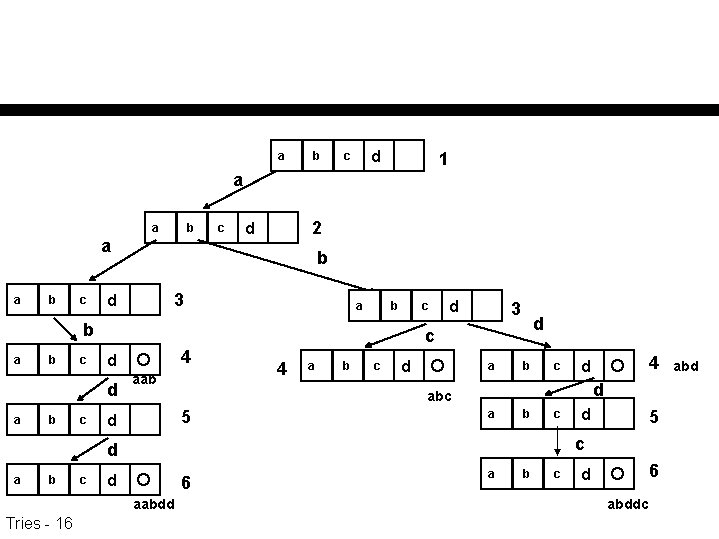
a b d c 1 a a b c c 2 d b 3 d a b c b c 3 d c 4 d d aab 4 a b c d abc 5 d a b c d 6 aabdd Tries - 16 d 5 c d a 4 d a b c 6 d abddc abd

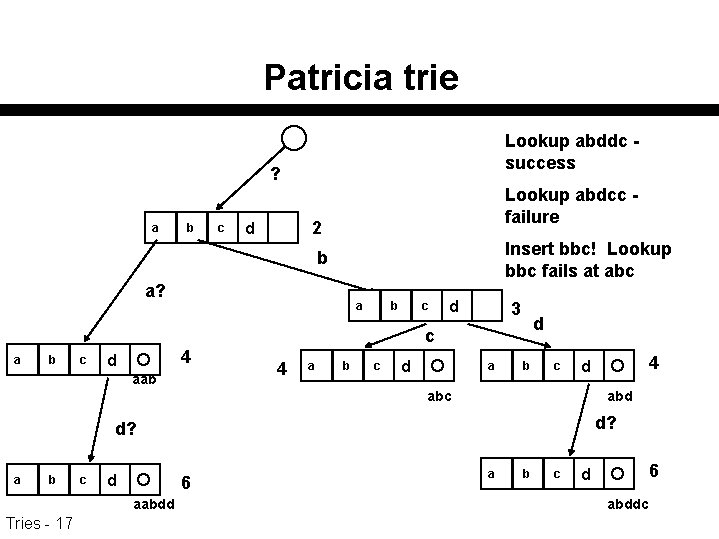
Patricia trie Lookup abddc success ? a b c Lookup abdcc failure 2 d Insert bbc! Lookup bbc fails at abc b a? a b c d 3 d c a b c 4 d aab 4 a b c d a b c abd d? a b c d 6 aabdd Tries - 17 4 d a b c 6 d abddc

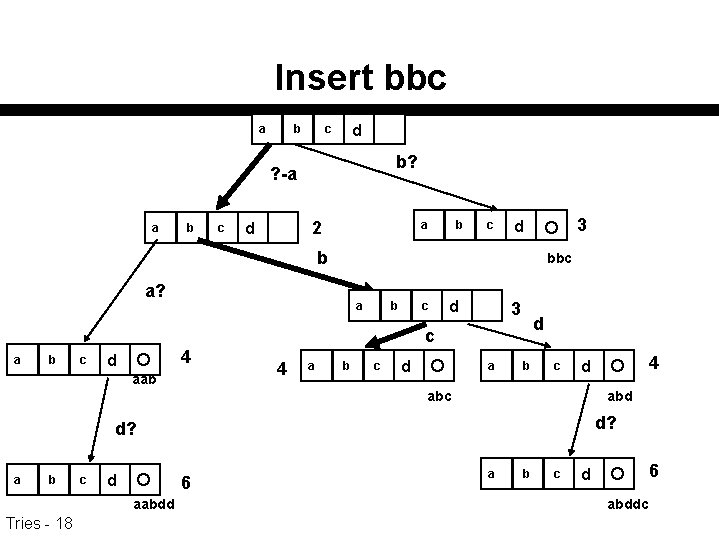
Insert bbc a b d c b? ? -a a b c 2 d a b c 3 d b bbc a? a b c d 3 d c a b c 4 d aab 4 a b c d a b c abd d? a b c d 6 aabdd Tries - 18 4 d a b c 6 d abddc

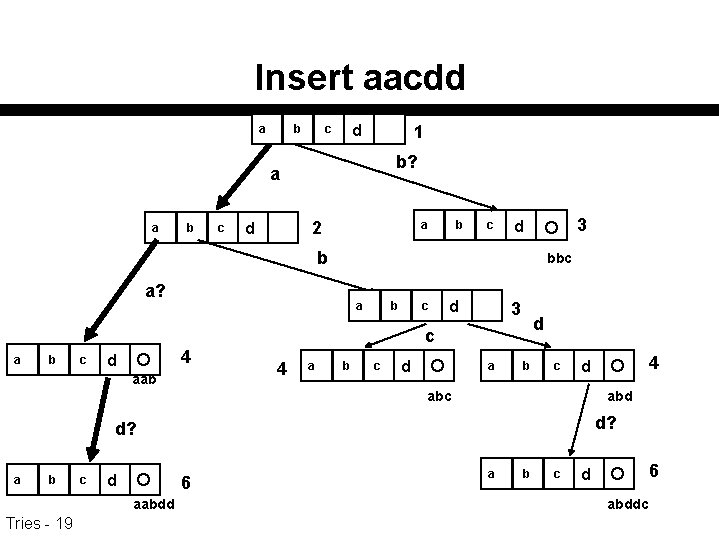
Insert aacdd a b d c 1 b? a a b c 2 d a b c 3 d b bbc a? a b c d 3 d c a b c 4 d aab 4 a b c d a b c abd d? a b c d 6 aabdd Tries - 19 4 d a b c 6 d abddc

de la Briandais tries n Use a linked list to represent a node rather than a table. – So, a node is a linked list of character/pointer pairs n Time to search a single node rises, since we have to traverse the linked list – But if nodes have only a few pointers, savings in memory can be large n Can also use Patricia tree trick, and not represent nodes having only one child Tries - 20

Tries and Web Search Engines n n n The index of a search engine (collection of all searchable words) is stored into a compressed trie Each leaf of the trie is associated with a word and has a list of pages (URLs) containing that word, called occurrence list The trie is kept in internal memory The occurrence lists are kept in external memory and are ranked by relevance Boolean queries for sets of words (e. g. , Java and coffee) correspond to set operations (e. g. , intersection) on the occurrence lists Additional information retrieval techniques are used, such as – stopword elimination (e. g. , ignore “the” “a” “is”) – stemming (e. g. , identify “add” “adding” “added”) – link analysis (recognize authoritative pages) Tries - 21

Tries and Internet Routers n n n n Computers on the internet (hosts) are identified by a unique 32 -bit IP (internet protocol) address, usually written in “dotted-quad-decimal” notation E. g. , www. cs. brown. edu is 128. 148. 32. 110 An organization uses a subset of IP addresses with the same prefix, e. g. , Brown uses 128. 148. *. *, Yale uses 130. 132. *. * Data is sent to a host by fragmenting it into packets. Each packet carries the IP address of its destination. The internet is composed of nodes which are routers, and edges which are communication links. A router forwards packets to its neighbors using IP prefix matching rules. E. g. , a packet with IP prefix 128. 148. should be forwarded to the Brown gateway router. Routers use tries on the alphabet 0, 1 to do prefix matching. Tries - 22

Digital search trees n Treat a key as a bit string - i. e. , use an alphabet having k=2. n Creates a binary trie in which search is directed left or right depending on the next bit of the key. Each node also contains one of the keys that begins with the bit string determined by the search path to that node – that is the end of string node for that key Tries - 23 n

Digital search trees n Before search goes left or right, compare the search key against the key stored in the node. – Search will work independently of which keys are stored at which nodes, but if "common" keys are placed high in the tree, search will generally be faster – root contains most common key – its left son contains most common key beginning with 0. Tries - 24

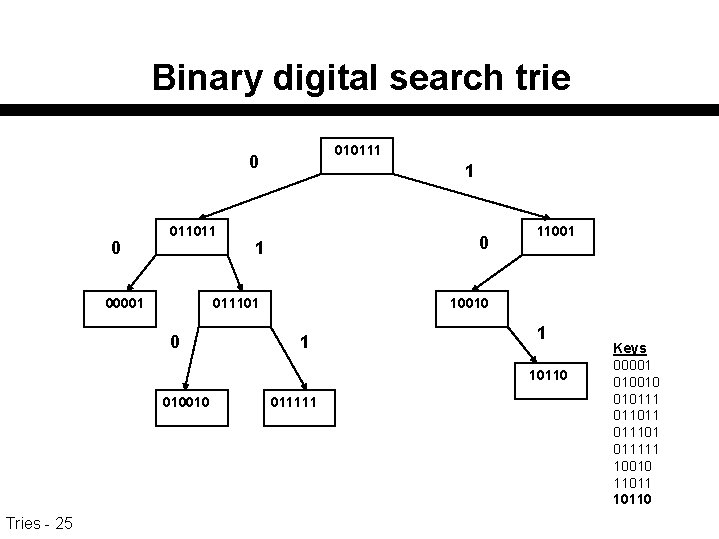
Binary digital search trie 010111 0 0 011011 00001 1 011101 0 110010 1 1 10110 010010 Tries - 25 011111 Keys 00001 010010 010111 011011 011101 011111 10010 110110

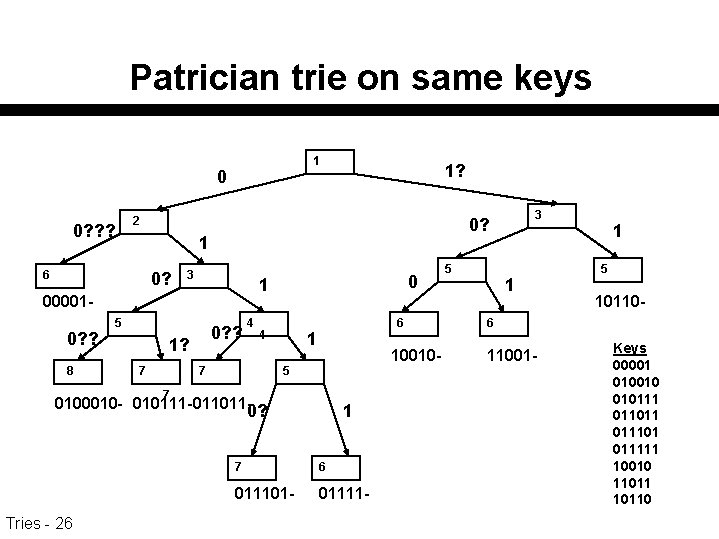
Patrician trie on same keys 1 0 0? ? ? 2 0? 3 00001 - 8 0? ? 1? 7 0 1 5 4 4 7 6 1 10010 - 5 7 0100010 - 010111 - 011011 -0? Tries - 26 3 0? 1 6 0? ? 1 7 6 011101 - 01111 - 5 1 1 5 10110 - 6 11001 - Keys 00001 010010 010111 011011 011101 011111 10010 110110

Insertion and deletion in digital search tries n Insertion – Lookup node » If lookup fails at a null pointer, insert as the appropriate child of the node at which the null pointer was encountered. » Otherwise, replace the key at which lookup fails with key to be inserted, and insert that key into the subtree rooted at that node. Tries - 27

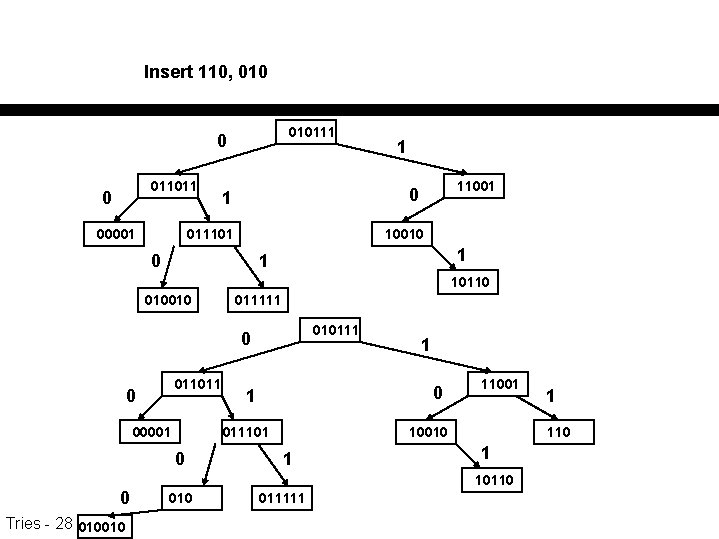
Insert 110, 010111 0 011011 0 00001 1 11001 0 1 011101 10010 0 1 1 10110 010010 011111 010111 0 011011 0 00001 0 Tries - 28 010010 0 1 011101 0 1 110010 1 10110 011111 1

Deletion n. Lookup the key to be deleted n. Replace it with a key stored at any leaf node in the subtree rooted at that node –All keys stored in the subtree have the same prefix, so can be moved up the tree to the deletion point. Tries - 29

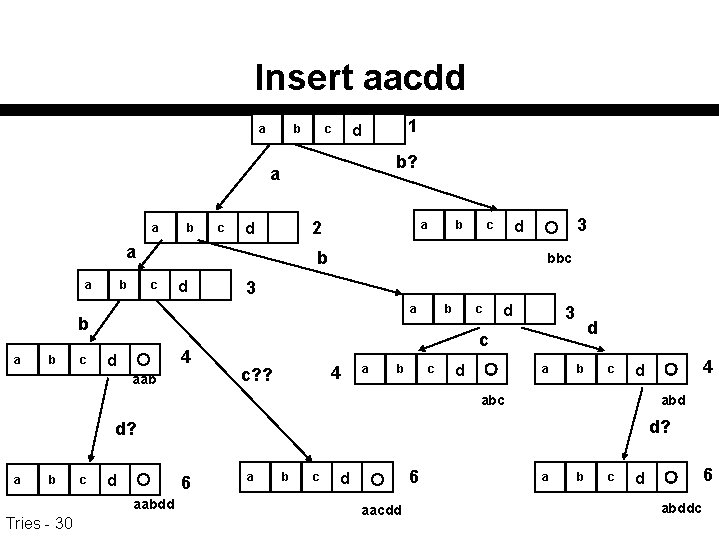
Insert aacdd a b b? a a b c 2 d a a a b c 3 a 4 d aab 3 d c bbc b a b b c d a? b 1 d c b c d 3 d c 4 c? ? a b c d a b c abd d? a b c d 6 aabdd Tries - 30 4 d a b c 6 d aacdd a b c 6 d abddc