Triaxial shapes in the sd and fp shell

Triaxial shapes in the sd and fp shell nuclei with realistic shell model Hamiltonians Zao-Chun Gao(高早春) China Institute of Atomic Energy Mihai Horoi Central Michigan University Y. S. Chen (陈永寿) China Institute of Atomic Energy

Contents l l l Introduction. Variation After 3 D Angular Momentum Projection. Examples of 26 Mg and 28 Si with the USD interaction. Systematic calculations for the sd and pf shell nuclei with the USD and GXPF 1 A interactions. PCI calculations for 52 Fe and 56 Ni. Summary.

Introduction Shell model Good: Ø Very successful in the description of various observables. Good shell model Hamiltonians. USD, GXPF 1 A, etc. Bad: Ø Ø Huge dimension. (Treatments: Mont Carlo shell Model, VAMPIR, etc) No intrinsic structure (deformation) 24 Mg and 26 Mg are triaxially deformed! [D. Kurath, Phys. Rev. C 5, 768 (1972)]

Mean Field (HF or HFB) Good: Ø Ø Bad: Ø Ø Very clear intrinsic structure. Applied to the whole nuclear region. No good angular momentum. Missing correlations beyond mean field.

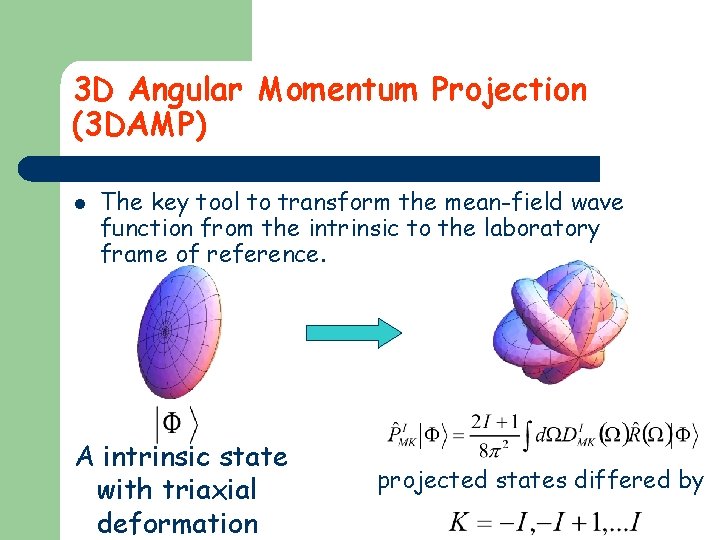
3 D Angular Momentum Projection (3 DAMP) l The key tool to transform the mean-field wave function from the intrinsic to the laboratory frame of reference. A intrinsic state with triaxial deformation projected states differed by

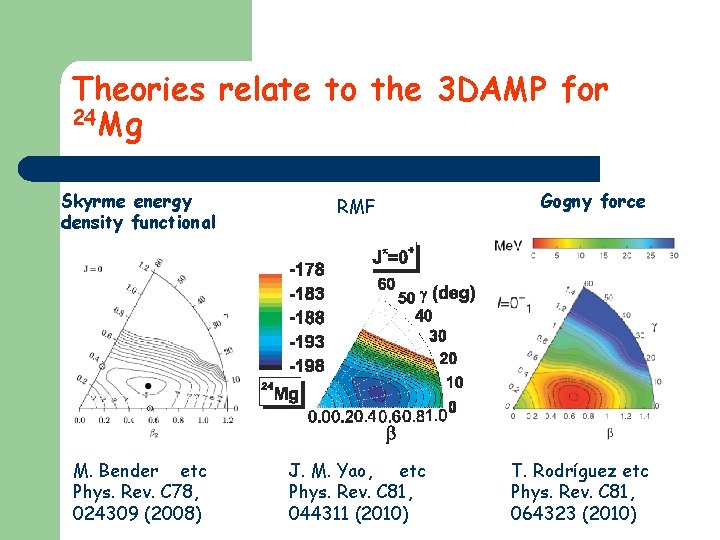
Theories relate to the 3 DAMP for 24 Mg Skyrme energy density functional RMF M. Bender etc Phys. Rev. C 78, 024309 (2008) J. M. Yao, etc Phys. Rev. C 81, 044311 (2010) Gogny force T. Rodríguez etc Phys. Rev. C 81, 064323 (2010)

What we are going to do : l l 1. 2. Obtaining shapes from well established shell model Hamiltonians. USD and GXPF 1 A Two ways: Hartree-Fock mean field Variation after Projection (VAP)

Variation After Projection : VAMPIR l l The only standard method where variation after angularmomentum projection is exactly considered (together with restoration of N, Z, and parity). Very complicated. Too much time consuming due to the five-fold integration. (3 for AMP and 2 for N, Z projection) No explicit discussions about the intrinsic triaxial shapes.

Present VAP is much simpler ! l Using HF type Slater determinant (HFB type in VAMPIR) Real HF transformation (Complex HFB in VAMPIR) Time reversal symmetry is imposed. l Gamma degree of freedom is allowed. l The adopted interactions: USD and GXPF 1 A l l

Basic idea of the present VAP HF type Slater determinant Wik are real here, determined by minimization of EPJ(I) Where f. K satisfy

Algorithm of the present VAP (L-BFGS quasi-Newton method) Thouless Theorem:

Problem: The VAP SD may have an arbitrary orientation in the space. Treatment: The 3 principle axes of the triaxial shape have to be in accord with the laboratory axes. Time reversal symmetry and Q 21=0

Quantities of Q and g for the deformed VAP Slater determinant

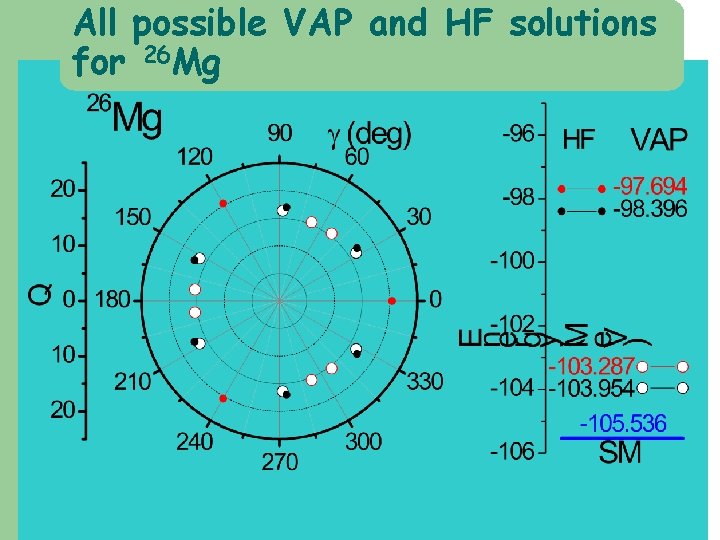
There may have several possible solutions in the VAP calculations. Needs to try many times to find out all minima. Ground state (I=0) of 26 Mg with USD interaction No EPJ(I=0) (Me. V) 1 -103. 954 2 -103. 954 3 -103. 954 4 -103. 954 5 -103. 954 6 -103. 954 7 -103. 287 8 -103. 954 9 -103. 954 10 -103. 287 Q 16. 372 15. 424 16. 372 15. 424 g 32. 017 -87. 982 87. 983 -152. 018 -32. 017 -52. 229 -32. 018 32. 017 -52. 229

All possible VAP and HF solutions for 26 Mg

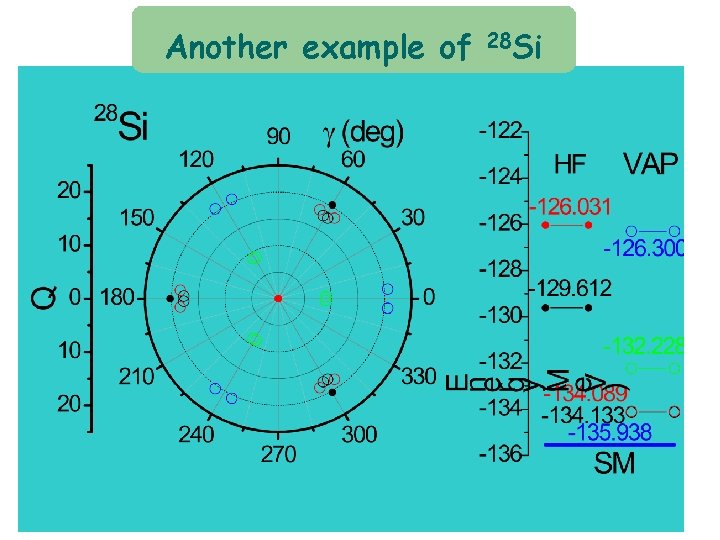
Another example of 28 Si

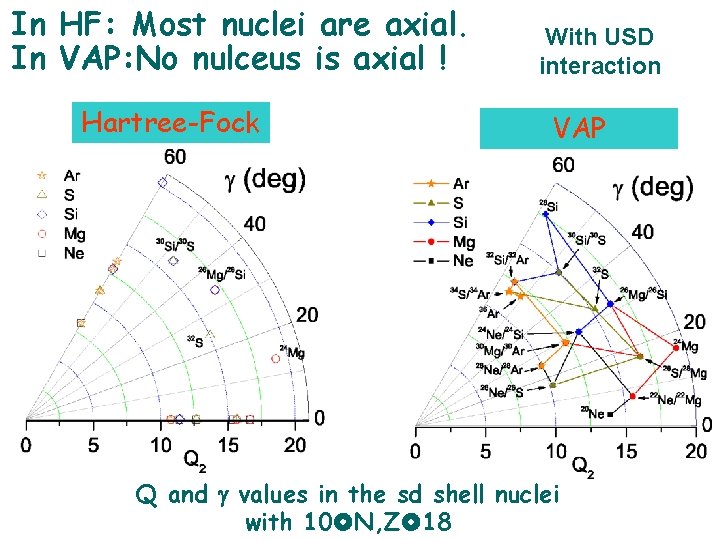
In HF: Most nuclei are axial. In VAP: No nulceus is axial ! Hartree-Fock With USD interaction VAP Q and g values in the sd shell nuclei with 10 N, Z 18

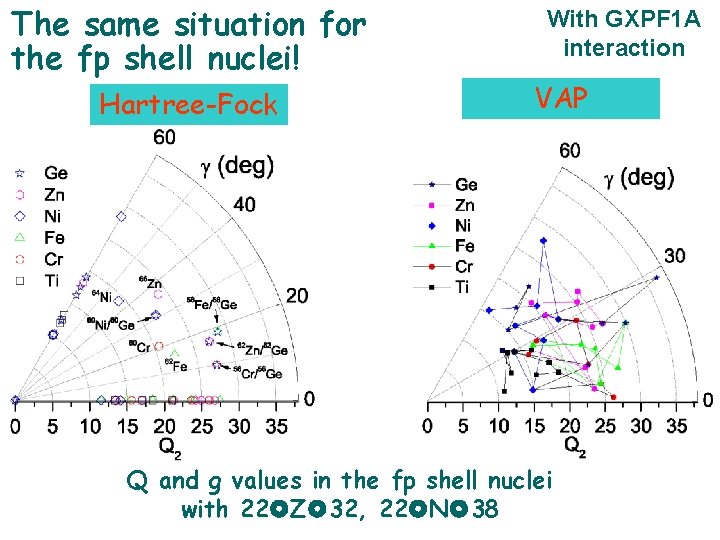
The same situation for the fp shell nuclei! Hartree-Fock With GXPF 1 A interaction VAP Q and g values in the fp shell nuclei with 22 Z 32, 22 N 38

Configuration interaction including Particle -Hole states (Triaxial Projected CI) Selection of the particle hole excited SDs (Gao, Horoi, PRC 79, 014311(2009) VAP SD Particle –Hole excitations on top of the VAP SD A Preliminary method!

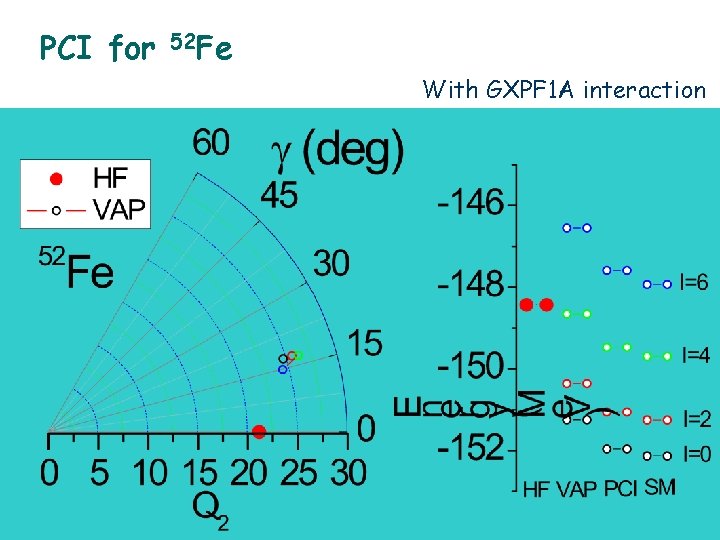
PCI for 52 Fe With GXPF 1 A interaction

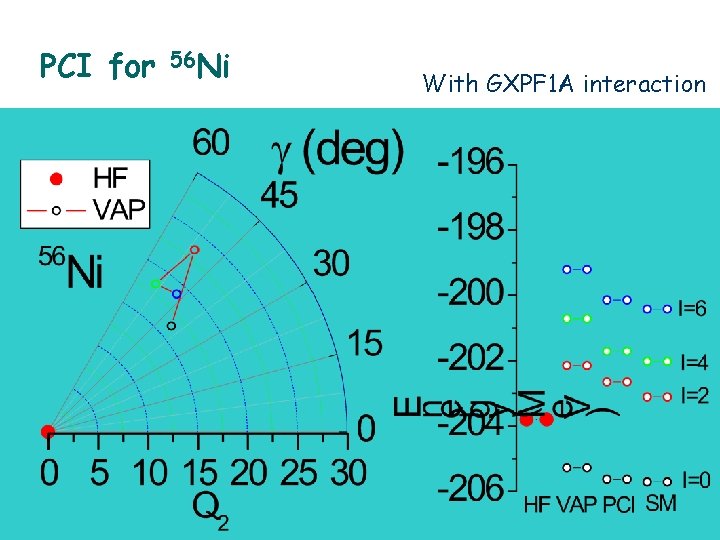
PCI for 56 Ni With GXPF 1 A interaction

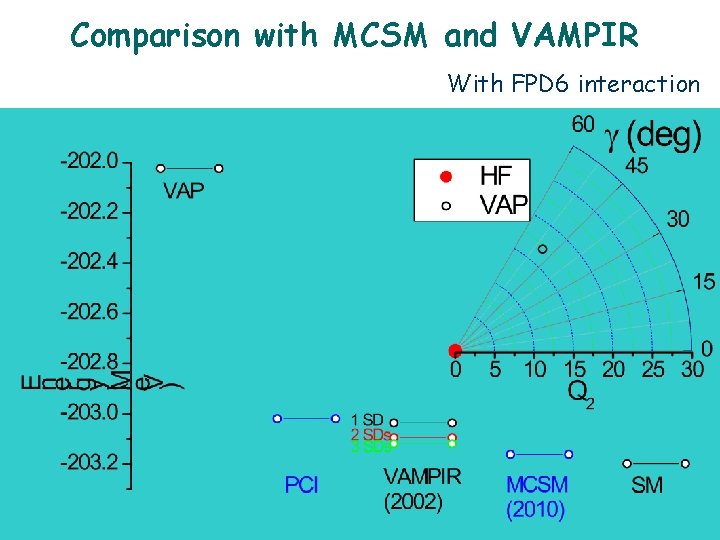
Comparison with MCSM and VAMPIR With FPD 6 interaction

Future work l VAP calculationd with unpaired SD for odd-spin states and odd mass nuclei (keeping the time reversal symmetry). l Non-axial octupole deformation will be included. l VAP for the excited states. l Try to improve the PCI algorithm.

Summary l l l Variation After Projection (VAP) calculations have been performed using Hartree-Fock type Slater determinant in the shell model space. Using USD and GXPF 1 A interaction, VAP calculations show that all the sd and fp shell nuclei are triaxial, while most nuclei are exactly axial in the HF calculations. Preliminary triaxial PCI calculations has been carried out and compared with the MSCM and VAMPIR.

Thanks for your attention!