TRIANGLES C N Coln Geometry St Barnabas H

TRIANGLES C. N. Colón Geometry St. Barnabas H. S. Bronx, NY

Classifying Triangles You will learn to identify the parts of triangles and to classify triangles by their parts. A polygon is a closed figure in a plane that is the union of line segments such that the line segments intersect only at their In geometry, a triangle is a polygon formed whenthree _____ noncollinear points endpoints and no segments sharing a common endpoint are connected by segments. collinear. D Each pair of segments forms an angle of the E triangle. Each angle is included between two lines. F The vertex of each angle is a vertex of the triangle. Each side is included between two vertices.

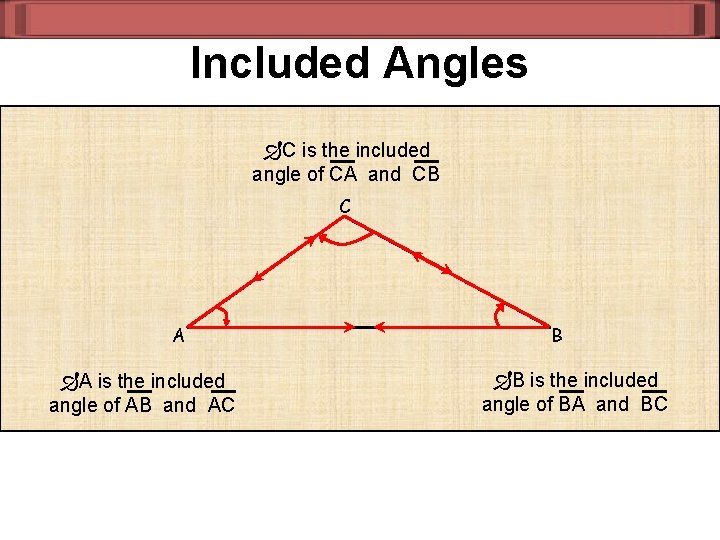
Included Angles C is the included angle of CA and CB C A A is the included angle of AB and AC B B is the included angle of BA and BC

Included Sides The side of a triangle that falls between two given angles is called the ______ included side of the angles. It is the one side common to both angles. C AC is the included side of A and C CB is the included side of C and B AB is the included side of A and B You can show that two triangles are congruent by using _____ two angles and the included side of the triangles. (This is the ASA Postulate…. LATER …. . LATER) ______

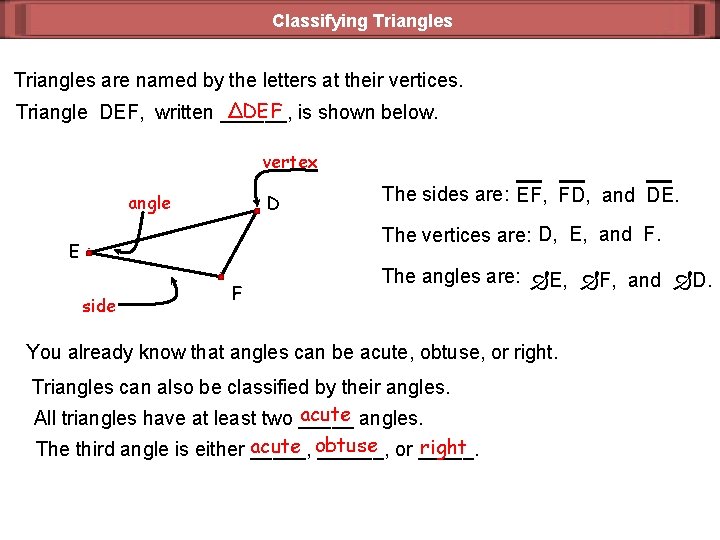
Classifying Triangles are named by the letters at their vertices. ΔDEF is shown below. Triangle DEF, written ______, vertex angle D The sides are: EF, FD, and DE. The vertices are: D, E, and F. E side F The angles are: E, F, and D. You already know that angles can be acute, obtuse, or right. Triangles can also be classified by their angles. acute angles. All triangles have at least two _____ right The third angle is either acute _____, obtuse ______, or _____.

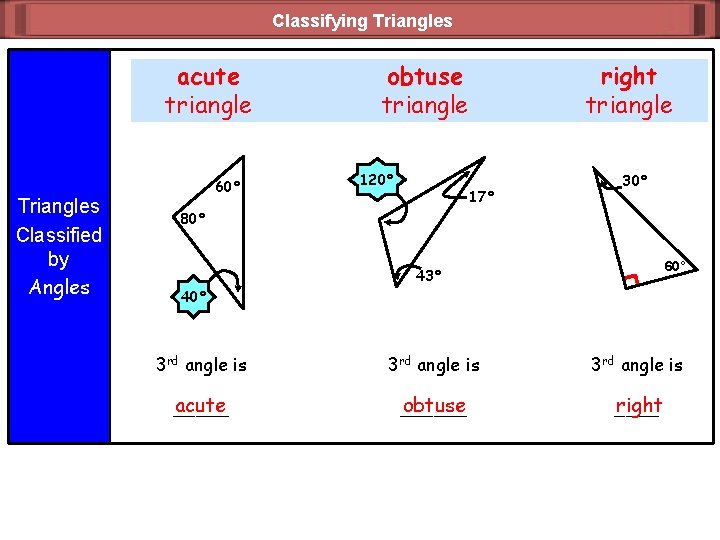
Classifying Triangles acute triangle Triangles Classified by Angles 60° obtuse triangle 120° right triangle 17° 30° 80° 60° 43° 40° 3 rd angle is acute _____ obtuse ______ right ____

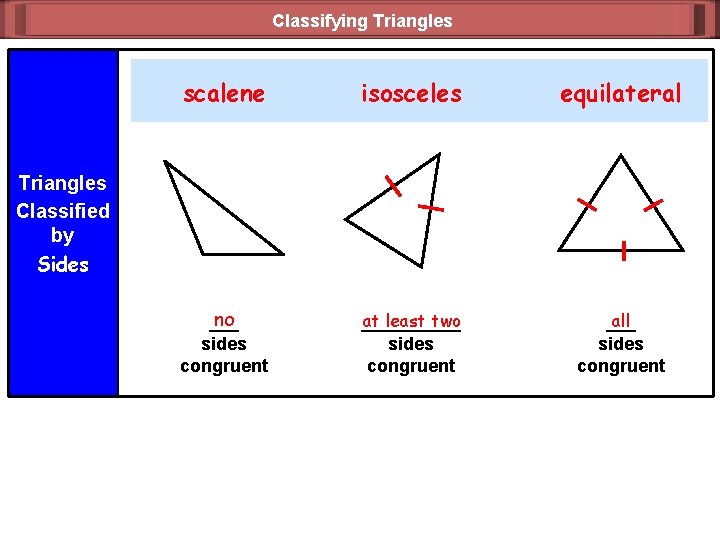
Classifying Triangles scalene isosceles equilateral no ___ sides congruent at least two _____ sides congruent all ___ sides congruent Triangles Classified by Sides

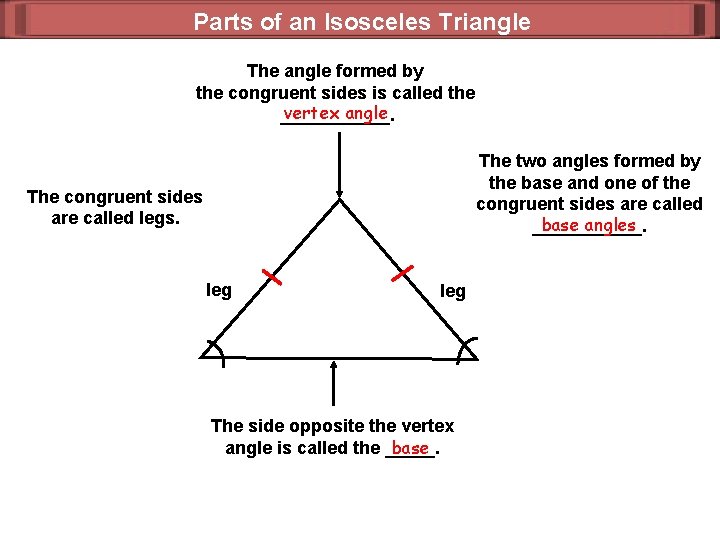
Parts of an Isosceles Triangle The angle formed by the congruent sides is called the vertex angle ______. The two angles formed by the base and one of the congruent sides are called base angles ______. The congruent sides are called legs. leg The side opposite the vertex angle is called the _____. base

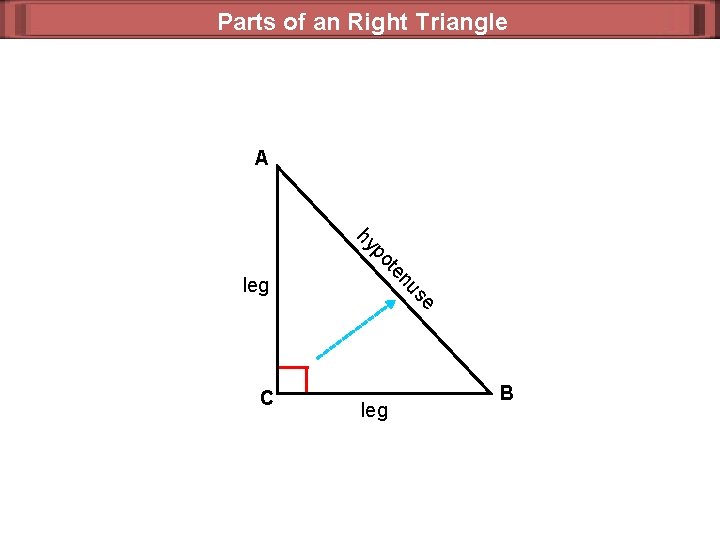
Parts of an Right Triangle A n te po hy e us leg C leg B

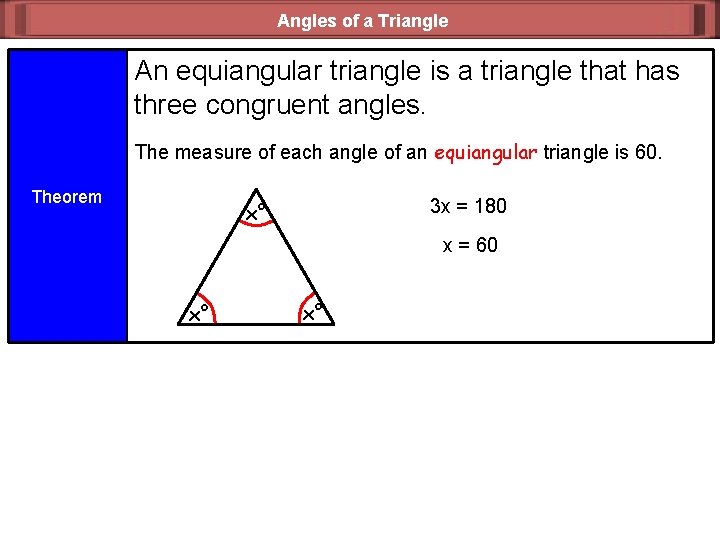
Angles of a Triangle An equiangular triangle is a triangle that has three congruent angles. The measure of each angle of an equiangular triangle is 60. Theorem 3 x = 180 x° x = 60 x° x°

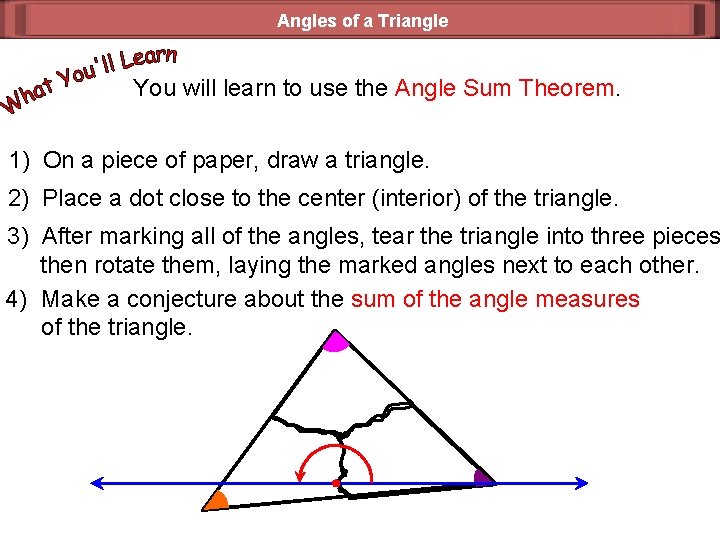
Angles of a Triangle You will learn to use the Angle Sum Theorem. 1) On a piece of paper, draw a triangle. 2) Place a dot close to the center (interior) of the triangle. 3) After marking all of the angles, tear the triangle into three pieces then rotate them, laying the marked angles next to each other. 4) Make a conjecture about the sum of the angle measures of the triangle.

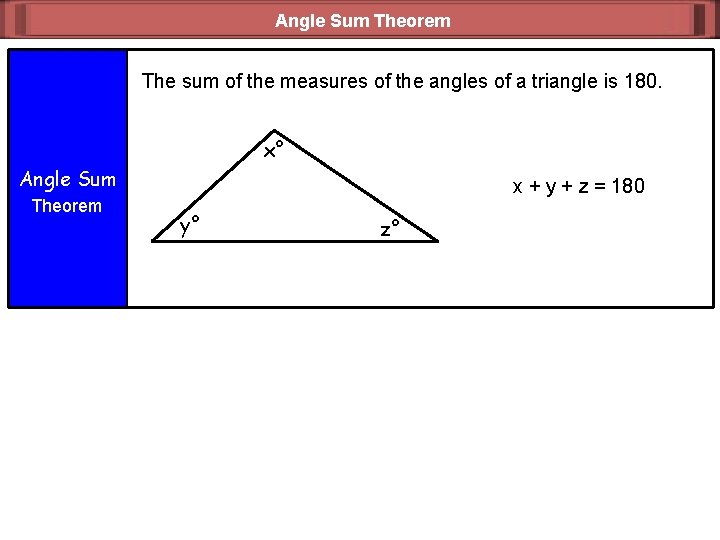
Angle Sum Theorem The sum of the measures of the angles of a triangle is 180. x° Angle Sum Theorem x + y + z = 180 y° z°

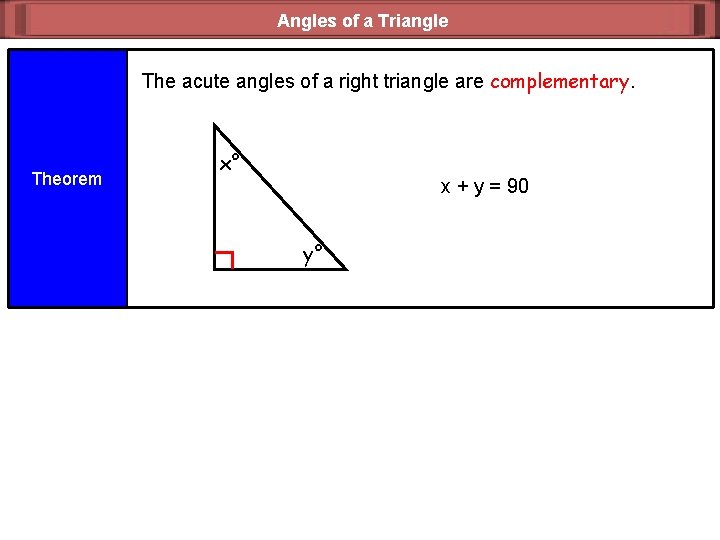
Angles of a Triangle The acute angles of a right triangle are complementary. Theorem x° x + y = 90 y°

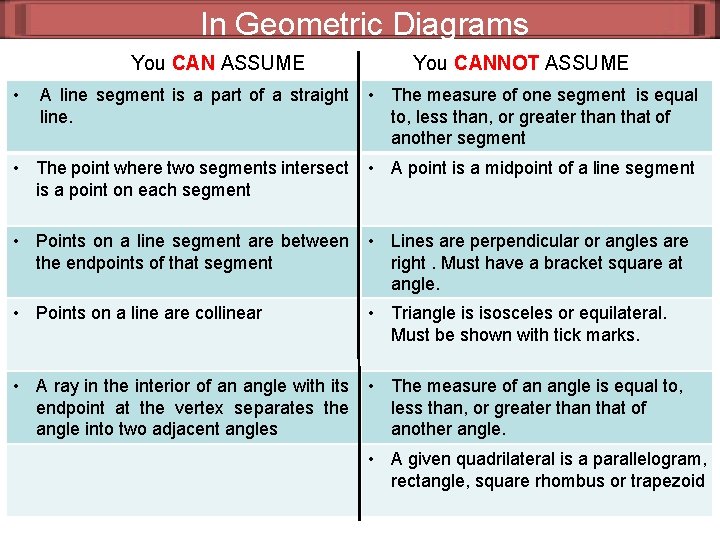
In Geometric Diagrams You CAN ASSUME • You CANNOT ASSUME A line segment is a part of a straight line. • The measure of one segment is equal to, less than, or greater than that of another segment • The point where two segments intersect is a point on each segment • A point is a midpoint of a line segment • Points on a line segment are between the endpoints of that segment • Lines are perpendicular or angles are right. Must have a bracket square at angle. • Points on a line are collinear • Triangle is isosceles or equilateral. Must be shown with tick marks. • A ray in the interior of an angle with its endpoint at the vertex separates the angle into two adjacent angles • The measure of an angle is equal to, less than, or greater than that of another angle. • A given quadrilateral is a parallelogram, rectangle, square rhombus or trapezoid

ASSIGNMENT p. 27 #4 -18 (e) p. 31 Chapter Review #1 -22 (all)