Triangle Scan Conversion Rasterization Rasterization scan conversion Determine

Triangle Scan Conversion

Rasterization • Rasterization (scan conversion) – Determine which pixels that are inside primitive specified by a set of vertices – Produces a set of fragments – Fragments have a location (pixel location) and other attributes such color and texture coordinates that are determined by interpolating values at vertices • Pixel colors determined later using color, texture, and other vertex properties 2 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

Triangle Area Filling Algorithms • Why do we care about triangles? • Edge Equations • Edge Walking

Do something easier! • Instead of polygons, let’s do something easy! • TRIANGLES! Why? 1) All polygons can be broken into triangles 2) Easy to specify 3) Always convex 4) Going to 3 D is MUCH easier

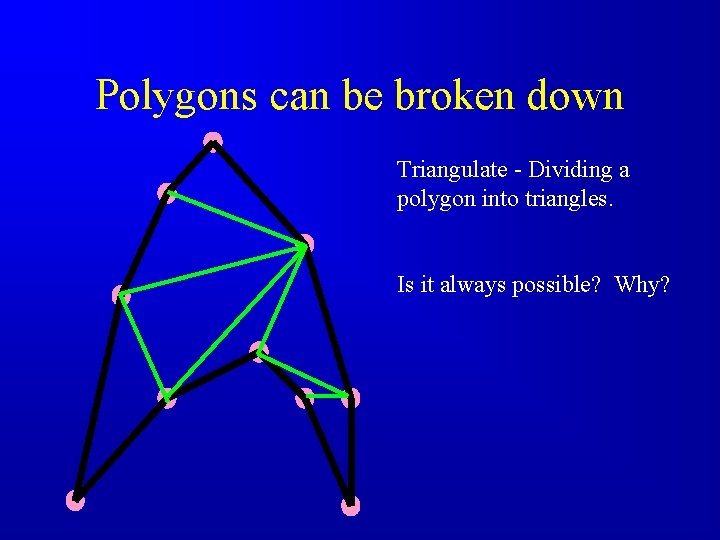
Polygons can be broken down Triangulate - Dividing a polygon into triangles. Is it always possible? Why?

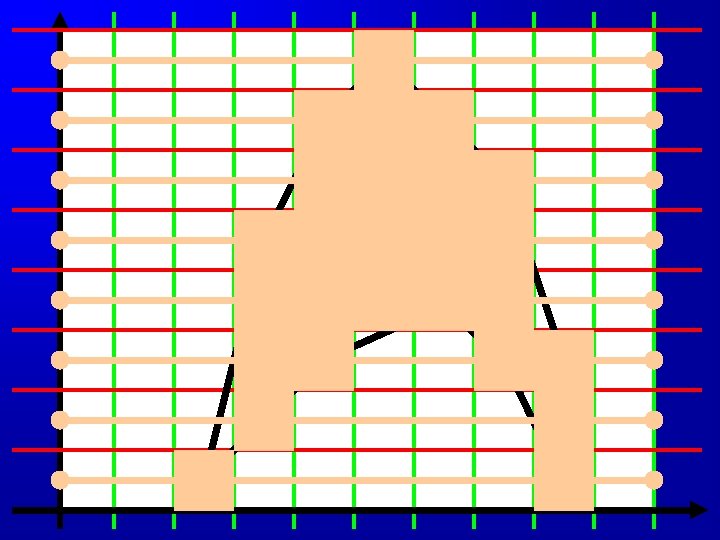
Any object can be broken down into polygons

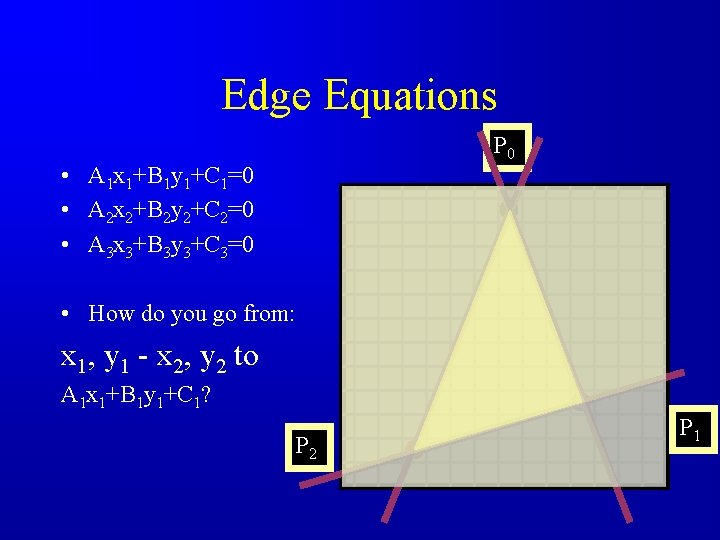
Specifying a model • For polygons, we had to worry about connectivity AND vertices. • How would you specify a triangle? (What is the minimum you need to draw one? ) – Only vertices (x 1, y 1) (x 2, y 2) (x 3, y 3) – No ambiguity – Line equations A 1 x 1+B 1 y 1+C 1=0 A 2 x 2+B 2 y 2+C 2=0 A 3 x 3+B 3 y 3+C 3=0

Triangles are always convex • What is a convex shape? An object is convex if and only if any line segment connecting two points on its boundary is contained entirely within the object or one of its boundaries. Think about scan lines again!

Scan Converting a Triangle • Recap what we are trying to do • Two main ways to rasterize a triangle – Edge Equations • A 1 x 1+B 1 y 1+C 1=0 • A 2 x 2+B 2 y 2+C 2=0 • A 3 x 3+B 3 y 3+C 3=0 – Edge Walking

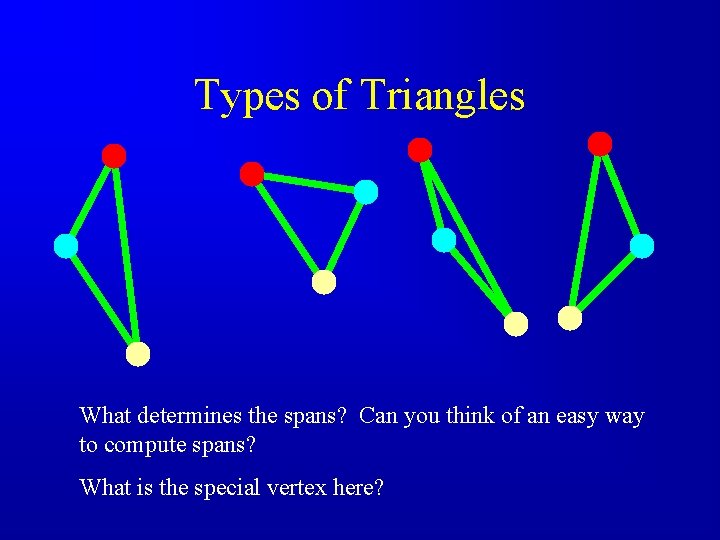
Types of Triangles What determines the spans? Can you think of an easy way to compute spans? What is the special vertex here?

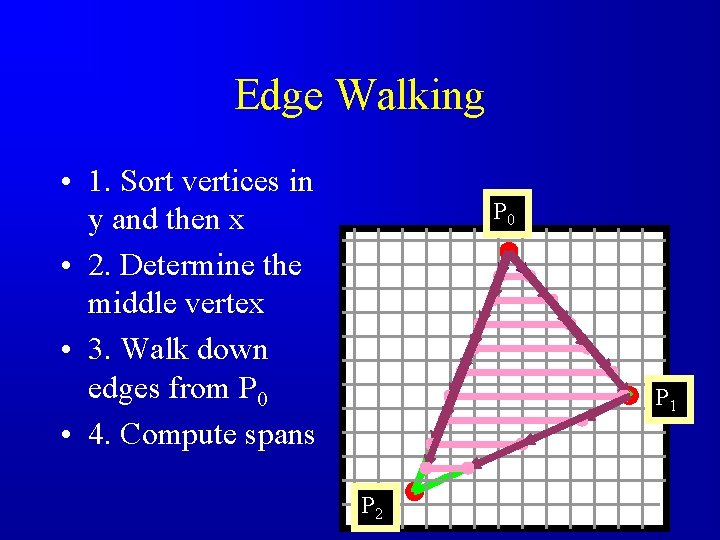
Edge Walking • 1. Sort vertices in y and then x • 2. Determine the middle vertex • 3. Walk down edges from P 0 • 4. Compute spans P 0 P 1 P 2

Edge Walking Pros and Cons Pros • Fast • Easy to implement in hardware Cons • Special Cases • Interpolation can be tricky

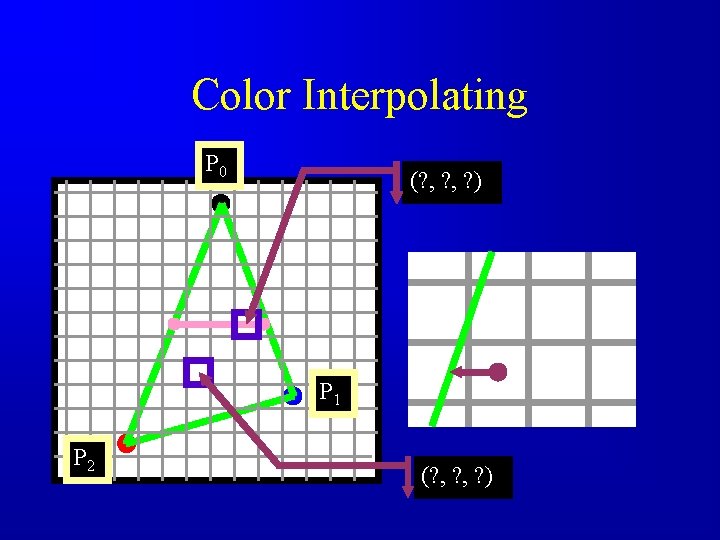
Color Interpolating P 0 (? , ? ) P 1 P 2 (? , ? )

Edge Equations P 0 • A 1 x 1+B 1 y 1+C 1=0 • A 2 x 2+B 2 y 2+C 2=0 • A 3 x 3+B 3 y 3+C 3=0 • How do you go from: x 1, y 1 - x 2, y 2 to A 1 x 1+B 1 y 1+C 1? P 2 P 1

Given 2 points, compute A, B, C C = x 0 y 1 – x 1 y 0 A = y 0 – y 1 B = x 1 – x 0

Edge Equations P 0 • What does the edge equation mean? • A 1 x 1+B 1 y 1+C 1=0 • Pt 1[2, 1], Pt 2[6, 11] • A=-10, B=4, C=16 • What is the value of the equation for the: – gray part – yellow part – the boundary line • What happens when we reverse P 0 and P 1? P 1

Combining all edge equations P 0 1) Determine edge equations for all three edges 2) Find out if we should reverse the edges 3) Create a bounding box 4) Test all pixels in the bounding box whether they too reside on the same side P 1 P 2

Edge Equations: Interpolating Color • Given redness at the 3 vertices, set up the linear system of equations: • The solution works out to:

Edge Equations: Interpolating Color • Notice that the columns in the matrix are exactly the coefficients of the edge equations! • So the setup cost per parameter is basically a matrix multiply • Per-pixel cost (the inner loop) cost equates to tracking another edge equation value (which is? ) – A: 1 add

Pros and Cons of Edge Equations • Pros • Cons • If you have the right • Can be expensive if hardware (Pixel. Planes) you don’t have then it is very fast hardware • Fast tests • 50% efficient • Easy to interpolate colors

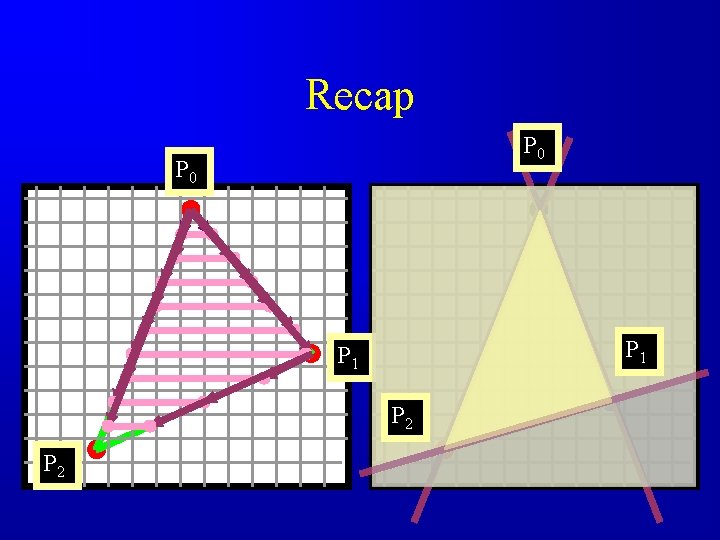
Recap P 0 P 1 P 2

Scan Conversion of Line Segments • Start with line segment in window coordinates with integer values for endpoints • Assume implementation has a write_pixel function y = mx + h 23 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

DDA Algorithm • Digital Differential Analyzer – DDA was a mechanical device for numerical solution of differential equations – Line y=mx+ h satisfies differential equation where m = Dy/Dx = y 2 -y 1/x 2 -x 1 • Along scan line Dx = 1 at each iteration of the loop For(x=x 1; x<=x 2, ix++) { y+=m; write_pixel(x, round(y), line_color) } 24 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

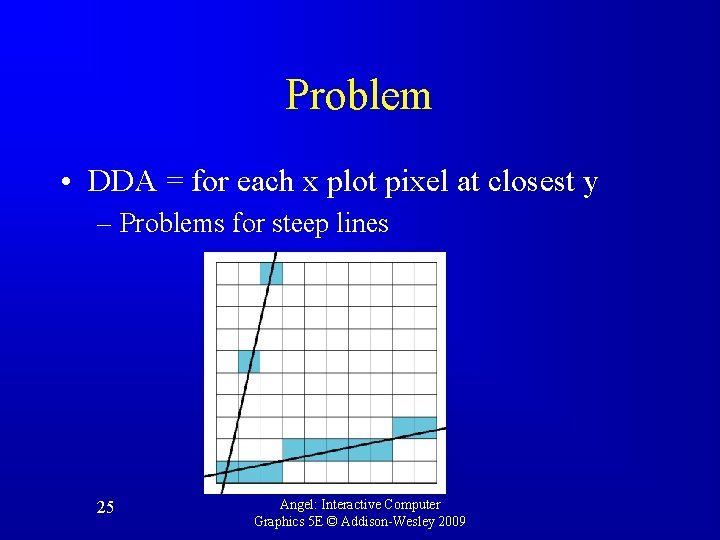
Problem • DDA = for each x plot pixel at closest y – Problems for steep lines 25 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

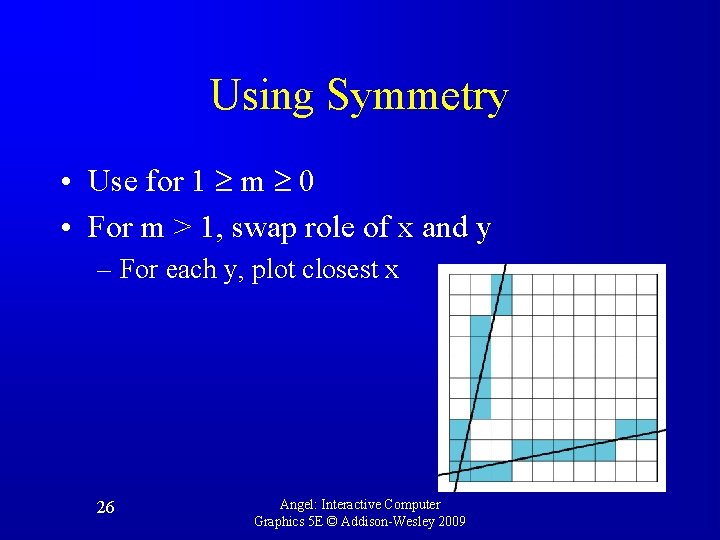
Using Symmetry • Use for 1 m 0 • For m > 1, swap role of x and y – For each y, plot closest x 26 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

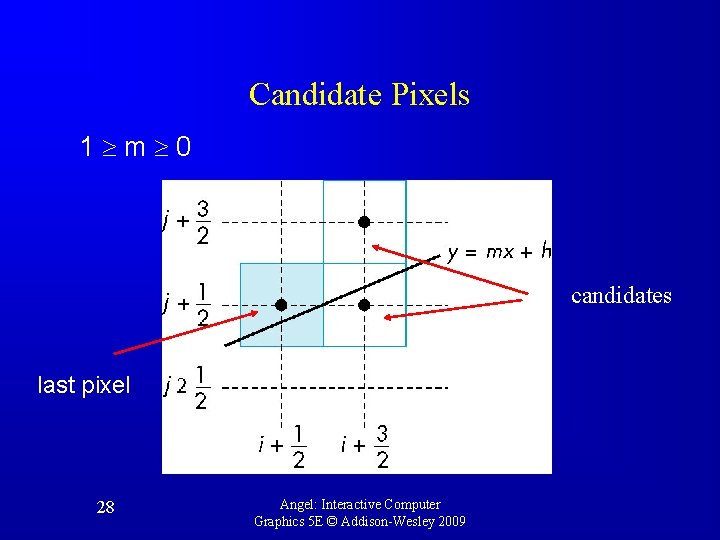
Bresenham’s Algorithm • DDA requires one floating point addition per step • We can eliminate all fp through Bresenham’s algorithm • Consider only 1 m 0 – Other cases by symmetry • Assume pixel centers are at half integers • If we start at a pixel that has been written, there are only two candidates for the next pixel to be written into the frame buffer 27 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

Candidate Pixels 1 m 0 candidates last pixel 28 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

Decision Variable d = Dx(b-a) d is an integer d > 0 use upper pixel d < 0 use lower pixel 29 - Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

Incremental Form • More efficient if we look at dk, the value of the decision variable at x = k dk+1= dk – 2 Dy, if dk <0 dk+1= dk – 2(Dy- Dx), otherwise • For each x, we need do only an integer addition and a test • Single instruction on graphics chips 30 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009