Triangle Proportionality Theorem Objectives Students will learn to

Triangle Proportionality Theorem Objectives Students will learn to how to apply Triangle Proportionality theorem to find segment lengths.

Triangle Proportionality Theorem

Triangle Proportionality Theorem Example 1: Finding the Length of a Segment Find US. It is given that , so by the Triangle Proportionality Theorem. Substitute 14 for RU, 4 for VT, and 10 for RV. US(10) = 56 Cross Products Prop. Divide both sides by 10.

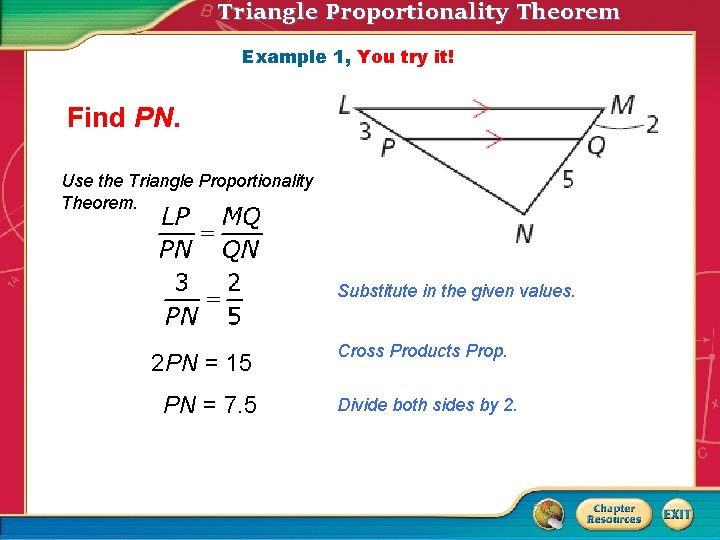
Triangle Proportionality Theorem Example 1, You try it! Find PN. Use the Triangle Proportionality Theorem. Substitute in the given values. 2 PN = 15 PN = 7. 5 Cross Products Prop. Divide both sides by 2.

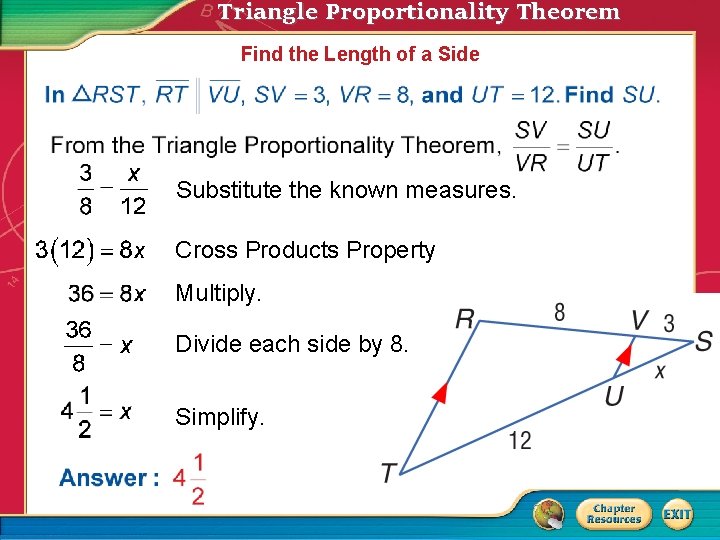
Triangle Proportionality Theorem Find the Length of a Side Substitute the known measures. Cross Products Property Multiply. Divide each side by 8. Simplify.

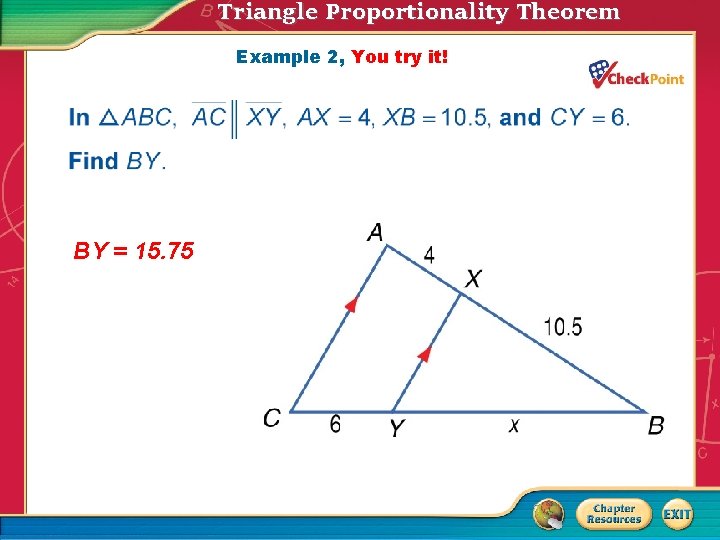
Triangle Proportionality Theorem Example 2, You try it! BY = 15. 75

Triangle Proportionality Theorem Example 3: Verifying Segments are Parallel Verify that Since . , by the Converse of the Triangle Proportionality Theorem.

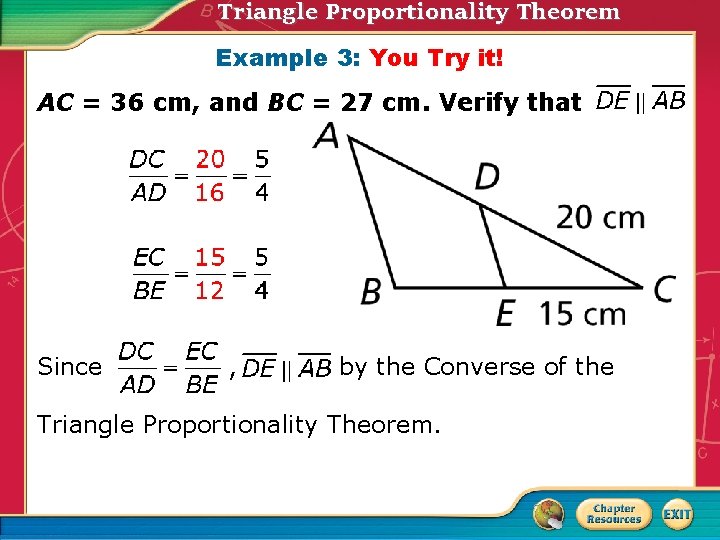
Triangle Proportionality Theorem Example 3: You Try it! AC = 36 cm, and BC = 27 cm. Verify that Since , by the Converse of the Triangle Proportionality Theorem. .

Triangle Proportionality Theorem Determine if Lines are Parallel In order to show that we must show that Since the sides are proportional. Answer: Since the segments have proportional lengths, GH || FE.

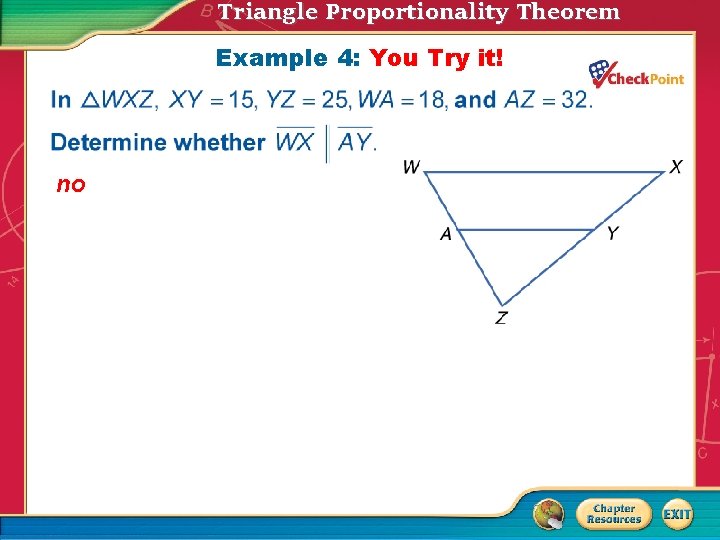
Triangle Proportionality Theorem Example 4: You Try it! no

Triangle Proportionality Theorem

Triangle Proportionality Theorem Example 5: Art Application Suppose that an artist decided to make a larger sketch of the trees. In the figure, if AB = 4. 5 in. , BC = 2. 6 in. , CD = 4. 1 in. , and KL = 4. 9 in. , find LM and MN to the nearest tenth of an inch. Given 2 -Trans. Proportionality Corollary Sub. 4. 9 for KL, 4. 5 for AB, and 2. 6 for BC. 4. 5(LM) = 4. 9(2. 6) Cross Products Prop. LM 2. 8 in. Divide both sides by 4. 5.

Triangle Proportionality Theorem Example 5: Art Application Continued… 2 -Trans. Proportionality Corollary Substitute 4. 9 for KL, 4. 5 for AB, and 4. 1 for CD. 4. 5(MN) = 4. 9(4. 1) Cross Products Prop. MN 4. 5 in. Divide both sides by 4. 5.

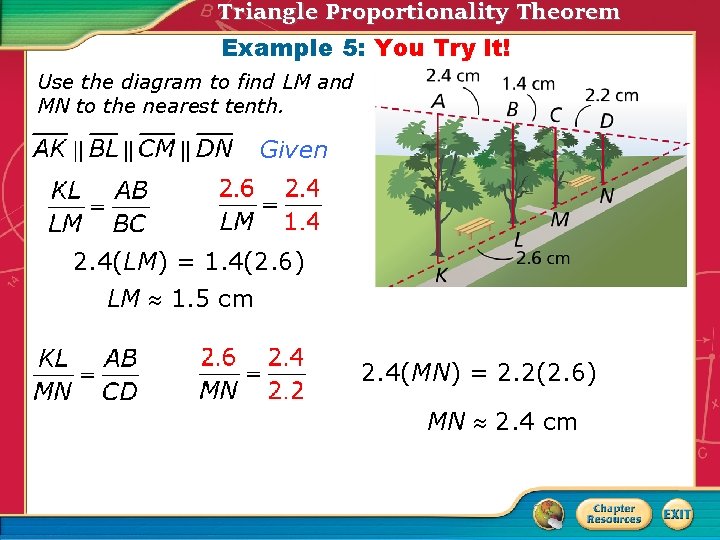
Triangle Proportionality Theorem Example 5: You Try It! Use the diagram to find LM and MN to the nearest tenth. Given 2. 4(LM) = 1. 4(2. 6) LM 1. 5 cm 2. 4(MN) = 2. 2(2. 6) MN 2. 4 cm

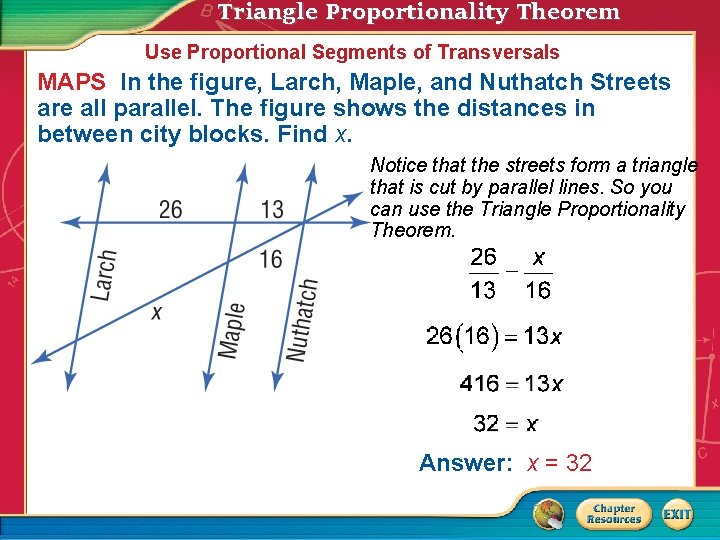
Triangle Proportionality Theorem Use Proportional Segments of Transversals MAPS In the figure, Larch, Maple, and Nuthatch Streets are all parallel. The figure shows the distances in between city blocks. Find x. Notice that the streets form a triangle that is cut by parallel lines. So you can use the Triangle Proportionality Theorem. Answer: x = 32

Triangle Proportionality Theorem Example 6: You Try It! In the figure, Davis, Broad, and Main Streets are all parallel. The figure shows the distances in between city blocks. Find x. X=5

Triangle Proportionality Theorem The previous theorems and corollary lead to the following conclusion.

Triangle Proportionality Theorem Example 6: Using the Triangle Angle Bisector Theorem Find PS and SR. by the ∆ Bisector Theorem. 40(x – 2) = 32(x + 5) 40 x – 80 = 32 x + 160 8 x = 240 x = 30 Substitute 30 for x. PS = x – 2 = 30 – 2 = 28 SR = x + 5 = 30 + 5 = 35

Triangle Proportionality Theorem Example 6: You Try It! Find AC and DC. by the ∆ Bisector Theorem. 4 y = 4. 5 y – 9 – 0. 5 y = – 9 y = 18 So DC = 9 and AC = 16.

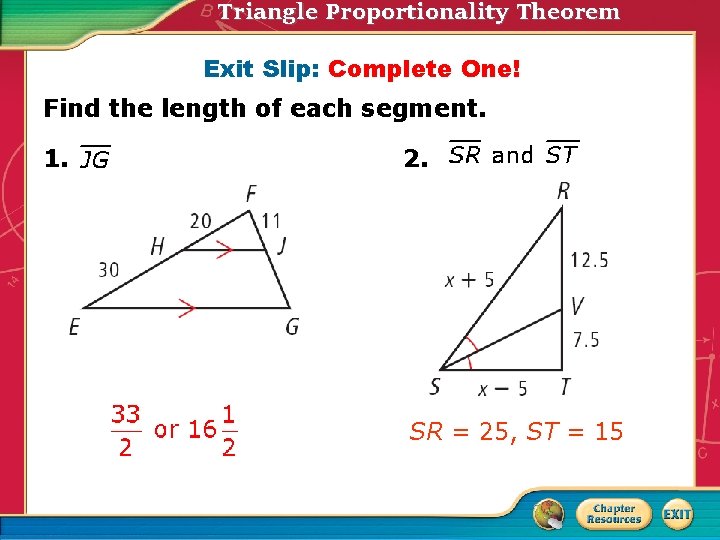
Triangle Proportionality Theorem Exit Slip: Complete One! Find the length of each segment. 1. 2. SR = 25, ST = 15