Triangle Nonlocality Genuine quantum triangle nonlocality and Finner

Triangle Nonlocality Genuine quantum triangle nonlocality and Finner inequality Marc-Olivier Renou, Yuyi Wang, Sadra Boreiri, Salman Beigi, Nicolas Gisin, and Nicolas Brunner, ar. Xiv: 1901. 08287, PRL 123, 070403 (2019) Marc-Olivier Renou, Elisa Bäumer, Sadra Boreiri, Nicolas Brunner, Nicolas Gisin, and Salman Beigi, ar. Xiv: 1905. 04902, PRL 123, 140401 (2019) QIP 2020 Shenzhen

Triangle Nonlocality Genuine quantum triangle nonlocality and Finner inequality I. Introduction: the triangle scenario II. A genuine quantum nonlocal distribution III. The Finner inequality

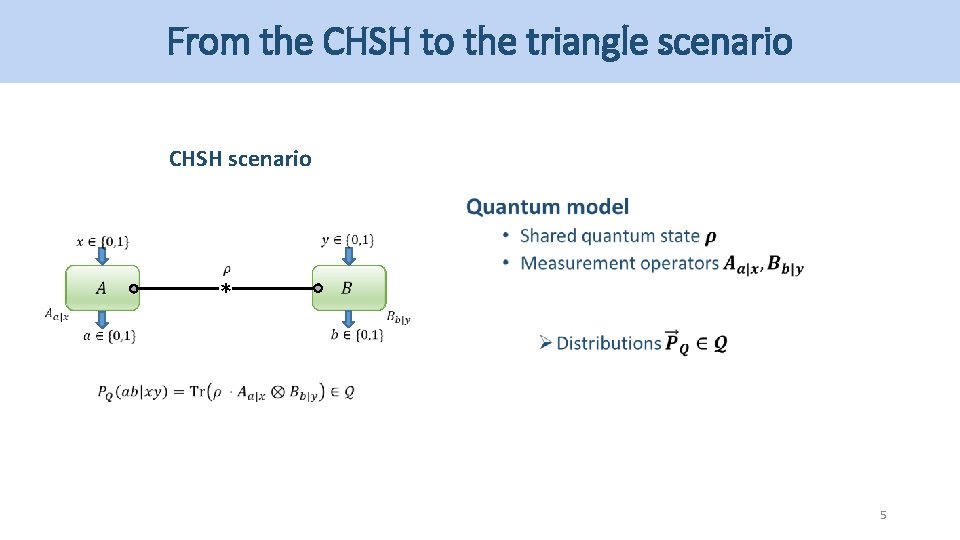
From the CHSH to the triangle scenario CHSH scenario * * 3

From the CHSH to the triangle scenario CHSH scenario * 4

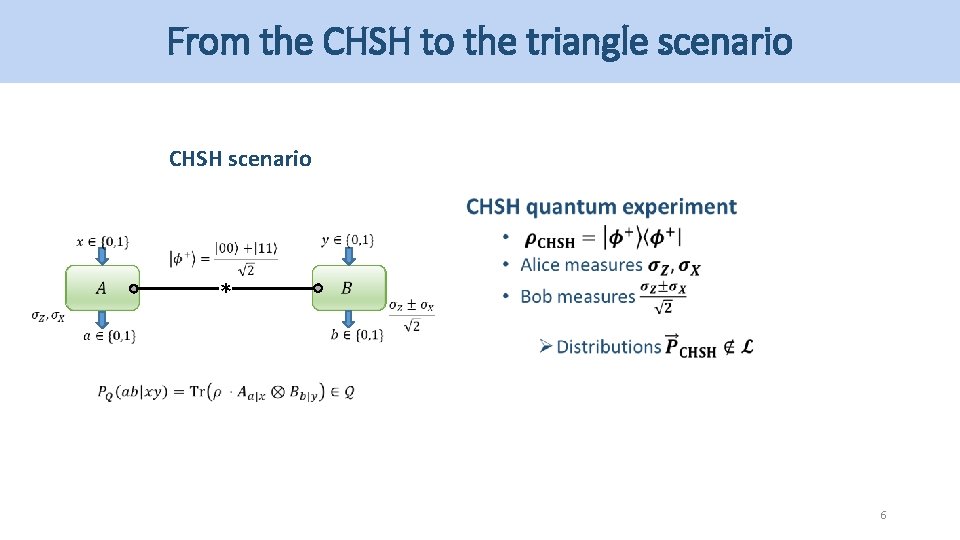
From the CHSH to the triangle scenario CHSH scenario * 5

From the CHSH to the triangle scenario CHSH scenario * 6

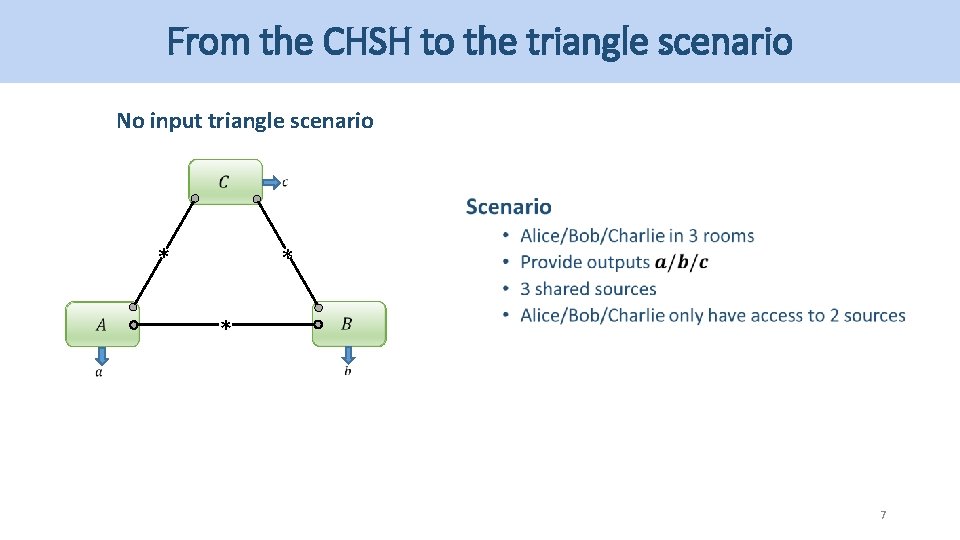
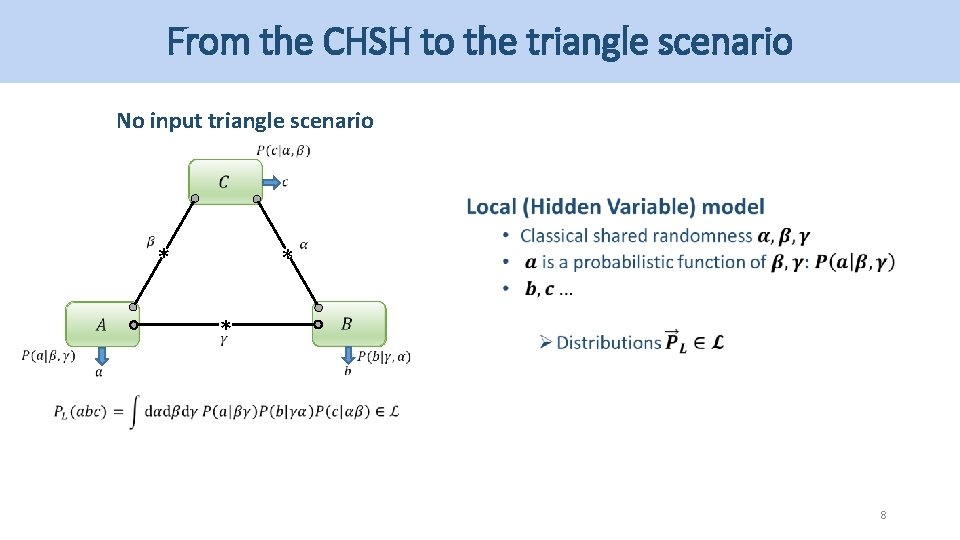
From the CHSH to the triangle scenario No input triangle scenario * * * 7

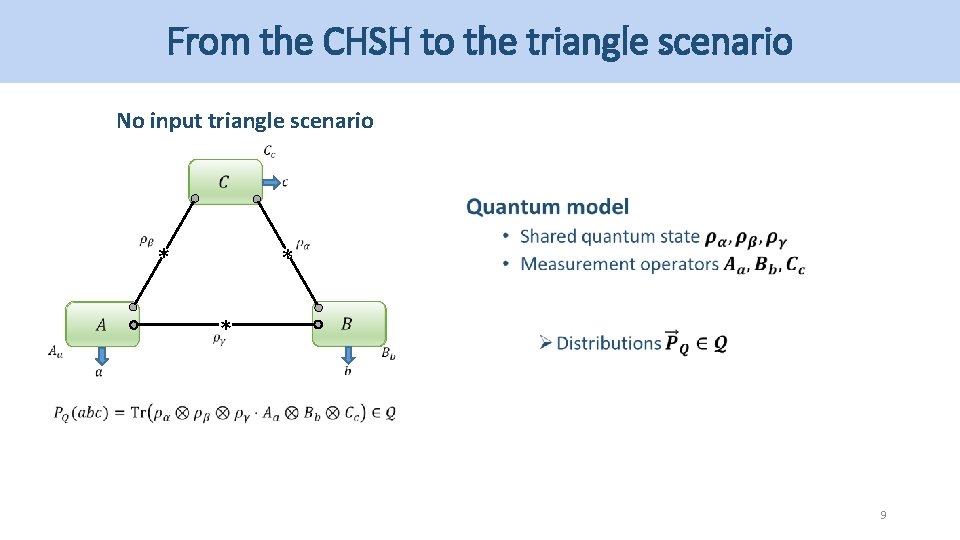
From the CHSH to the triangle scenario No input triangle scenario * * * 8

From the CHSH to the triangle scenario No input triangle scenario * * * 9

From the CHSH to the triangle scenario No input triangle scenario * * * ? Difficult question… 10

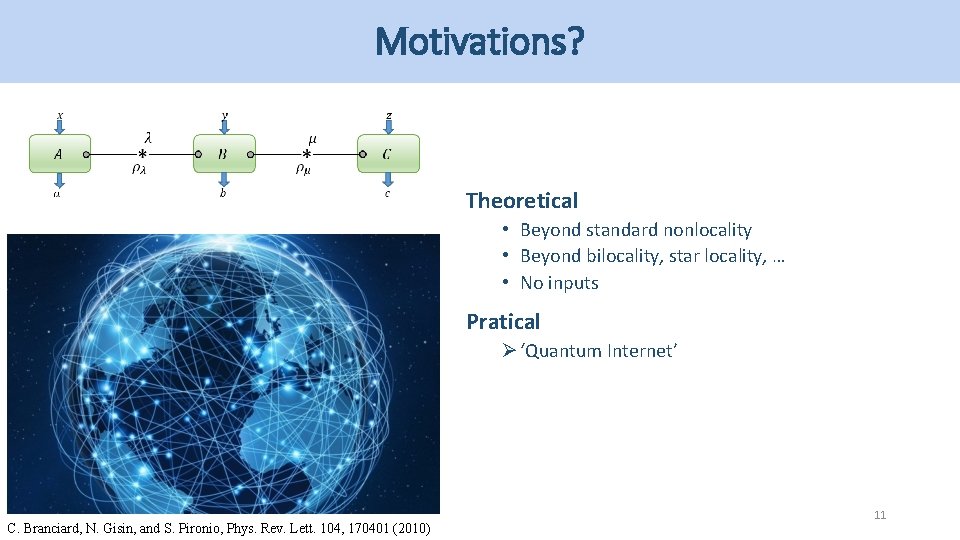
Motivations? Theoretical • Beyond standard nonlocality • Beyond bilocality, star locality, … • No inputs Pratical Ø ‘Quantum Internet’ C. Branciard, N. Gisin, and S. Pironio, Phys. Rev. Lett. 104, 170401 (2010) 11

Triangle Nonlocality Genuine quantum triangle nonlocality and Finner inequality I. Introduction: the triangle scenario II. A genuine quantum nonlocal distribution III. The Finner inequality

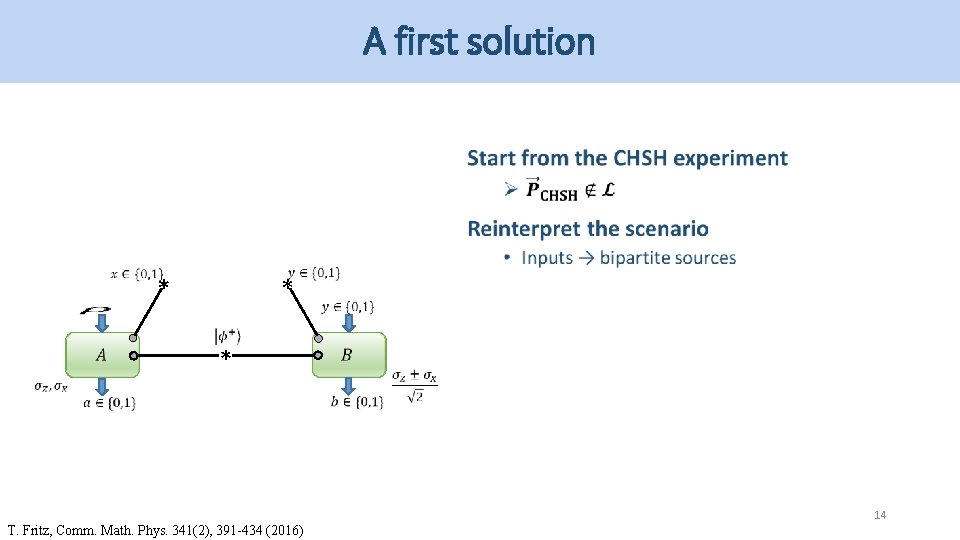
A first solution * 13 T. Fritz, Comm. Math. Phys. 341(2), 391 -434 (2016)

A first solution * * * 14 T. Fritz, Comm. Math. Phys. 341(2), 391 -434 (2016)

A first solution * * 15 T. Fritz, Comm. Math. Phys. 341(2), 391 -434 (2016)

A first solution Too simple? Limitations * * • Only one quantum state • No entangled measurement • Reinterpretation of standard CHSH scenario * 16 T. Fritz, Comm. Math. Phys. 341(2), 391 -434 (2016)

The ‘triangle problem’ * * Another solution? * 17

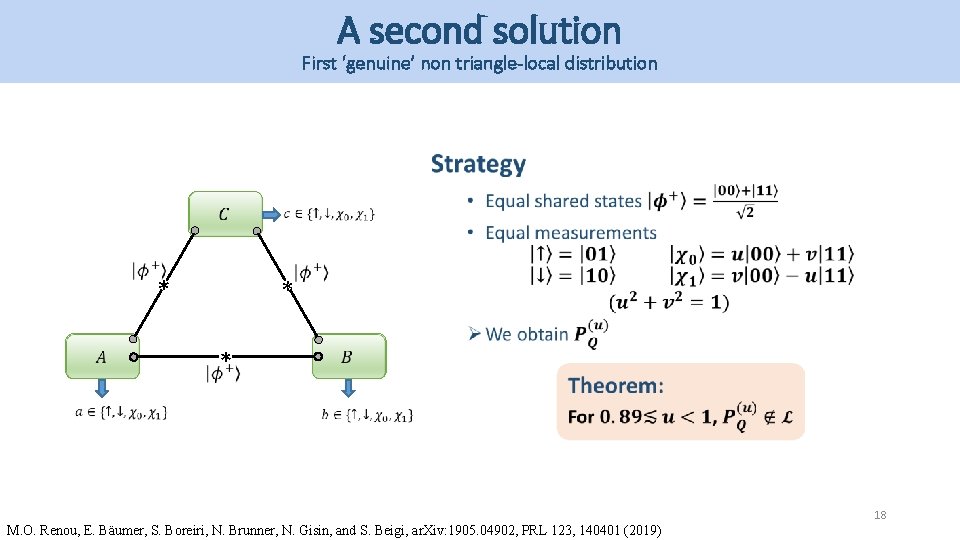
A second solution First ‘genuine’ non triangle-local distribution * * * 18 M. O. Renou, E. Bäumer, S. Boreiri, N. Brunner, N. Gisin, and S. Beigi, ar. Xiv: 1905. 04902, PRL 123, 140401 (2019)

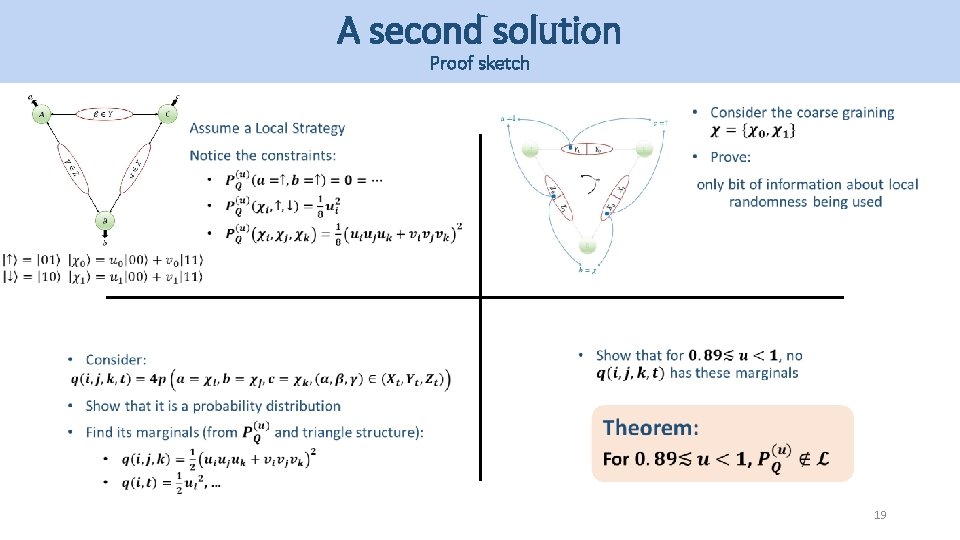
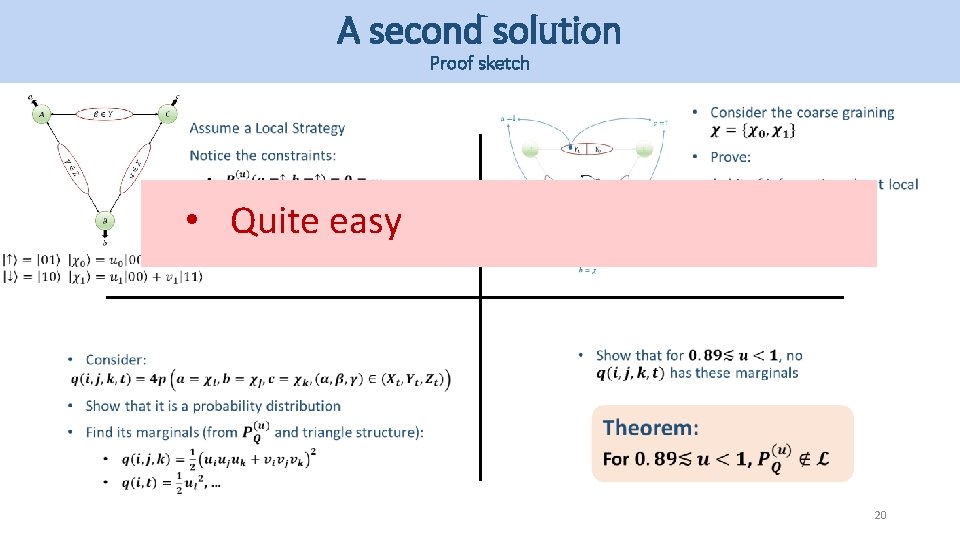
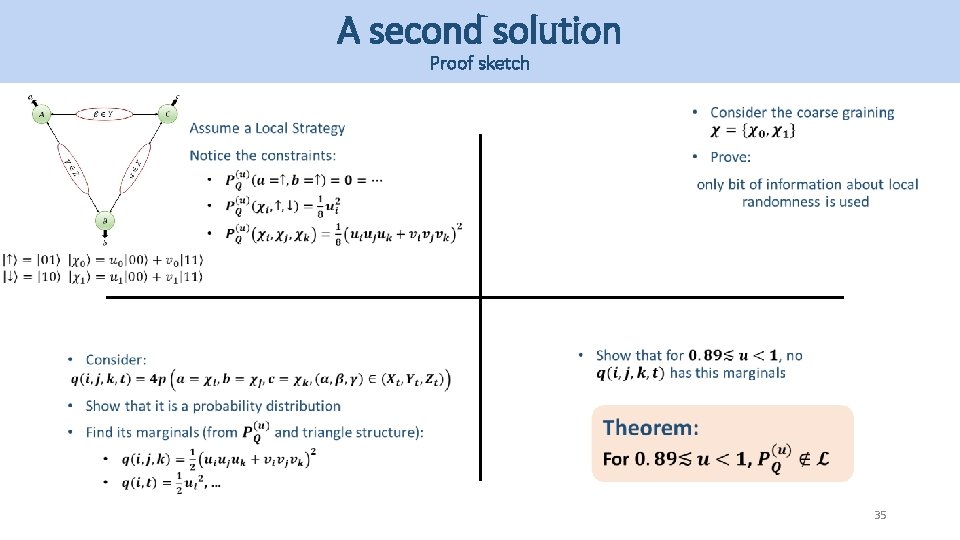
A second solution Proof sketch 19

A second solution Proof sketch • Quite easy 20

A second solution Proof sketch 21

A second solution Proof sketch 22

A second solution First ‘genuine’ non triangle-local distribution Improvements • All three sources are entangled • Relies on entangled joint measurement * * * Questions • Need entangled states / measurements? • Noise tolerance? • Experiment? 23 M. O. Renou, E. Bäumer, S. Boreiri, N. Brunner, N. Gisin, and S. Beigi, ar. Xiv: 1905. 04902, PRL 123, 140401 (2019)

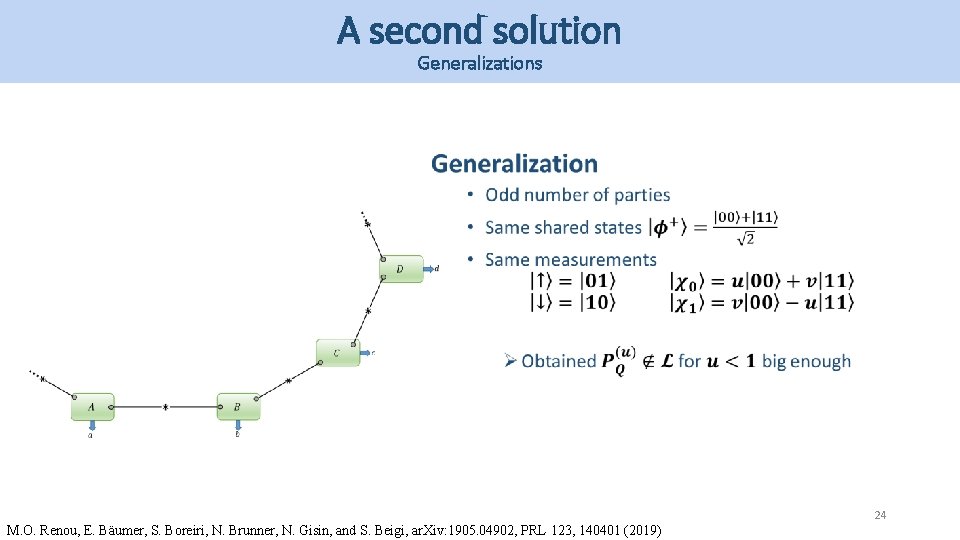
A second solution Generalizations 24 M. O. Renou, E. Bäumer, S. Boreiri, N. Brunner, N. Gisin, and S. Beigi, ar. Xiv: 1905. 04902, PRL 123, 140401 (2019)

Triangle Nonlocality Genuine quantum triangle nonlocality and Finner inequality I. Introduction: the triangle scenario II. A genuine quantum non local distribution III. The Finner inequality

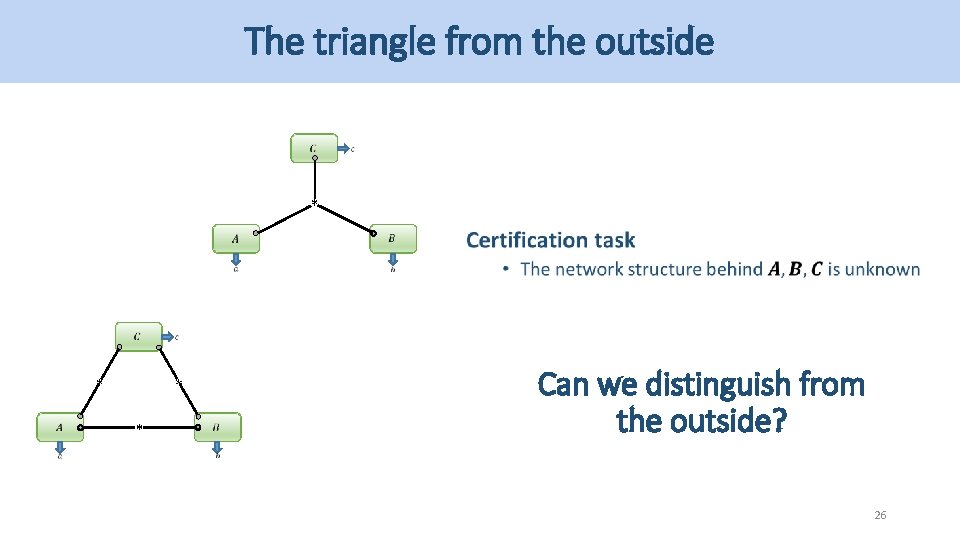
The triangle from the outside * * Can we distinguish from the outside? 26

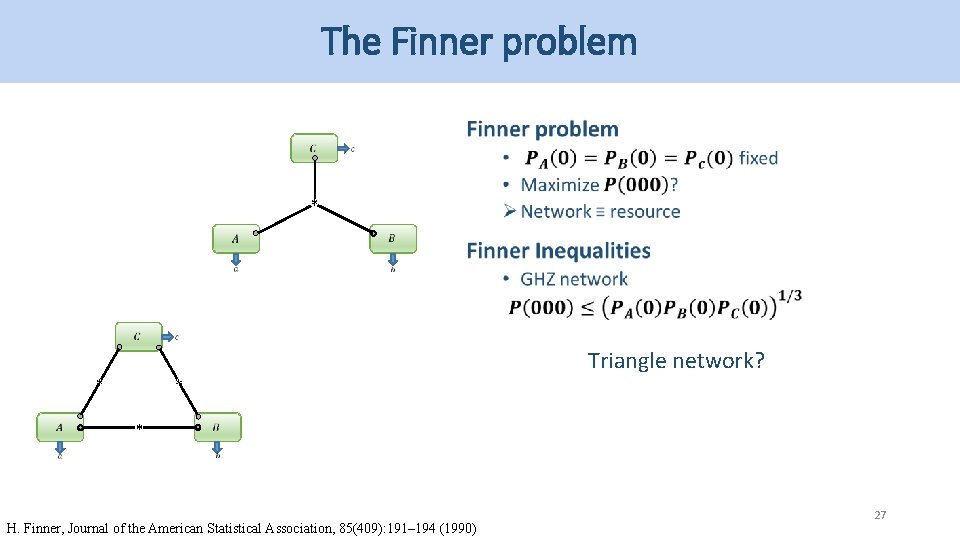
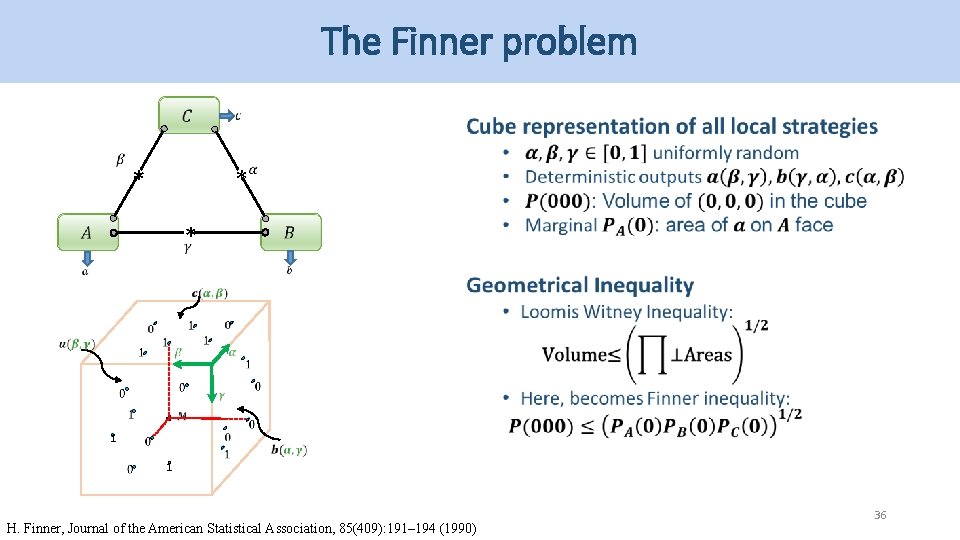
The Finner problem * * Triangle network? * * H. Finner, Journal of the American Statistical Association, 85(409): 191– 194 (1990) 27

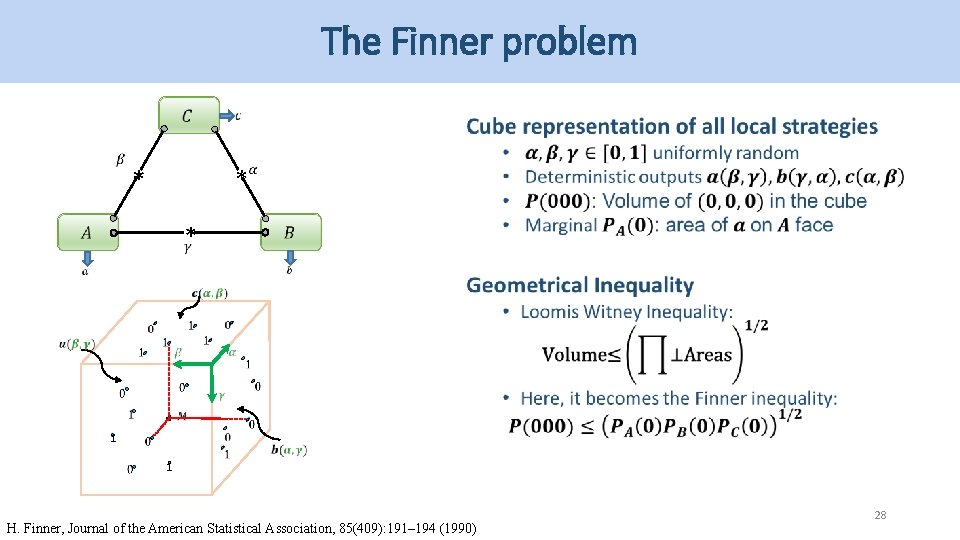
The Finner problem * * * 1 1 H. Finner, Journal of the American Statistical Association, 85(409): 191– 194 (1990) 28

The Finner problem * * * 1 1 H. Finner, Journal of the American Statistical Association, 85(409): 191– 194 (1990) 29

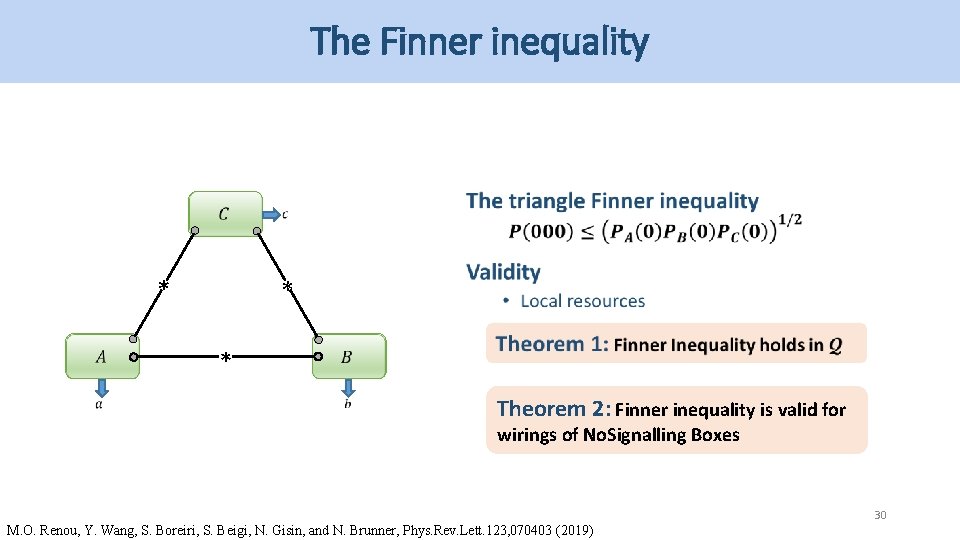
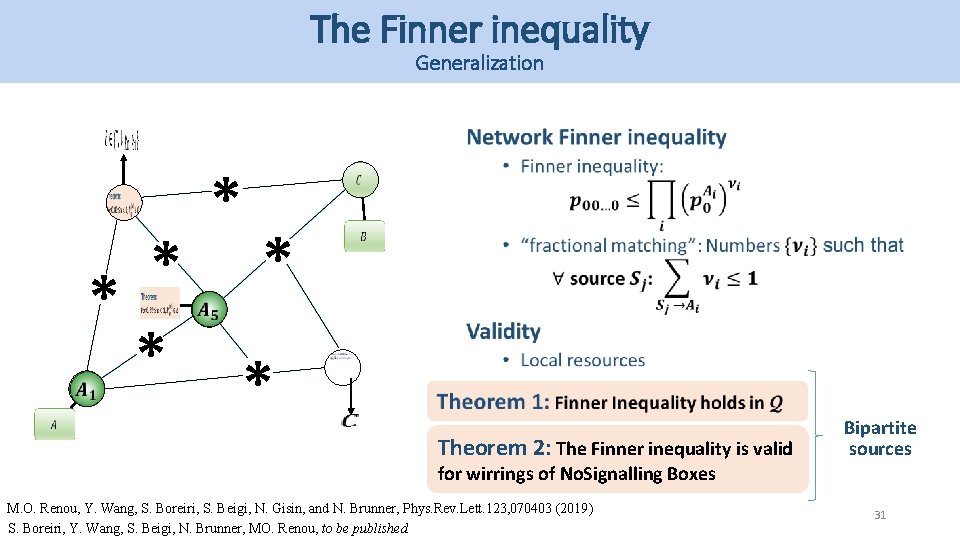
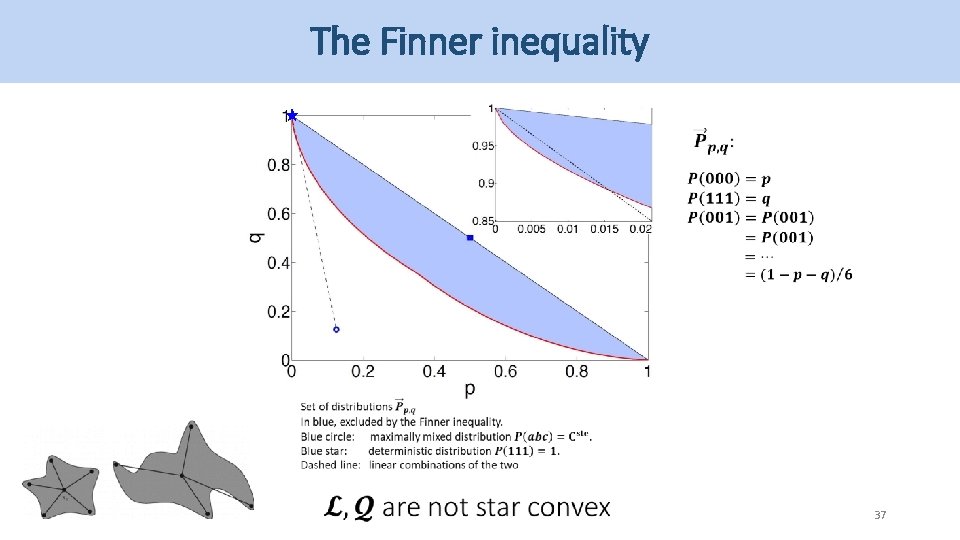
The Finner inequality * * * Theorem 2: Finner inequality is valid for wirings of No. Signalling Boxes 30 M. O. Renou, Y. Wang, S. Boreiri, S. Beigi, N. Gisin, and N. Brunner, Phys. Rev. Lett. 123, 070403 (2019)

The Finner inequality Generalization * * * Theorem 2: The Finner inequality is valid Bipartite sources for wirrings of No. Signalling Boxes M. O. Renou, Y. Wang, S. Boreiri, S. Beigi, N. Gisin, and N. Brunner, Phys. Rev. Lett. 123, 070403 (2019) S. Boreiri, Y. Wang, S. Beigi, N. Brunner, MO. Renou, to be published 31

Beyond the Finner problem The ‘reverse Finner problem’ * * K. He, L. Li, X. Liu, Y. Wang, and M. Xia, FOCS, 451– 462 (2017) 32

Acknowledgments

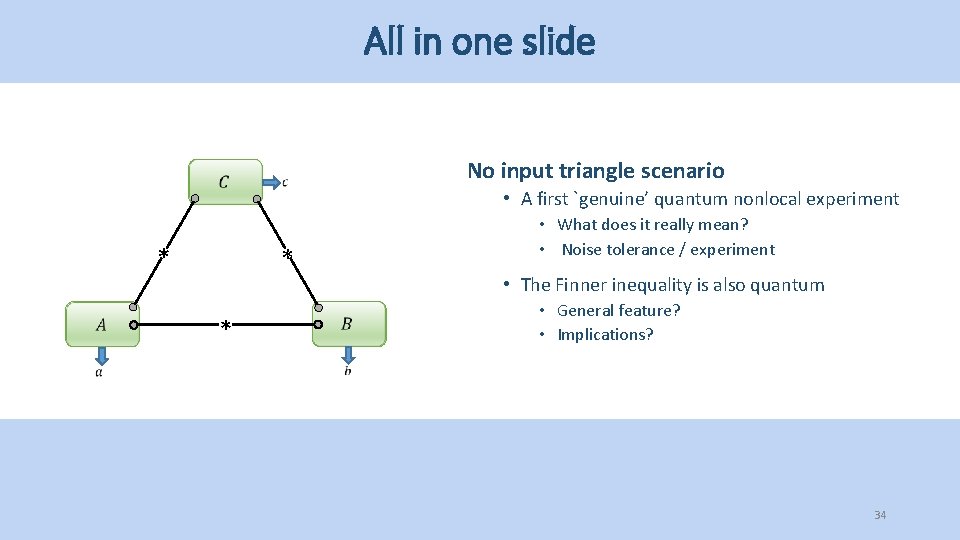
All in one slide No input triangle scenario • A first `genuine’ quantum nonlocal experiment * * • What does it really mean? • Noise tolerance / experiment • The Finner inequality is also quantum * • General feature? • Implications? 34

A second solution Proof sketch 35

The Finner problem * * * 1 1 H. Finner, Journal of the American Statistical Association, 85(409): 191– 194 (1990) 36

The Finner inequality 37