Triangle Midsegment Theorem Lesson 55 Saxon Geometry Essential









- Slides: 18

Triangle Midsegment Theorem Lesson 55 Saxon Geometry

Essential Questions 1. What is a midsegment of a triangle? 2. Which of the side lengths of a triangle is the midsegment’s length half of? 3. Which of the side lengths of a triangle is the midsegment parallel to? 4. How is a midsegment triangle related to the original triangle?

New Concepts: Lesson 55 • A midsegment of a triangle is a segment that joins the midpoints of two sides of the triangle. Every triangle has three midsegments. The midsegment is always half the length of the side that does not have a midsegment endpoint on it.

Triangle Midsegment Theorem

Using the Triangle Midsegment Theorem •

Using the Triangle Midsegment Theorem •

Theorem 55 -2

Using Theorem 55 -2 • In the diagram, what are the values of a and b?

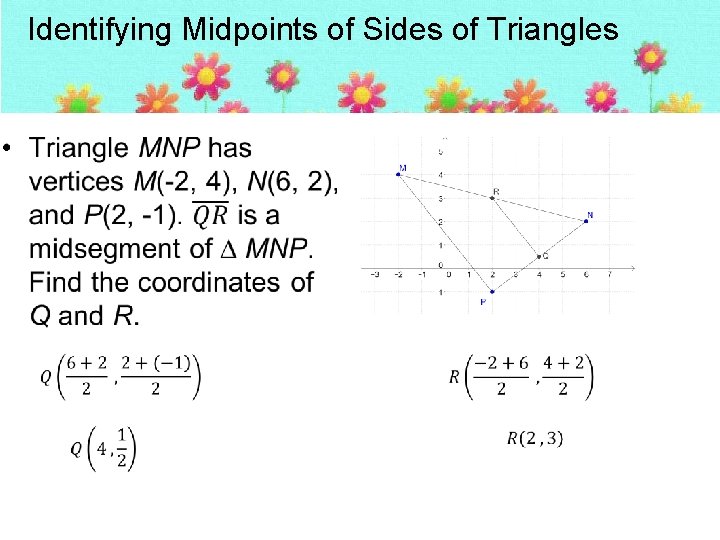
Identifying Midpoints of Sides of Triangles •

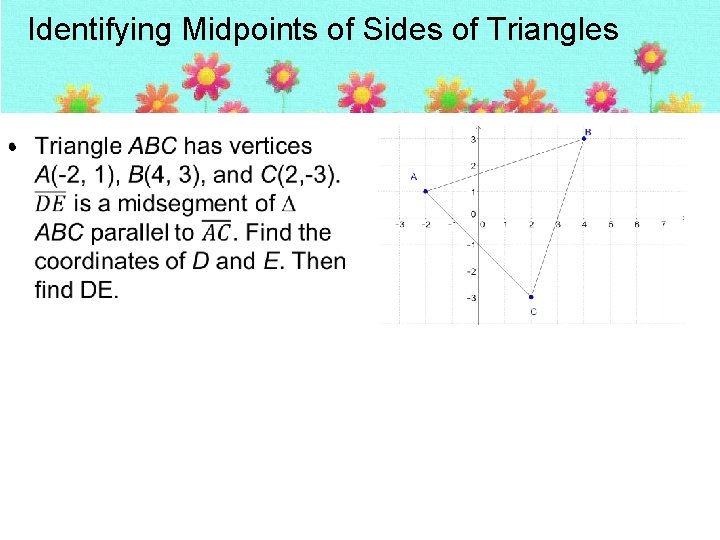
Identifying Midpoints of Sides of Triangles •

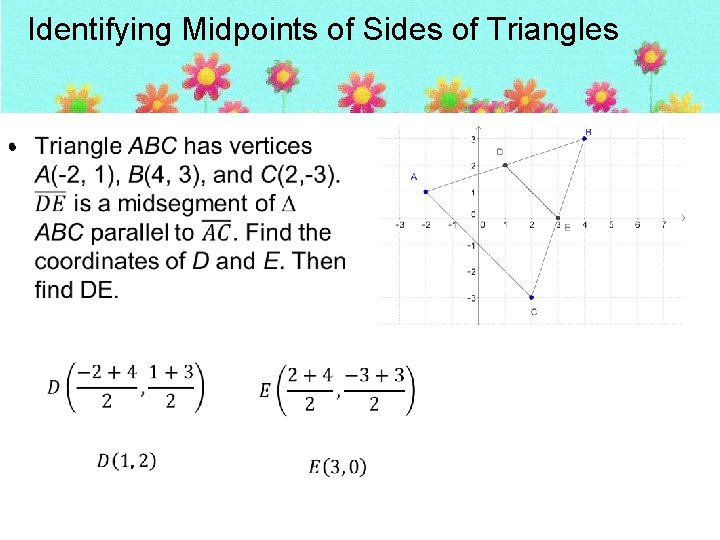
Identifying Midpoints of Sides of Triangles •

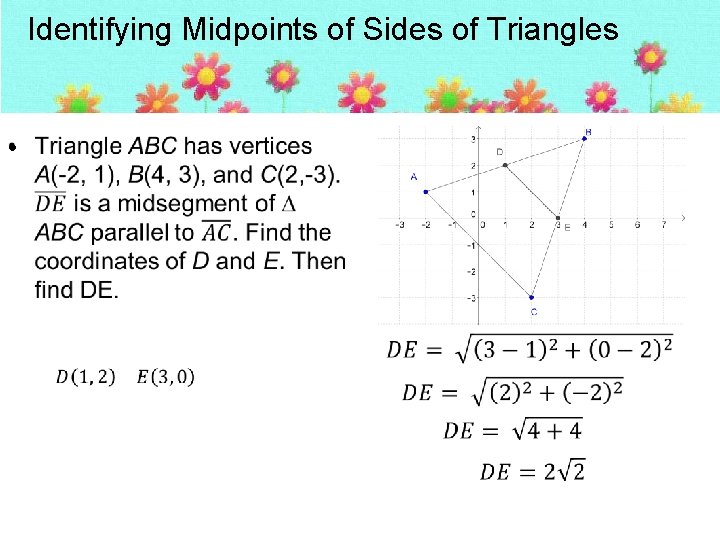
Identifying Midpoints of Sides of Triangles •

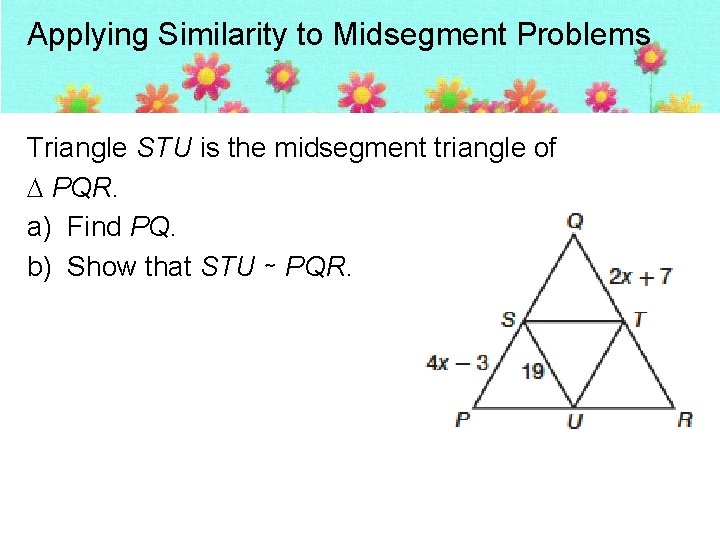
Applying Similarity to Midsegment Problems Triangle STU is the midsegment triangle of PQR. a) Find PQ. b) Show that STU ∼ PQR.

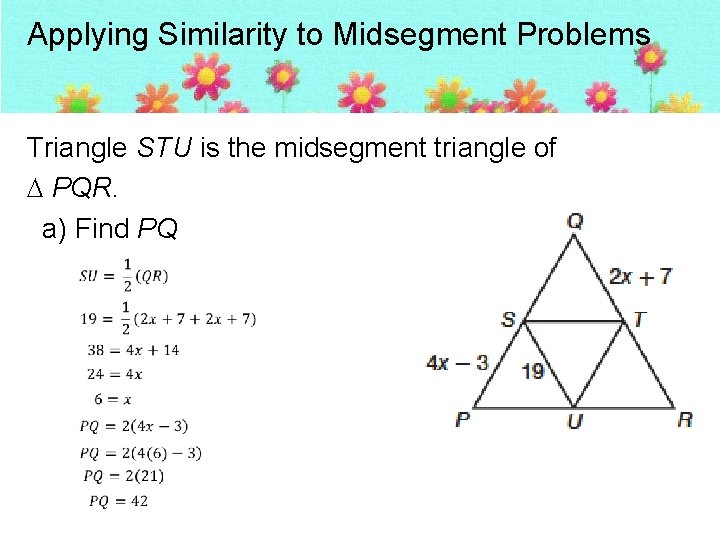
Applying Similarity to Midsegment Problems Triangle STU is the midsegment triangle of PQR. a) Find PQ

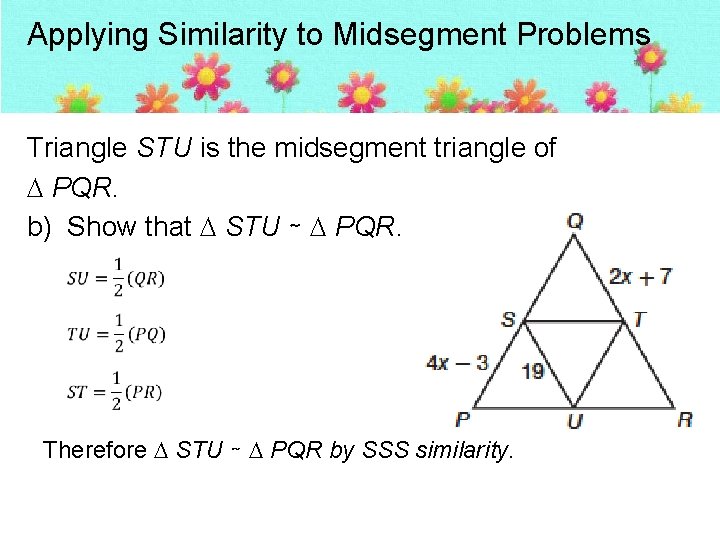
Applying Similarity to Midsegment Problems Triangle STU is the midsegment triangle of PQR. b) Show that STU ∼ PQR. Therefore STU ∼ PQR by SSS similarity.

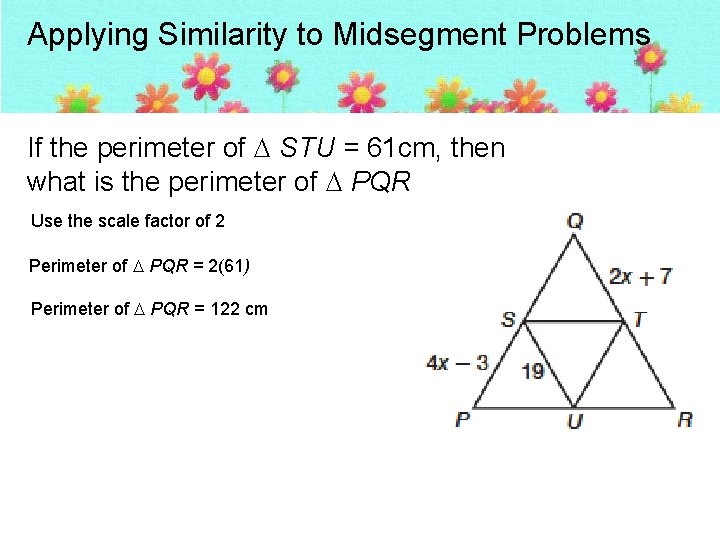
Applying Similarity to Midsegment Problems If the perimeter of STU = 61 cm, then what is the perimeter of PQR Use the scale factor of 2 Perimeter of PQR = 2(61) Perimeter of PQR = 122 cm

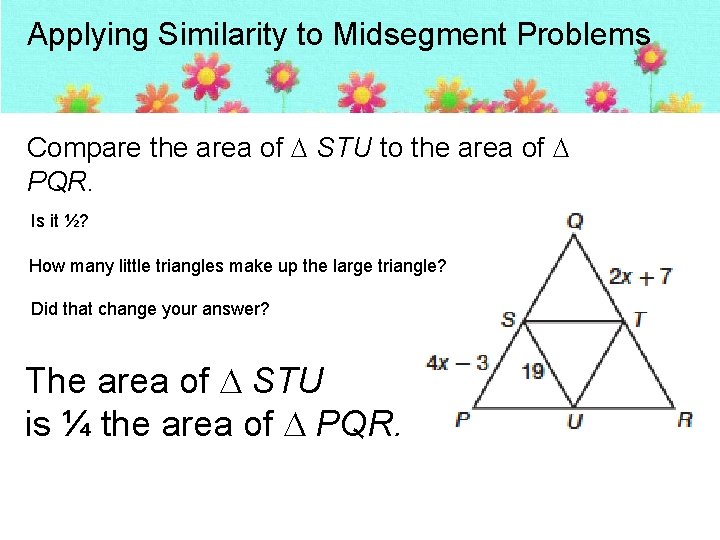
Applying Similarity to Midsegment Problems Compare the area of STU to the area of PQR. Is it ½? How many little triangles make up the large triangle? Did that change your answer? The area of STU is ¼ the area of PQR.

Any questions? 1. What is a midsegment of a triangle? 2. Which of the side lengths of a triangle is the midsegment’s length half of? 3. Which of the side lengths of a triangle is the midsegment parallel to? 4. How is a midsegment triangle related to the original triangle?