TRIANGLE CONGRUENCE IDENTIFYING TYPES AND PROOFS USING THEOREMS










- Slides: 18

TRIANGLE CONGRUENCE IDENTIFYING TYPES AND PROOFS USING THEOREMS

• Side-Side (SSS) Postulate If the three sides of one triangle are congruent to the three sides of another triangle, then the two triangles are congruent. 4 2 3 3 4 2

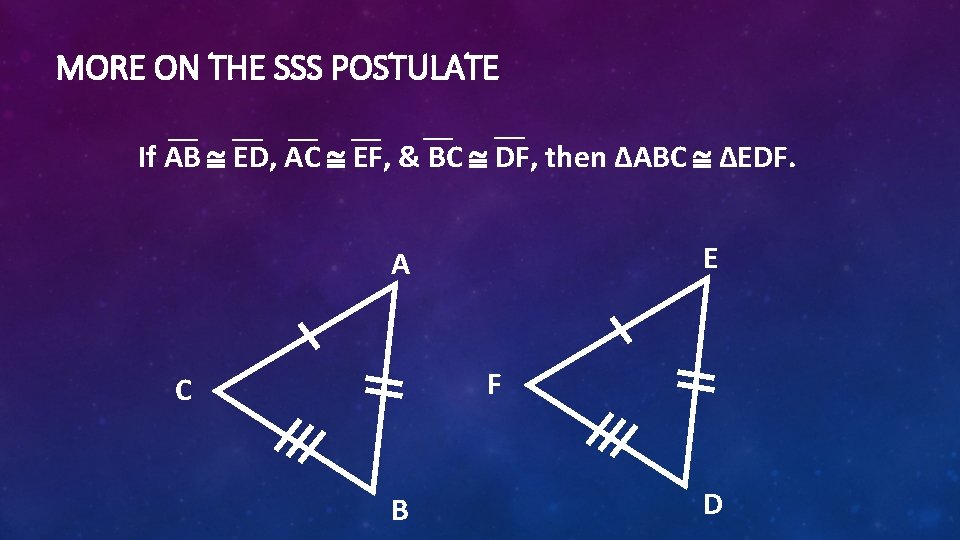
MORE ON THE SSS POSTULATE If AB ED, AC EF, & BC DF, then ΔABC ΔEDF. E A F C B D

SIDE-ANGLE-SIDE (SAS) POSTULATE If two sides and the included angle of one triangle is congruent to two sides and the included angle of another triangle, then the two triangles are congruent. 2 2 110° 4 4

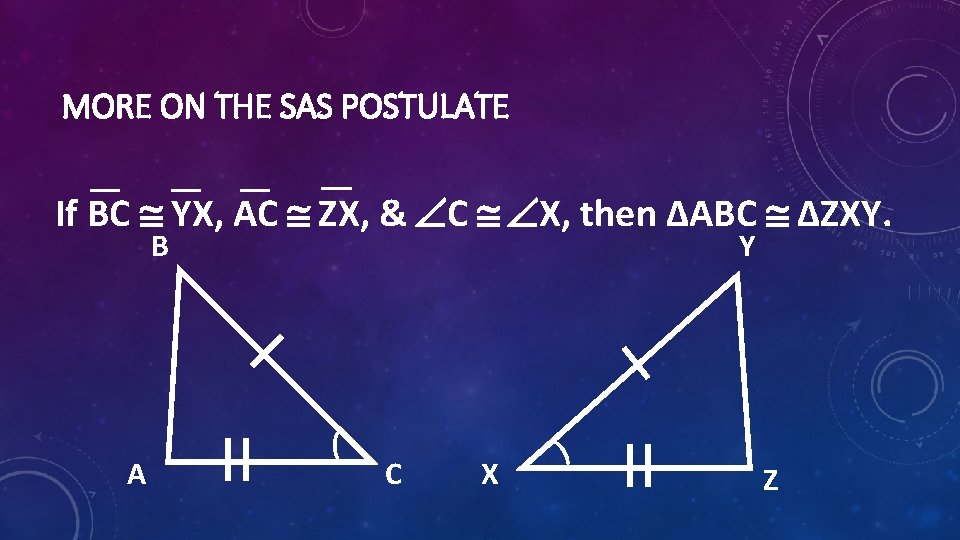
MORE ON THE SAS POSTULATE If BC YX, AC ZX, & C X, then ΔABC ΔZXY. B A Y ( C X ) Z

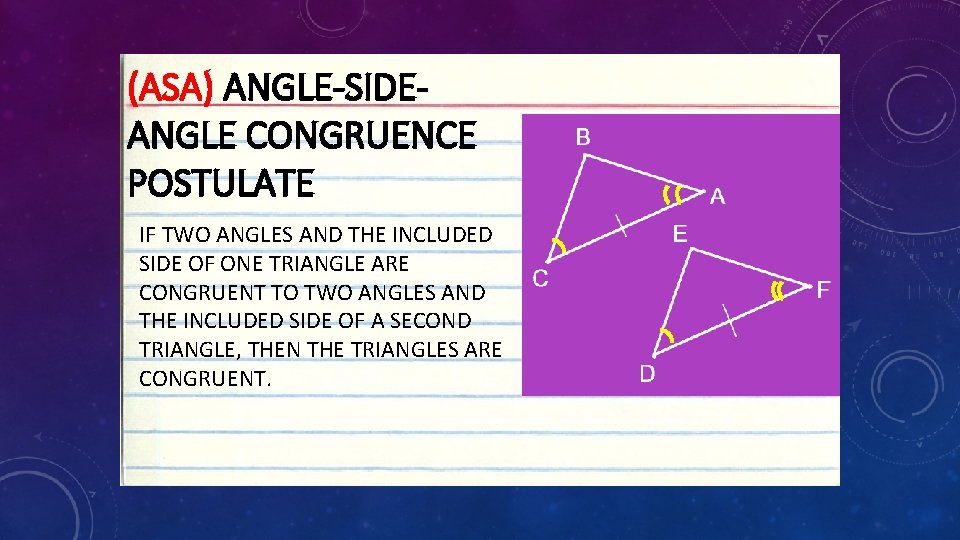
(ASA) ANGLE-SIDEANGLE CONGRUENCE POSTULATE IF TWO ANGLES AND THE INCLUDED SIDE OF ONE TRIANGLE ARE CONGRUENT TO TWO ANGLES AND THE INCLUDED SIDE OF A SECOND TRIANGLE, THEN THE TRIANGLES ARE CONGRUENT.

EXAMPLE 1 Which Postulate can you use to prove the triangles congruent? A) SSS Postulate B) SAS Postulate C) ASA Postulate D) not congruent

EXAMPLE 2 Which Postulate can you use to prove the triangles congruent? A) SSS Postulate B) SAS Postulate C) ASA Postulate D) not congruent

EXAMPLE 3 Which Postulate can you use to prove the triangles congruent? A) SSS Postulate B) SAS Postulate C) ASA Postulate D) not congruent

EXAMPLE 4 Which Postulate can you use to prove the triangles congruent? A) SSS Postulate B) SAS Postulate C) ASA Postulate D) not congruent

EXAMPLE 5 Which Postulate can you use to prove the triangles congruent? A) SSS Postulate B) SAS Postulate C) ASA Postulate D) not congruent

EXAMPLE 6 Which Postulate can you use to prove the triangles congruent? A) SSS Postulate B) SAS Postulate C) ASA Postulate D) not congruent

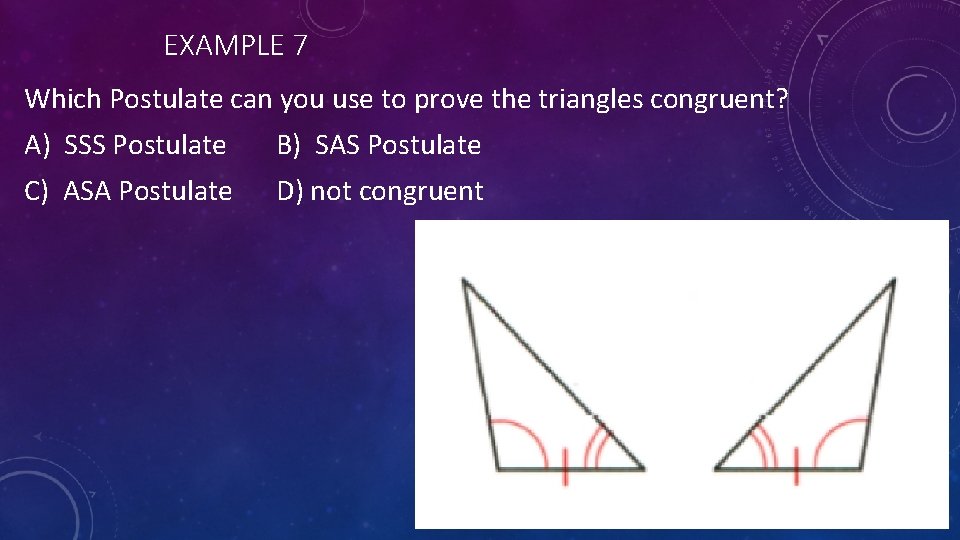
EXAMPLE 7 Which Postulate can you use to prove the triangles congruent? A) SSS Postulate B) SAS Postulate C) ASA Postulate D) not congruent

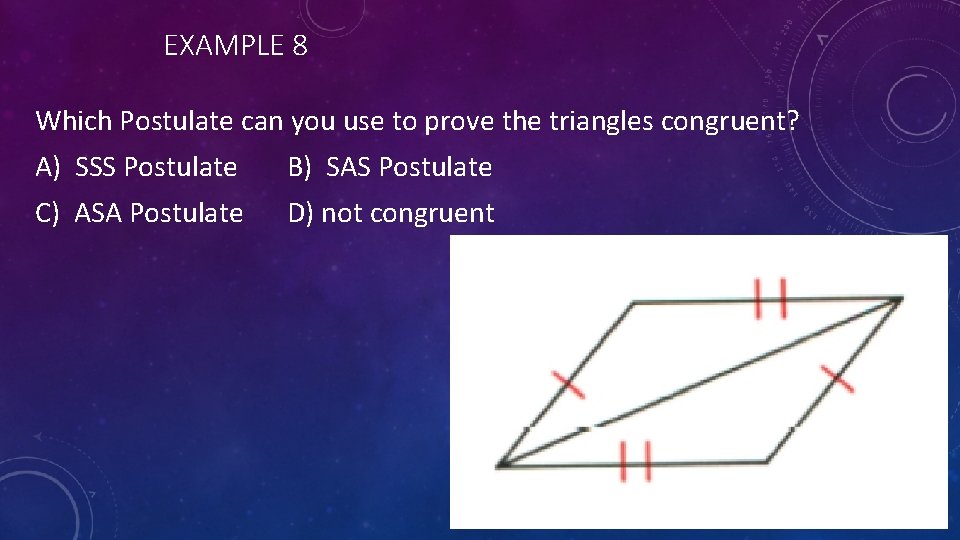
EXAMPLE 8 Which Postulate can you use to prove the triangles congruent? A) SSS Postulate B) SAS Postulate C) ASA Postulate D) not congruent

Intro to Proofs

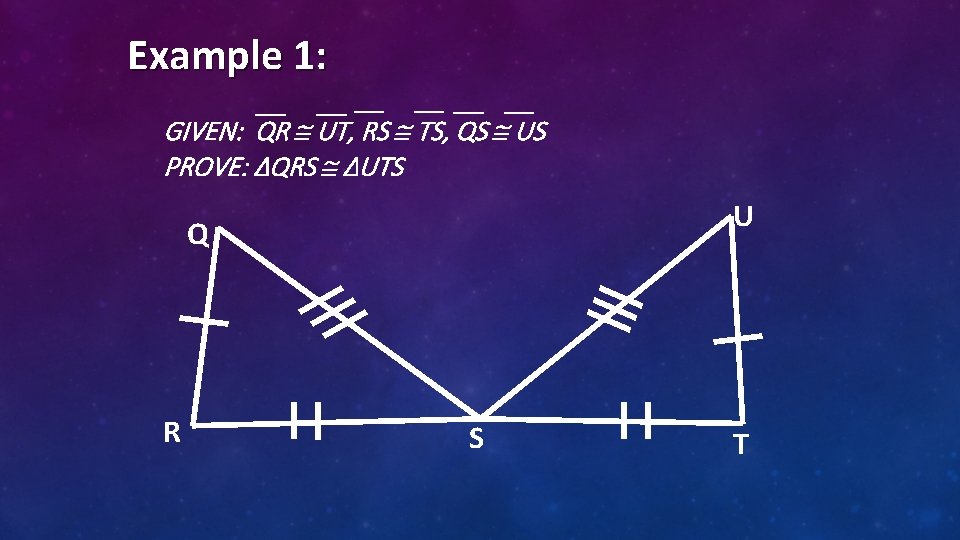
Example 1: GIVEN: QR UT, RS TS, QS US PROVE: ΔQRS ΔUTS U Q R S T

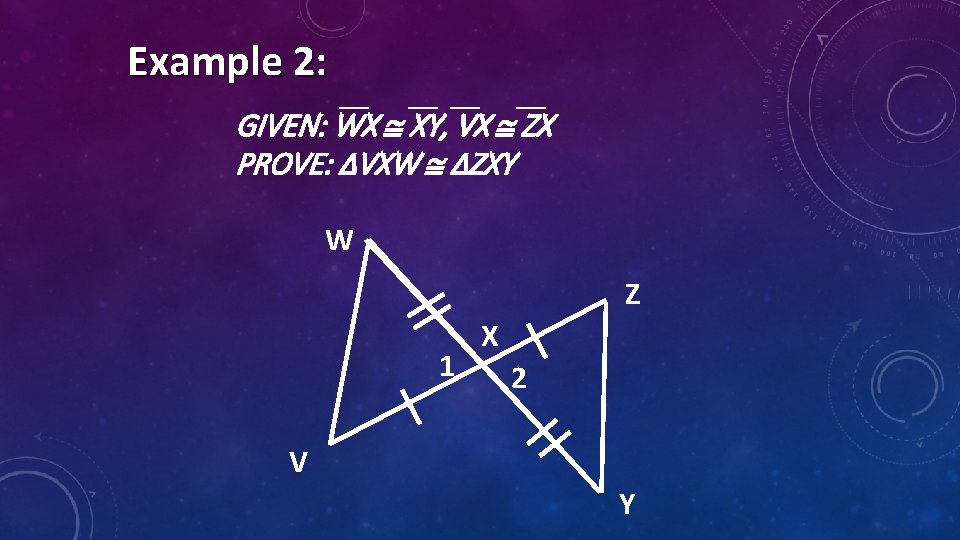
Example 2: GIVEN: WX XY, VX ZX PROVE: ΔVXW ΔZXY W Z 1 X 2 V Y

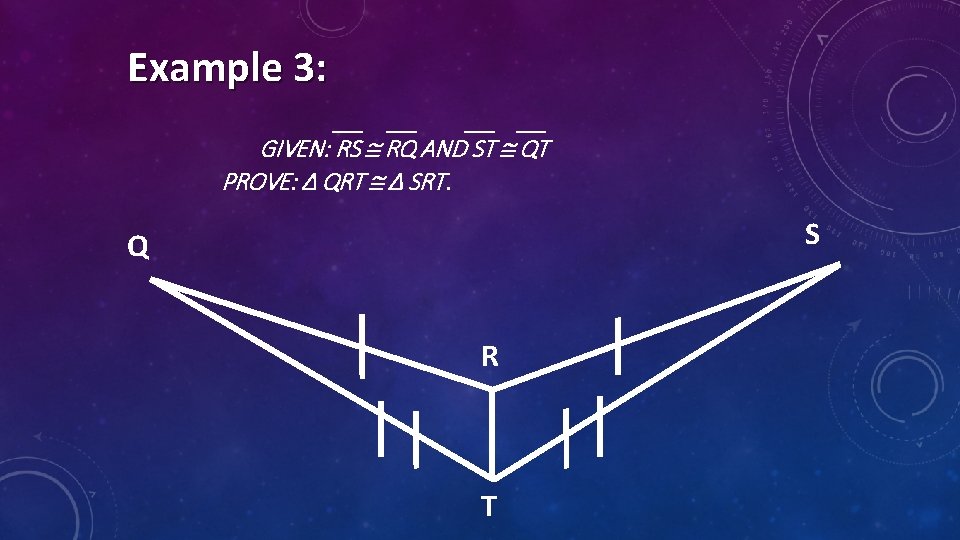
Example 3: GIVEN: RS RQ AND ST QT PROVE: Δ QRT Δ SRT. S Q R T