TRGONOMETR y 3 sin 5 x cos 4

  • Slides: 26
Download presentation
TRİGONOMETRİ

TRİGONOMETRİ

y 3 sin= 5 x cos= 4 Sinüs sin Kosinüs cos Tanjant tan Kotanjant

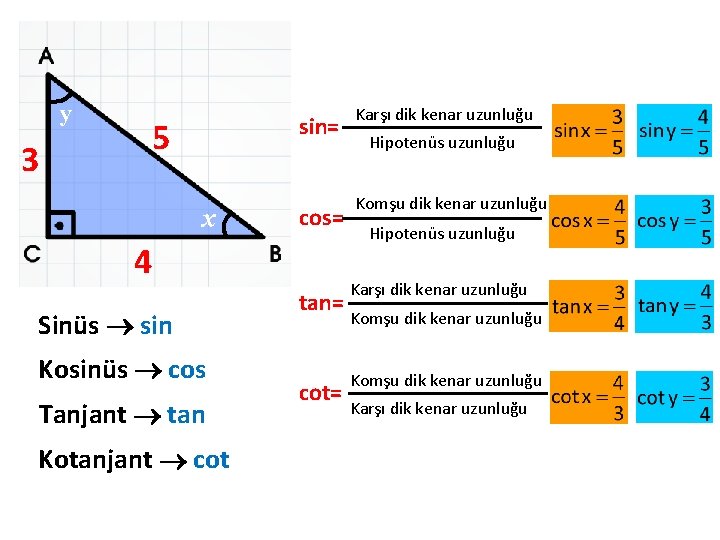
y 3 sin= 5 x cos= 4 Sinüs sin Kosinüs cos Tanjant tan Kotanjant cot Karşı dik kenar uzunluğu Hipotenüs uzunluğu Komşu dik kenar uzunluğu Hipotenüs uzunluğu tan= Karşı dik kenar uzunluğu cot= Komşu dik kenar uzunluğu Karşı dik kenar uzunluğu

Örnek: 5 13 12 Çözüm: Şekildeki dik üçgende x açısının trigonometrik oranlarını yazınız. x

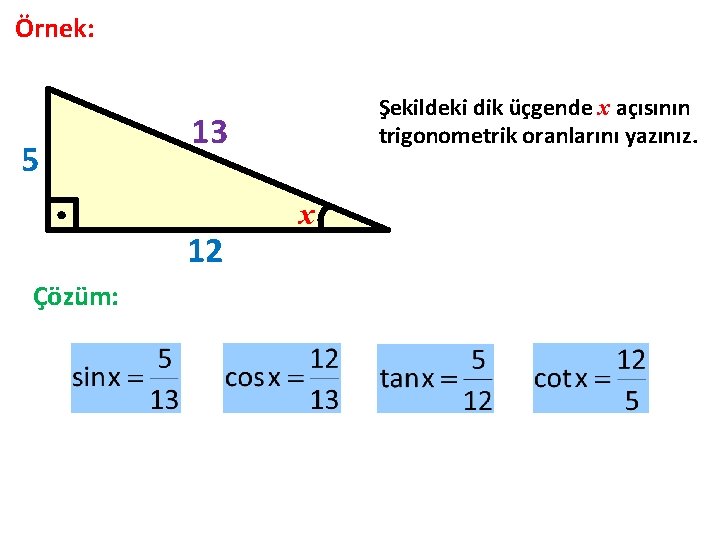
Örnek: 5 13 12 Çözüm: Şekildeki dik üçgende x açısının trigonometrik oranlarını yazınız. x

Örnek: Bir dik üçgende 0 o x 90 o olmak üzere; ise sinx, cosx

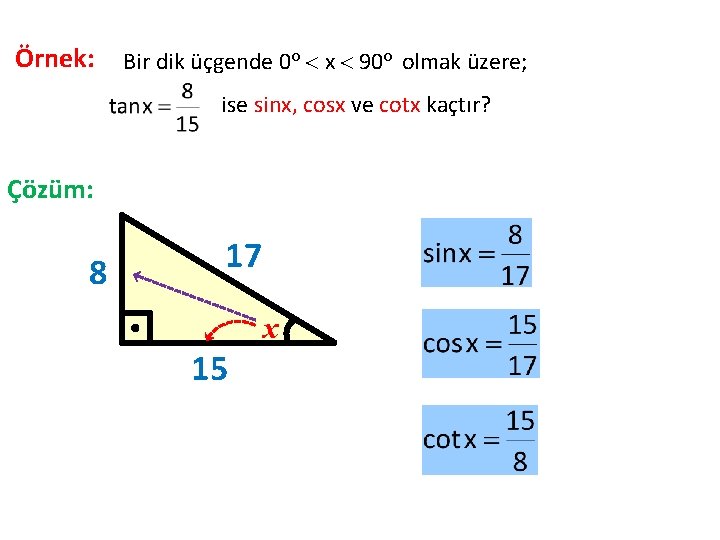
Örnek: Bir dik üçgende 0 o x 90 o olmak üzere; ise sinx, cosx ve cotx kaçtır? Çözüm: 8 17 x 15

Örnek: Bir dik üçgende 0 o x 90 o olmak üzere; ise sinx ve

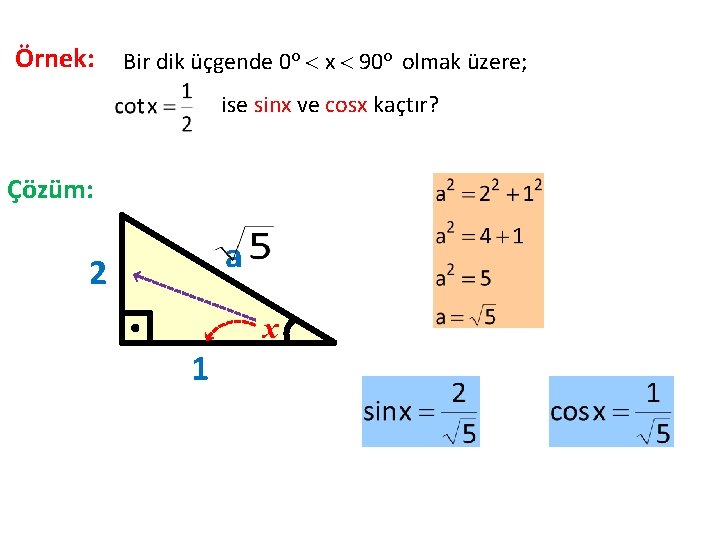
Örnek: Bir dik üçgende 0 o x 90 o olmak üzere; ise sinx ve cosx kaçtır? Çözüm: a 2 x 1

Örnek: A 20 12 C Çözüm: Şekildeki dik üçgende |AB|=20 cm ve x 16

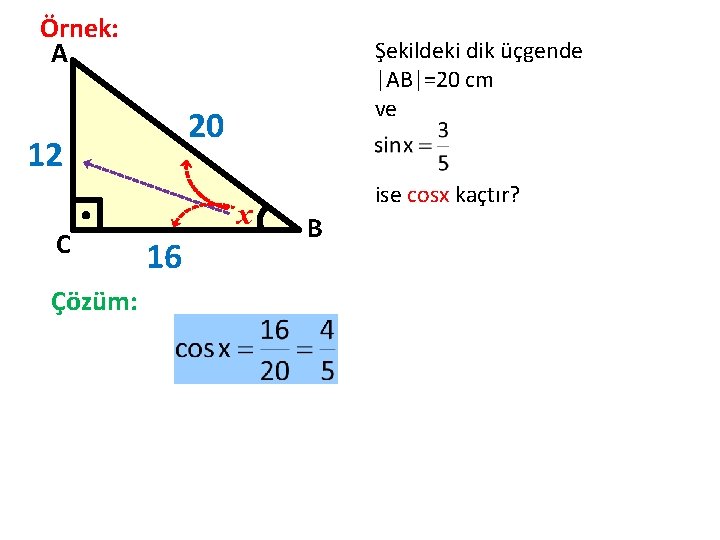
Örnek: A 20 12 C Çözüm: Şekildeki dik üçgende |AB|=20 cm ve x 16 ise cosx kaçtır? B

A Örnek: Çözüm: 4 5 y C x 5 D Şekildeki dik üçgende |AD|=|DC|

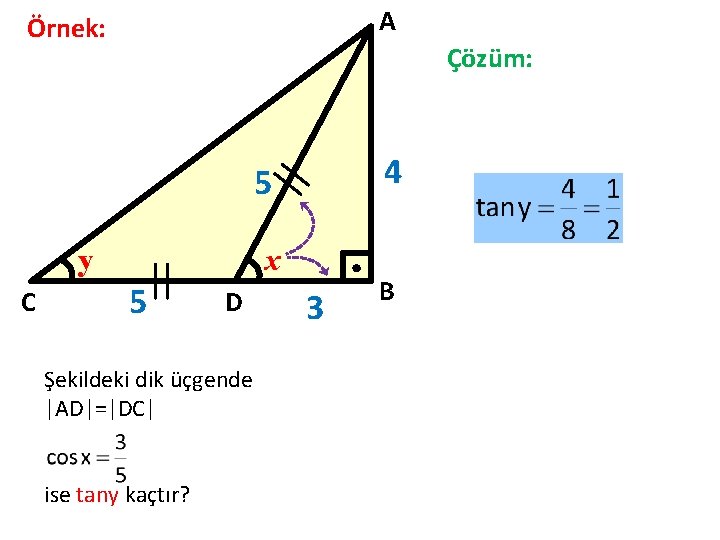
A Örnek: Çözüm: 4 5 y C x 5 D Şekildeki dik üçgende |AD|=|DC| ise tany kaçtır? 3 B

TRİGONOMETRİK ORANLARIN BİRBİRLERİYLE OLAN İLİŞKİLERİ

TRİGONOMETRİK ORANLARIN BİRBİRLERİYLE OLAN İLİŞKİLERİ

1 y 3 5 x 4 x + y = 90 o Not: Birbirini

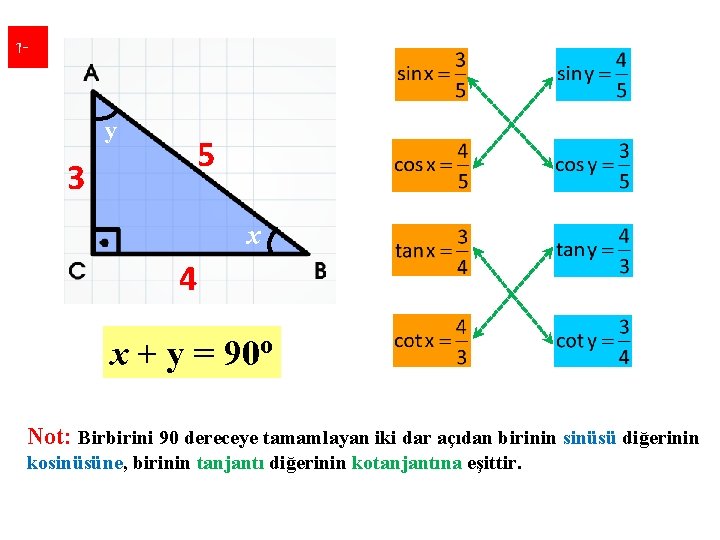
1 y 3 5 x 4 x + y = 90 o Not: Birbirini 90 dereceye tamamlayan iki dar açıdan birinin sinüsü diğerinin kosinüsüne, birinin tanjantı diğerinin kotanjantına eşittir.

Örnek: sin 20 o = cos 70 o cos 37 o = sin 53

Örnek: sin 20 o = cos 70 o cos 37 o = sin 53 o tan 55 o = cot 35 o cot 62 o = tan 28 o

Örnek: Çözüm: sin 10 o = cos 80 o işleminin sonucu kaçtır?

Örnek: Çözüm: sin 10 o = cos 80 o işleminin sonucu kaçtır?

Örnek: Çözüm: tan 65 o = cot 25 o işleminin sonucu kaçtır?

Örnek: Çözüm: tan 65 o = cot 25 o işleminin sonucu kaçtır?

2 y 3 5 x 4

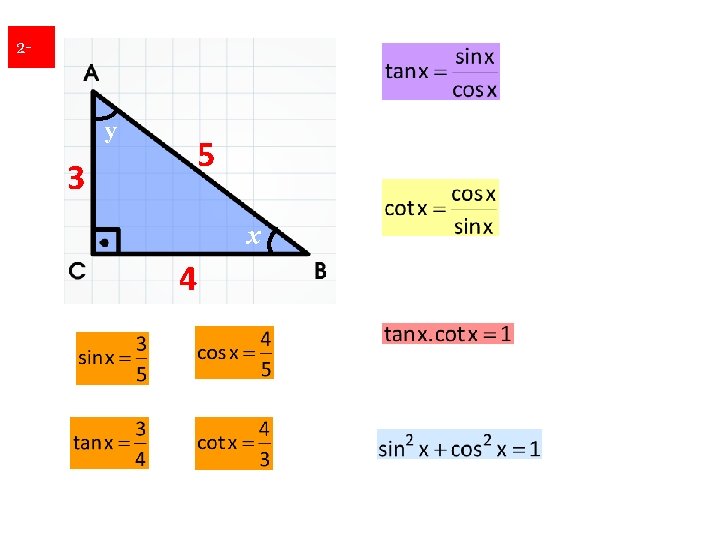
2 y 3 5 x 4

Örnek: Çözüm: Bir dik üçgende 0 o x 90 o olmak üzere; 4. sinx

Örnek: Çözüm: Bir dik üçgende 0 o x 90 o olmak üzere; 4. sinx = 9. cosx ise tanx kaçtır?

o o o 30 , 60 VE 45 LİK AÇILARIN TRİGONOMETRİK ORANLARI

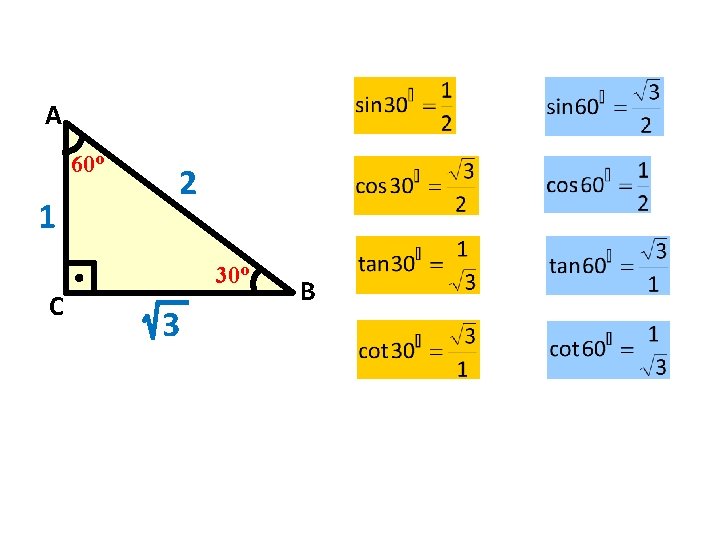
o o o 30 , 60 VE 45 LİK AÇILARIN TRİGONOMETRİK ORANLARI

A 60 o 1 2 30 o C 3 B

A 60 o 1 2 30 o C 3 B

A 45 o 2 1 C 45 o 1 B Not: Trigonometri sorularında 30,

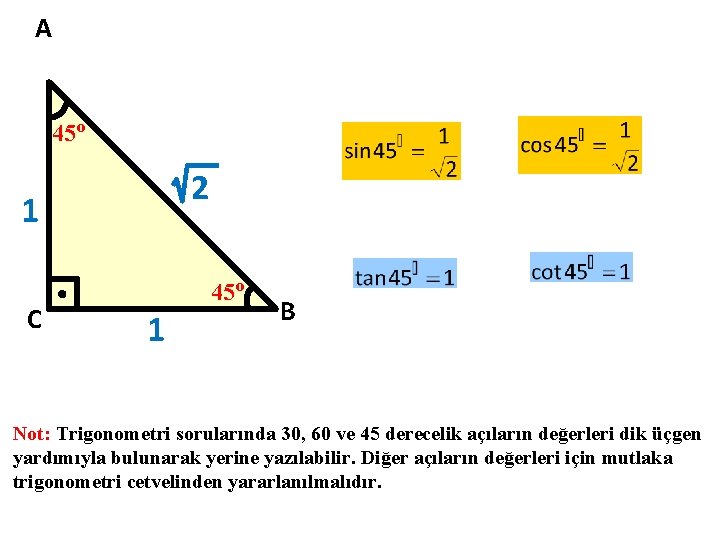
A 45 o 2 1 C 45 o 1 B Not: Trigonometri sorularında 30, 60 ve 45 derecelik açıların değerleri dik üçgen yardımıyla bulunarak yerine yazılabilir. Diğer açıların değerleri için mutlaka trigonometri cetvelinden yararlanılmalıdır.

Not: Trigonometrik oranlar tablosu incelenirse, aşağıdaki özelliklerle karşılaşılır. Bir dar açının ölçüsü artarsa; Øsinüs

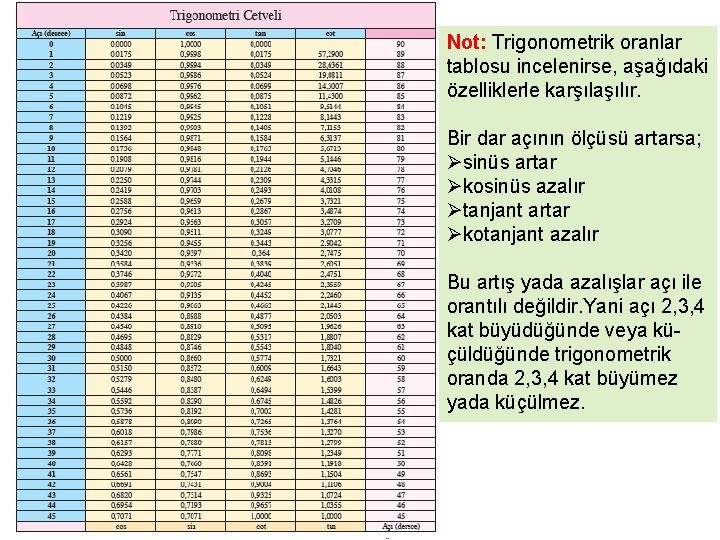
Not: Trigonometrik oranlar tablosu incelenirse, aşağıdaki özelliklerle karşılaşılır. Bir dar açının ölçüsü artarsa; Øsinüs artar Økosinüs azalır Øtanjant artar Økotanjant azalır Bu artış yada azalışlar açı ile orantılı değildir. Yani açı 2, 3, 4 kat büyüdüğünde veya küçüldüğünde trigonometrik oranda 2, 3, 4 kat büyümez yada küçülmez.

Örnek: tan 83 o , cot 2 o , tan 53 o ü küçükten

Örnek: tan 83 o , cot 2 o , tan 53 o ü küçükten büyüğe doğru sıralayınız. Örnek: sin 25 o , cos 35 o , sin 50 o yi küçükten büyüğe doğru sıralayınız.

Örnek:

Örnek:

Örnek: Çözüm:

Örnek: Çözüm:

Örnek: Çözüm:

Örnek: Çözüm:

Örnek: Çözüm:

Örnek: Çözüm:

Örnek: 3 2 x

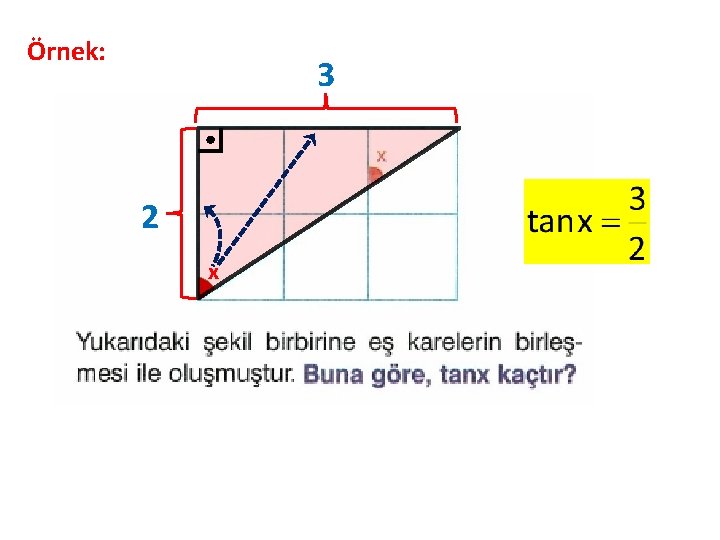
Örnek: 3 2 x

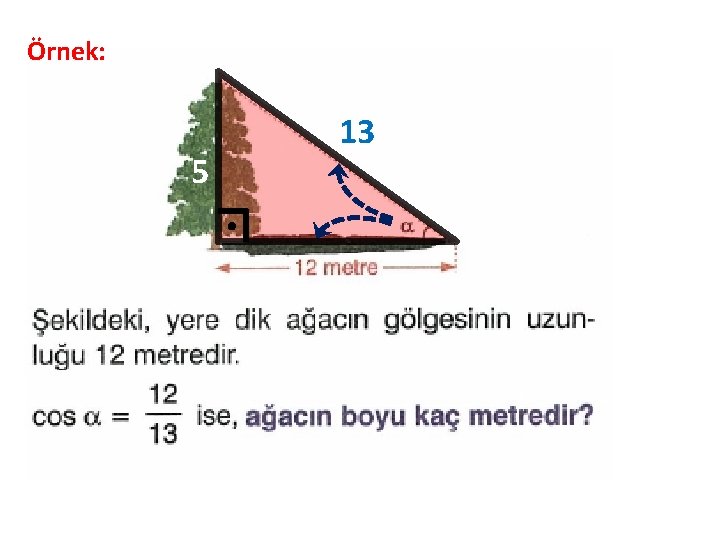
Örnek: 5 13

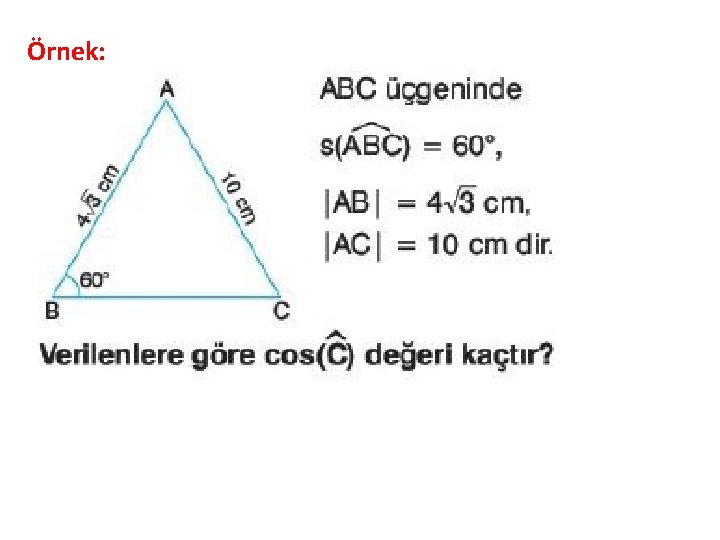
Örnek: 5 13

Örnek:

Örnek:

sin 2 sin sin cos sin cos 2sin 2 sin sin cos sin cos 2
sin sin Sin 2 sin 2 3 sinsin sin Sin 2 sin 2 3 sin
SIN SIN Definition of Sin Sin is anySIN SIN Definition of Sin Sin is any
2 sin A cos A 1 sin cos2 sin A cos A 1 sin cos
Sin animacin Sin animacin Sin animacin Sutil AparecerSin animacin Sin animacin Sin animacin Sutil Aparecer
Vino sin perros sin ruidos ni asalariados sinVino sin perros sin ruidos ni asalariados sin
sin s t sin s t 2 sinsin s t sin s t 2 sin
Vino sin perros sin ruidos ni asalariados sinVino sin perros sin ruidos ni asalariados sin
Sin An Overview Defining Sin Types of SinSin An Overview Defining Sin Types of Sin
Original Sin Original Sin Common Misconception Original SinOriginal Sin Original Sin Common Misconception Original Sin
Understanding Sin What is Sin Sin is aUnderstanding Sin What is Sin Sin is a
SIN What Is Sin Sin is the transgressionSIN What Is Sin Sin is the transgression
Vino sin perros sin ruidos ni asalariados sinVino sin perros sin ruidos ni asalariados sin
Sin Chapter Six The Nature of Sin SinSin Chapter Six The Nature of Sin Sin
sin 2 x cos x 1 0 sinsin 2 x cos x 1 0 sin
sin 2 x cos x 1 0 sinsin 2 x cos x 1 0 sin
3 Sin t x Cos t Sin t3 Sin t x Cos t Sin t
Example Simplify sin x sin x cos xExample Simplify sin x sin x cos x
sinx y sin x cos y cos xsinx y sin x cos y cos x
3 cos cos sin y y P 43 cos cos sin y y P 4
TRGONOMETR Elif Kabasakal Kazanmlar A l birimlerini tanrTRGONOMETR Elif Kabasakal Kazanmlar A l birimlerini tanr
EXCEL FORMLLERFONKSYON LAR MATEMATK TRGONOMETR n TOPLA BamszEXCEL FORMLLERFONKSYON LAR MATEMATK TRGONOMETR n TOPLA Bamsz
TRGONOMETR AI LLER TERS AI AI D ATRGONOMETR AI LLER TERS AI AI D A
TRGONOMETR KAYNAK LSE2 Matematik Ders Kitab n SayfaTRGONOMETR KAYNAK LSE2 Matematik Ders Kitab n Sayfa