TreeStructured Indexes Content based on Chapter 10 Database

Tree-Structured Indexes Content based on Chapter 10 Database Management Systems, (3 rd Edition), by Raghu Ramakrishnan and Johannes Gehrke. Mc. Graw Hill, 2003

B+-Tree Index Files B+-tree indices are an alternative to indexed-sequential files. v v Disadvantage of indexed-sequential files § performance degrades as file grows, since many overflow blocks get created. § Periodic reorganization of entire file is required. Advantage of B+-tree index files: § automatically reorganizes itself with small, local, changes, in the face of insertions and deletions. § Reorganization of entire file is not required to maintain performance. (Minor) disadvantage of B+-trees: § extra insertion and deletion overhead, space overhead. Advantages of B+-trees outweigh disadvantages § B+-trees are used extensively

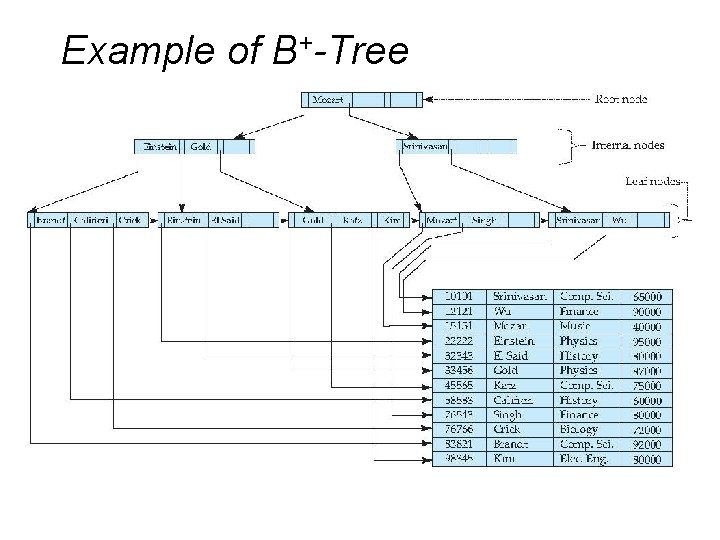
Example of B+-Tree

B+-Tree Node Structure v v Typical node § Ki are the search-key values § Pi are pointers to children (for non-leaf nodes) or pointers to records or buckets of records (for leaf nodes). The search-keys in a node are ordered K 1 < K 2 < K 3 <. . . < Kn– 1 (Initially assume no duplicate keys, address duplicates later)

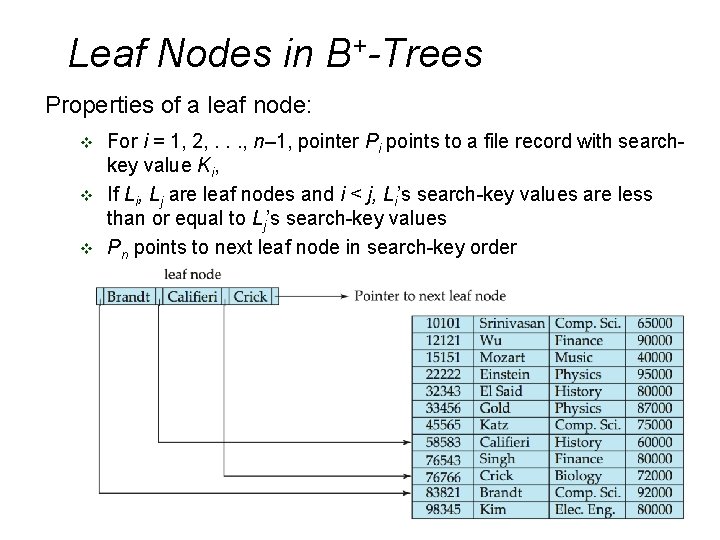
Leaf Nodes in B+-Trees Properties of a leaf node: v v v For i = 1, 2, . . . , n– 1, pointer Pi points to a file record with searchkey value Ki, If Li, Lj are leaf nodes and i < j, Li’s search-key values are less than or equal to Lj’s search-key values Pn points to next leaf node in search-key order

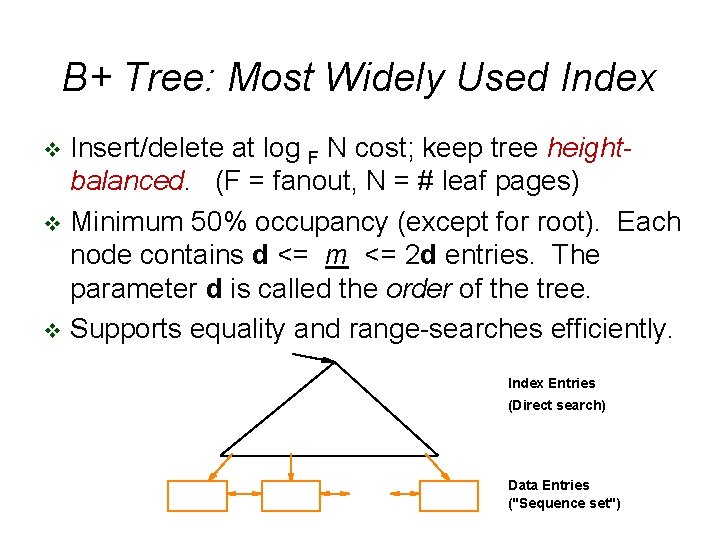
B+ Tree: Most Widely Used Index Insert/delete at log F N cost; keep tree heightbalanced. (F = fanout, N = # leaf pages) v Minimum 50% occupancy (except for root). Each node contains d <= m <= 2 d entries. The parameter d is called the order of the tree. v Supports equality and range-searches efficiently. v Index Entries (Direct search) Data Entries ("Sequence set")

Observations about B+-trees v v Since the inter-node connections are done by pointers, “logically” close blocks need not be “physically” close. The non-leaf levels of the B+-tree form a hierarchy of sparse indices. The B+-tree contains a relatively small number of levels • Level below root has at least 2* n/2 values • Next level has at least 2* n/2 values • . . etc. § If there are K search-key values in the file, the tree height is no more than log n/2 (K) § thus searches can be conducted efficiently. Insertions and deletions to the main file can be handled efficiently, as the index can be restructured in logarithmic time.

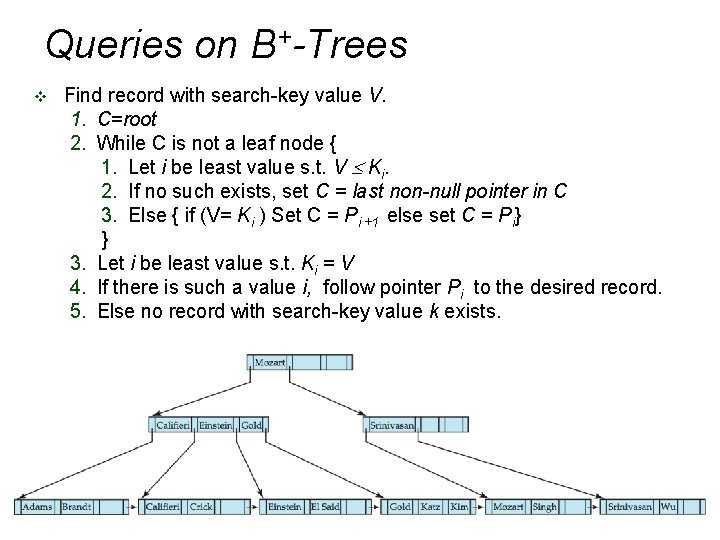
Queries on B+-Trees v Find record with search-key value V. 1. C=root 2. While C is not a leaf node { 1. Let i be least value s. t. V Ki. 2. If no such exists, set C = last non-null pointer in C 3. Else { if (V= Ki ) Set C = Pi +1 else set C = Pi} } 3. Let i be least value s. t. Ki = V 4. If there is such a value i, follow pointer Pi to the desired record. 5. Else no record with search-key value k exists.

Queries on B+-Trees (Cont. ) v v If there are K search-key values in the file, the height of the tree is no more than log n/2 (K). A node is generally the same size as a disk block, typically 4 kilobytes § and n is typically around 100 (40 bytes per index entry). With 1 million search key values and n = 100 § at most log 50(1, 000) = 4 nodes are accessed in a lookup. Contrast this with a balanced binary tree with 1 million search key values — around 20 nodes are accessed in a lookup § above difference is significant since every node access may need a disk I/O, costing around 20 milliseconds

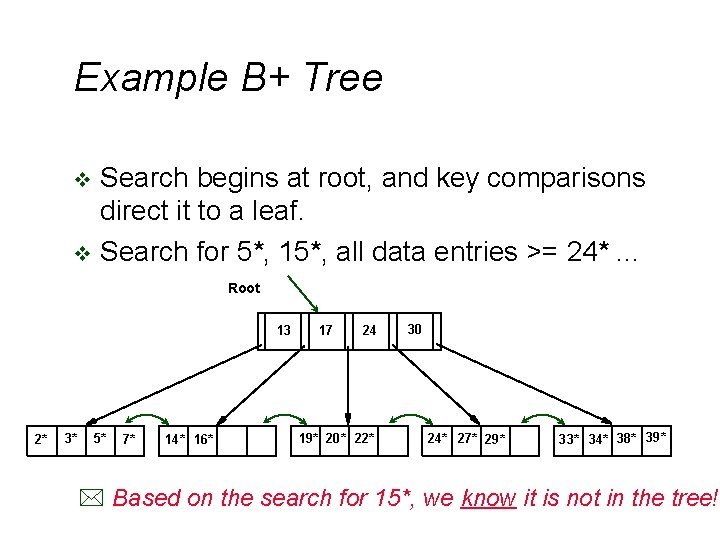
Example B+ Tree Search begins at root, and key comparisons direct it to a leaf. v Search for 5*, 15*, all data entries >= 24*. . . v Root 13 2* 3* 5* 7* 14* 16* 17 24 19* 20* 22* 30 24* 27* 29* 33* 34* 38* 39* * Based on the search for 15*, we know it is not in the tree!

B+ Trees in Practice v Typical order: 100. Typical fill-factor: 67%. § v Typical capacities: § § v average fanout = 133 Height 4: 1334 = 312, 900, 700 records Height 3: 1333 = 2, 352, 637 records Can often hold top levels in buffer pool: § § § Level 1 = 1 page = 8 Kbytes Level 2 = 133 pages = 1 Mbyte Level 3 = 17, 689 pages = 133 MBytes

Inserting a Data Entry into a B+ Tree Find correct leaf L. v Put data entry onto L. v § § If L has enough space, done! Else, must split L (into L and a new node L 2) • Redistribute entries evenly, copy up middle key. • Insert index entry pointing to L 2 into parent of L. v This can happen recursively § v To split index node, redistribute entries evenly, but push up middle key. (Contrast with leaf splits. ) Splits “grow” tree; root split increases height. § Tree growth: gets wider or one level taller at top.

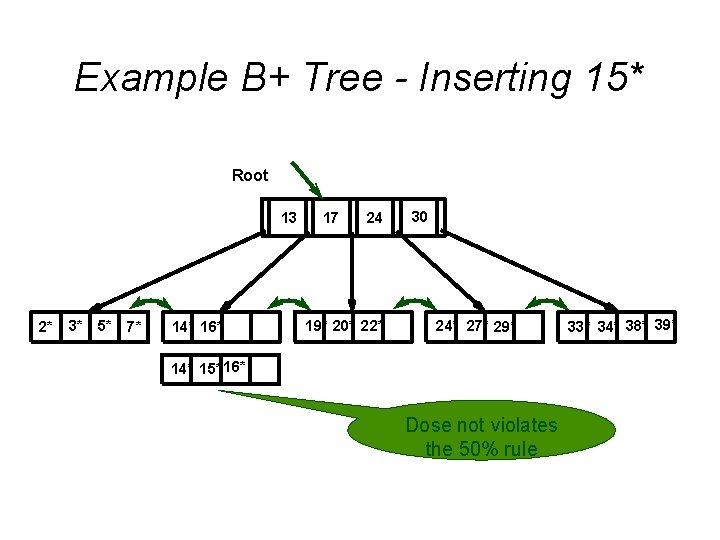
Example B+ Tree - Inserting 15* Root 13 2* 3* 5* 7* 14* 16* 17 24 19* 20* 22* 30 24* 27* 29* 14* 15* 16* Dose not violates the 50% rule 33* 34* 38* 39*

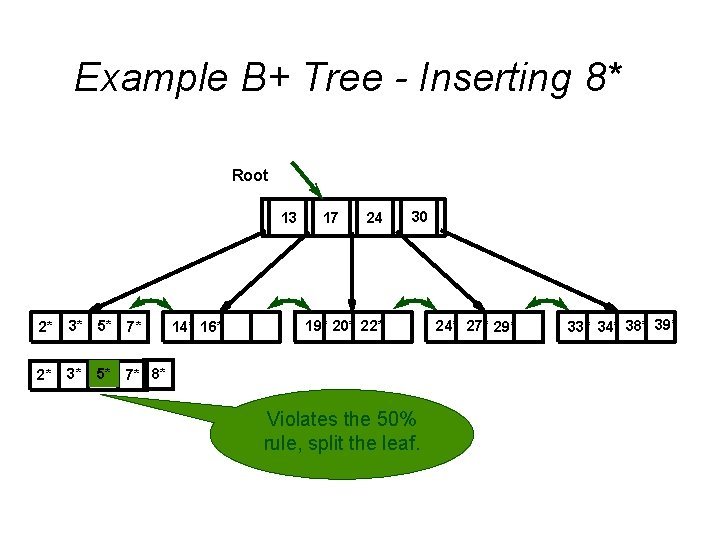
Example B+ Tree - Inserting 8* Root 13 2* 3* 5* 7* 8* 14* 16* 17 24 30 19* 20* 22* Violates the 50% rule, split the leaf. 24* 27* 29* 33* 34* 38* 39*

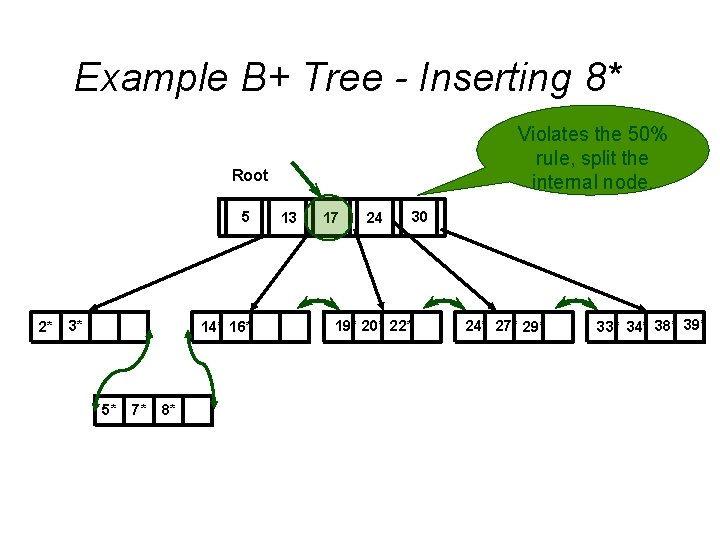
Example B+ Tree - Inserting 8* Violates the 50% rule, split the internal node. Root 5 2* 3* 14* 16* 5* 7* 8* 13 17 24 30 19* 20* 22* 24* 27* 29* 33* 34* 38* 39*

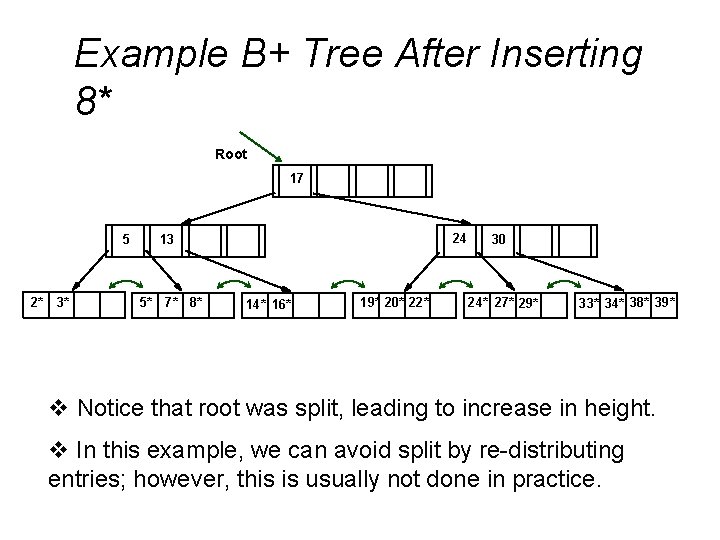
Example B+ Tree After Inserting 8* Root 17 5 2* 3* 24 13 5* 7* 8* 14* 16* 19* 20* 22* 30 24* 27* 29* 33* 34* 38* 39* v Notice that root was split, leading to increase in height. v In this example, we can avoid split by re-distributing entries; however, this is usually not done in practice.

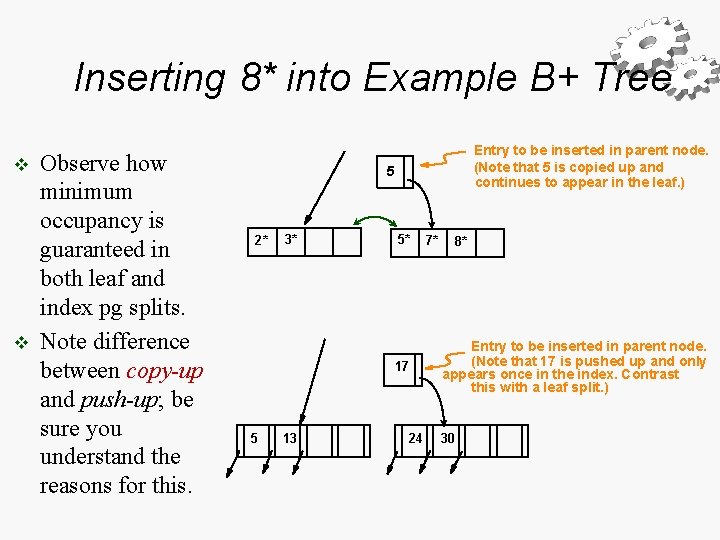
Inserting 8* into Example B+ Tree v v Observe how minimum occupancy is guaranteed in both leaf and index pg splits. Note difference between copy-up and push-up; be sure you understand the reasons for this. Entry to be inserted in parent node. (Note that 5 is s copied up and continues to appear in the leaf. ) 5 2* 3* 5* 17 5 13 24 7* 8* Entry to be inserted in parent node. (Note that 17 is pushed up and only appears once in the index. Contrast this with a leaf split. ) 30

Deleting a Data Entry from a B+ Tree Start at root, find leaf L where entry belongs. v Remove the entry. v § § If L is at least half-full, done! If L has only d-1 entries, • Try to re-distribute, borrowing from siblings (adjacent nodes with same parent as L). • If re-distribution fails, merge L and sibling. If merge occurred, must delete entry (pointing to L or sibling) from parent of L. v Merge could propagate to root, decreasing height. v

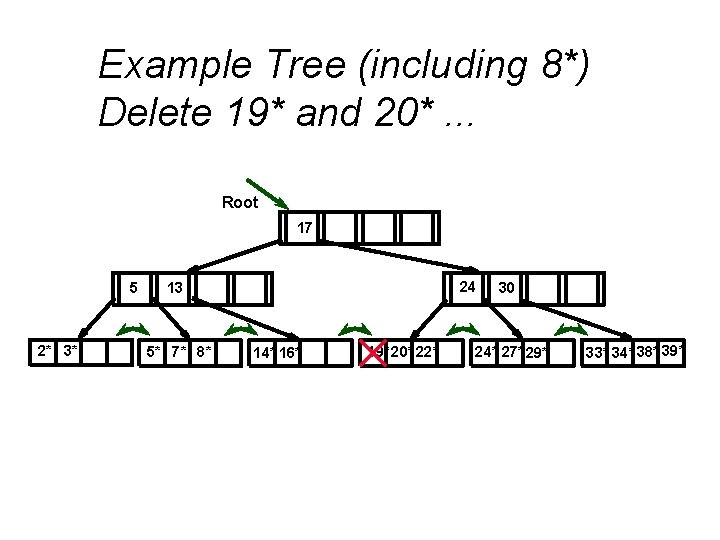
Example Tree (including 8*) Delete 19* and 20*. . . Root 17 5 2* 3* 24 13 5* 7* 8* 14* 16* 19* 20* 22* 30 24* 27* 29* 33* 34* 38* 39*

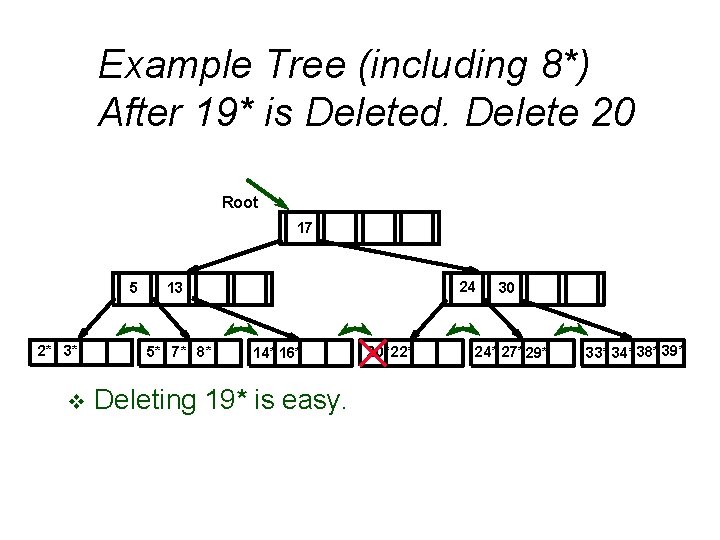
Example Tree (including 8*) After 19* is Deleted. Delete 20 Root 17 5 2* 3* v 24 13 5* 7* 8* 14* 16* Deleting 19* is easy. 20* 22* 30 24* 27* 29* 33* 34* 38* 39*

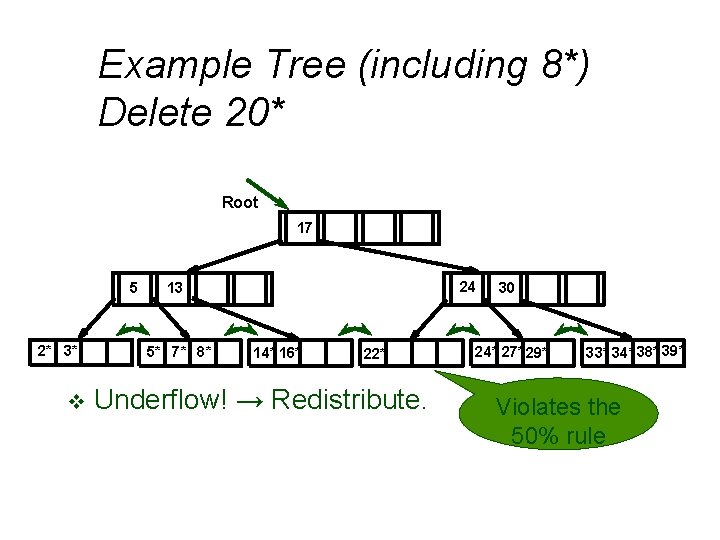
Example Tree (including 8*) Delete 20* Root 17 5 2* 3* v 24 13 5* 7* 8* 14* 16* 22* Underflow! → Redistribute. 30 24* 27* 29* 33* 34* 38* 39* Violates the 50% rule

Example Tree After (Inserting 8*, Then) Deleting 19* and 20*. . . Root 17 5 2* 3* v 27 13 5* 7* 8* 14* 16* 22* 24* 30 27* 29* 33* 34* 38* 39* Deleting 20* is done with re-distribution. Notice how the lowest key is copied up.

. . . And Then Deleting 24* Root 17 5 2* 3* 27 13 5* 7* 8* 14* 16* 22* 24* Underflow! v Can we do redistribution? v § MERGE! 30 27* 29* 33* 34* 38* 39*

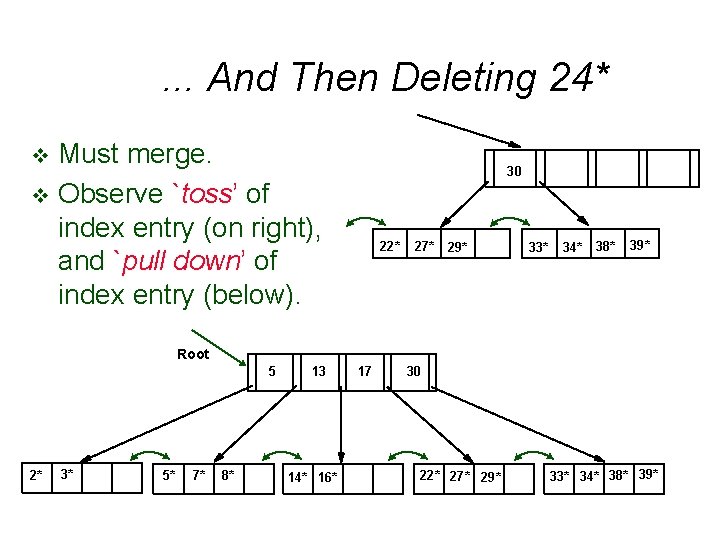
. . . And Then Deleting 24* Must merge. v Observe `toss’ of index entry (on right), and `pull down’ of index entry (below). v 30 22* 27* 29* 33* 34* 38* 39* Root 5 2* 3* 5* 7* 8* 13 14* 16* 17 30 22* 27* 29* 33* 34* 38* 39*

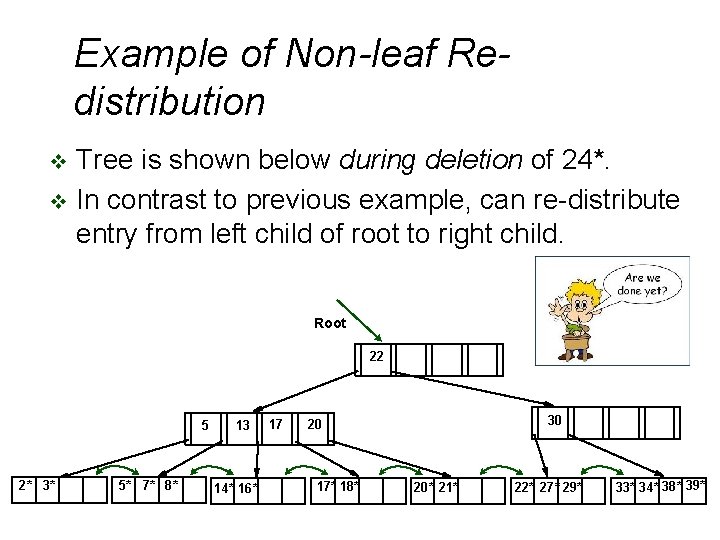
Example of Non-leaf Redistribution Tree is shown below during deletion of 24*. v In contrast to previous example, can re-distribute entry from left child of root to right child. v Root 22 5 2* 3* 5* 7* 8* 13 14* 16* 17 30 20 17* 18* 20* 21* 22* 27* 29* 33* 34* 38* 39*

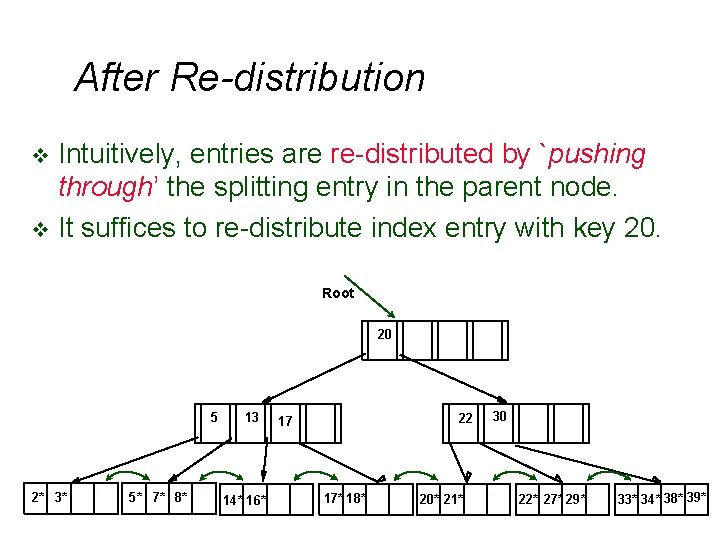
After Re-distribution Intuitively, entries are re-distributed by `pushing through’ the splitting entry in the parent node. v It suffices to re-distribute index entry with key 20. v Root 20 5 2* 3* 5* 7* 8* 13 14* 16* 22 17 17* 18* 20* 21* 30 22* 27* 29* 33* 34* 38* 39*

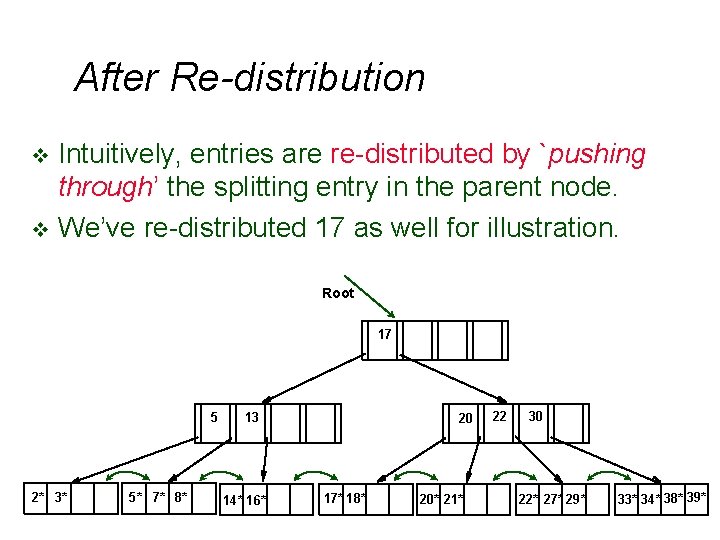
After Re-distribution Intuitively, entries are re-distributed by `pushing through’ the splitting entry in the parent node. v We’ve re-distributed 17 as well for illustration. v Root 17 5 2* 3* 5* 7* 8* 13 14* 16* 20 17* 18* 20* 21* 22 30 22* 27* 29* 33* 34* 38* 39*

Indexing Strings v v Variable length strings as keys § Variable fanout § Use space utilization as criterion for splitting, not number of pointers Prefix compression § Key values at internal nodes can be prefixes of full key • Keep enough characters to distinguish entries in the subtrees separated by the key value • E. g. “Silas” and “Silberschatz” can be separated by “Silb” § Keys in leaf node can be compressed by sharing common prefixes

Bulk Loading and Bottom-Up Build v Inserting entries one-at-a-time into a B+-tree requires 1 IO per entry § assuming leaf level does not fit in memory § can be very inefficient for loading a large number of entries at a time (bulk loading) v Efficient alternative 1: § sort entries first § insert in sorted order • insertion will go to existing page (or cause a split) • much improved IO performance, but most leaf nodes half full v Efficient alternative 2: Bottom-up B+-tree construction § As before sort entries § And then create tree layer-by-layer, starting with leaf level § Implemented as part of bulk-load utility by most database systems

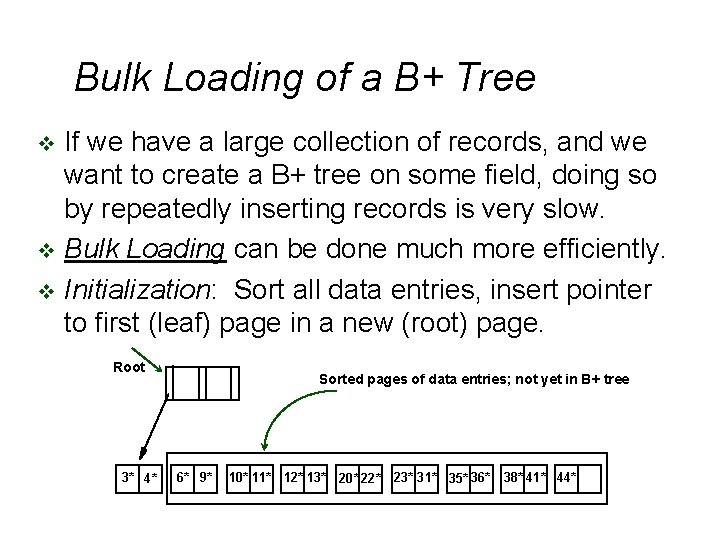
Bulk Loading of a B+ Tree If we have a large collection of records, and we want to create a B+ tree on some field, doing so by repeatedly inserting records is very slow. v Bulk Loading can be done much more efficiently. v Initialization: Sort all data entries, insert pointer to first (leaf) page in a new (root) page. v Root 3* 4* Sorted pages of data entries; not yet in B+ tree 6* 9* 10* 11* 12* 13* 20* 22* 23* 31* 35* 36* 38* 41* 44*

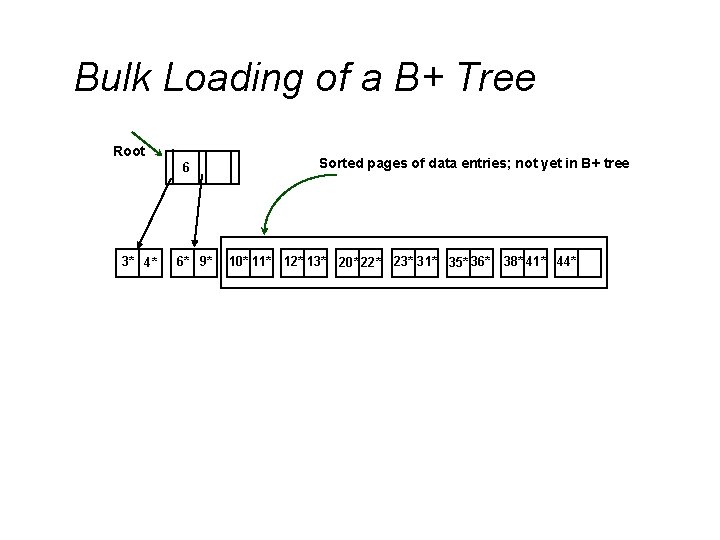
Bulk Loading of a B+ Tree Root 6 3* 4* 6* 9* Sorted pages of data entries; not yet in B+ tree 10* 11* 12* 13* 20* 22* 23* 31* 35* 36* 38* 41* 44*

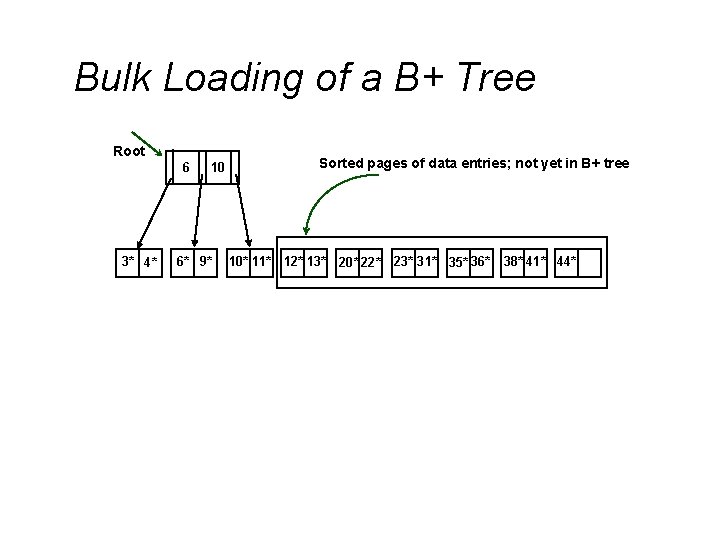
Bulk Loading of a B+ Tree Root 6 3* 4* 10 6* 9* Sorted pages of data entries; not yet in B+ tree 10* 11* 12* 13* 20* 22* 23* 31* 35* 36* 38* 41* 44*

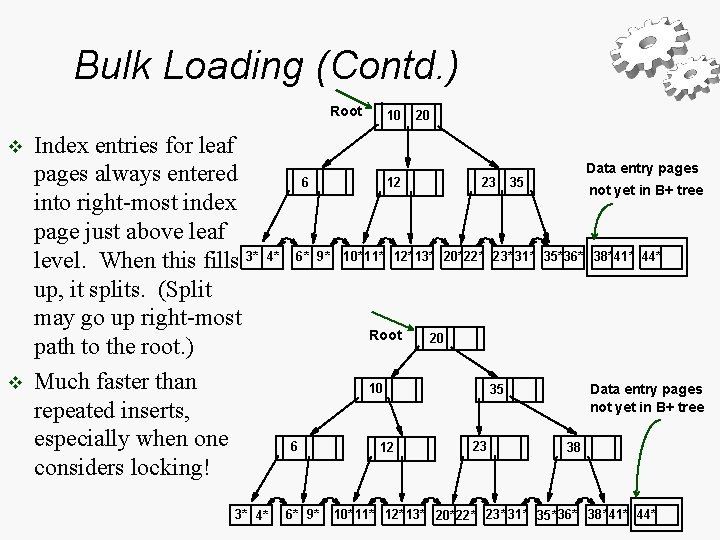
Bulk Loading (Contd. ) Root v v Index entries for leaf pages always entered into right-most index page just above leaf level. When this fills 3* up, it splits. (Split may go up right-most path to the root. ) Much faster than repeated inserts, especially when one considers locking! 10 6 4* 3* 4* 6* 9* 20 12 23 20 10 6* 9* not yet in B+ tree 10* 11* 12* 13* 20*22* 23* 31* 35* 36* 38*41* 44* Root 6 Data entry pages 35 12 Data entry pages not yet in B+ tree 35 23 38 10* 11* 12* 13* 20*22* 23* 31* 35* 36* 38*41* 44*

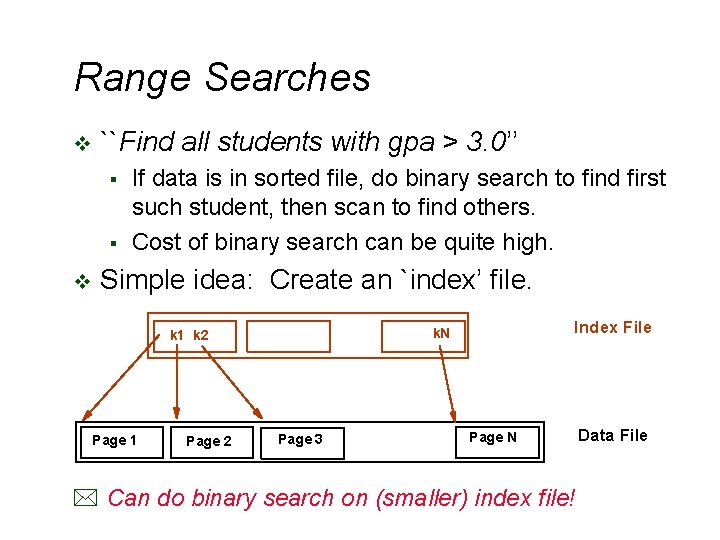
Range Searches v ``Find all students with gpa > 3. 0’’ § § v If data is in sorted file, do binary search to find first such student, then scan to find others. Cost of binary search can be quite high. Simple idea: Create an `index’ file. Page 1 Page 2 Index File k. N k 1 k 2 Page 3 Page N * Can do binary search on (smaller) index file! Data File

Animation v https: //www. cs. usfca. edu/~galles/visualization/BPlus. Tree. html