Trees Whats on the menu Terminology Basic Properties

Trees

What’s on the menu? Terminology Basic Properties Pointer-based implementation Algorithms

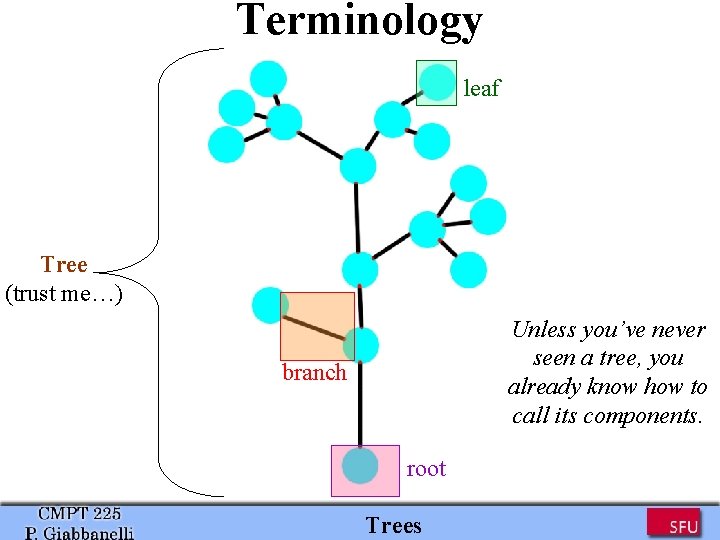
Terminology leaf Tree (trust me…) Unless you’ve never seen a tree, you already know how to call its components. branch root Trees

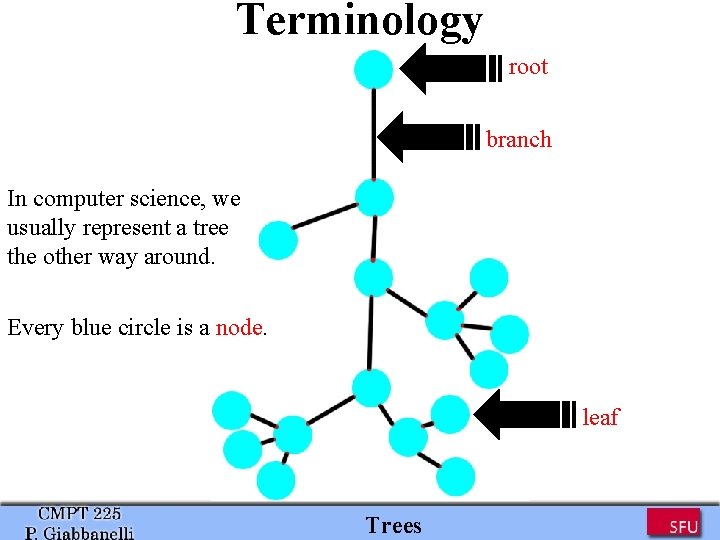
Terminology root branch In computer science, we usually represent a tree the other way around. Every blue circle is a node. leaf Trees

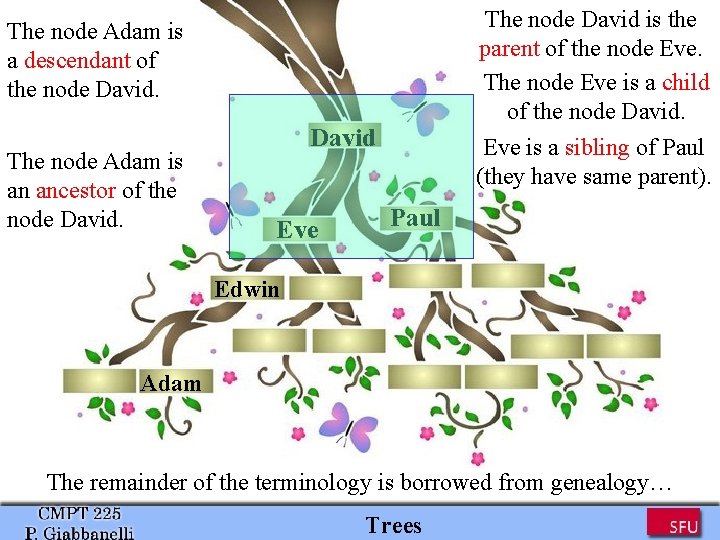
The node David is the parent of the node Eve. The node Eve is a child of the node David. Eve is a sibling of Paul (they have same parent). The node Adam is a descendant of the node David. The node Adam is an ancestor of the node David Eve Paul Edwin Adam The remainder of the terminology is borrowed from genealogy… Trees

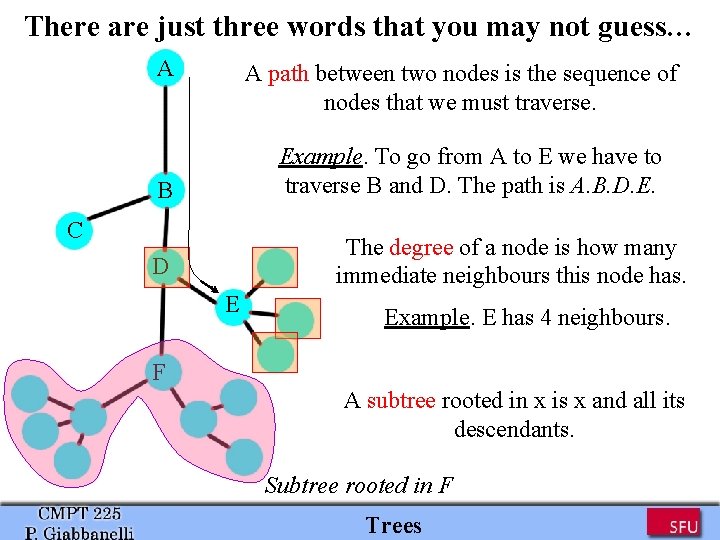
There are just three words that you may not guess… A A path between two nodes is the sequence of nodes that we must traverse. Example. To go from A to E we have to traverse B and D. The path is A. B. D. E. B C The degree of a node is how many immediate neighbours this node has. D E Example. E has 4 neighbours. F A subtree rooted in x is x and all its descendants. Subtree rooted in F Trees

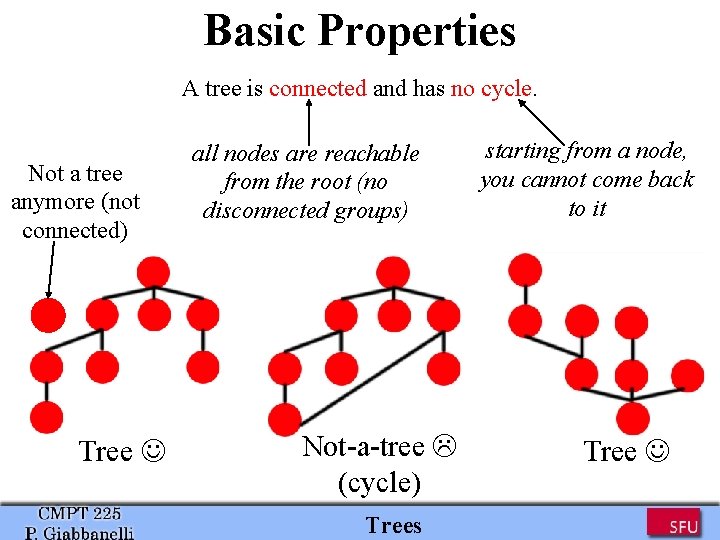
Basic Properties A tree is connected and has no cycle. Not a tree anymore (not connected) Tree all nodes are reachable from the root (no disconnected groups) Not-a-tree (cycle) Trees starting from a node, you cannot come back to it Tree

Pointer-based implementation It’s like a Linked. List but each instead of having only one neighbour next, a Node can have many neighbours. private class Node{ ? List<Node> neighbours; Object data; public Node(Object o){ data = o; If later I decide it’s wiser to have an Array. List, I don’t have to change much: I said I have a List, it is still one! ? neighbours = new Linked. List(); } } Trees

Pointer-based implementation It’s like a Linked. List but each instead of having only one neighbour next, a Node can have many neighbours. // we ignore Exceptions public Node get. Child(int i){ return neighbours. get(i); } public void add(Object o){ neighbours. add(new Node(o)); } public boolean has. Children(){ return !neighbours. is. Empty(); } public int get. Num. Children(){ return neighbours. size(); Trees }

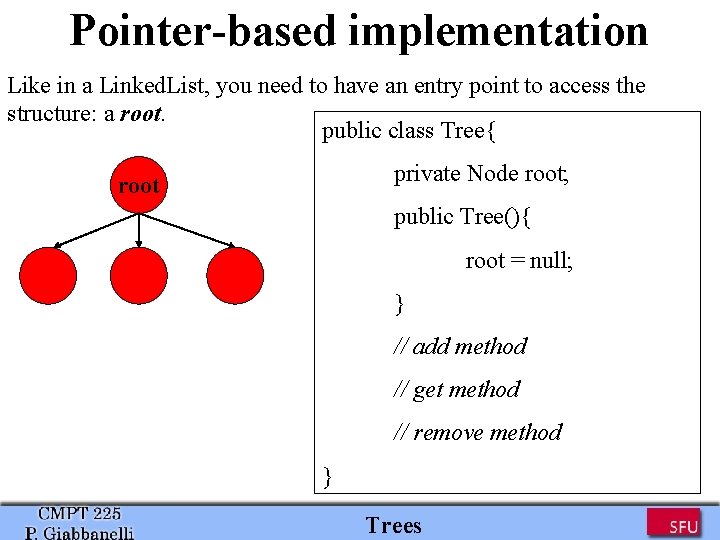
Pointer-based implementation Like in a Linked. List, you need to have an entry point to access the structure: a root. public class Tree{ private Node root; root public Tree(){ root = null; } // add method // get method // remove method } Trees

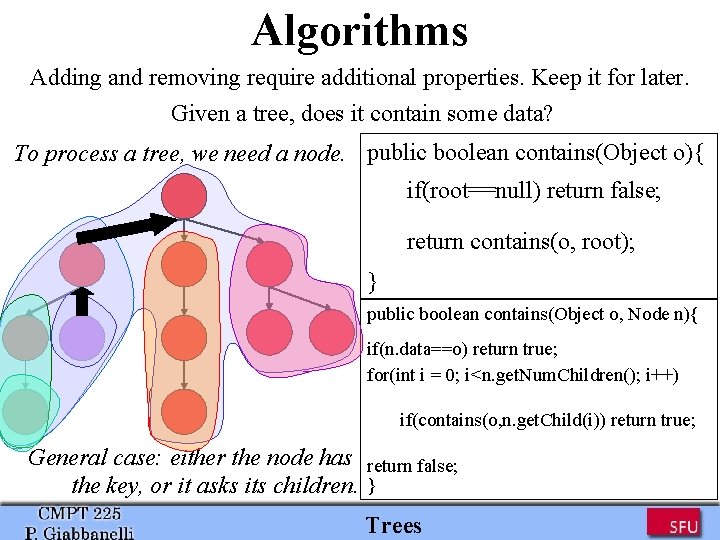
Algorithms Adding and removing require additional properties. Keep it for later. Given a tree, does it contain some data? To process a tree, we need a node. public boolean contains(Object o){ if(root==null) return false; return contains(o, root); } public boolean contains(Object o, Node n){ if(n. data==o) return true; for(int i = 0; i<n. get. Num. Children(); i++) if(contains(o, n. get. Child(i)) return true; General case: either the node has the key, or it asks its children. return false; } Trees

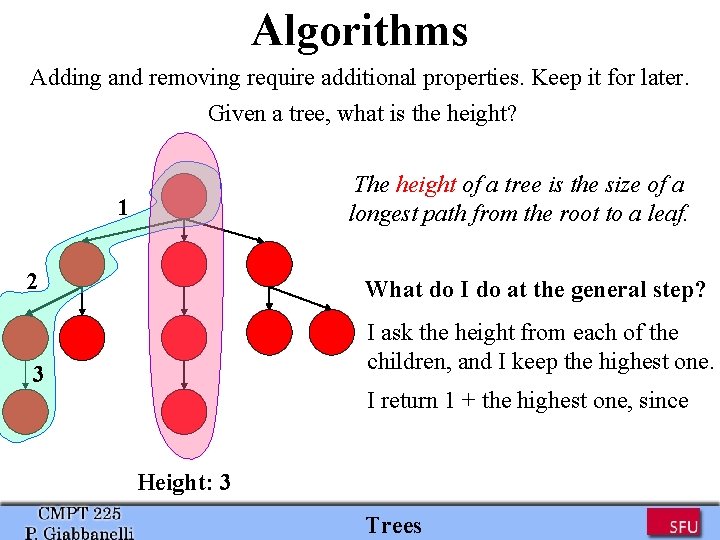
Algorithms Adding and removing require additional properties. Keep it for later. Given a tree, what is the height? The height of a tree is the size of a longest path from the root to a leaf. 1 2 What do I do at the general step? I ask the height from each of the children, and I keep the highest one. 3 I return 1 + the highest one, since Height: 3 Trees

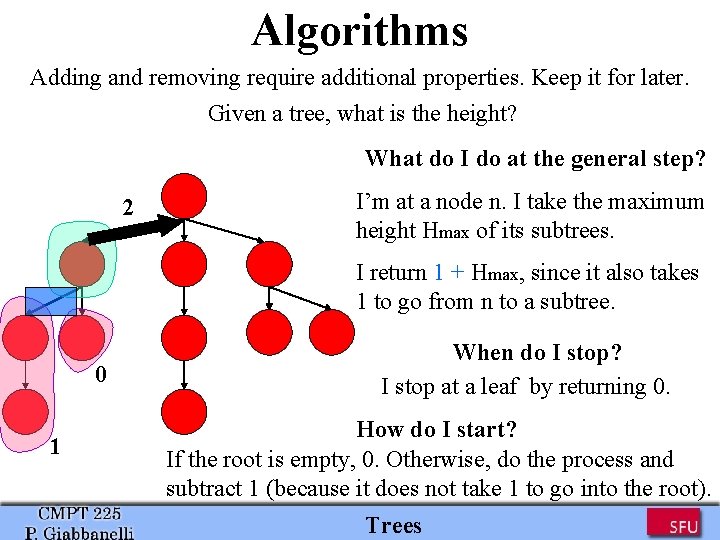
Algorithms Adding and removing require additional properties. Keep it for later. Given a tree, what is the height? What do I do at the general step? 2 I’m at a node n. I take the maximum height Hmax of its subtrees. I return 1 + Hmax, since it also takes 1 to go from n to a subtree. 0 1 When do I stop? I stop at a leaf by returning 0. How do I start? If the root is empty, 0. Otherwise, do the process and subtract 1 (because it does not take 1 to go into the root). Trees

Algorithms Adding and removing require additional properties. Keep it for later. Given a tree, what is the height? public int get. Height(){ if(root==null) return 0; return get. Height(root) – 1; } private int get. Height(Node n){ int max. Sub. Height = – 1; for(int i = 0; i<n. get. Num. Children; i++){ int curr. Height = get. Height(n. get. Child(i)); if(curr. Height>max. Sub. Height) max. Sub. Height = curr. Height; } return 1 + max. Sub. Height; } If there is no children then I return 1 – 1 = 0 as a leaf. Trees

Practice Time Return the number of nodes in the tree. Keywords to remember: get. Num. Children() Trees get. Child(i) root

Practice Time Return the number of nodes in the tree. What do I do at the general step? 1 + (1 + 2) I’m at a node n. I compute the total T of the number of nodes in the subtrees. I return T + 1 for myself (the node n). When do I stop? 1 2 I stop at a leaf by returning 1. How to I start? No root : 0. Otherwise, return the result starting from the root. Trees

Practice Time Return the number of nodes in the tree. public int get. Num. Nodes(){ if(root==null) return 0; return get. Num. Nodes(root); } private int get. Num. Nodes(Node n){ if(n==null) return 0; int total = 0; for(int i = 0; i<n. get. Num. Children(); i++) total += get. Num. Nodes(n. get. Child(i)); return 1 + total; } Trees

Practice Time Return the number of leaves in the tree. Keywords to remember: Start: no root? 0 leaves. A root? Return the result. Stop: leaf. Count 1. General step: return the sum of leaves in subtrees. get. Num. Children() get. Child(i) root public int get. Num. Leaves(){ if(root==null) return 0; return get. Num. Leaves(root); } private int get. Num. Leaves(Node n){ if(n. get. Number. Children()==0) return 1; int total = 0; for(int i = 0; i<n. get. Number. Children(); i++) total += get. Num. Leaves(n. get. Child(i)); return total; } Trees

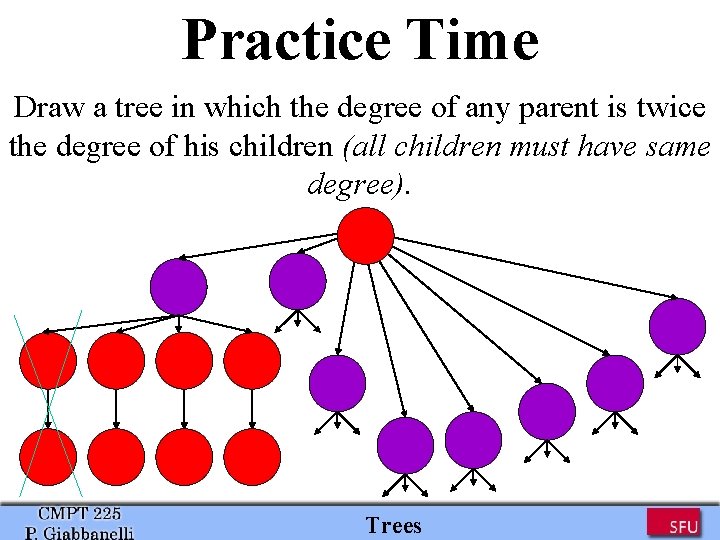
Practice Time Draw a tree in which the degree of any parent is twice the degree of his children (all children must have same degree). Trees

Algorithms We want to print the content of a tree (to. String)… There are many possible ways… Preorder? Show the node, then go to the children. Postorder? Show the children the node. Trees

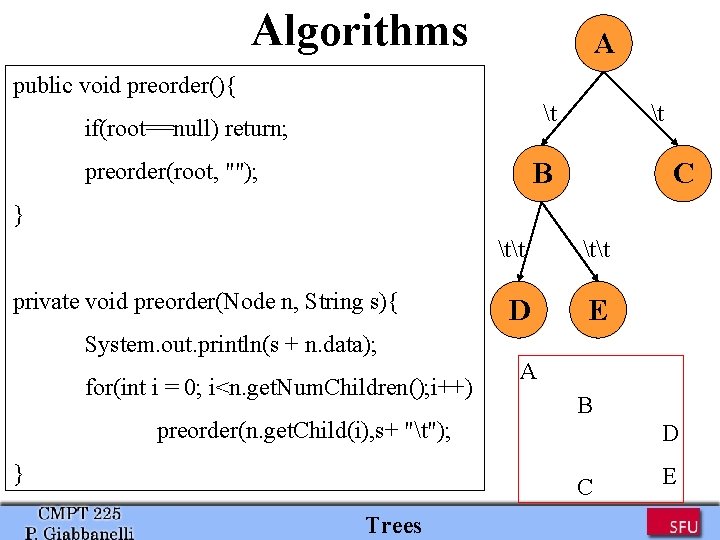
Algorithms A public void preorder(){ t if(root==null) return; t B preorder(root, ""); C } private void preorder(Node n, String s){ tt D E System. out. println(s + n. data); for(int i = 0; i<n. get. Num. Children(); i++) preorder(n. get. Child(i), s+ "t"); } A B D C Trees E

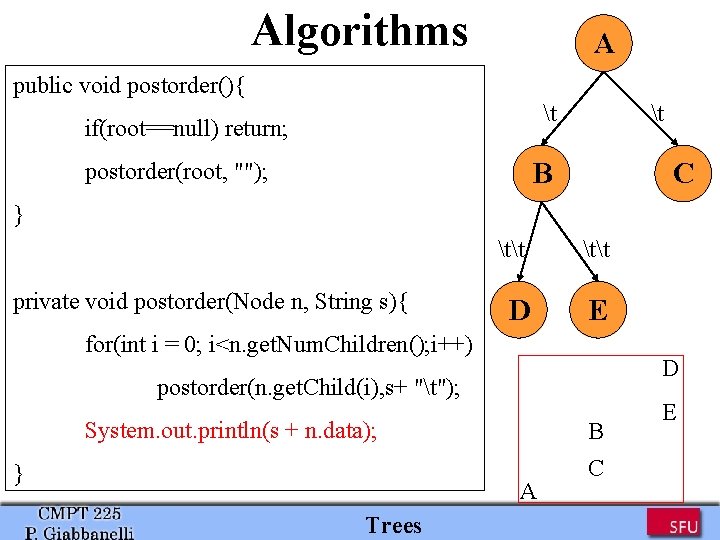
Algorithms A public void postorder(){ t if(root==null) return; t B postorder(root, ""); C } private void postorder(Node n, String s){ tt D E for(int i = 0; i<n. get. Num. Children(); i++) D postorder(n. get. Child(i), s+ "t"); System. out. println(s + n. data); } B A Trees C E

Some work for home (yeaaah ! ) Write a function that assigns to each node’s data the depth at which it is in the tree. For example, the root is at depth 0 so its data will be 0; its children are depth 1 so their data will be 1, etc. Write a function same that takes as argument a Tree and return false if it is different from the current tree, and true otherwise. Assume only integers in the tree. Write a function that adds all the integers, each one being multiplied by its depth in the tree.