Trees The definitions for this presentation are from

Trees The definitions for this presentation are from: Corman , et. al. , Introduction to Algorithms (MIT Press), Chapter 5. Some material on binomial trees is from Hull. Data Structures and Algorithms 1

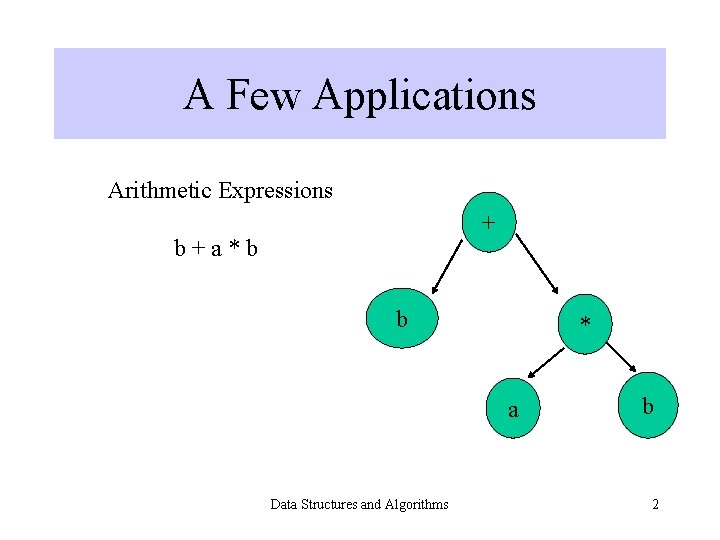
A Few Applications Arithmetic Expressions + b+a*b b * a Data Structures and Algorithms b 2

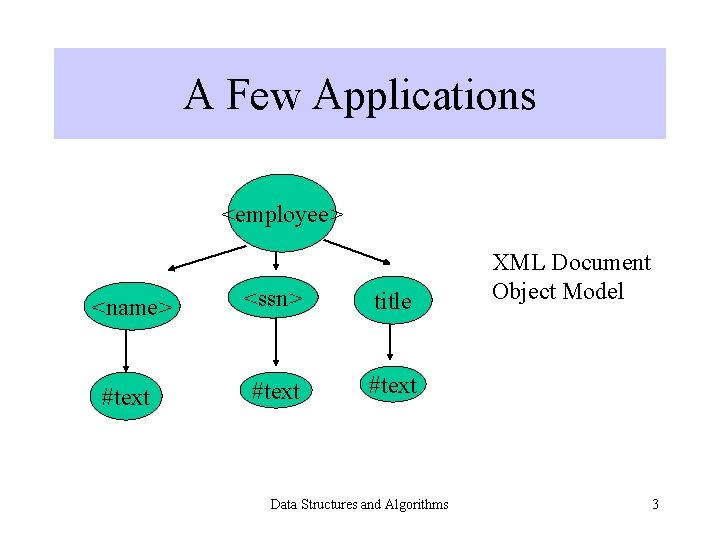
A Few Applications <employee> <name> <ssn> title #text Data Structures and Algorithms XML Document Object Model 3

A Few Applications Binomial “Trees” Movements Binomial trees are in Time dt frequently used to S p Su 1–p Sd From Hull approximate the movements in the price of a stock or other asset In each small interval of time the stock price is assumed to move up by a proportional amount u or to move down by a proportional amount d. 4

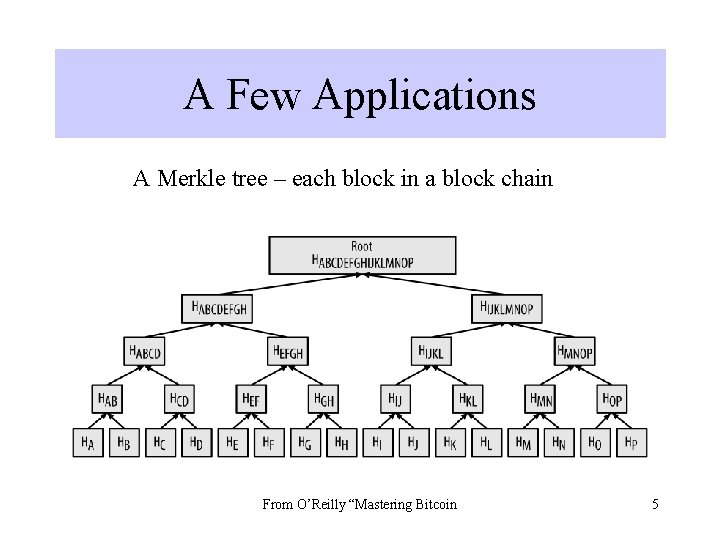
A Few Applications A Merkle tree – each block in a block chain From O’Reilly “Mastering Bitcoin 5

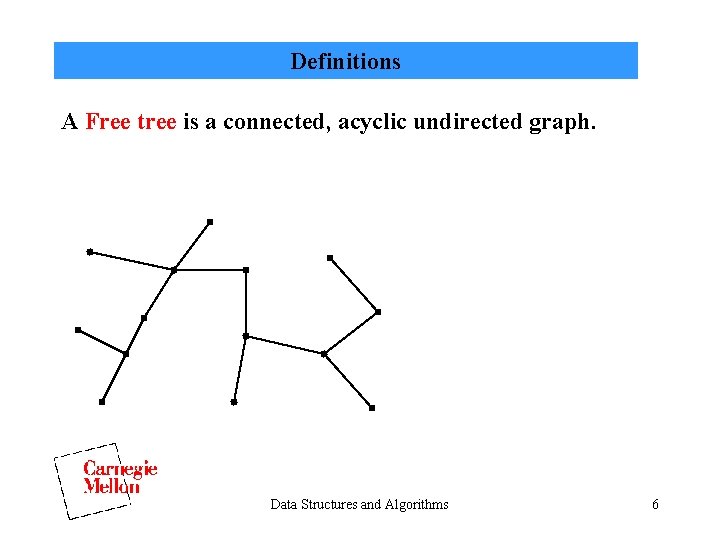
Definitions A Free tree is a connected, acyclic undirected graph. Data Structures and Algorithms 6

If an undirected graph is acyclic but possibly disconnected, it is a forest. Data Structures and Algorithms 7

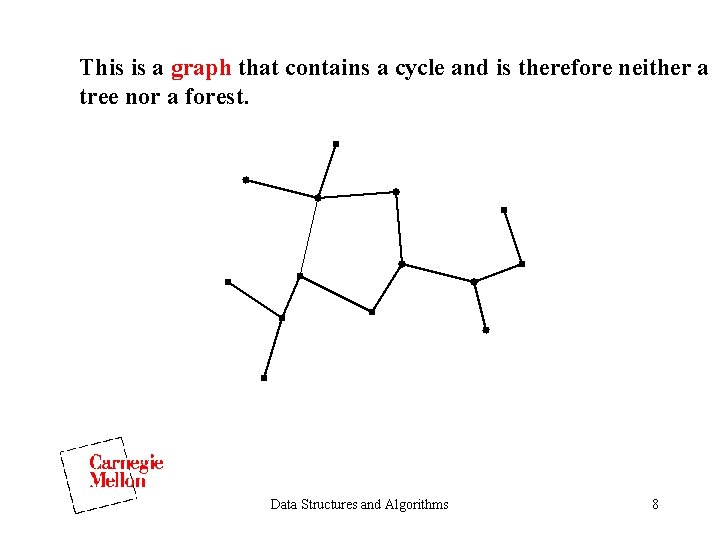
This is a graph that contains a cycle and is therefore neither a tree nor a forest. Data Structures and Algorithms 8

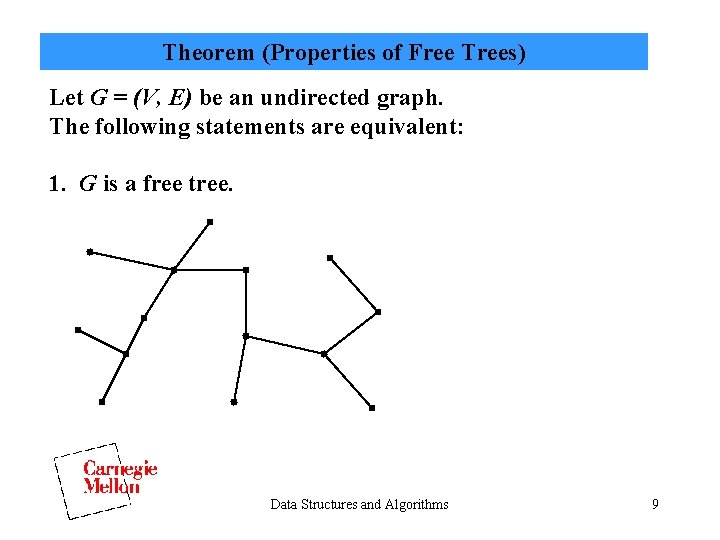
Theorem (Properties of Free Trees) Let G = (V, E) be an undirected graph. The following statements are equivalent: 1. G is a free tree. Data Structures and Algorithms 9

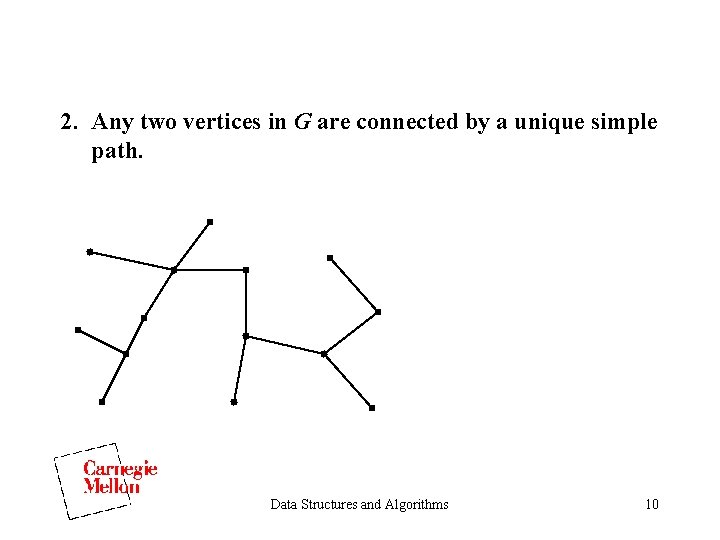
2. Any two vertices in G are connected by a unique simple path. Data Structures and Algorithms 10

3. G is connected, but if any edge is removed from E, the resulting graph is disconnected. Data Structures and Algorithms 11

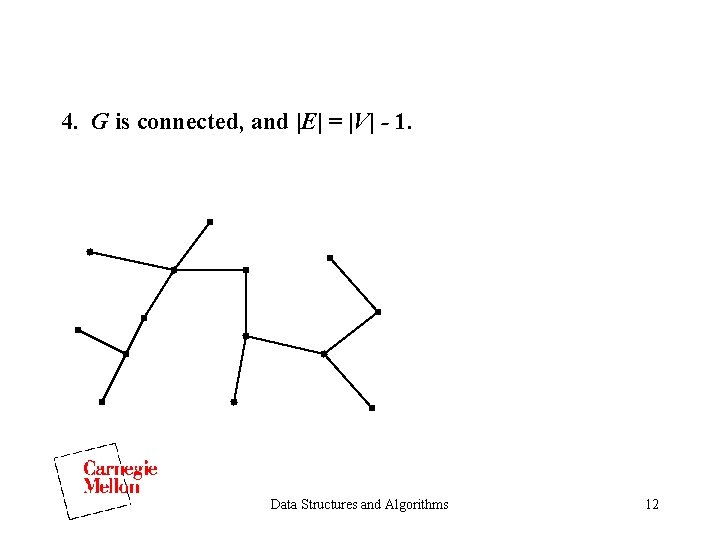
4. G is connected, and |E| = |V| - 1. Data Structures and Algorithms 12

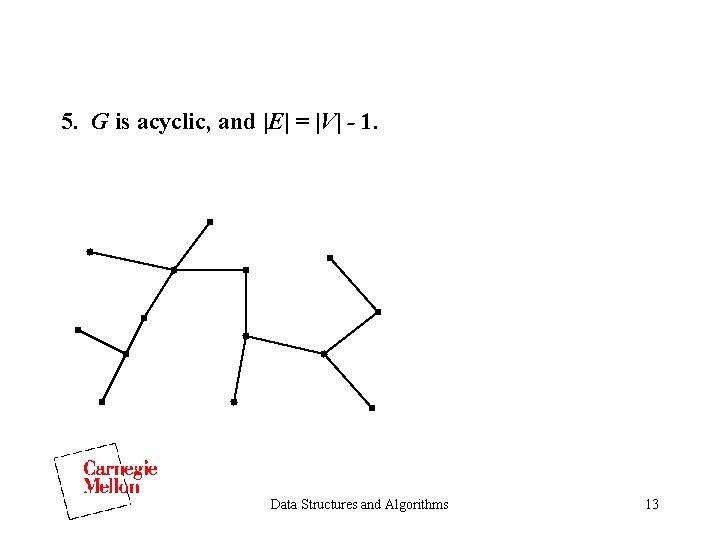
5. G is acyclic, and |E| = |V| - 1. Data Structures and Algorithms 13

6. G is acyclic, but if any edge is added to E, the resulting graph contains a cycle. Data Structures and Algorithms 14

A rooted tree is a free tree in which one of the vertices is distinguished from the others. The distinguished vertex is called the root of the tree. We often refer to a vertex of a rooted tree as a node (we may also call this a vertex) of the tree. The following figure shows a rooted tree on a set of 12 nodes with root 7. 7 3 8 6 10 12 5 4 11 2 1 9 Data Structures and Algorithms 15

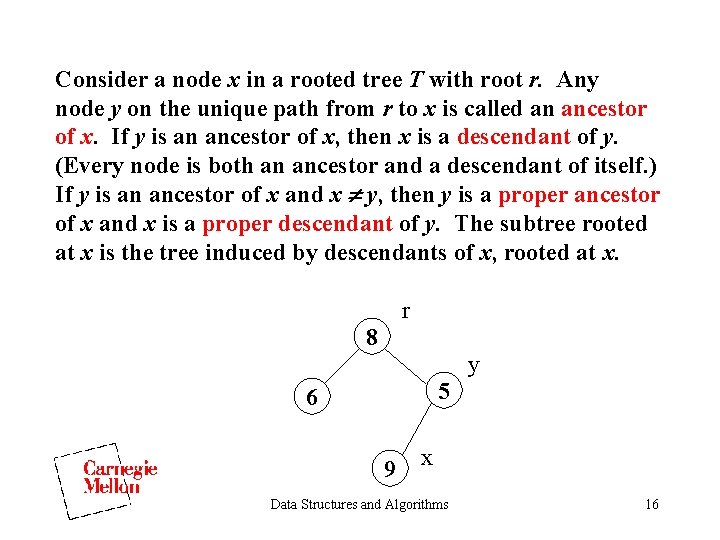
Consider a node x in a rooted tree T with root r. Any node y on the unique path from r to x is called an ancestor of x. If y is an ancestor of x, then x is a descendant of y. (Every node is both an ancestor and a descendant of itself. ) If y is an ancestor of x and x y, then y is a proper ancestor of x and x is a proper descendant of y. The subtree rooted at x is the tree induced by descendants of x, rooted at x. r 8 y 5 6 9 x Data Structures and Algorithms 16

If the last edge on the path from the root r of a tree T to a node x is (y, x), then y is the parent of x, and x is a child of y. The root is the only node in T with no parent. If two nodes have the same parent, they are siblings. A node with no children is an external node or leaf. A nonleaf node is an internal node. Data Structures and Algorithms 17

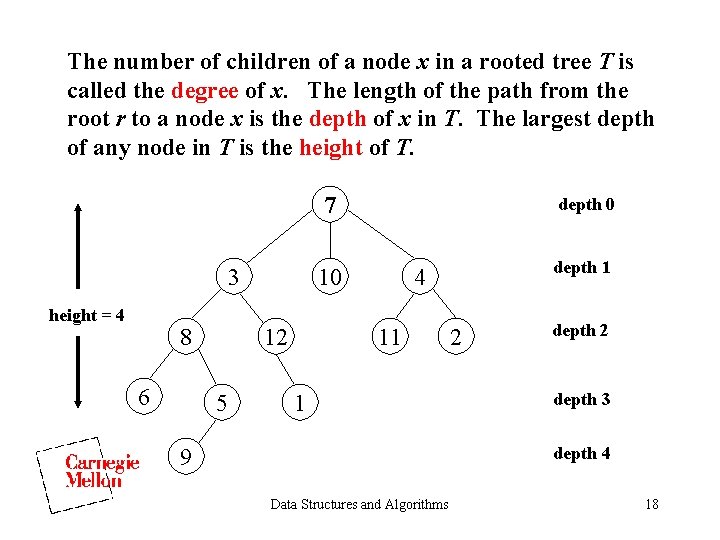
The number of children of a node x in a rooted tree T is called the degree of x. The length of the path from the root r to a node x is the depth of x in T. The largest depth of any node in T is the height of T. 7 3 height = 4 8 6 10 12 5 depth 0 depth 1 4 11 1 2 depth 3 depth 4 9 Data Structures and Algorithms 18

An ordered tree is a rooted tree in which the children of each node are ordered. That is, if a node has k children, then there is a first child, a second child, …, and a kth child. The two trees shown below are different when considered to be ordered trees, but the same when considered to be just rooted trees. 7 7 3 8 6 11 12 5 4 10 1 3 12 2 1 9 10 8 6 4 11 2 5 9 Data Structures and Algorithms 19

A binary tree T is a structure defined on a finite set of nodes that either • contains no nodes, or • is comprised of three disjoint sets of nodes: a root node, a binary tree called its left subtree and a binary tree called its right subtree. 3 2 4 1 7 5 6 Data Structures and Algorithms 20

Full binary tree: each node is either a leaf or has degree exactly 2. In a positional tree, the children of a node are labeled with distinct positive integers. The ith child of a node is absent if no child is labeled with integer i. A k-ary tree is a positional tree in which for every node, all children with labels greater than k are missing. Thus, a binary tree is a k-ary tree with k = 2. Data Structures and Algorithms 21

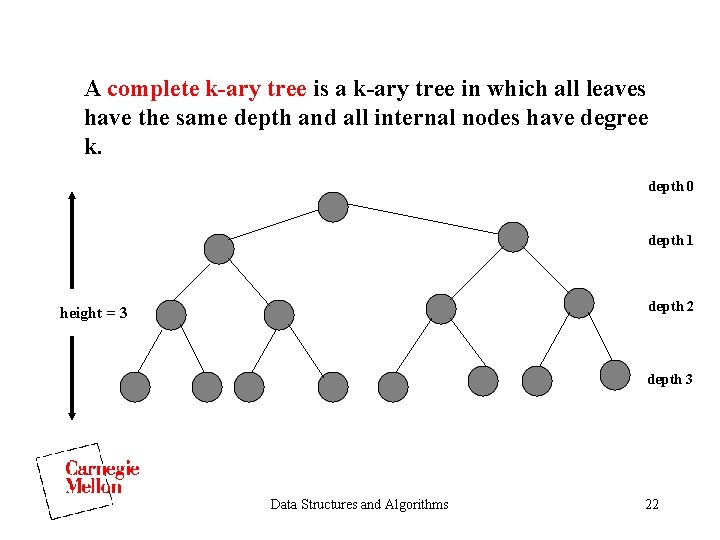
A complete k-ary tree is a k-ary tree in which all leaves have the same depth and all internal nodes have degree k. depth 0 depth 1 depth 2 height = 3 depth 3 Data Structures and Algorithms 22

How many leaves L does a complete binary tree of height h have? d=0 d= 1 d=2 The number of leaves at depth d = 2 d If the height of the tree is h it has 2 h leaves. L = 2 h. Data Structures and Algorithms 23

What is the height h of a complete binary tree with L leaves? leaves = 1 height = 0 leaves = 2 height = 1 leaves = 4 height = 2 leaves = L height = Log 2 L Since L = 2 h Log 2 L = Log 22 h h = Log 2 L Data Structures and Algorithms 24

The number of internal nodes of a complete binary tree of height h is ? 1 + 22 +. . . + 2 h-1 = 2 i Internal nodes = 0 height = 0 Internal nodes = 1 height = 1 Internal nodes = 1 + 2 height = 2 Internal nodes = 1 + 2 + 4 height = 3 Geometric series = 2 h - 1 2 -1 Thus, a complete binary tree of height = h has 2 h-1 internal nodes. Data Structures and Algorithms 25

The number of nodes n of a complete binary tree of height h is ? nodes = 1 height = 0 nodes = 3 height = 1 nodes = 7 height = 2 nodes = 2 h+1 - 1 height = h Since L = 2 h and since the number of internal nodes = 2 h-1 the total number of nodes n = 2 h+ 2 h-1 = 2(2 h) – 1 = 2 h+1 - 1. Data Structures and Algorithms 26

If the number of nodes is n then what is the height? nodes = 1 height = 0 nodes = 3 height = 1 nodes = 7 height = 2 nodes = n height = Log 2(n+1) - 1 Since n = 2 h+1 -1 n + 1 = 2 h+1 Log 2(n+1) = Log 2 2 h+1 Log 2(n+1) = h+1 h = Log 2(n+1) - 1 Data Structures and Algorithms 27

Catalan Numbers = 1 (2 n)! (n+1) n! (2 n-n)! 1, 1, 2, 5, 14, . . . Data Structures and Algorithms 28

The number of distinct binary trees with n nodes N=0 N=1 N=3 N=2 . . . Data Structures and Algorithms 29

Class for Binary Nodes public class BTNode { private Object data; private BTNode left; private BTNode right; . . . Data Structures and Algorithms 30

public BTNode(Object obj, BTNode l, BTNode r) { data = obj; left = l; right= r; } public boolean is. Leaf() { return (left == null) && (right == null); }. . . Data Structures and Algorithms 31

Copying Trees public static BTNode tree. Copy(BTNode t) { if (t == null) return null; else { BTNode left. Copy = tree. Copy(t. left); BTNode right. Copy = tree. Copy(t. right); return new BTNode(t. data, left. Copy, right. Cop y); } Data Structures and Algorithms 32

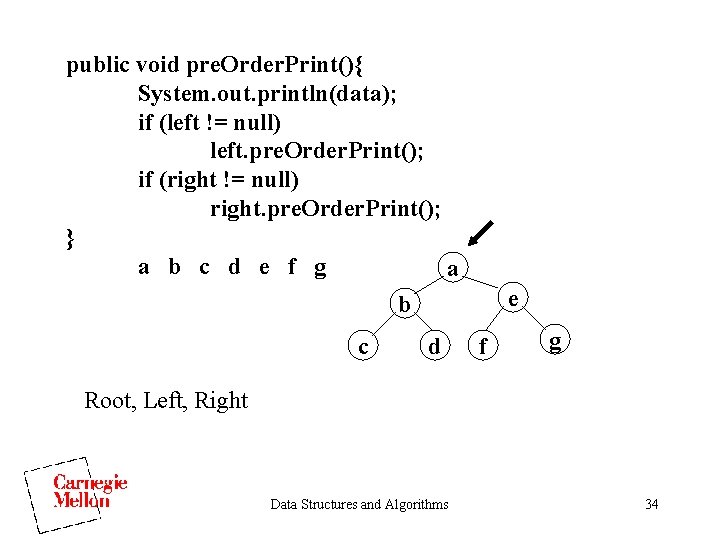
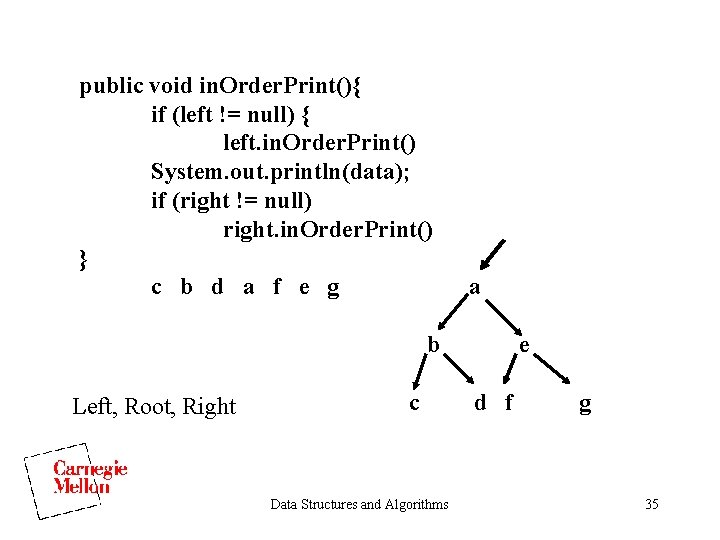
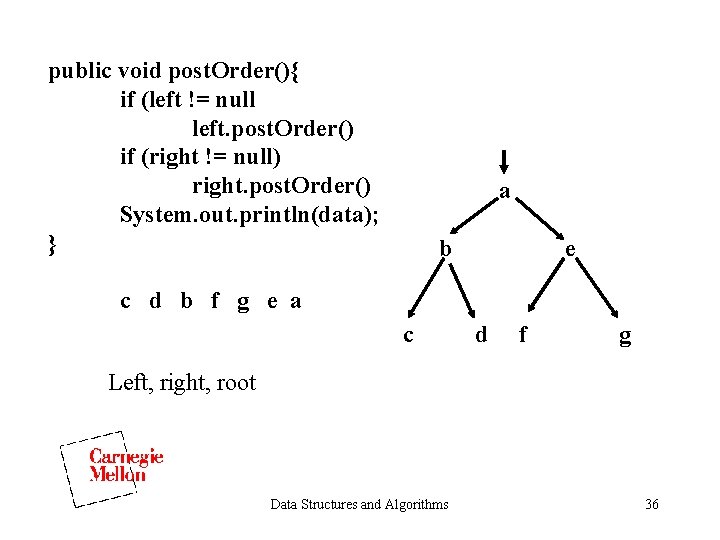
Tree Traversals • Preorder • Inorder • Postorder • Levelorder Data Structures and Algorithms 33

public void pre. Order. Print(){ System. out. println(data); if (left != null) left. pre. Order. Print(); if (right != null) right. pre. Order. Print(); } a b c d e f g a e b c d f g Root, Left, Right Data Structures and Algorithms 34

public void in. Order. Print(){ if (left != null) { left. in. Order. Print() System. out. println(data); if (right != null) right. in. Order. Print() } c b d a f e g a b Left, Root, Right c Data Structures and Algorithms e d f g 35

public void post. Order(){ if (left != null left. post. Order() if (right != null) right. post. Order() System. out. println(data); } a b e c d b f g e a c d f g Left, right, root Data Structures and Algorithms 36

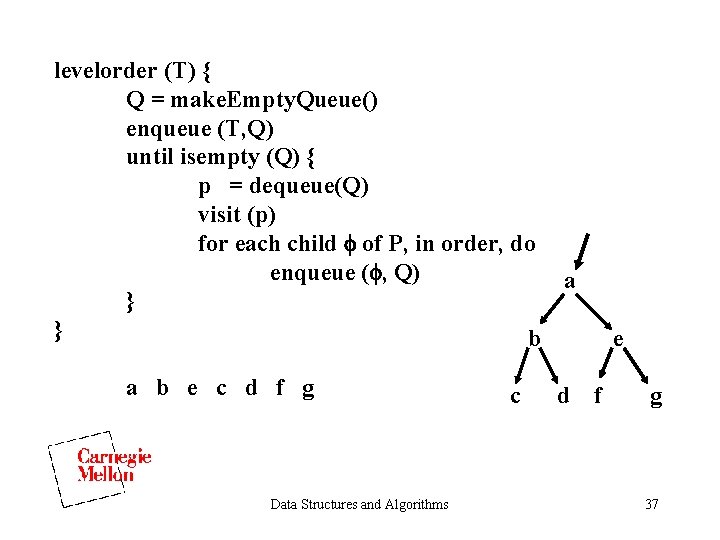
levelorder (T) { Q = make. Empty. Queue() enqueue (T, Q) until isempty (Q) { p = dequeue(Q) visit (p) for each child of P, in order, do enqueue ( , Q) a } } b a b e c d f g Data Structures and Algorithms c d e f g 37

An Array Representation Suppose we are lucky enough to be working with complete binary trees. We can store the tree in an array. Let the root be at index 0 and let the left and right children of node i be at indexes 2 i+1 and 2 i+2 respectively. Lewis and Denemberg, Page 111 Data Structures and Algorithms 38

An Array Representation is. Leaf(i) : 2 i + 1 >= n left. Child(i) : 2 i + 1 (none if 2 i+ 1 >= n) right. Child(i): 2 i + 2 (none if 2 i + 2 >= n) left. Sibling(i): i - 1 (none if i == 0 or i is odd) right. Sibling(i) : i + 1 (none if i = n-1 or i is even) parent(i) = int((i-1)/2) (none if i == 0) Works if the tree is “almost complete”, growing top to bottom and left to right. Lewis and Denemberg, Page 111 Data Structures and Algorithms 39

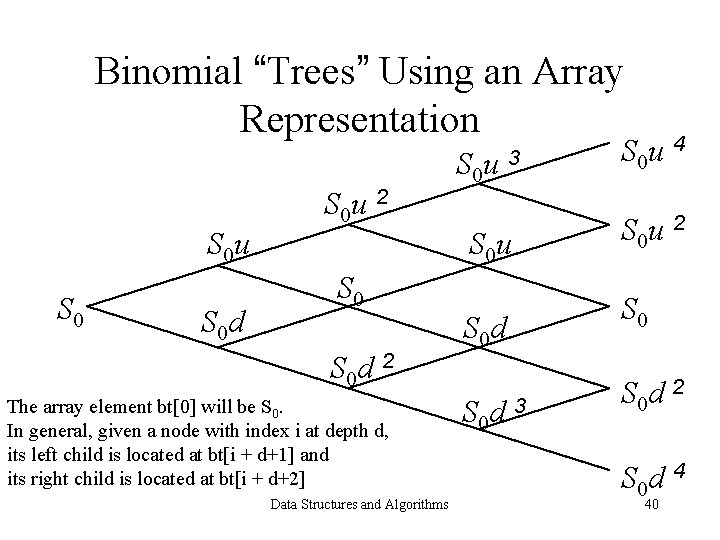
Binomial “Trees” Using an Array Representation S 0 u S 0 d S 0 u 2 S 0 d 2 The array element bt[0] will be S 0. In general, given a node with index i at depth d, its left child is located at bt[i + d+1] and its right child is located at bt[i + d+2] Data Structures and Algorithms S 0 u 3 S 0 u 4 S 0 u 2 S 0 d 3 S 0 d 2 S 0 d 4 40